18.1.2 从一组对边的角度判定平行四边形 练习题 2021——2022学年人教版八年级数学下册(word版含解析)
文档属性
| 名称 | 18.1.2 从一组对边的角度判定平行四边形 练习题 2021——2022学年人教版八年级数学下册(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 08:14:24 | ||
图片预览


文档简介
18.1.2第2课时
从一组对边的角度判定平行四边形
一、选择题
1.下列条件中,不能判定四边形是平行四边形的是 ( )
A.两组对边分别相等的四边形 B.两组对角分别相等的四边形
C.一组对边平行且相等的四边形 D.一组对边平行且另一组对边相等的四边形
2.在四边形ABCD中,①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从以上条件中选择两个条件,使四边形ABCD为平行四边形的选法共有 ( )
A.3种 B.4种 C.5种 D.6种
3.如图1所示,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF,添加一个条件,使四边形ABCD是平行四边形,你认为下面四个条件中可以选择的是 ( )
图1
A.AD=BC B.CD=BF C.∠A=∠C D.∠F=∠CDE
4.八年级(6)班的一个互助学习小组组长收集并整理了组员们讨论如下问题时写出的条件.
如图2所示,在四边形ABCD中,点E,F分别在边BC,AD上.
图2
求证:四边形AECF是平行四边形.
你能写出最少且简捷的条件使结论成立吗
条件分别是:①BE=DF;②∠B=∠D;③∠BAE=∠DCF;④四边形ABCD是平行四边形.
下面是A,B,C,D四位同学所填条件,其中符合题目要求的是 ( )
A.①②③④ B.①②③ C.①④ D.④
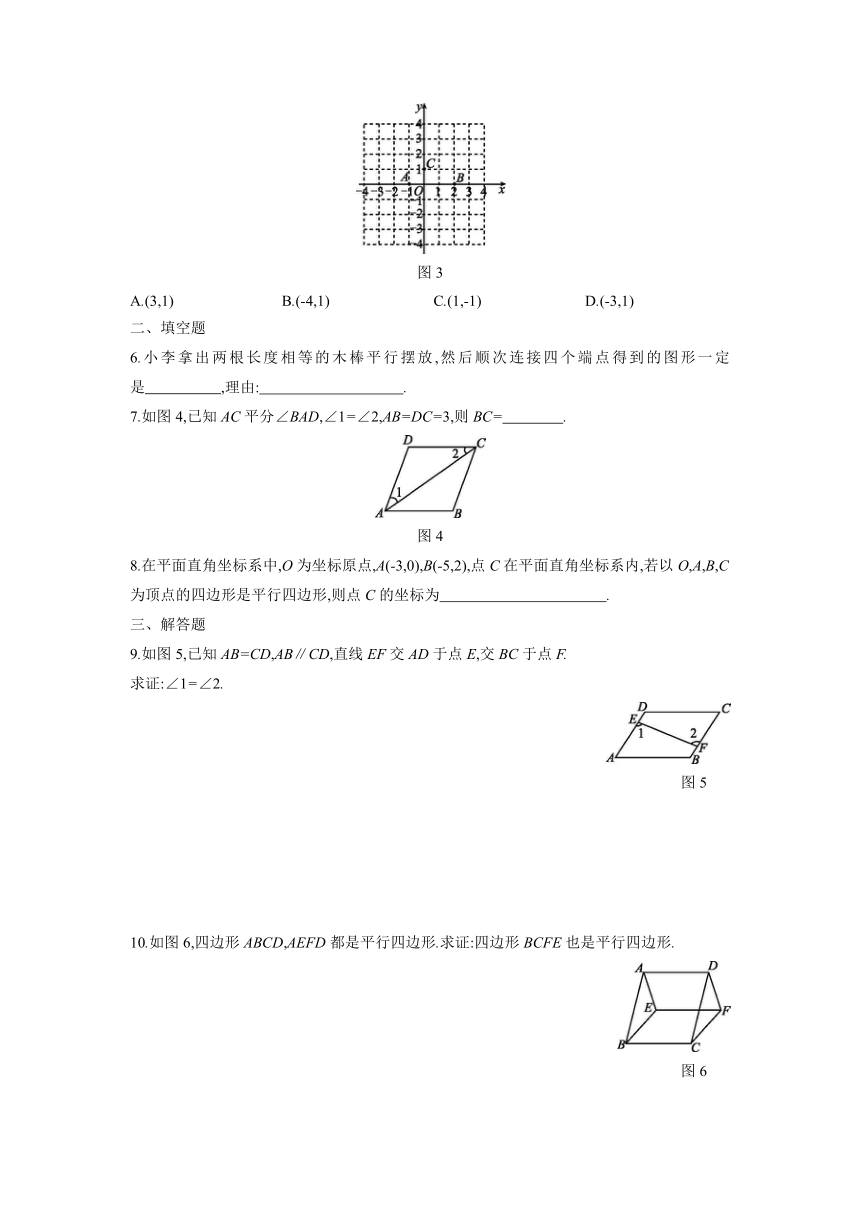
5.如图3,在平面直角坐标系中,以点A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形第四个顶点的是( )
图3
A.(3,1) B.(-4,1) C.(1,-1) D.(-3,1)
二、填空题
6.小李拿出两根长度相等的木棒平行摆放,然后顺次连接四个端点得到的图形一定是 ,理由: .
7.如图4,已知AC平分∠BAD,∠1=∠2,AB=DC=3,则BC= .
图4
8.在平面直角坐标系中,O为坐标原点,A(-3,0),B(-5,2),点C在平面直角坐标系内,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为 .
三、解答题
9.如图5,已知AB=CD,AB∥CD,直线EF交AD于点E,交BC于点F.
求证:∠1=∠2.
图5
10.如图6,四边形ABCD,AEFD都是平行四边形.求证:四边形BCFE也是平行四边形.
图6
11.如图7,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,AE=CF.求证:四边形ABCD是平行四边形.
图7
12.如图8,在 ABCD中,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE.
求证:AF=CE.
图8
13.如图9,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AF=CE,DF∥BE.求证:四边形ABCD为平行四边形.
图9
14.如图10所示,在四边形ABCD中,AD∥BC,AD=24 cm,BC=30 cm.点P从点A开始向终点D以1 cm/s的速度匀速运动;点Q从点C开始向终点B以2 cm/s的速度匀速运动.两点同时出发,当其中一点到达终点时,另一点也随之停止运动.直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点出发几秒后,所截得的两个四边形中,其中一个四边形为平行四边形
图10
答案
1.D
2.B [解析] 根据平行四边形的判定,符合条件的有4种,分别是:①②、②④、①③、③④.
3.D [解析] 若选择∠F=∠CDE,则CD∥BF.
又因为BE=CE,∠BEF=∠CED,
所以△BEF≌△CED(AAS),所以CD=BF.
又因为AB=BF,
所以CD=AB.
又因为CD∥AB,
所以四边形ABCD是平行四边形.
4.C [解析] 当添加条件①④时,可得四边形AECF是平行四边形.
理由如下:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵BE=DF,
∴AD-DF=BC-BE,即AF=EC.
又∵AF∥CE,
∴四边形AECF是平行四边形.
5.B [解析] 如图所示:
①以AC为对角线,可以画出 AFCB,F(-3,1);
②以AB为对角线,可以画出 ACBE,E(1,-1);
③以BC为对角线,可以画出 ACDB,D(3,1).
故选B.
6.平行四边形 一组对边平行且相等的四边形是平行四边形
7.3
8.(-2,2)或(-8,2)或(2,-2)
[解析] 如图所示.
∵A(-3,0),
∴OA=3.
①当四边形OABC是平行四边形时,BC=OA=3.
∵B(-5,2),
∴C(-2,2);
②当四边形OAC'B是平行四边形时,BC'=OA=3.
∵B(-5,2),
∴C'(-8,2);
③当四边形OBAC″是平行四边形时,
∵A(-3,0),B(-5,2),O(0,0),
∴C″(2,-2).
故答案为(-2,2)或(-8,2)或(2,-2).
9.证明:∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,∴∠1=∠2.
10.证明:∵四边形ABCD,AEFD都是平行四边形,
∴AD∥BC,AD=BC,AD∥EF,AD=EF,
∴BC∥EF,BC=EF,
∴四边形BCFE也是平行四边形.
11.证明:∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°.
∵AD∥BC,∴∠ADE=∠CBF.
又∵AE=CF,
∴△AED≌△CFB(AAS),
∴AD=BC.
又∵AD∥BC,
∴四边形ABCD是平行四边形.
12.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∴∠ADB=∠CBD.
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB,AE∥CF,
∴△AED≌△CFB,∴AE=CF,
∴四边形AECF是平行四边形,∴AF=CE.
13.证明:∵AB∥CD,
∴∠DCA=∠BAC.
∵DF∥BE,∴∠DFA=∠BEC,
∴∠CFD=∠AEB.
∵AF=CE,
∴AF-EF=CE-EF,即AE=CF.
在△AEB和△CFD中,
∴△AEB≌△CFD(ASA),
∴AB=CD.
又∵AB∥CD,
∴四边形ABCD为平行四边形.
14.解:设运动时间为t s.根据题意,得AP=t cm,PD=(24-t)cm,CQ=2t cm,BQ=(30-2t)cm.
①若四边形ABQP是平行四边形,
∵AD∥BC,∴还需满足AP=BQ,
∴t=30-2t,解得t=10,
∴当P,Q两点出发10 s后,四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,
∵AD∥BC,∴还需满足PD=CQ,
∴24-t=2t,解得t=8,
∴当P,Q两点出发8 s后,四边形PQCD是平行四边形.
综上所述,当P,Q两点出发8 s或10 s后,所截得的两个四边形中,其中一个四边形为平行四边形.
从一组对边的角度判定平行四边形
一、选择题
1.下列条件中,不能判定四边形是平行四边形的是 ( )
A.两组对边分别相等的四边形 B.两组对角分别相等的四边形
C.一组对边平行且相等的四边形 D.一组对边平行且另一组对边相等的四边形
2.在四边形ABCD中,①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从以上条件中选择两个条件,使四边形ABCD为平行四边形的选法共有 ( )
A.3种 B.4种 C.5种 D.6种
3.如图1所示,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF,添加一个条件,使四边形ABCD是平行四边形,你认为下面四个条件中可以选择的是 ( )
图1
A.AD=BC B.CD=BF C.∠A=∠C D.∠F=∠CDE
4.八年级(6)班的一个互助学习小组组长收集并整理了组员们讨论如下问题时写出的条件.
如图2所示,在四边形ABCD中,点E,F分别在边BC,AD上.
图2
求证:四边形AECF是平行四边形.
你能写出最少且简捷的条件使结论成立吗
条件分别是:①BE=DF;②∠B=∠D;③∠BAE=∠DCF;④四边形ABCD是平行四边形.
下面是A,B,C,D四位同学所填条件,其中符合题目要求的是 ( )
A.①②③④ B.①②③ C.①④ D.④
5.如图3,在平面直角坐标系中,以点A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形第四个顶点的是( )
图3
A.(3,1) B.(-4,1) C.(1,-1) D.(-3,1)
二、填空题
6.小李拿出两根长度相等的木棒平行摆放,然后顺次连接四个端点得到的图形一定是 ,理由: .
7.如图4,已知AC平分∠BAD,∠1=∠2,AB=DC=3,则BC= .
图4
8.在平面直角坐标系中,O为坐标原点,A(-3,0),B(-5,2),点C在平面直角坐标系内,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为 .
三、解答题
9.如图5,已知AB=CD,AB∥CD,直线EF交AD于点E,交BC于点F.
求证:∠1=∠2.
图5
10.如图6,四边形ABCD,AEFD都是平行四边形.求证:四边形BCFE也是平行四边形.
图6
11.如图7,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,AE=CF.求证:四边形ABCD是平行四边形.
图7
12.如图8,在 ABCD中,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE.
求证:AF=CE.
图8
13.如图9,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AF=CE,DF∥BE.求证:四边形ABCD为平行四边形.
图9
14.如图10所示,在四边形ABCD中,AD∥BC,AD=24 cm,BC=30 cm.点P从点A开始向终点D以1 cm/s的速度匀速运动;点Q从点C开始向终点B以2 cm/s的速度匀速运动.两点同时出发,当其中一点到达终点时,另一点也随之停止运动.直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点出发几秒后,所截得的两个四边形中,其中一个四边形为平行四边形
图10
答案
1.D
2.B [解析] 根据平行四边形的判定,符合条件的有4种,分别是:①②、②④、①③、③④.
3.D [解析] 若选择∠F=∠CDE,则CD∥BF.
又因为BE=CE,∠BEF=∠CED,
所以△BEF≌△CED(AAS),所以CD=BF.
又因为AB=BF,
所以CD=AB.
又因为CD∥AB,
所以四边形ABCD是平行四边形.
4.C [解析] 当添加条件①④时,可得四边形AECF是平行四边形.
理由如下:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵BE=DF,
∴AD-DF=BC-BE,即AF=EC.
又∵AF∥CE,
∴四边形AECF是平行四边形.
5.B [解析] 如图所示:
①以AC为对角线,可以画出 AFCB,F(-3,1);
②以AB为对角线,可以画出 ACBE,E(1,-1);
③以BC为对角线,可以画出 ACDB,D(3,1).
故选B.
6.平行四边形 一组对边平行且相等的四边形是平行四边形
7.3
8.(-2,2)或(-8,2)或(2,-2)
[解析] 如图所示.
∵A(-3,0),
∴OA=3.
①当四边形OABC是平行四边形时,BC=OA=3.
∵B(-5,2),
∴C(-2,2);
②当四边形OAC'B是平行四边形时,BC'=OA=3.
∵B(-5,2),
∴C'(-8,2);
③当四边形OBAC″是平行四边形时,
∵A(-3,0),B(-5,2),O(0,0),
∴C″(2,-2).
故答案为(-2,2)或(-8,2)或(2,-2).
9.证明:∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,∴∠1=∠2.
10.证明:∵四边形ABCD,AEFD都是平行四边形,
∴AD∥BC,AD=BC,AD∥EF,AD=EF,
∴BC∥EF,BC=EF,
∴四边形BCFE也是平行四边形.
11.证明:∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°.
∵AD∥BC,∴∠ADE=∠CBF.
又∵AE=CF,
∴△AED≌△CFB(AAS),
∴AD=BC.
又∵AD∥BC,
∴四边形ABCD是平行四边形.
12.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∴∠ADB=∠CBD.
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB,AE∥CF,
∴△AED≌△CFB,∴AE=CF,
∴四边形AECF是平行四边形,∴AF=CE.
13.证明:∵AB∥CD,
∴∠DCA=∠BAC.
∵DF∥BE,∴∠DFA=∠BEC,
∴∠CFD=∠AEB.
∵AF=CE,
∴AF-EF=CE-EF,即AE=CF.
在△AEB和△CFD中,
∴△AEB≌△CFD(ASA),
∴AB=CD.
又∵AB∥CD,
∴四边形ABCD为平行四边形.
14.解:设运动时间为t s.根据题意,得AP=t cm,PD=(24-t)cm,CQ=2t cm,BQ=(30-2t)cm.
①若四边形ABQP是平行四边形,
∵AD∥BC,∴还需满足AP=BQ,
∴t=30-2t,解得t=10,
∴当P,Q两点出发10 s后,四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,
∵AD∥BC,∴还需满足PD=CQ,
∴24-t=2t,解得t=8,
∴当P,Q两点出发8 s后,四边形PQCD是平行四边形.
综上所述,当P,Q两点出发8 s或10 s后,所截得的两个四边形中,其中一个四边形为平行四边形.
