人教版 五年级数学下册 第2单元第5课时 质数和合数 课件(共21张PPT)
文档属性
| 名称 | 人教版 五年级数学下册 第2单元第5课时 质数和合数 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 31.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 16:35:54 | ||
图片预览







文档简介
(共21张PPT)
质数和合数
人教版 五年级下册
学习目标
质数、合数和奇数、偶数的区别。
知道100以内的质数,熟悉20以内的质数。
理解质数和合数的概念,知道它们之间的联系。能正确判断一个数是质数还是合数。
情境导入
想一想:因数的特征是什么?
2的因数有( )
1、2
1、3、5、15
一个数的因数的个数是有限的,最小的因数都是1,最大的因数是本身。
15的因数有( )
情境导入
自然数 1-20 中,奇数有哪些?偶数有哪些?
你知道它们是按什么标准分类的吗?
奇数:1,3,5,7,9,11,13,15,17,19。
偶数:2,4,6,8,10,12,14,16,18,20。
情境导入
找出1~20各数的因数,看看他们的因数个数有什么规律。
怎么找一个数的因数呢?
找一个数的因数从最小因数找起,一直找到它本身,哪两个数相乘的积等于这个数,那么这两个数就是这个数的因数。
新课讲解
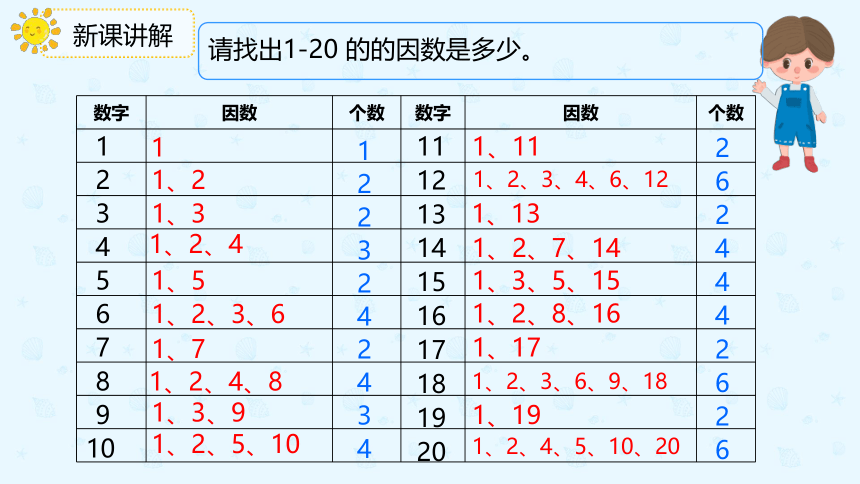
请找出1-20 的的因数是多少。
数字 因数 个数 数字 因数 个数
1
1、2
1、3
1、2、4
1、5
1、2、3、6
1、7
1、2、4、8
1、3、9
1、2、5、10
1、11
1、2、3、4、6、12
1、13
1、2、7、14
1、3、5、15
1、2、8、16
1、17
1、2、3、6、9、18
1、19
1、2、4、5、10、20
1
2
2
3
2
4
2
4
3
4
2
6
2
4
4
4
2
6
2
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
新课讲解
只有一个因数 只有1和它本身两个因数 有两个以上的因数
1
2,3,5,7,11,13,17,19……
4,6,8,9,10,12,14,15,16,18,20……
有的数只有两个因数,如5的因数是1和5。
1只有一个因数1。
有的数的因数不止两个。可以分三类。
新课讲解
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。如4,6,15,49都是合数。
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。如2,3,5,7都是质数。
1既不是质数,也不是合数。
课堂练习
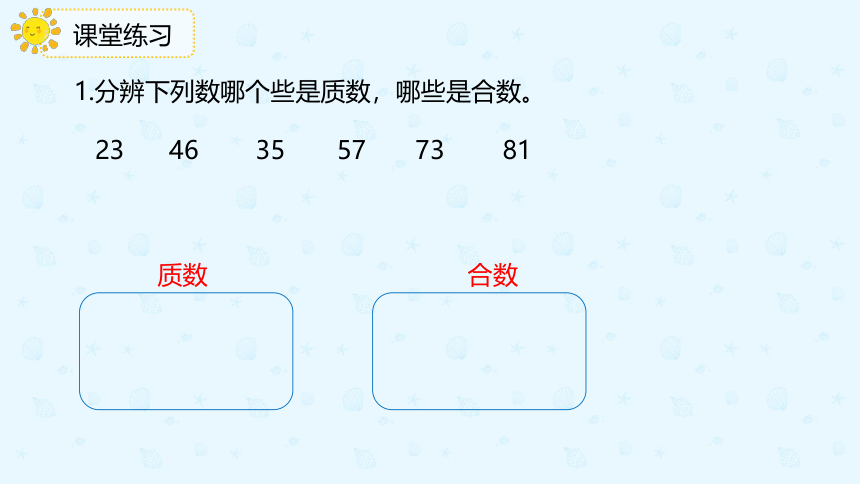
1.分辨下列数哪个些是质数,哪些是合数。
23
46
35
57
73
81
质数 合数
新课讲解
找出100以内的质数,做一个质数表。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
划去2的倍数(2除外)
划去3的倍数(3除外)
划去5的倍数(5除外)
划去7的倍数(7除外)
划去1
新课讲解
找出100以内的质数,做一个质数表。
2 3 5 7
11 13 17 19
23 29
31 37
41 43 47
53 59
61 67
71 73 79
83 89
97
新课讲解
1.根据质数和合数的概念判断,27 是质数还是合数?说出理由。
2. 判断下列各数是质数还是合数。
17 22 29 31 35 37 40 87 93 96
质数:17、29、31、37
合数:22、35、40、87、93、96
27是合数,因为它的因数有1、3、9、27,27是合数。
新课讲解
奇数
偶数
1 3 5 7 9 11 13 15 17 19
0 2 4 6 8 10 12 14 16 18 20
√
√
√
√
√
√
√
√
熟记 20 以内的质数(2、3、5、7、11、13、17、19)。
新课讲解
4. 思考下面的说法是否正确,说明理由。
(1)所有的奇数都是质数。( )
(2)所有的质数都是奇数。( )
(3)所有的合数都是偶数。( )
(4)所有的偶数都是合数。( )
×
×
×
×
新课讲解
5.猜猜我是谁。
我俩的和是10。
我俩都是质数,我俩的积是21。
新课讲解
将21写成两个质数相乘的形式,然后把两个质数相加,使结果等于10。
这两个质数分别是3和7。
21=3×7
5.猜猜我是谁。
3+7=10
课堂练习
6.按要求填数。
24
29
55
72
73
84
97
91
95
47
37
99
81
49
75
质数 合数
知识扩展
4=2+2,6=3+3,8=5+3,10=7+3,12=7+5,14=11+3……那么,是不是所有大于2的偶数,都可以表示为两个质数的和呢?
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。
哥德巴赫猜想看似简单,要证明却非常困难,成为数学中一个著名的难题,被称为“数学王冠上的明珠”。
哥德巴赫猜想
课堂小结
质数:只有1和它本身两个因数。
合数:至少有3个因数。
1既不是质数,也不是合数。
1、从教材课后习题中选取2、从练习册中选取。
课后作业
感 谢 聆 听
人教版 五年级下册
注:本课件所有素材来源于网络,如有侵权,请联系我们。
质数和合数
人教版 五年级下册
学习目标
质数、合数和奇数、偶数的区别。
知道100以内的质数,熟悉20以内的质数。
理解质数和合数的概念,知道它们之间的联系。能正确判断一个数是质数还是合数。
情境导入
想一想:因数的特征是什么?
2的因数有( )
1、2
1、3、5、15
一个数的因数的个数是有限的,最小的因数都是1,最大的因数是本身。
15的因数有( )
情境导入
自然数 1-20 中,奇数有哪些?偶数有哪些?
你知道它们是按什么标准分类的吗?
奇数:1,3,5,7,9,11,13,15,17,19。
偶数:2,4,6,8,10,12,14,16,18,20。
情境导入
找出1~20各数的因数,看看他们的因数个数有什么规律。
怎么找一个数的因数呢?
找一个数的因数从最小因数找起,一直找到它本身,哪两个数相乘的积等于这个数,那么这两个数就是这个数的因数。
新课讲解
请找出1-20 的的因数是多少。
数字 因数 个数 数字 因数 个数
1
1、2
1、3
1、2、4
1、5
1、2、3、6
1、7
1、2、4、8
1、3、9
1、2、5、10
1、11
1、2、3、4、6、12
1、13
1、2、7、14
1、3、5、15
1、2、8、16
1、17
1、2、3、6、9、18
1、19
1、2、4、5、10、20
1
2
2
3
2
4
2
4
3
4
2
6
2
4
4
4
2
6
2
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
新课讲解
只有一个因数 只有1和它本身两个因数 有两个以上的因数
1
2,3,5,7,11,13,17,19……
4,6,8,9,10,12,14,15,16,18,20……
有的数只有两个因数,如5的因数是1和5。
1只有一个因数1。
有的数的因数不止两个。可以分三类。
新课讲解
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。如4,6,15,49都是合数。
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。如2,3,5,7都是质数。
1既不是质数,也不是合数。
课堂练习
1.分辨下列数哪个些是质数,哪些是合数。
23
46
35
57
73
81
质数 合数
新课讲解
找出100以内的质数,做一个质数表。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
划去2的倍数(2除外)
划去3的倍数(3除外)
划去5的倍数(5除外)
划去7的倍数(7除外)
划去1
新课讲解
找出100以内的质数,做一个质数表。
2 3 5 7
11 13 17 19
23 29
31 37
41 43 47
53 59
61 67
71 73 79
83 89
97
新课讲解
1.根据质数和合数的概念判断,27 是质数还是合数?说出理由。
2. 判断下列各数是质数还是合数。
17 22 29 31 35 37 40 87 93 96
质数:17、29、31、37
合数:22、35、40、87、93、96
27是合数,因为它的因数有1、3、9、27,27是合数。
新课讲解
奇数
偶数
1 3 5 7 9 11 13 15 17 19
0 2 4 6 8 10 12 14 16 18 20
√
√
√
√
√
√
√
√
熟记 20 以内的质数(2、3、5、7、11、13、17、19)。
新课讲解
4. 思考下面的说法是否正确,说明理由。
(1)所有的奇数都是质数。( )
(2)所有的质数都是奇数。( )
(3)所有的合数都是偶数。( )
(4)所有的偶数都是合数。( )
×
×
×
×
新课讲解
5.猜猜我是谁。
我俩的和是10。
我俩都是质数,我俩的积是21。
新课讲解
将21写成两个质数相乘的形式,然后把两个质数相加,使结果等于10。
这两个质数分别是3和7。
21=3×7
5.猜猜我是谁。
3+7=10
课堂练习
6.按要求填数。
24
29
55
72
73
84
97
91
95
47
37
99
81
49
75
质数 合数
知识扩展
4=2+2,6=3+3,8=5+3,10=7+3,12=7+5,14=11+3……那么,是不是所有大于2的偶数,都可以表示为两个质数的和呢?
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。
哥德巴赫猜想看似简单,要证明却非常困难,成为数学中一个著名的难题,被称为“数学王冠上的明珠”。
哥德巴赫猜想
课堂小结
质数:只有1和它本身两个因数。
合数:至少有3个因数。
1既不是质数,也不是合数。
1、从教材课后习题中选取2、从练习册中选取。
课后作业
感 谢 聆 听
人教版 五年级下册
注:本课件所有素材来源于网络,如有侵权,请联系我们。
