人教A版2019必修第一册 4.4对数函数及其性质专项练习题 (word版含答案解析)
文档属性
| 名称 | 人教A版2019必修第一册 4.4对数函数及其性质专项练习题 (word版含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 69.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 15:28:54 | ||
图片预览




文档简介
4.4对数函数及其性质专项练习题
一.选择题(共8小题,满分40分,每小题5分)
1.下列函数是对数函数的是( )
A.y=log3(x+1)
B.y=loga(2x)(a>0,且a≠1)
C.y=lnx
D.
2.函数y的定义域为( )
A.(0,+∞) B.[0,+∞) C.(﹣1,+∞) D.[﹣1,+∞)
3.函数y=2+log2x(x≥1)的值域为( )
A.(2,+∞) B.(﹣∞,2) C.[2,+∞) D.[3,+∞)
4.已知,b=log32,,则a,b,c的大小关系为( )
A.a<b<c B.a<c<b C.c<a<b D.b<c<a
5.当a>1时,在同一坐标系中,函数y=ax与y=logax的图象是( )
A. B.
C. D.
6.“x<﹣2”是“ln(x+3)<0”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
7.函数f(x)的单调递增区间是( )
A. B. C. D.
8.若函数f(x)=loga(x2﹣ax+5),(a>0,a≠1)满足对任意的x1,x2,当x1<x2时f(x1)﹣f(x2)>0,则实数a的取值范围是( )
A.a>1 B.0<a<2 C.0<a<1 D.1<a<2
二.多选题(共4小题,满分20分,每小题5分)
9.设a=50.6,b=0.65,c=log0.60.5,d=log50.6,则在a,b,c,d这4个数中( )
A.最大数为a B.最小数为b C.最大数为c D.最小数为d
10.已知函数f(x)=|lgx|,则( )
A.f(x)是偶函数 B.f(x)值域为[0,+∞)
C.f(x)在[0,+∞)上递增 D.f(x)有一个零点
11.已知logb2021>loga2021>0,则下列结论正确的是( )
A.0.2a<0.2b B.
C.lnb﹣b>lna﹣a D.若m>0,则
12.如果函数f(x)=loga|x﹣1|在(0,1)上是减函数,那么( )
A.f(x)在(1,+∞)上递增且无最大值
B.f(x)在(1,+∞)递减且无最小值
C.f(x)在定义域内是偶函数
D.f(x)的图象关于直线x=1对称
三.填空题(共4小题,满分20分,每小题5分)
13.设a=log32,b=20.2,c=log20.2,则a,b,c从小到大的顺序为 .
14.已知函数f(x)=|ln(x+1)﹣1|,若a>b且f(a)=f(b),则a+b的取值范围是 .
15.已知函数f(x)=log2(x+1),若f(m2+2)<f(3m),则实数m的取值范围是 .
16.已知函数f(x)=loga(2x﹣a)在区间上恒有f(x)>0,则实数a的取值范围为 .
四.解答题(共6小题,满分70分)
17.设,比校a、b、c的大小,并说明理由.
18.已知函数f(x)=log2(x+1)﹣2.
(1)若f(x)>0,求x的取值范围.
(2)若x∈(﹣1,3],求f(x)的值域.
19.已知函数f(x)=logax(a>0,且a≠1)在区间上的最大值为2.
(1)求a的值;
(2)如果0<a<1,求使f(f(x)﹣2)>0成立的x的取值范围.
20.大西洋鲑鱼每年都要逆流而上,游回产地产卵.经研究发现鲑鱼的游速可以表示为函数,单位是m/s,其中O表示鱼的耗氧量的单位数.
(1)当一条鱼的耗氧量是900个单位时,它的游速是多少?
(2)某条鱼想把游速提高1m/s,那么它的耗氧量的单位数将如何变化?
21.已知f(x)是定义在R上的偶函数,且x≤0时,f(x)(﹣x+1)
(1)求f(3)+f(﹣1);
(2)求函数f(x)的解析式;
(3)若f(a﹣1)<﹣1,求实数a的取值范围.
22.如图,已知过原点O的直线与函数y=log8x的图像交于A,B两点,分别过点A,B作y轴的平行线与函数y=log2x的图像交于C,D两点.
(1)证明O,C,D三点在同一条直线上;
(2)当BC∥x轴时,求A点的坐标.
4.4对数函数及其性质专项练习题-参考答案
1、[分析]:根据对数函数的定义即可得出.
解:根据对数函数的定义可得:只有y=lnx为对数函数.
故选:C.
2、[分析]:根据二次根式以及对数函数的性质求出函数的定义域即可.
解:由题意得:
,解得:x>0,
故选:A.
3、[分析]:根据函数y=2+log2x可知其在[1,+∞)上单调递增,利用函数的单调性求得,当x=1时,y有最小值2,从而求得函数的值域.
解:∵函数y=2+log2x在[1,+∞)上单调递增,
∴当x=1时,y有最小值2,
即函数y=2+log2x(x≥1)的值域为[2,+∞).
故选:C.
4、[分析]:利用对数的性质,判断3个数值的大小即可.
解:0,b=log32∈(0,1),1,
所以a<b<c.
故选:A.
5、[分析]:根据底数与指数(对数)函数单调性即可判断.
解:a>1时,函数y=ax与y=logax的均为增函数,
故选:B.
6、[分析]:先求出对数不等式的解,再根据充分必要条件的定义即可判断.
解:ln(x+3)<0,则0<x+3<1,即﹣3<x<﹣2,
∴“x<﹣2”是“ln(x+3)<0”的必要不充分条件,
故选:B.
7、[分析]:先根据对数函数的真数大于零求定义域,再把复合函数分成二次函数和对数函数,分别在定义域内判断两个基本初等函数的单调性,再由“同增异减”求原函数的递增区间
解:要使函数有意义,则6+x﹣2x2>0,解得x<2,故函数的定义域是(,2)
令t=﹣2x2+x﹣6则函数t在(,)上递增,在[,2)上递减,
又因函数y在定义域上单调递减,
故由复合函数的单调性知y(6+x﹣2x2)的单调递增区间是[,2).
故选:B.
8、[分析]:对任意的x1,x2,当x1<x2时f(x1)﹣f(x2)>0,转化成函数f(x)在(﹣∞,]上单调递减,然后根据符合函数的单调性的性质建立关系式,解之即可求出所求.
解:对任意的x1,x2,当x1<x2时f(x1)﹣f(x2)>0,实质上就是“函数单调递减”的“伪装”,同时还隐含了“f(x)有意义”.
事实上由于g(x)=x2﹣ax+5在x时递减,
从而,由此得a的取值范围为(1,2),
故选:D.
9、[分析]:利用指数函数、对数函数的单调性直接求解.
解:∵a=50.6>50.5>40.5=2,
0<b=0.65<0.60=1,
1=log0.60.6<c=log0.60.5<log0.60.36=2,
d=log50.6<log51=0,
∴在a,b,c,d这4个数中最大的为a,最小的为d.
故选:AD.
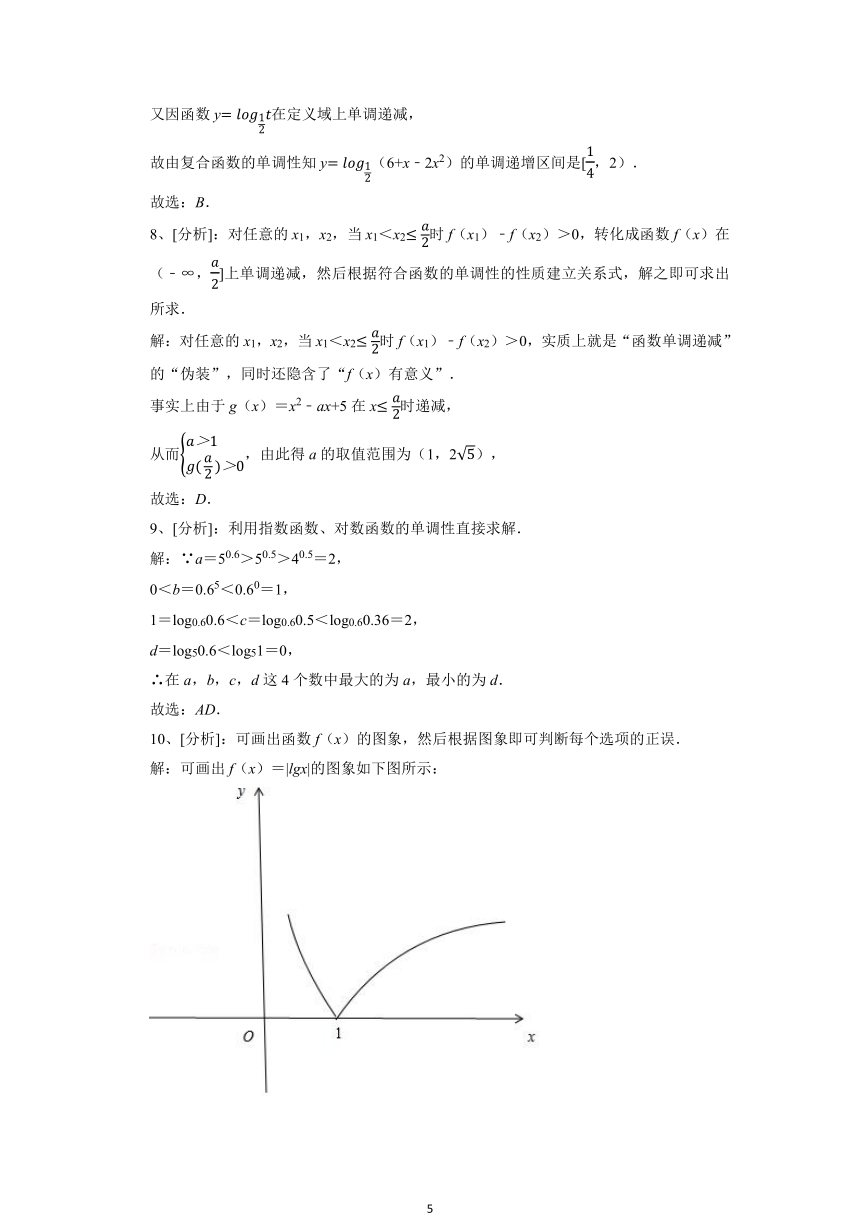
10、[分析]:可画出函数f(x)的图象,然后根据图象即可判断每个选项的正误.
解:可画出f(x)=|lgx|的图象如下图所示:
根据图象可看出f(x)的值域为[0,+∞),f(x)有一个零点.
故选:BD.
11、[分析]:推导出a>b>1,从而0.2a<0.2b,,;设y=lnx﹣x,x>1,则y′0,从而y=lnx﹣x,x>1是减函数,进而lnb﹣b>lna﹣a;再利用作差数判断D.
解:∵logb2021>loga2021>0,
∴,
∴log2021a>log2021b>0,
∴a>b>1,
对于A,∵a>b>1,∴0.2a<0.2b,故A正确;
对于B,∵a>b>1,∴,,故B错误;
对于C,设y=lnx﹣x,x>1,则y′0,∴y=lnx﹣x,x>1是减函数,
∵a>b>1,∴lnb﹣b>lna﹣a,故C正确;
对于D,∵a>b>1,m>0,
∴0,
∴若m>0,则,故D错误.
故选:AC.
12、[分析]:利用复合函数的单调性确定a的取值范围,然后再利用复合函数的单调性判断选项A,B即可,利用定义域即可判断选项C,由f(2﹣x)=f(x),即可判断选项D.
解:因为函数f(x)=loga|x﹣1|在(0,1)上是减函数,
所以f(x)=loga(1﹣x)在(0,1)上为减函数,
而y=1﹣x是减函数,
故a>1,
所以当x>1时,f(x)=loga(x﹣1),y=x﹣1是增函数,而a>1,
则f(x)在(1,+∞)上递增且无最大值,
故选项A正确,选项B错误;
函数f(x)=loga|x﹣1|的定义域为(﹣∞,1)∪(1,+∞),不关于原点对称,
所以f(x)为非奇非偶函数,
故选项C错误;
因为f(2﹣x)=loga|2﹣x﹣1|=loga|x﹣1|=f(x),
所以f(x)的图象关于直线x=1对称,
故选项D正确.
故选:AD.
13、[分析]:利用对数函数和指数函数的性质求解.
解:∵0=log31<log32<log33=1,∴0<a<1,
∵20.2>20=1,∴b>1,
∵log20.2<log21=0,∴c<0,
∴c<a<b,
故答案为:c<a<b.
14、[分析]:利用f(a)=f(b)得出a,b满足关系式(a+1)(b+1)=e ,代入a+b=(a+1)+(b+1)﹣2,消去b,构造函数求解.
解:因为,
所以﹣1<b<e﹣1<a,且﹣ln(b+1)+1=ln(a+1)﹣1,整理得(a+1)(b+1)=e .
所以a+b=(a+1)+(b+1)﹣2=(a+1)2,
设g(t)=t,则g(t)在(e,+∞)上单调递增,
所以g(t)>g(e)=2e﹣2.
故答案为:(2e﹣2,+∞)
15、[分析]:根据对数函数的定义域和单调性列出不等式组,解出不等式即可.
解:由题意可得函数的定义域为(﹣1,+∞),
又因为函数f(x)=log2(x+1)在(﹣1,+∞)单调递增,
∴有,解得,1<m<2,
所以实数m的取值范围为(1,2).
故答案为:(1,2).
16、[分析]:由题意利用对数函数的单调性和特殊点,函数的恒成立问题,求得实数a的取值范围.
解:函数f(x)=loga(2x﹣a)在区间上恒有f(x)>0,
即当a>1时,2x﹣a>1,或当0<a<1时,0<2x﹣a<1.
∴①,或②.
由①求得 a∈ ,由②求得 a.
综合可得实数a的取值范围为(,),
故答案为:(,).
17、[分析]:由对数的运算性质可得b>a>0,进一步分析c<0得答案.
解:log2(log48),
b=log2(log23)=log2(log49),
∴b>a>0,
又∵0<log32<1,∴c=log3(log32)<0.
∴b>a>c.
18、[分析]:(1)通过f(x)>0,列出不等式即可求x的取值范围.
(2)x∈(﹣1,3],求出x+1的范围,利用对数函数的单调性求解求f(x)的值域.
解:(1)函数f(x)=log2(x+1)﹣2,
∵f(x)>0,即log2(x+1)﹣2>0,
∴log2(x+1)>2,
∴x>3.
(2)∵x∈(﹣1,3],∴x+1∈(0,4],
∴log2(x+1)∈(﹣∞,2],
∴log2(x+1)﹣2∈(﹣∞,0].
所以f(x)的值域为(﹣∞,0].19、[分析]:(1)分类讨论a的范围,利用对数函数的单调性求出函数的最大值,从而得到a的值.
(2)由题意利用对数函数的单调性可得0<f(x)﹣2<1,即2<logax<3,由此求得a 的范围.
解:(1)∵函数f(x)=logax(a>0,且a≠1)在区间上是单调函数,
当a>1时,函数为增函数,最大值为loga3=2,故a.
当0<a<1时,函数为减函数,最大值为2,故a.
综上可得,a或.
(2)∵0<a<1,不等式f(f(x)﹣2)>0,即loga[f(x)﹣2]>0,
∴0<f(x)﹣2<1,即2<f(x)<3,即2<logax<3,
解得a3<x<a2,故x的范围为(a3,a2).
20、[分析]:(1)将O=900代入,直接求得结果.
(2)由v2﹣v1=1得,即耗氧量变为原来的九倍.
解:(1)当O=900时,lm/s
(2)由v2﹣v1=1得,所以耗氧量增大为原来的9倍.
21、[分析]:(1)利用函数奇偶性的性质即可求f(3)+f(﹣1)
(2)根据函数奇偶性的性质即可求函数f(x)的解析式;
(3)若f(a﹣1)<﹣1,将不等式进行转化即可求实数a的取值范围.
解:(I)∵f(x)是定义在R上的偶函数,x≤0时,f(x)(﹣x+1),
∴f(3)+f(﹣1)=f(﹣3)+f(﹣1)42=﹣2﹣1=﹣3;
(II)令x>0,则﹣x<0,f(﹣x)(x+1)=f(x)
∴x>0时,f(x)(x+1),
则f(x).
(Ⅲ)∵f(x)(﹣x+1)在(﹣∞,0]上为增函数,
∴f(x)在(0,+∞)上为减函数
∵f(a﹣1)<﹣1=f(1)
∴|a﹣1|>1,
∴a>2或a<0
22、[分析]:(1)设A(x1,log8x1),B(x2,log8x2),由题意可知C(x1,log2x1),D(x2,log2x2),由题意可知kOA=kOB,即,利用对数的运算性质化简可得kOC=kOD,即点O,C,D三点在同一条直线上.
(2))由BC∥x轴可得,代入可得0,结合x1>0求出x1的值,得到A点的坐标.
证明:(1)设A(x1,log8x1),B(x2,log8x2),由题意可知C(x1,log2x1),D(x2,log2x2),
∵A,B在过点O的直线上,∴kOA=kOB,
∴,∴,
∴,即kOC=kOD,
∴点O,C,D三点在同一条直线上.
解:(2)∵BC∥x轴,∴log2x1=log8x2,即3log2x1=log2x2,
∴,
由(1)知,∴3x1log2x1
∴0,
∵x1>0,
∴log2x1=0或
∴x1=1 或,
当x1=1 时,A,B两点重合,不符合题意,舍去,
∴A点的坐标为(,)
一.选择题(共8小题,满分40分,每小题5分)
1.下列函数是对数函数的是( )
A.y=log3(x+1)
B.y=loga(2x)(a>0,且a≠1)
C.y=lnx
D.
2.函数y的定义域为( )
A.(0,+∞) B.[0,+∞) C.(﹣1,+∞) D.[﹣1,+∞)
3.函数y=2+log2x(x≥1)的值域为( )
A.(2,+∞) B.(﹣∞,2) C.[2,+∞) D.[3,+∞)
4.已知,b=log32,,则a,b,c的大小关系为( )
A.a<b<c B.a<c<b C.c<a<b D.b<c<a
5.当a>1时,在同一坐标系中,函数y=ax与y=logax的图象是( )
A. B.
C. D.
6.“x<﹣2”是“ln(x+3)<0”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
7.函数f(x)的单调递增区间是( )
A. B. C. D.
8.若函数f(x)=loga(x2﹣ax+5),(a>0,a≠1)满足对任意的x1,x2,当x1<x2时f(x1)﹣f(x2)>0,则实数a的取值范围是( )
A.a>1 B.0<a<2 C.0<a<1 D.1<a<2
二.多选题(共4小题,满分20分,每小题5分)
9.设a=50.6,b=0.65,c=log0.60.5,d=log50.6,则在a,b,c,d这4个数中( )
A.最大数为a B.最小数为b C.最大数为c D.最小数为d
10.已知函数f(x)=|lgx|,则( )
A.f(x)是偶函数 B.f(x)值域为[0,+∞)
C.f(x)在[0,+∞)上递增 D.f(x)有一个零点
11.已知logb2021>loga2021>0,则下列结论正确的是( )
A.0.2a<0.2b B.
C.lnb﹣b>lna﹣a D.若m>0,则
12.如果函数f(x)=loga|x﹣1|在(0,1)上是减函数,那么( )
A.f(x)在(1,+∞)上递增且无最大值
B.f(x)在(1,+∞)递减且无最小值
C.f(x)在定义域内是偶函数
D.f(x)的图象关于直线x=1对称
三.填空题(共4小题,满分20分,每小题5分)
13.设a=log32,b=20.2,c=log20.2,则a,b,c从小到大的顺序为 .
14.已知函数f(x)=|ln(x+1)﹣1|,若a>b且f(a)=f(b),则a+b的取值范围是 .
15.已知函数f(x)=log2(x+1),若f(m2+2)<f(3m),则实数m的取值范围是 .
16.已知函数f(x)=loga(2x﹣a)在区间上恒有f(x)>0,则实数a的取值范围为 .
四.解答题(共6小题,满分70分)
17.设,比校a、b、c的大小,并说明理由.
18.已知函数f(x)=log2(x+1)﹣2.
(1)若f(x)>0,求x的取值范围.
(2)若x∈(﹣1,3],求f(x)的值域.
19.已知函数f(x)=logax(a>0,且a≠1)在区间上的最大值为2.
(1)求a的值;
(2)如果0<a<1,求使f(f(x)﹣2)>0成立的x的取值范围.
20.大西洋鲑鱼每年都要逆流而上,游回产地产卵.经研究发现鲑鱼的游速可以表示为函数,单位是m/s,其中O表示鱼的耗氧量的单位数.
(1)当一条鱼的耗氧量是900个单位时,它的游速是多少?
(2)某条鱼想把游速提高1m/s,那么它的耗氧量的单位数将如何变化?
21.已知f(x)是定义在R上的偶函数,且x≤0时,f(x)(﹣x+1)
(1)求f(3)+f(﹣1);
(2)求函数f(x)的解析式;
(3)若f(a﹣1)<﹣1,求实数a的取值范围.
22.如图,已知过原点O的直线与函数y=log8x的图像交于A,B两点,分别过点A,B作y轴的平行线与函数y=log2x的图像交于C,D两点.
(1)证明O,C,D三点在同一条直线上;
(2)当BC∥x轴时,求A点的坐标.
4.4对数函数及其性质专项练习题-参考答案
1、[分析]:根据对数函数的定义即可得出.
解:根据对数函数的定义可得:只有y=lnx为对数函数.
故选:C.
2、[分析]:根据二次根式以及对数函数的性质求出函数的定义域即可.
解:由题意得:
,解得:x>0,
故选:A.
3、[分析]:根据函数y=2+log2x可知其在[1,+∞)上单调递增,利用函数的单调性求得,当x=1时,y有最小值2,从而求得函数的值域.
解:∵函数y=2+log2x在[1,+∞)上单调递增,
∴当x=1时,y有最小值2,
即函数y=2+log2x(x≥1)的值域为[2,+∞).
故选:C.
4、[分析]:利用对数的性质,判断3个数值的大小即可.
解:0,b=log32∈(0,1),1,
所以a<b<c.
故选:A.
5、[分析]:根据底数与指数(对数)函数单调性即可判断.
解:a>1时,函数y=ax与y=logax的均为增函数,
故选:B.
6、[分析]:先求出对数不等式的解,再根据充分必要条件的定义即可判断.
解:ln(x+3)<0,则0<x+3<1,即﹣3<x<﹣2,
∴“x<﹣2”是“ln(x+3)<0”的必要不充分条件,
故选:B.
7、[分析]:先根据对数函数的真数大于零求定义域,再把复合函数分成二次函数和对数函数,分别在定义域内判断两个基本初等函数的单调性,再由“同增异减”求原函数的递增区间
解:要使函数有意义,则6+x﹣2x2>0,解得x<2,故函数的定义域是(,2)
令t=﹣2x2+x﹣6则函数t在(,)上递增,在[,2)上递减,
又因函数y在定义域上单调递减,
故由复合函数的单调性知y(6+x﹣2x2)的单调递增区间是[,2).
故选:B.
8、[分析]:对任意的x1,x2,当x1<x2时f(x1)﹣f(x2)>0,转化成函数f(x)在(﹣∞,]上单调递减,然后根据符合函数的单调性的性质建立关系式,解之即可求出所求.
解:对任意的x1,x2,当x1<x2时f(x1)﹣f(x2)>0,实质上就是“函数单调递减”的“伪装”,同时还隐含了“f(x)有意义”.
事实上由于g(x)=x2﹣ax+5在x时递减,
从而,由此得a的取值范围为(1,2),
故选:D.
9、[分析]:利用指数函数、对数函数的单调性直接求解.
解:∵a=50.6>50.5>40.5=2,
0<b=0.65<0.60=1,
1=log0.60.6<c=log0.60.5<log0.60.36=2,
d=log50.6<log51=0,
∴在a,b,c,d这4个数中最大的为a,最小的为d.
故选:AD.
10、[分析]:可画出函数f(x)的图象,然后根据图象即可判断每个选项的正误.
解:可画出f(x)=|lgx|的图象如下图所示:
根据图象可看出f(x)的值域为[0,+∞),f(x)有一个零点.
故选:BD.
11、[分析]:推导出a>b>1,从而0.2a<0.2b,,;设y=lnx﹣x,x>1,则y′0,从而y=lnx﹣x,x>1是减函数,进而lnb﹣b>lna﹣a;再利用作差数判断D.
解:∵logb2021>loga2021>0,
∴,
∴log2021a>log2021b>0,
∴a>b>1,
对于A,∵a>b>1,∴0.2a<0.2b,故A正确;
对于B,∵a>b>1,∴,,故B错误;
对于C,设y=lnx﹣x,x>1,则y′0,∴y=lnx﹣x,x>1是减函数,
∵a>b>1,∴lnb﹣b>lna﹣a,故C正确;
对于D,∵a>b>1,m>0,
∴0,
∴若m>0,则,故D错误.
故选:AC.
12、[分析]:利用复合函数的单调性确定a的取值范围,然后再利用复合函数的单调性判断选项A,B即可,利用定义域即可判断选项C,由f(2﹣x)=f(x),即可判断选项D.
解:因为函数f(x)=loga|x﹣1|在(0,1)上是减函数,
所以f(x)=loga(1﹣x)在(0,1)上为减函数,
而y=1﹣x是减函数,
故a>1,
所以当x>1时,f(x)=loga(x﹣1),y=x﹣1是增函数,而a>1,
则f(x)在(1,+∞)上递增且无最大值,
故选项A正确,选项B错误;
函数f(x)=loga|x﹣1|的定义域为(﹣∞,1)∪(1,+∞),不关于原点对称,
所以f(x)为非奇非偶函数,
故选项C错误;
因为f(2﹣x)=loga|2﹣x﹣1|=loga|x﹣1|=f(x),
所以f(x)的图象关于直线x=1对称,
故选项D正确.
故选:AD.
13、[分析]:利用对数函数和指数函数的性质求解.
解:∵0=log31<log32<log33=1,∴0<a<1,
∵20.2>20=1,∴b>1,
∵log20.2<log21=0,∴c<0,
∴c<a<b,
故答案为:c<a<b.
14、[分析]:利用f(a)=f(b)得出a,b满足关系式(a+1)(b+1)=e ,代入a+b=(a+1)+(b+1)﹣2,消去b,构造函数求解.
解:因为,
所以﹣1<b<e﹣1<a,且﹣ln(b+1)+1=ln(a+1)﹣1,整理得(a+1)(b+1)=e .
所以a+b=(a+1)+(b+1)﹣2=(a+1)2,
设g(t)=t,则g(t)在(e,+∞)上单调递增,
所以g(t)>g(e)=2e﹣2.
故答案为:(2e﹣2,+∞)
15、[分析]:根据对数函数的定义域和单调性列出不等式组,解出不等式即可.
解:由题意可得函数的定义域为(﹣1,+∞),
又因为函数f(x)=log2(x+1)在(﹣1,+∞)单调递增,
∴有,解得,1<m<2,
所以实数m的取值范围为(1,2).
故答案为:(1,2).
16、[分析]:由题意利用对数函数的单调性和特殊点,函数的恒成立问题,求得实数a的取值范围.
解:函数f(x)=loga(2x﹣a)在区间上恒有f(x)>0,
即当a>1时,2x﹣a>1,或当0<a<1时,0<2x﹣a<1.
∴①,或②.
由①求得 a∈ ,由②求得 a.
综合可得实数a的取值范围为(,),
故答案为:(,).
17、[分析]:由对数的运算性质可得b>a>0,进一步分析c<0得答案.
解:log2(log48),
b=log2(log23)=log2(log49),
∴b>a>0,
又∵0<log32<1,∴c=log3(log32)<0.
∴b>a>c.
18、[分析]:(1)通过f(x)>0,列出不等式即可求x的取值范围.
(2)x∈(﹣1,3],求出x+1的范围,利用对数函数的单调性求解求f(x)的值域.
解:(1)函数f(x)=log2(x+1)﹣2,
∵f(x)>0,即log2(x+1)﹣2>0,
∴log2(x+1)>2,
∴x>3.
(2)∵x∈(﹣1,3],∴x+1∈(0,4],
∴log2(x+1)∈(﹣∞,2],
∴log2(x+1)﹣2∈(﹣∞,0].
所以f(x)的值域为(﹣∞,0].19、[分析]:(1)分类讨论a的范围,利用对数函数的单调性求出函数的最大值,从而得到a的值.
(2)由题意利用对数函数的单调性可得0<f(x)﹣2<1,即2<logax<3,由此求得a 的范围.
解:(1)∵函数f(x)=logax(a>0,且a≠1)在区间上是单调函数,
当a>1时,函数为增函数,最大值为loga3=2,故a.
当0<a<1时,函数为减函数,最大值为2,故a.
综上可得,a或.
(2)∵0<a<1,不等式f(f(x)﹣2)>0,即loga[f(x)﹣2]>0,
∴0<f(x)﹣2<1,即2<f(x)<3,即2<logax<3,
解得a3<x<a2,故x的范围为(a3,a2).
20、[分析]:(1)将O=900代入,直接求得结果.
(2)由v2﹣v1=1得,即耗氧量变为原来的九倍.
解:(1)当O=900时,lm/s
(2)由v2﹣v1=1得,所以耗氧量增大为原来的9倍.
21、[分析]:(1)利用函数奇偶性的性质即可求f(3)+f(﹣1)
(2)根据函数奇偶性的性质即可求函数f(x)的解析式;
(3)若f(a﹣1)<﹣1,将不等式进行转化即可求实数a的取值范围.
解:(I)∵f(x)是定义在R上的偶函数,x≤0时,f(x)(﹣x+1),
∴f(3)+f(﹣1)=f(﹣3)+f(﹣1)42=﹣2﹣1=﹣3;
(II)令x>0,则﹣x<0,f(﹣x)(x+1)=f(x)
∴x>0时,f(x)(x+1),
则f(x).
(Ⅲ)∵f(x)(﹣x+1)在(﹣∞,0]上为增函数,
∴f(x)在(0,+∞)上为减函数
∵f(a﹣1)<﹣1=f(1)
∴|a﹣1|>1,
∴a>2或a<0
22、[分析]:(1)设A(x1,log8x1),B(x2,log8x2),由题意可知C(x1,log2x1),D(x2,log2x2),由题意可知kOA=kOB,即,利用对数的运算性质化简可得kOC=kOD,即点O,C,D三点在同一条直线上.
(2))由BC∥x轴可得,代入可得0,结合x1>0求出x1的值,得到A点的坐标.
证明:(1)设A(x1,log8x1),B(x2,log8x2),由题意可知C(x1,log2x1),D(x2,log2x2),
∵A,B在过点O的直线上,∴kOA=kOB,
∴,∴,
∴,即kOC=kOD,
∴点O,C,D三点在同一条直线上.
解:(2)∵BC∥x轴,∴log2x1=log8x2,即3log2x1=log2x2,
∴,
由(1)知,∴3x1log2x1
∴0,
∵x1>0,
∴log2x1=0或
∴x1=1 或,
当x1=1 时,A,B两点重合,不符合题意,舍去,
∴A点的坐标为(,)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
