2021-2022学年冀教版八年级数学上册17.2直角三角形 解答题练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册17.2直角三角形 解答题练习 (word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 19:21:56 | ||
图片预览

文档简介
2021-2022学年冀教版八年级数学上册《17.2直角三角形》解答题专题练习(附答案)
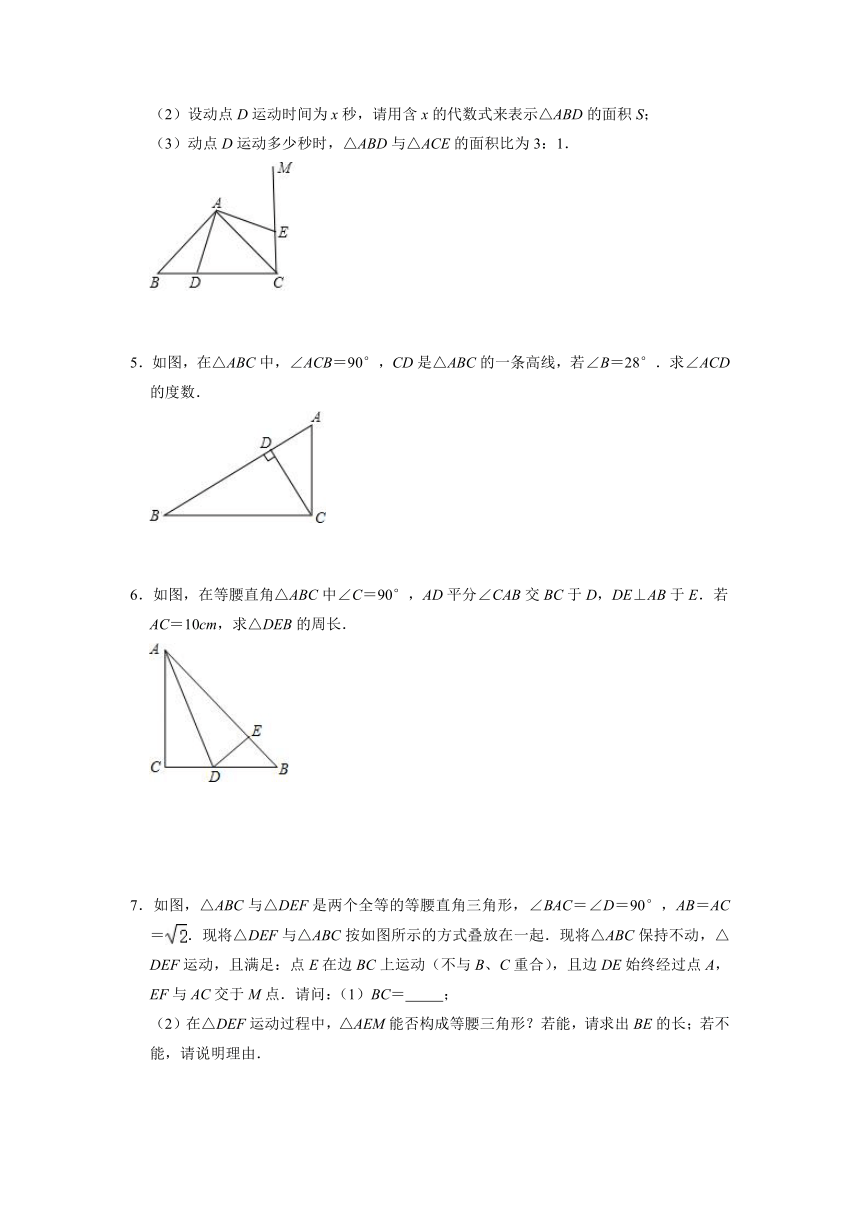
1.如图,OE平分∠AOB,且EC⊥OA,ED⊥OB,垂足分别是C、D.
(1)求证∠1=∠2;
(2)求证:OE是线段CD的垂直平分线.
2.已知在△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB,AC上的动点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)在(1)的条件下,四边形AEDF的面积是否变化,证明你的结论;
(3)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
3.如图,在△ABC中,∠ACB=90°,CD⊥AB,AF是角平分线,交CD于点E.求证:∠1=∠2.
4.如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始以每秒2cm的速度运动到B点,动点E也同时从点C开始沿射线CM方向以每秒1cm的速度运动.
(1)问动点D运动多少秒时,△ABD≌△ACE,并说明理由;
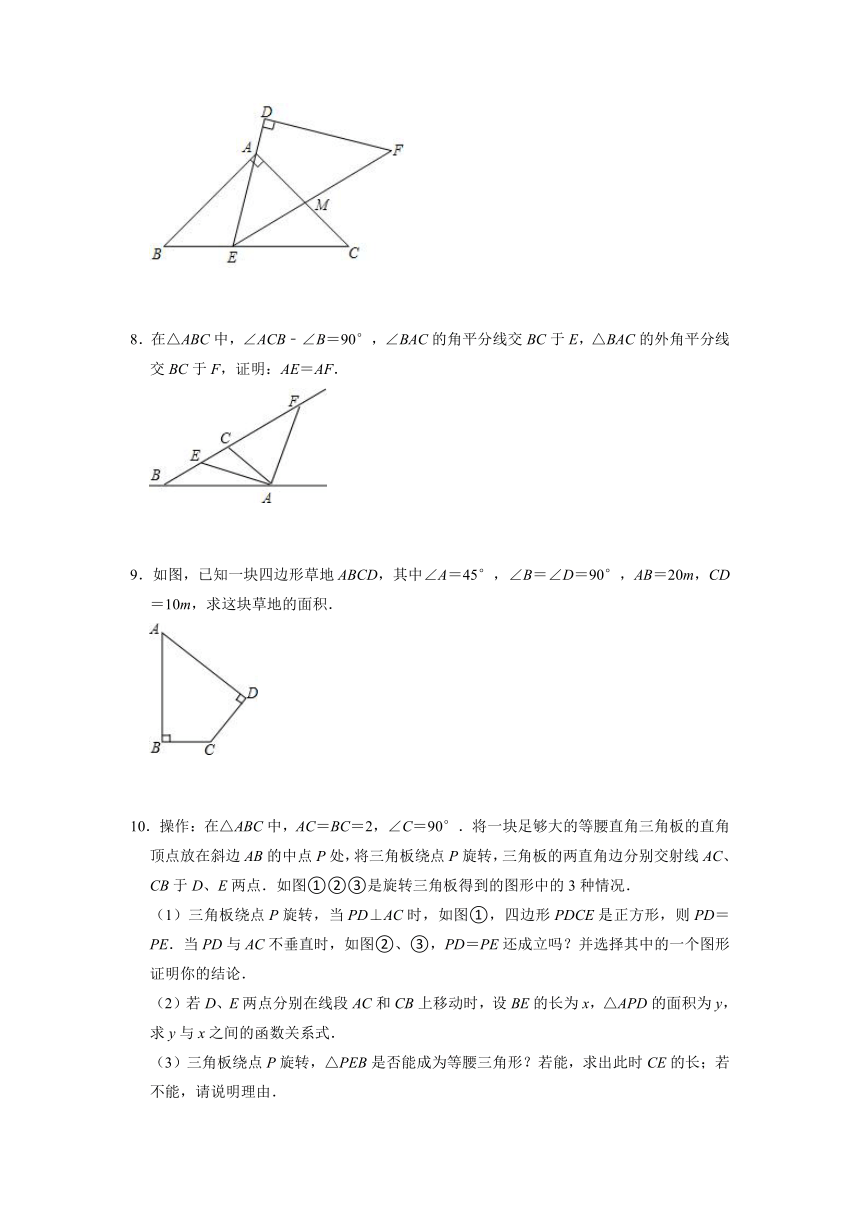
(2)设动点D运动时间为x秒,请用含x的代数式来表示△ABD的面积S;
(3)动点D运动多少秒时,△ABD与△ACE的面积比为3:1.
5.如图,在△ABC中,∠ACB=90°,CD是△ABC的一条高线,若∠B=28°.求∠ACD的度数.
6.如图,在等腰直角△ABC中∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E.若AC=10cm,求△DEB的周长.
7.如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:(1)BC= ;
(2)在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.
8.在△ABC中,∠ACB﹣∠B=90°,∠BAC的角平分线交BC于E,△BAC的外角平分线交BC于F,证明:AE=AF.
9.如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
10.操作:在△ABC中,AC=BC=2,∠C=90°.将一块足够大的等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①②③是旋转三角板得到的图形中的3种情况.
(1)三角板绕点P旋转,当PD⊥AC时,如图①,四边形PDCE是正方形,则PD=PE.当PD与AC不垂直时,如图②、③,PD=PE还成立吗?并选择其中的一个图形证明你的结论.
(2)若D、E两点分别在线段AC和CB上移动时,设BE的长为x,△APD的面积为y,求y与x之间的函数关系式.
(3)三角板绕点P旋转,△PEB是否能成为等腰三角形?若能,求出此时CE的长;若不能,请说明理由.
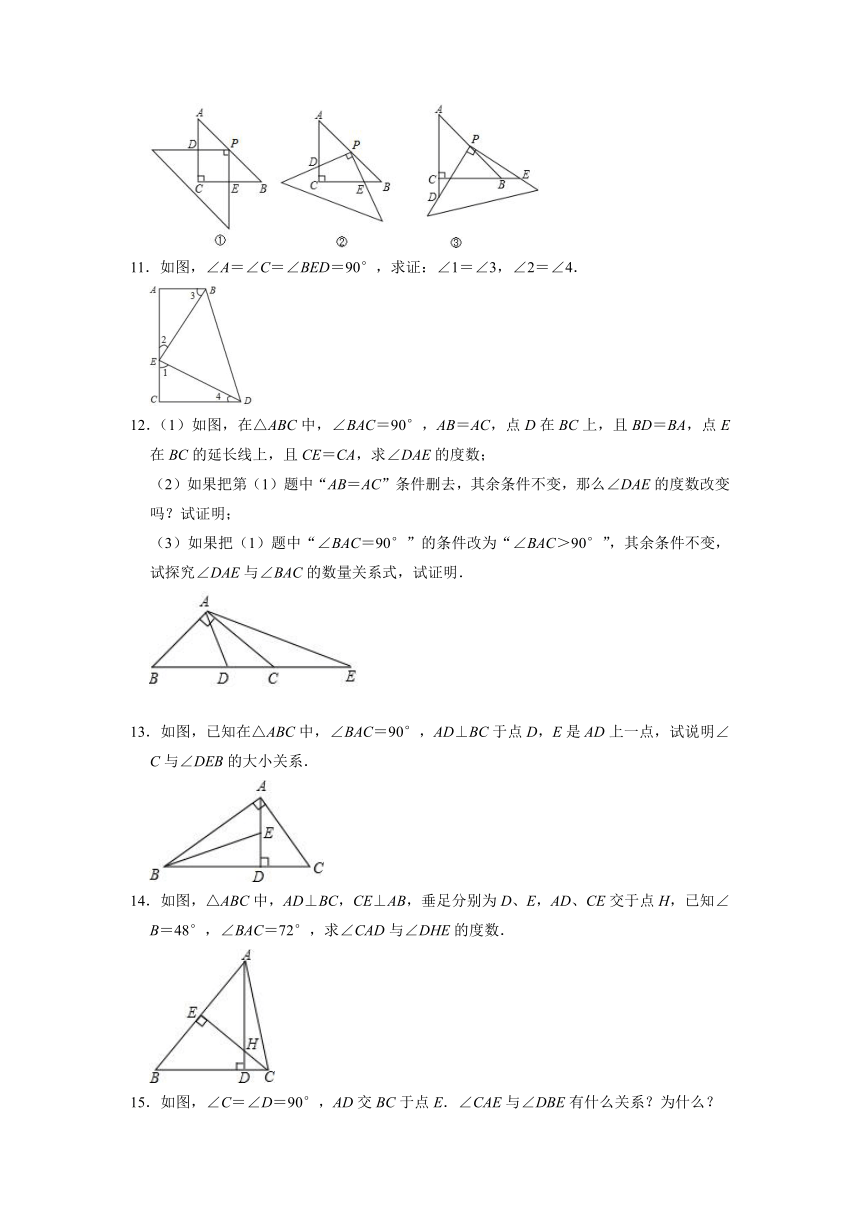
11.如图,∠A=∠C=∠BED=90°,求证:∠1=∠3,∠2=∠4.
12.(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,求∠DAE的度数;
(2)如果把第(1)题中“AB=AC”条件删去,其余条件不变,那么∠DAE的度数改变吗?试证明;
(3)如果把(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
13.如图,已知在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,试说明∠C与∠DEB的大小关系.
14.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知∠B=48°,∠BAC=72°,求∠CAD与∠DHE的度数.
15.如图,∠C=∠D=90°,AD交BC于点E.∠CAE与∠DBE有什么关系?为什么?
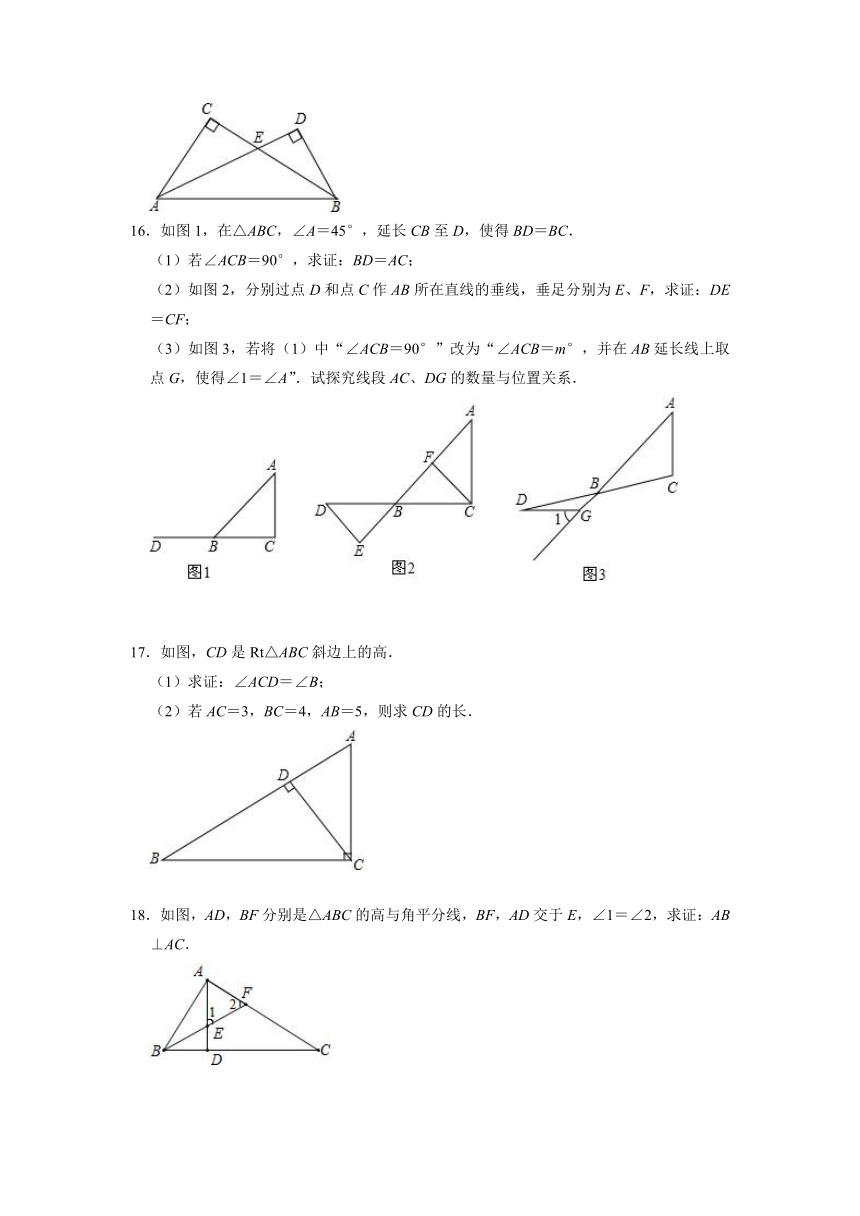
16.如图1,在△ABC,∠A=45°,延长CB至D,使得BD=BC.
(1)若∠ACB=90°,求证:BD=AC;
(2)如图2,分别过点D和点C作AB所在直线的垂线,垂足分别为E、F,求证:DE=CF;
(3)如图3,若将(1)中“∠ACB=90°”改为“∠ACB=m°,并在AB延长线上取点G,使得∠1=∠A”.试探究线段AC、DG的数量与位置关系.
17.如图,CD是Rt△ABC斜边上的高.
(1)求证:∠ACD=∠B;
(2)若AC=3,BC=4,AB=5,则求CD的长.
18.如图,AD,BF分别是△ABC的高与角平分线,BF,AD交于E,∠1=∠2,求证:AB⊥AC.
19.如图,由一副三角尺拼成的图形,写出∠C,∠EAD,∠CBE的度数.
20.在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过点B作BD⊥BC,交CF的延长线于点D,若∠D=65°,求∠EAC的度数.
21.已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
(1)求证:AE=BE;
(2)若∠AEC=45°,AC=1,求CE的长.
22.如图,已知在等腰Rt△BCD中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E,H是BC边的中点,连接DH与BE相交于点G
(1)试说明:△FBD≌△ACD;
(2)试说明:△ABC是等腰三角形;
(3)试说明:CE=BF;
(4)求BG:GE的值(直接写出答案).
23.已知△ABC中,∠BAC=90°,AB=AC.
(1)如图,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
若点D在AC的延长线上,如图,其他条件同(1),请画出此时的图形,并猜想BD与AE是否仍然相等?说明你的理由.
24.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
25.如图,已知∠CDF=∠OEF=90°,CE与OA相交于点F,若∠C=20°,求∠O的大小.
26.如图,等腰直角△ABC中,∠ACB=90°,D为CB延长线上一点,AE=AD,且AE⊥AD,BE与AC的延长线交于点P.
(1)求证:BP=PE;
(2)若AC=3PC,求的值.
27.如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
28.已知:如图,CE⊥AD,垂足为E,∠A=∠C,求证:AB⊥CD.
参考答案
1.证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴CE=DE,
∴∠1=∠2;
(2)在△OCE和△ODE中,,
∴△OCE≌△ODE(HL),
∴OC=OD,
又∵CE=DE,
∴OE是线段CD的垂直平分线.
2.(1)证明:连接AD
∵AB=AC,∠A=90°,D为BC中点
∴AD==BD=CD
且AD平分∠BAC
∴∠BAD=∠CAD=45°
在△BDE和△ADF中,
∴△BDE≌△ADF(SAS)
∴DE=DF,∠BDE=∠ADF
∵∠BDE+∠ADE=90°
∴∠ADF+∠ADE=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
(2)解:四边形AEDF面积不变.
理由:∵由(1)可知,△AFD≌△BED
∴S△BDE=S△ADF,
而S四边形AEDF=S△AED+S△ADF=S△AED+S△BDE=S△ABD
∴S四边形AEDF不会发生变化.
(3)解:仍为等腰直角三角形.
理由:∵△AFD≌△BED
∴DF=DE,∠ADF=∠BDE
∵∠ADF+∠FDB=90°
∴∠BDE+∠FDB=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
3.证明:∵AF是角平分线,
∴∠CAF=∠BAF,
∵∠ACB=90°,CD⊥AB,
∴∠CAF+∠2=90°,∠BAF+∠AED=90°,
∴∠2=∠AED,
∵∠1=∠AED,
∴∠1=∠2.
4.解:(1)如图1,设动点D运动t秒时,△ABD≌△ACE,
由题意得:CD=2t,CE=t,则BD=6﹣2t,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵CM⊥BC,
∴∠BCM=90°,
∴∠ACE=90°﹣45°=45°,
∴∠ACE=∠B,
∴当BD=CE时,△ABD≌△ACE,
即6﹣2t=t,
t=2,
答:动点D运动2秒时,△ABD≌△ACE;
(2)如图2,过A作AF⊥BC于F,
∵AB=AC,∠BAC=90°,
∴AF是斜边的中线,
∴AF=BC=×6=3,
由题意得:CD=2x,则BD=6﹣2x,
∴S=S△ABD=BD AF=(6﹣2x)×3=﹣3x+9;
(3)设动点D运动x秒时,△ABD与△ACE的面积比为3:1,
如图2,再过A作AG⊥CM于G,
∵∠AFC=∠BCM=∠AGC=90°,
∴四边形AFCG是矩形,
∴AG=CF=BC=3,
∵△ABD与△ACE的面积比为3:1,
∴==,
∴=3,
∴BD=3CE,
即6﹣2x=3x,
5x=6,
x=,
∴动点D运动秒时,△ABD与△ACE的面积比为3:1.
5.解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD是△ABC的一条高线,
∴∠B+∠BCD=90°,
∴∠ACD=∠B=28°.
6.解:∵DE⊥AB,
∴∠C=∠AED=90°,
∵AD平分∠CAB,
∴∠CAD=∠EAD,
在△ACD和△AED中,
,
∴△ACD≌△AED(AAS),
∴AC=AE,CD=DE,
∴BD+DE=BD+CD=BC=AC=AE,
在Rt△ACB中,AB=AC=10,
∴BD+DE+BE=AE+BE=AB=10,
所以,△DEB的周长为10cm.
7.解:(1)∵△ABC是等腰直角三角形,∠BAC=90°,AB=AC=,
∴BC==2,
故答案为:2;
(2)①若AE=AM 则∠AME=∠AEM=45°,
∵∠C=45°,
∴∠AME=∠C,
又∵∠AME>∠C,
∴这种情况不成立;
②若AE=EM,
∵∠B=∠AEM=45°,
∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°,
∴∠BAE=∠MEC,
在△ABE和△ECM中,
,
∴△ABE≌△ECM(AAS),
∴CE=AB=,
∵BC=2,
∴BE=2﹣;
③若MA=ME 则∠MAE=∠AEM=45°,
∵∠BAC=90°,
∴∠BAE=45°,
∴AE平分∠BAC,
∵AB=AC,
∴BE==1.
8.证明:∵AE平分∠BAC,AF是△BAC的外角的平分线,
∴∠EAF=∠EAC+∠CAF=(∠BAC+∠CAD)=90°,
∴△EAF是直角三角形,
∵∠ACB﹣∠B=90°,
∴∠BAC=180°﹣∠ACB﹣∠B=180°﹣(90°+∠B)﹣∠B=90°﹣2∠B,
∴∠BAE=∠BAC=45°﹣∠B,
∴∠AEC=∠BAE+∠B=45°,
∴∠AFE=45°,
∴∠AEC=∠AFE,
∴AE=AF.
9.解:分别延长AD,BC交于点E.如图所示,
∵∠A=45°,∠B=∠D=90°,
∴∠DCE=∠DEB=∠A=45°,
∴AB=BE,CD=DE,
∵AB=20,CD=10,
∴BE=20,DE=10,
∵S△ABE=AB BE=200,S△CDE=CD DE=50,
∴四边形ABCD的面积=S△ABE﹣S△CDE=200﹣50=150m2.
即这块草地的面积为:150m2.
10.解:(1)PD=PE依然成立.
证明:如图②,连接PC,∵△ABC是等腰直角三角形,P是AB中点,
∴CP=PB,CP⊥AB,∠ACP=∠ACB=45°,
即∠ACP=∠B=45°,
∵∠DPC+∠CPE=∠BPE+∠CPE=90°,
∴∠DPC=∠BPE,
∴△PCD≌△PBE,
∴PD=PE.
(2)由(1)得CP⊥AB,∠ACP=∠ACB=45°,
∴△ACP是等腰直角三角形,
∴AP=CP,△PCD≌△PBE,
∴CD=BE=x,
∴AD=AC﹣CD=2﹣x,
过点P作PF⊥AC于点F,则PF=AC=1,
∴△APD的面积y=AD PF=(2﹣x)×1,
即y=1﹣x.
(3)分三种情况讨论如下:
①当PE=PB时,点C与点E重合,即CE=0.
②当PE=BE时,CE=1.
③当BE=PB时,
若点E在线段CB上时,CE=2﹣;
若点E在CB延长线上时CE=2+.
11.证明:∵∠BED=90°,
∴∠1+∠2=180°﹣90°=90°,
∵∠A=90°,
∴∠2+∠3=90°,
∴∠1=∠3;
同理可得∠2=∠4.
12.解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=(180°﹣∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E=∠ACB=22.5°,
在△ABE中,∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=112.5°﹣67.5°=45度;
(2)不改变.
设∠CAE=x,
∵CA=CE,
∴∠E=∠CAE=x,
∴∠ACB=∠CAE+∠E=2x,
在△ABC中,∠BAC=90°,
∴∠B=90°﹣∠ACB=90°﹣2x,
∵BD=BA,
∴∠BAD=∠BDA=(180°﹣∠B)=x+45°,
在△ABE中,∠BAE=180°﹣∠B﹣∠E,
=180°﹣(90°﹣2x)﹣x=90°+x,
∴∠DAE=∠BAE﹣∠BAD,
=(90°+x)﹣(x+45°)=45°;
(3)∠DAE=∠BAC.
理由:设∠CAE=x,∠BAD=y,
则∠B=180°﹣2y,∠E=∠CAE=x,
∴∠BAE=180°﹣∠B﹣∠E=2y﹣x,
∴∠DAE=∠BAE﹣∠BAD=2y﹣x﹣y=y﹣x,
∠BAC=∠BAE﹣∠CAE=2y﹣x﹣x=2y﹣2x,
∴∠DAE=∠BAC.
13.答:∠C<∠DEB.
证明:∵∠BAC=90°,∴∠BAE+∠CAE=90°,
∵AD⊥BC,∴∠C+∠CAE=90°,
∴∠C=∠BAE,
∵∠BAE<∠DEB,
∴∠C<∠DEB.
14.解:∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣48°=42°,
∴∠CAD=∠BAC﹣∠BAD=30°,
∵CE⊥AB,
∴∠AEC=90°,
由三角形的外角性质得,∠DHE=∠BAD+∠AEH=42°+90°=132°.
15.解:∠CAE与∠DBE相等.
理由如下:∵在△CAE,△DBE中,∠C=∠D=90°,∠CEA=∠DEB,
∴∠CAE=90°﹣∠CEA,∠DBE=90°﹣∠DEB,
即∠CAE=∠DBE.
16.(1)证明:∵∠A=45°,∠ACB=90°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵BD=BC,
∴BD=AC;
(2)证明:∵DE⊥AB,CF⊥AB,
∴∠E=∠CFB=90°,
在△DBE与△CBF中,
∵,
∴△DBE≌△CBF(AAS),
∴DE=CF;
(3)解:DG=AC,DG⊥AC.
证明:过点C作CE∥DG交AB于点E,
∴∠2=∠3,
∵∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠4,
∵∠1=∠A,
∴∠4=∠A,
∴AC=CE,
在△DBG与△CBE中,
∵,
∴△DBG≌△CBE(AAS),
∴CE=DG,
∴DG=AC.
∵∠A=45°,
∴∠4+∠A=90°,
∴∠ACE=90°,
∴AC⊥CE,
∴AC⊥DG.
∴DG=AC,DG⊥AC.
17.(1)证明:∵CD是Rt△ABC斜边上的高,
∴∠ACB=∠ADC=90°,
∴∠A+∠ACD=∠A+∠B=90°,
∴∠ACD=∠B;
(2)解:∵AC=3,BC=4,AB=5,
∴AB CD=AC BC,
∴CD===2.4.
18.证明:∵BF是角平分线,
∴∠ABF=∠CBF,
∵AD是高线,
∵∠1=∠2=∠BED,
∴∠CBF+∠BED=90°,
∴∠ABF+∠2=90°,
∴AB⊥AC.
19.解:∠C=90°,∠EAD=90°﹣30°=60°,∠CBE=180°﹣45°=135°.
20.解:在RT△DBC中,∠D=65°,可得:∠DCB=25°,
在RT△ACE中,∠DCB=25°,可得:∠ACF=65°,
在RT△ACF中,∠ACF=65°,可得:∠EAC=25°.
21.(1)证明:∵∠AEC与∠BED是对顶角,
∴∠AEC=∠BED,
在△ACE和△BDE中,
∴△ACE≌△BDE(AAS),
∴AE=BE;
(2)解:∵∠AEC=45°,∠C=90°,
∴∠CAE=45°,
∴CE=AC=1.
22.证明:(1)在等腰Rt△BCD中,BD=CD,
∵∠BDC=90°,
∴∠BDC=∠ADC=90°,
∵在△FBD和△ACD中,
,
∴△FBD≌△ACD(SAS);
(2)∵△FBD≌△ACD,
∴∠DBF=∠DCA,
∵∠ADC=90°,
∴∠DAC+∠A=90°,
∴∠DBF+∠A=90°,
∴∠AEB=180°﹣(∠DBF+∠A)=90°,
∵BF平分∠DBC,
∴∠ABF=∠CBF,
∵在△ABE和△CBE中,
,
∴△ABE≌△CBE(ASA),
∴AB=CB,
∴△ABC是等腰三角形;
(3)∵△FBD≌△ACD,
∴BF=AC,
∵△ABE≌△CBE,
∴AE=CE=AC,
∴CE=BF;
(4)连接CG,∵在等腰Rt△BCD中,H是BC边的中点,
∴DH垂直平分BC,
∴BG=CG,
∴∠GBC=∠GCB,
∴∠EGC=∠GBC+∠GCB=2∠GBC=45°,
∴△EGC是等腰直角三角形,
∴CG=GE,
即BG=CE,
∴BG:GE=.
23.证明:(1)∵AB∥CE,
∴∠BAF=∠AEC,∠BAC+∠ACE=180°,
∵∠BAC=90°,
∴∠ACE=90°,
,∵AF⊥BD,
∴∠ABD+∠BAF=90°,∠EAC+∠BAF=90°,
∴∠ABD=∠CAE
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS)
∴BD=AE.
(2)BD与AE仍然相等,
证明:过点C作AB∥CE,过点A作AE⊥BD于点F,
∵AB∥CE,
∴∠BAE=∠AEC,∠BAC+∠ACE=180°,
∵∠BAC=90°,
∴∠ACE=90°,
,∵AF⊥BD,
∴∠ABD+∠BAF=90°,∠EAC+∠BAF=90°,
∴∠ABD=∠CAE
在△ABD和△CAE中,
∴△ABD≌△CAE(ASA)
∴BD=AE.
24.解:∵AD是△ABC的高,
∴∠BHD+∠HBD=90°,
∵BE是△ABC的高,
∴∠HBD+∠C=90°,
∴∠BHD=∠C,
∵∠C=50°,
∴∠BHD=50°.
25.解:∵∠CDF=∠OEF=90°,
∴∠C+∠AFD=90°,
∠O+∠OFE=90°,
∵∠OFE=∠CFD(对顶角相等),
∴∠O=∠C=20°.
26.证明:(1)作EM⊥AP于M,
∵∠ACB=90°,
∴∠M=∠ACD,
∵AD⊥AE,
∴∠DAE=90°,
∴∠EAM+∠AEM=90°,∠EAM+∠DAC=90°,
∴∠DAC=∠AEM,
在△ADC和△EAM中
∴△ADC≌△EAM(AAS),
∴AC=EM,
∵AC=BC,
∴BC=EM,
∵∠ACB=90°,
∴∠BCP=∠M,
在△BCP和△EMP中
∴△BCP≌△EMP(AAS),
∴BP=PE.
(2)∵△BCP≌△EMP,△ADC≌△EAM,
∴CP=PM,AM=DC,
设PC=PM=x,AC=BC=3x,AM=DC=5x,
∴BD=2x,
∴.
27.解:(1)∠ACB=90°,∠ADC=90°,
∴图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
(2)∵∠ADC=90°,
∴∠1+∠A=90°,
∵∠1+∠2=90°,
∴∠2=∠A,∠1=∠B.
28.证明:∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴∠ABD=90°,
∴AB⊥CD.
1.如图,OE平分∠AOB,且EC⊥OA,ED⊥OB,垂足分别是C、D.
(1)求证∠1=∠2;
(2)求证:OE是线段CD的垂直平分线.
2.已知在△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB,AC上的动点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)在(1)的条件下,四边形AEDF的面积是否变化,证明你的结论;
(3)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
3.如图,在△ABC中,∠ACB=90°,CD⊥AB,AF是角平分线,交CD于点E.求证:∠1=∠2.
4.如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始以每秒2cm的速度运动到B点,动点E也同时从点C开始沿射线CM方向以每秒1cm的速度运动.
(1)问动点D运动多少秒时,△ABD≌△ACE,并说明理由;
(2)设动点D运动时间为x秒,请用含x的代数式来表示△ABD的面积S;
(3)动点D运动多少秒时,△ABD与△ACE的面积比为3:1.
5.如图,在△ABC中,∠ACB=90°,CD是△ABC的一条高线,若∠B=28°.求∠ACD的度数.
6.如图,在等腰直角△ABC中∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E.若AC=10cm,求△DEB的周长.
7.如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=.现将△DEF与△ABC按如图所示的方式叠放在一起.现将△ABC保持不动,△DEF运动,且满足:点E在边BC上运动(不与B、C重合),且边DE始终经过点A,EF与AC交于M点.请问:(1)BC= ;
(2)在△DEF运动过程中,△AEM能否构成等腰三角形?若能,请求出BE的长;若不能,请说明理由.
8.在△ABC中,∠ACB﹣∠B=90°,∠BAC的角平分线交BC于E,△BAC的外角平分线交BC于F,证明:AE=AF.
9.如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=20m,CD=10m,求这块草地的面积.
10.操作:在△ABC中,AC=BC=2,∠C=90°.将一块足够大的等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①②③是旋转三角板得到的图形中的3种情况.
(1)三角板绕点P旋转,当PD⊥AC时,如图①,四边形PDCE是正方形,则PD=PE.当PD与AC不垂直时,如图②、③,PD=PE还成立吗?并选择其中的一个图形证明你的结论.
(2)若D、E两点分别在线段AC和CB上移动时,设BE的长为x,△APD的面积为y,求y与x之间的函数关系式.
(3)三角板绕点P旋转,△PEB是否能成为等腰三角形?若能,求出此时CE的长;若不能,请说明理由.
11.如图,∠A=∠C=∠BED=90°,求证:∠1=∠3,∠2=∠4.
12.(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,求∠DAE的度数;
(2)如果把第(1)题中“AB=AC”条件删去,其余条件不变,那么∠DAE的度数改变吗?试证明;
(3)如果把(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
13.如图,已知在△ABC中,∠BAC=90°,AD⊥BC于点D,E是AD上一点,试说明∠C与∠DEB的大小关系.
14.如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知∠B=48°,∠BAC=72°,求∠CAD与∠DHE的度数.
15.如图,∠C=∠D=90°,AD交BC于点E.∠CAE与∠DBE有什么关系?为什么?
16.如图1,在△ABC,∠A=45°,延长CB至D,使得BD=BC.
(1)若∠ACB=90°,求证:BD=AC;
(2)如图2,分别过点D和点C作AB所在直线的垂线,垂足分别为E、F,求证:DE=CF;
(3)如图3,若将(1)中“∠ACB=90°”改为“∠ACB=m°,并在AB延长线上取点G,使得∠1=∠A”.试探究线段AC、DG的数量与位置关系.
17.如图,CD是Rt△ABC斜边上的高.
(1)求证:∠ACD=∠B;
(2)若AC=3,BC=4,AB=5,则求CD的长.
18.如图,AD,BF分别是△ABC的高与角平分线,BF,AD交于E,∠1=∠2,求证:AB⊥AC.
19.如图,由一副三角尺拼成的图形,写出∠C,∠EAD,∠CBE的度数.
20.在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过点B作BD⊥BC,交CF的延长线于点D,若∠D=65°,求∠EAC的度数.
21.已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
(1)求证:AE=BE;
(2)若∠AEC=45°,AC=1,求CE的长.
22.如图,已知在等腰Rt△BCD中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E,H是BC边的中点,连接DH与BE相交于点G
(1)试说明:△FBD≌△ACD;
(2)试说明:△ABC是等腰三角形;
(3)试说明:CE=BF;
(4)求BG:GE的值(直接写出答案).
23.已知△ABC中,∠BAC=90°,AB=AC.
(1)如图,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
若点D在AC的延长线上,如图,其他条件同(1),请画出此时的图形,并猜想BD与AE是否仍然相等?说明你的理由.
24.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.
25.如图,已知∠CDF=∠OEF=90°,CE与OA相交于点F,若∠C=20°,求∠O的大小.
26.如图,等腰直角△ABC中,∠ACB=90°,D为CB延长线上一点,AE=AD,且AE⊥AD,BE与AC的延长线交于点P.
(1)求证:BP=PE;
(2)若AC=3PC,求的值.
27.如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
28.已知:如图,CE⊥AD,垂足为E,∠A=∠C,求证:AB⊥CD.
参考答案
1.证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴CE=DE,
∴∠1=∠2;
(2)在△OCE和△ODE中,,
∴△OCE≌△ODE(HL),
∴OC=OD,
又∵CE=DE,
∴OE是线段CD的垂直平分线.
2.(1)证明:连接AD
∵AB=AC,∠A=90°,D为BC中点
∴AD==BD=CD
且AD平分∠BAC
∴∠BAD=∠CAD=45°
在△BDE和△ADF中,
∴△BDE≌△ADF(SAS)
∴DE=DF,∠BDE=∠ADF
∵∠BDE+∠ADE=90°
∴∠ADF+∠ADE=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
(2)解:四边形AEDF面积不变.
理由:∵由(1)可知,△AFD≌△BED
∴S△BDE=S△ADF,
而S四边形AEDF=S△AED+S△ADF=S△AED+S△BDE=S△ABD
∴S四边形AEDF不会发生变化.
(3)解:仍为等腰直角三角形.
理由:∵△AFD≌△BED
∴DF=DE,∠ADF=∠BDE
∵∠ADF+∠FDB=90°
∴∠BDE+∠FDB=90°
即:∠EDF=90°
∴△EDF为等腰直角三角形.
3.证明:∵AF是角平分线,
∴∠CAF=∠BAF,
∵∠ACB=90°,CD⊥AB,
∴∠CAF+∠2=90°,∠BAF+∠AED=90°,
∴∠2=∠AED,
∵∠1=∠AED,
∴∠1=∠2.
4.解:(1)如图1,设动点D运动t秒时,△ABD≌△ACE,
由题意得:CD=2t,CE=t,则BD=6﹣2t,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵CM⊥BC,
∴∠BCM=90°,
∴∠ACE=90°﹣45°=45°,
∴∠ACE=∠B,
∴当BD=CE时,△ABD≌△ACE,
即6﹣2t=t,
t=2,
答:动点D运动2秒时,△ABD≌△ACE;
(2)如图2,过A作AF⊥BC于F,
∵AB=AC,∠BAC=90°,
∴AF是斜边的中线,
∴AF=BC=×6=3,
由题意得:CD=2x,则BD=6﹣2x,
∴S=S△ABD=BD AF=(6﹣2x)×3=﹣3x+9;
(3)设动点D运动x秒时,△ABD与△ACE的面积比为3:1,
如图2,再过A作AG⊥CM于G,
∵∠AFC=∠BCM=∠AGC=90°,
∴四边形AFCG是矩形,
∴AG=CF=BC=3,
∵△ABD与△ACE的面积比为3:1,
∴==,
∴=3,
∴BD=3CE,
即6﹣2x=3x,
5x=6,
x=,
∴动点D运动秒时,△ABD与△ACE的面积比为3:1.
5.解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD是△ABC的一条高线,
∴∠B+∠BCD=90°,
∴∠ACD=∠B=28°.
6.解:∵DE⊥AB,
∴∠C=∠AED=90°,
∵AD平分∠CAB,
∴∠CAD=∠EAD,
在△ACD和△AED中,
,
∴△ACD≌△AED(AAS),
∴AC=AE,CD=DE,
∴BD+DE=BD+CD=BC=AC=AE,
在Rt△ACB中,AB=AC=10,
∴BD+DE+BE=AE+BE=AB=10,
所以,△DEB的周长为10cm.
7.解:(1)∵△ABC是等腰直角三角形,∠BAC=90°,AB=AC=,
∴BC==2,
故答案为:2;
(2)①若AE=AM 则∠AME=∠AEM=45°,
∵∠C=45°,
∴∠AME=∠C,
又∵∠AME>∠C,
∴这种情况不成立;
②若AE=EM,
∵∠B=∠AEM=45°,
∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°,
∴∠BAE=∠MEC,
在△ABE和△ECM中,
,
∴△ABE≌△ECM(AAS),
∴CE=AB=,
∵BC=2,
∴BE=2﹣;
③若MA=ME 则∠MAE=∠AEM=45°,
∵∠BAC=90°,
∴∠BAE=45°,
∴AE平分∠BAC,
∵AB=AC,
∴BE==1.
8.证明:∵AE平分∠BAC,AF是△BAC的外角的平分线,
∴∠EAF=∠EAC+∠CAF=(∠BAC+∠CAD)=90°,
∴△EAF是直角三角形,
∵∠ACB﹣∠B=90°,
∴∠BAC=180°﹣∠ACB﹣∠B=180°﹣(90°+∠B)﹣∠B=90°﹣2∠B,
∴∠BAE=∠BAC=45°﹣∠B,
∴∠AEC=∠BAE+∠B=45°,
∴∠AFE=45°,
∴∠AEC=∠AFE,
∴AE=AF.
9.解:分别延长AD,BC交于点E.如图所示,
∵∠A=45°,∠B=∠D=90°,
∴∠DCE=∠DEB=∠A=45°,
∴AB=BE,CD=DE,
∵AB=20,CD=10,
∴BE=20,DE=10,
∵S△ABE=AB BE=200,S△CDE=CD DE=50,
∴四边形ABCD的面积=S△ABE﹣S△CDE=200﹣50=150m2.
即这块草地的面积为:150m2.
10.解:(1)PD=PE依然成立.
证明:如图②,连接PC,∵△ABC是等腰直角三角形,P是AB中点,
∴CP=PB,CP⊥AB,∠ACP=∠ACB=45°,
即∠ACP=∠B=45°,
∵∠DPC+∠CPE=∠BPE+∠CPE=90°,
∴∠DPC=∠BPE,
∴△PCD≌△PBE,
∴PD=PE.
(2)由(1)得CP⊥AB,∠ACP=∠ACB=45°,
∴△ACP是等腰直角三角形,
∴AP=CP,△PCD≌△PBE,
∴CD=BE=x,
∴AD=AC﹣CD=2﹣x,
过点P作PF⊥AC于点F,则PF=AC=1,
∴△APD的面积y=AD PF=(2﹣x)×1,
即y=1﹣x.
(3)分三种情况讨论如下:
①当PE=PB时,点C与点E重合,即CE=0.
②当PE=BE时,CE=1.
③当BE=PB时,
若点E在线段CB上时,CE=2﹣;
若点E在CB延长线上时CE=2+.
11.证明:∵∠BED=90°,
∴∠1+∠2=180°﹣90°=90°,
∵∠A=90°,
∴∠2+∠3=90°,
∴∠1=∠3;
同理可得∠2=∠4.
12.解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=(180°﹣∠B)=67.5°,
∵CE=CA,
∴∠CAE=∠E=∠ACB=22.5°,
在△ABE中,∠BAE=180°﹣∠B﹣∠E=112.5°,
∴∠DAE=∠BAE﹣∠BAD=112.5°﹣67.5°=45度;
(2)不改变.
设∠CAE=x,
∵CA=CE,
∴∠E=∠CAE=x,
∴∠ACB=∠CAE+∠E=2x,
在△ABC中,∠BAC=90°,
∴∠B=90°﹣∠ACB=90°﹣2x,
∵BD=BA,
∴∠BAD=∠BDA=(180°﹣∠B)=x+45°,
在△ABE中,∠BAE=180°﹣∠B﹣∠E,
=180°﹣(90°﹣2x)﹣x=90°+x,
∴∠DAE=∠BAE﹣∠BAD,
=(90°+x)﹣(x+45°)=45°;
(3)∠DAE=∠BAC.
理由:设∠CAE=x,∠BAD=y,
则∠B=180°﹣2y,∠E=∠CAE=x,
∴∠BAE=180°﹣∠B﹣∠E=2y﹣x,
∴∠DAE=∠BAE﹣∠BAD=2y﹣x﹣y=y﹣x,
∠BAC=∠BAE﹣∠CAE=2y﹣x﹣x=2y﹣2x,
∴∠DAE=∠BAC.
13.答:∠C<∠DEB.
证明:∵∠BAC=90°,∴∠BAE+∠CAE=90°,
∵AD⊥BC,∴∠C+∠CAE=90°,
∴∠C=∠BAE,
∵∠BAE<∠DEB,
∴∠C<∠DEB.
14.解:∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣48°=42°,
∴∠CAD=∠BAC﹣∠BAD=30°,
∵CE⊥AB,
∴∠AEC=90°,
由三角形的外角性质得,∠DHE=∠BAD+∠AEH=42°+90°=132°.
15.解:∠CAE与∠DBE相等.
理由如下:∵在△CAE,△DBE中,∠C=∠D=90°,∠CEA=∠DEB,
∴∠CAE=90°﹣∠CEA,∠DBE=90°﹣∠DEB,
即∠CAE=∠DBE.
16.(1)证明:∵∠A=45°,∠ACB=90°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵BD=BC,
∴BD=AC;
(2)证明:∵DE⊥AB,CF⊥AB,
∴∠E=∠CFB=90°,
在△DBE与△CBF中,
∵,
∴△DBE≌△CBF(AAS),
∴DE=CF;
(3)解:DG=AC,DG⊥AC.
证明:过点C作CE∥DG交AB于点E,
∴∠2=∠3,
∵∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠4,
∵∠1=∠A,
∴∠4=∠A,
∴AC=CE,
在△DBG与△CBE中,
∵,
∴△DBG≌△CBE(AAS),
∴CE=DG,
∴DG=AC.
∵∠A=45°,
∴∠4+∠A=90°,
∴∠ACE=90°,
∴AC⊥CE,
∴AC⊥DG.
∴DG=AC,DG⊥AC.
17.(1)证明:∵CD是Rt△ABC斜边上的高,
∴∠ACB=∠ADC=90°,
∴∠A+∠ACD=∠A+∠B=90°,
∴∠ACD=∠B;
(2)解:∵AC=3,BC=4,AB=5,
∴AB CD=AC BC,
∴CD===2.4.
18.证明:∵BF是角平分线,
∴∠ABF=∠CBF,
∵AD是高线,
∵∠1=∠2=∠BED,
∴∠CBF+∠BED=90°,
∴∠ABF+∠2=90°,
∴AB⊥AC.
19.解:∠C=90°,∠EAD=90°﹣30°=60°,∠CBE=180°﹣45°=135°.
20.解:在RT△DBC中,∠D=65°,可得:∠DCB=25°,
在RT△ACE中,∠DCB=25°,可得:∠ACF=65°,
在RT△ACF中,∠ACF=65°,可得:∠EAC=25°.
21.(1)证明:∵∠AEC与∠BED是对顶角,
∴∠AEC=∠BED,
在△ACE和△BDE中,
∴△ACE≌△BDE(AAS),
∴AE=BE;
(2)解:∵∠AEC=45°,∠C=90°,
∴∠CAE=45°,
∴CE=AC=1.
22.证明:(1)在等腰Rt△BCD中,BD=CD,
∵∠BDC=90°,
∴∠BDC=∠ADC=90°,
∵在△FBD和△ACD中,
,
∴△FBD≌△ACD(SAS);
(2)∵△FBD≌△ACD,
∴∠DBF=∠DCA,
∵∠ADC=90°,
∴∠DAC+∠A=90°,
∴∠DBF+∠A=90°,
∴∠AEB=180°﹣(∠DBF+∠A)=90°,
∵BF平分∠DBC,
∴∠ABF=∠CBF,
∵在△ABE和△CBE中,
,
∴△ABE≌△CBE(ASA),
∴AB=CB,
∴△ABC是等腰三角形;
(3)∵△FBD≌△ACD,
∴BF=AC,
∵△ABE≌△CBE,
∴AE=CE=AC,
∴CE=BF;
(4)连接CG,∵在等腰Rt△BCD中,H是BC边的中点,
∴DH垂直平分BC,
∴BG=CG,
∴∠GBC=∠GCB,
∴∠EGC=∠GBC+∠GCB=2∠GBC=45°,
∴△EGC是等腰直角三角形,
∴CG=GE,
即BG=CE,
∴BG:GE=.
23.证明:(1)∵AB∥CE,
∴∠BAF=∠AEC,∠BAC+∠ACE=180°,
∵∠BAC=90°,
∴∠ACE=90°,
,∵AF⊥BD,
∴∠ABD+∠BAF=90°,∠EAC+∠BAF=90°,
∴∠ABD=∠CAE
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS)
∴BD=AE.
(2)BD与AE仍然相等,
证明:过点C作AB∥CE,过点A作AE⊥BD于点F,
∵AB∥CE,
∴∠BAE=∠AEC,∠BAC+∠ACE=180°,
∵∠BAC=90°,
∴∠ACE=90°,
,∵AF⊥BD,
∴∠ABD+∠BAF=90°,∠EAC+∠BAF=90°,
∴∠ABD=∠CAE
在△ABD和△CAE中,
∴△ABD≌△CAE(ASA)
∴BD=AE.
24.解:∵AD是△ABC的高,
∴∠BHD+∠HBD=90°,
∵BE是△ABC的高,
∴∠HBD+∠C=90°,
∴∠BHD=∠C,
∵∠C=50°,
∴∠BHD=50°.
25.解:∵∠CDF=∠OEF=90°,
∴∠C+∠AFD=90°,
∠O+∠OFE=90°,
∵∠OFE=∠CFD(对顶角相等),
∴∠O=∠C=20°.
26.证明:(1)作EM⊥AP于M,
∵∠ACB=90°,
∴∠M=∠ACD,
∵AD⊥AE,
∴∠DAE=90°,
∴∠EAM+∠AEM=90°,∠EAM+∠DAC=90°,
∴∠DAC=∠AEM,
在△ADC和△EAM中
∴△ADC≌△EAM(AAS),
∴AC=EM,
∵AC=BC,
∴BC=EM,
∵∠ACB=90°,
∴∠BCP=∠M,
在△BCP和△EMP中
∴△BCP≌△EMP(AAS),
∴BP=PE.
(2)∵△BCP≌△EMP,△ADC≌△EAM,
∴CP=PM,AM=DC,
设PC=PM=x,AC=BC=3x,AM=DC=5x,
∴BD=2x,
∴.
27.解:(1)∠ACB=90°,∠ADC=90°,
∴图中有3个直角三角形,分别是△ACD,△BCD,△ABC.
(2)∵∠ADC=90°,
∴∠1+∠A=90°,
∵∠1+∠2=90°,
∴∠2=∠A,∠1=∠B.
28.证明:∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴∠ABD=90°,
∴AB⊥CD.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
