2021-2022学年数学人教版九年级下册26.1反比例函数 同步课时作业(word解析版)
文档属性
| 名称 | 2021-2022学年数学人教版九年级下册26.1反比例函数 同步课时作业(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 339.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 18:29:38 | ||
图片预览


文档简介
26.1反比例函数—2021-2022学年数学人教版
九年级下册同步课时作业
1.已知反比例函数的解析式为,则a的取值范围是( )
A. B. C. D.
2.关于正比例函数和反比例函数的说法正确的是( )
A.自变量x的指数相同 B.比例系数相同
C.自变量x的取值范围相同 D.函数值y的取值范围相同
3.已知y是关于x的反比例函数,且当时,,则y关于x的函数表达式为( )
A. B. C. D.
4.如果反比例函数的图象经过点,那么函数的图象应在( )
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第三、四象限
5.当时,下列函数是反比例函数的是( )
A. B. C. D.
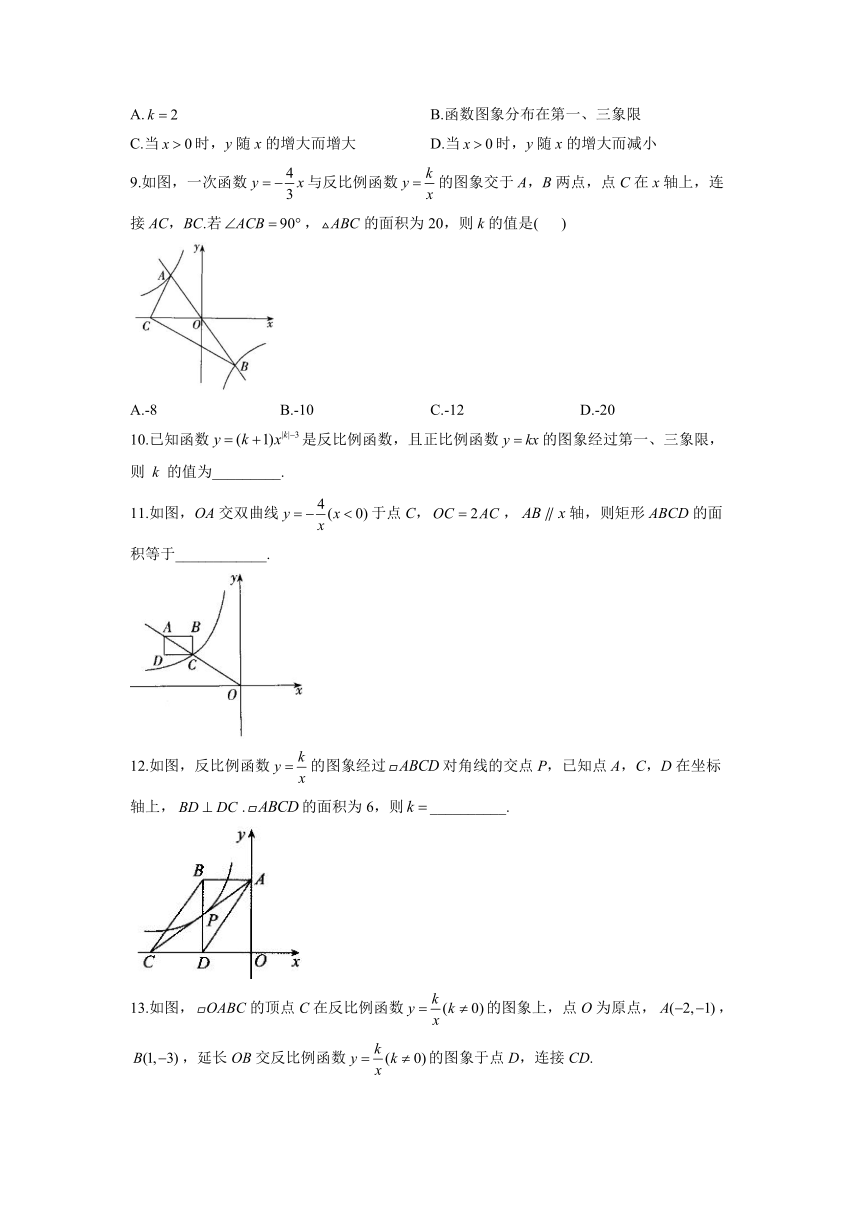
6.如图,点A在反比例函数的图象上,过点A作轴,垂足为点B,点C在y轴上,则的面积为( )
A.3 B.2 C. D.1
7.若点、、都在反比例函数的图象上,则、、的大小关系是( )
A. B. C. D.
8.反比例函数的图象经过点,则下列说法错误的是( )
A. B.函数图象分布在第一、三象限
C.当时,y随x的增大而增大 D.当时,y随x的增大而减小
9.如图,一次函数与反比例函数的图象交于A,B两点,点C在x轴上,连接AC,BC.若,的面积为20,则k的值是( )
A.-8 B.-10 C.-12 D.-20
10.已知函数是反比例函数,且正比例函数的图象经过第一、三象限,则的值为_________.
11.如图,OA交双曲线于点C,,轴,则矩形ABCD的面积等于____________.
12.如图,反比例函数的图象经过对角线的交点P,已知点A,C,D在坐标
轴上,.的面积为6,则__________.
13.如图,的顶点C在反比例函数的图象上,点O为原点,,,延长OB交反比例函数的图象于点D,连接CD.
(1)求反比例函数的表达式;
(2)求点D的坐标;
(3)试计算的面积.
答案以及解析
1.答案:C
解析:由题意,得,解得.
2.答案:B
解析:两个函数的比例系数都是.故选B.
3.答案:B
解析:设y关于x的函数表达式为(k是常数,),将,代入,得,解得.所以该函数表达式是.故选B.
4.答案:C
解析:反比例函数的图象经过点,.函数的图象在第二、四象限.故选C.
5.答案:C
解析:A中,当时,,此时不是反比例函数;B中,当时,,,,此时不是反比例函数;C中,当时,函数为,是反比例函数;D中,当时,函数为,不是反比例函数.故选C.
6.答案:C
解析:连接OA,如图.
轴,..
而,.故选C.
7.答案:C
解析:点、、都在反比例函数的图象上,,,,,.故选C.
8.答案:C
解析:反比例函数的图象经过点,,解得,故选项A说法正确;,该函数的图象在第一、三象限,故选项B说法正确;当时,y随x的增大而减小,故选项C说法错误、选项D说法正确.故选C.
9.答案:C
解析:设点A的坐标为,则,.由题意可得,.,..解得,,.点A的坐标为..故选C.
10.答案:2
解析:是反比例函数,且正比例函数的图象经过第一、三象限,解得.
11.答案:1
解析:OA交双曲线于点C,,设点C的坐标为,则点A的坐标为,,.,,矩形ABCD的面积.
12.答案:-3
解析:过点P作轴于点E.四边形ABCD为平行四边形,,又轴,ABDO为矩形,,.P为对角线交点,轴,四边形PDOE为矩形,面积为3,即.设P点坐标为,.
13.答案:(1)如图,过点C,D分别作x轴的垂线,垂足分别为E,F.
的顶点O为原点,,,
点C的坐标为..
反比例函数的表达式为.
(2)设OB的表达式为,
将代入,得.
OB的表达式为.
联立与,得.
解得或(舍去).
将代入,得.
点D的坐标为.
(3)点C,D都在反比例函数的图象上,
的面积的面积.
的面积的面积+梯形DFEC的面积的面积
=梯形DFEC的面积.
九年级下册同步课时作业
1.已知反比例函数的解析式为,则a的取值范围是( )
A. B. C. D.
2.关于正比例函数和反比例函数的说法正确的是( )
A.自变量x的指数相同 B.比例系数相同
C.自变量x的取值范围相同 D.函数值y的取值范围相同
3.已知y是关于x的反比例函数,且当时,,则y关于x的函数表达式为( )
A. B. C. D.
4.如果反比例函数的图象经过点,那么函数的图象应在( )
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第三、四象限
5.当时,下列函数是反比例函数的是( )
A. B. C. D.
6.如图,点A在反比例函数的图象上,过点A作轴,垂足为点B,点C在y轴上,则的面积为( )
A.3 B.2 C. D.1
7.若点、、都在反比例函数的图象上,则、、的大小关系是( )
A. B. C. D.
8.反比例函数的图象经过点,则下列说法错误的是( )
A. B.函数图象分布在第一、三象限
C.当时,y随x的增大而增大 D.当时,y随x的增大而减小
9.如图,一次函数与反比例函数的图象交于A,B两点,点C在x轴上,连接AC,BC.若,的面积为20,则k的值是( )
A.-8 B.-10 C.-12 D.-20
10.已知函数是反比例函数,且正比例函数的图象经过第一、三象限,则的值为_________.
11.如图,OA交双曲线于点C,,轴,则矩形ABCD的面积等于____________.
12.如图,反比例函数的图象经过对角线的交点P,已知点A,C,D在坐标
轴上,.的面积为6,则__________.
13.如图,的顶点C在反比例函数的图象上,点O为原点,,,延长OB交反比例函数的图象于点D,连接CD.
(1)求反比例函数的表达式;
(2)求点D的坐标;
(3)试计算的面积.
答案以及解析
1.答案:C
解析:由题意,得,解得.
2.答案:B
解析:两个函数的比例系数都是.故选B.
3.答案:B
解析:设y关于x的函数表达式为(k是常数,),将,代入,得,解得.所以该函数表达式是.故选B.
4.答案:C
解析:反比例函数的图象经过点,.函数的图象在第二、四象限.故选C.
5.答案:C
解析:A中,当时,,此时不是反比例函数;B中,当时,,,,此时不是反比例函数;C中,当时,函数为,是反比例函数;D中,当时,函数为,不是反比例函数.故选C.
6.答案:C
解析:连接OA,如图.
轴,..
而,.故选C.
7.答案:C
解析:点、、都在反比例函数的图象上,,,,,.故选C.
8.答案:C
解析:反比例函数的图象经过点,,解得,故选项A说法正确;,该函数的图象在第一、三象限,故选项B说法正确;当时,y随x的增大而减小,故选项C说法错误、选项D说法正确.故选C.
9.答案:C
解析:设点A的坐标为,则,.由题意可得,.,..解得,,.点A的坐标为..故选C.
10.答案:2
解析:是反比例函数,且正比例函数的图象经过第一、三象限,解得.
11.答案:1
解析:OA交双曲线于点C,,设点C的坐标为,则点A的坐标为,,.,,矩形ABCD的面积.
12.答案:-3
解析:过点P作轴于点E.四边形ABCD为平行四边形,,又轴,ABDO为矩形,,.P为对角线交点,轴,四边形PDOE为矩形,面积为3,即.设P点坐标为,.
13.答案:(1)如图,过点C,D分别作x轴的垂线,垂足分别为E,F.
的顶点O为原点,,,
点C的坐标为..
反比例函数的表达式为.
(2)设OB的表达式为,
将代入,得.
OB的表达式为.
联立与,得.
解得或(舍去).
将代入,得.
点D的坐标为.
(3)点C,D都在反比例函数的图象上,
的面积的面积.
的面积的面积+梯形DFEC的面积的面积
=梯形DFEC的面积.
