2021-2022学年北师大版数学九年级下册第3章 圆 综合练习卷(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册第3章 圆 综合练习卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 662.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 19:25:40 | ||
图片预览


文档简介
2021北师大版九下圆综合练习卷
一、单选题
1.(2021·杨浦模拟)在平面直角坐标系中,以点 为圆心,1为半径的圆与 轴的位置关系是( )
A. 相离 B. 相切 C. 相交 D. 不确定
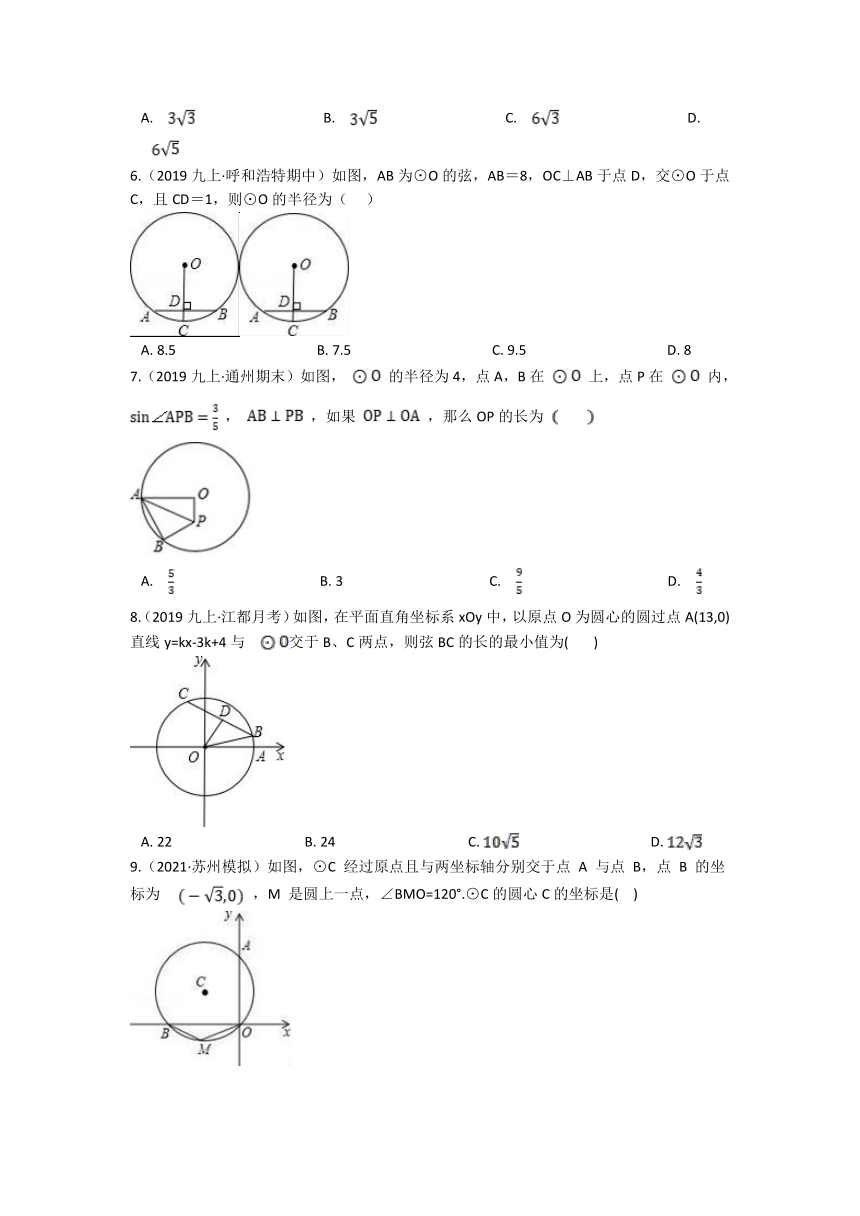
2.(2020九上·泗阳期中)如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°.则∠BOC等于( )
A. 125° B. 120° C. 115° D. 100°
3.(2019九上·白云期中)如图,OA、OB是⊙O的半径,点C在⊙O上,连接AC、BC , 若∠A=20°,∠B=70°,则∠ACB的度数为( )
A. 50° B. 55° C. 60° D. 65°
4.(2019九上·呼兰期中)如图,四边形 为 的内接四边形,若 ,则 的度数是( )
A. B. C. D.
5.(2020·白云模拟)如图,已知等边 的内切圆 半径为3,则 的长为 ( )
A. B. C. D.
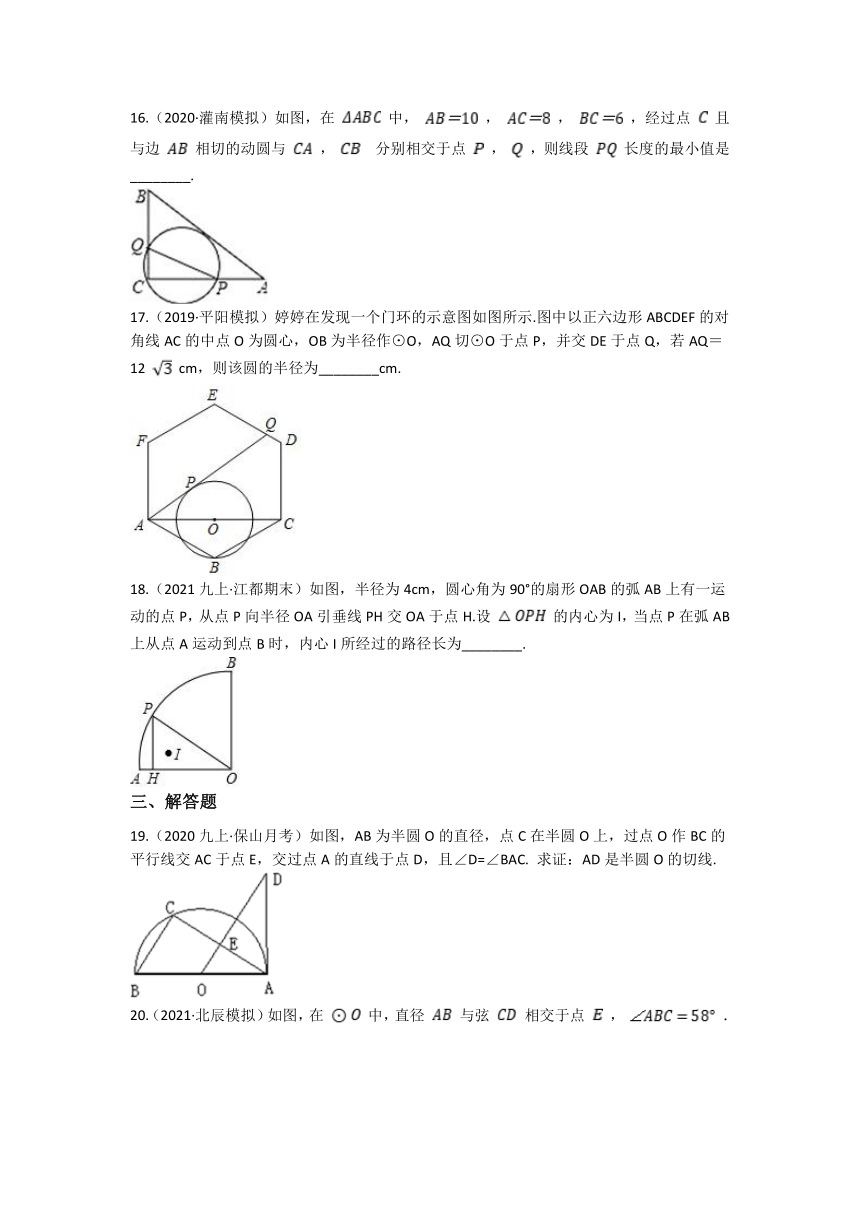
6.(2019九上·呼和浩特期中)如图,AB为⊙O的弦,AB=8,OC⊥AB于点D,交⊙O于点C,且CD=1,则⊙O的半径为( )
A. 8.5 B. 7.5 C. 9.5 D. 8
7.(2019九上·通州期末)如图, 的半径为4,点A,B在 上,点P在 内, , ,如果 ,那么OP的长为
A. B. 3 C. D.
8.(2019九上·江都月考)如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( )
A. 22 B. 24 C. D.
9.(2021·苏州模拟)如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为 ,M 是圆上一点,∠BMO=120°.⊙C的圆心C的坐标是( )
A. B. C. D.
10.(2021·重庆模拟)如图, 是 的直径, 为 的弦,且 于点 ,点 为圆上一点,若 , , ,则 的长为( )
A. B. C. 4 D. 5
二、填空题
11.(2020九上·泰州月考)已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是________.
12.(2019·云南模拟)如果圆锥的侧面展开图的扇形半径是6,弧长是4π,那么这个扇形的圆心角为________.
13.(2020九上·河北期中)以 为中心点的量角器与直角三角板 如图所示摆放,直角顶点 在零刻度线所在直线 上,且量角器与三角板只有一个公共点 ,若点 的读数为135°,则 的度数是________.
14.(2019九上·滨湖期末)如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=65°,则∠ACD=________°.
15.(2020九上·龙凤期末)已知 的半径为 ,直线 与 相交,则圆心 到直线 距离 的取值范围是 .
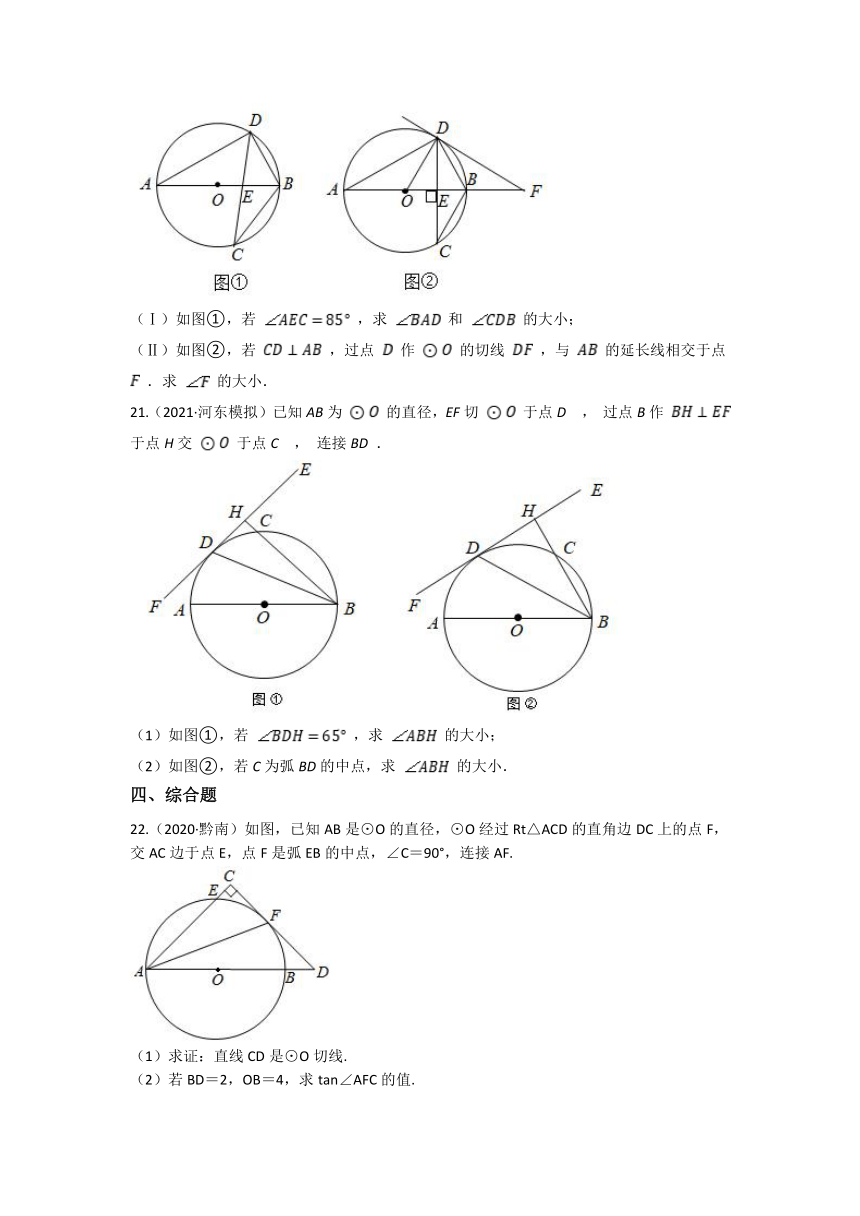
16.(2020·灌南模拟)如图,在 中, , , ,经过点 且与边 相切的动圆与 , 分别相交于点 , ,则线段 长度的最小值是________.
17.(2019·平阳模拟)婷婷在发现一个门环的示意图如图所示.图中以正六边形ABCDEF的对角线AC的中点O为圆心,OB为半径作⊙O,AQ切⊙O于点P,并交DE于点Q,若AQ=12 cm,则该圆的半径为________cm.
18.(2021九上·江都期末)如图,半径为4cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设 的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为________.
三、解答题
19.(2020九上·保山月考)如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC. 求证:AD是半圆O的切线.
20.(2021·北辰模拟)如图,在 中,直径 与弦 相交于点 , .
(Ⅰ)如图①,若 ,求 和 的大小;
(Ⅱ)如图②,若 ,过点 作 的切线 ,与 的延长线相交于点 .求 的大小.
21.(2021·河东模拟)已知AB为 的直径,EF切 于点D , 过点B作 于点H交 于点C , 连接BD .
(1)如图①,若 ,求 的大小;
(2)如图②,若C为弧BD的中点,求 的大小.
四、综合题
22.(2020·黔南)如图,已知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F,交AC边于点E,点F是弧EB的中点,∠C=90°,连接AF.
(1)求证:直线CD是⊙O切线.
(2)若BD=2,OB=4,求tan∠AFC的值.
23.(2019九上·诸暨月考)如图,⊙O的直径AB=20,P是AB上(不与点A,B重合)的任一点,点C,D为⊙O上的两点,若∠APD=∠BPC,则称∠DPC为直径AB的“回旋角”,利用圆的对称性可知:“回旋角”∠DPC的度数与弧CD的度数相等.
(1)若∠DPC为直径AB的“回旋角”,且∠DPC=100°,求∠APD的大小;
(2)若直径AB的“回旋角”为90°,且△PCD的周长为 ,求AP的长.
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】解:∵点A(2,1)到x轴的距离为1,圆的半径=1,
∴点A(2,1)到x轴的距离=圆的半径,
∴圆与x轴相切;
故答案为:B.
【分析】利用点到直线的距离跟半径大小进行比较即可判断直线和圆的位置关系。
2.【答案】 C
【解析】【解答】解: ⊙O是△ABC的内切圆
∴BO、CO分别平分∠ABC、∠ACB
又 ∠ABC=50°,∠ACB=80°
∴ =25°、 °
∴ 180° =115°
故答案为:C.
【分析】根据 ⊙O是三角形△ABC的内切圆,知BO、CO是三角形的角平分线,从而求出 ∠OBC及∠OCB的度数,利用三角形内角和定理,便可找到答案.
3.【答案】 A
【解析】【解答】连接OC,∵OA=OC,∴∠OCA=∠A=20°,∵OC=OB,∴∠OCB=∠B=70°,∴∠ACB=∠OCB-∠OCA=70°-20°=50°,
故答案为:A.
【分析】连接OC,根据OA=OC,得出∠OCA=∠A=20°,再根据OC=OB,得出∠OCB=∠B=70°,即可求出∠ACB=∠OCB-∠OCA=50°.
4.【答案】 D
【解析】【解答】解:∵四边形 为 的内接四边形, ,
∴∠ABC=70°,
∴∠AOC=2∠ABC=140°,
故答案为:D.
【分析】先根据圆内接四边形的性质得到∠ABC的度数,再根据圆心角等于同弧所对圆周角的2倍即可得到答案.
5.【答案】 C
【解析】【解答】解:连接OB、OD.
∵△ABC是等边三角形,
∴∠ABC=60°,
∵⊙o为等边△ABC的内切圆,
∴∠OBD=∠ABC=30°,OD⊥AB,BD=AD,
∴OB=2OD=6,
∴BD==3 ,
∴AB=6.
故答案为:C.
【分析】连接OB、OD,根据圆内切三角形的性质可得∠OBD、∠ODB的度数及BD=AD,然后利用勾股定理计算出BD的长,即可得到AB的长.
6.【答案】 A
【解析】【解答】解:如图所示:连接 ,则 长为半径.
∵ 于点 ,
∴ ,
∵在 中, ,
∴ ,
∴ ,
故答案为A.
【分析】根据垂径定理得到直角三角形,求出 的长,连接 ,得到直角三角形,然后在直角三角形中计算出半径的长.
7.【答案】 D
【解析】【解答】解:如图,连接OB,作 交OP的延长线于M,作 交MB的延长线于 则四边形AOMN是矩形,
,
、O、P、B四点共圆,
,
,
,
,设 , ,
在 中, ,
解得 负根已经舍弃 ,
, , ,
, ,
,
,
∽ ,
,
,
,
.
故答案为:D.
【分析】如图,连接OB,作 交OP的延长线于M,作 交MB的延长线于 则四边形AOMN是矩形,推出A、O、P、B四点共圆,根据圆周角定理得到 ,根据三角函数的定义设 , ,根据勾股定理得到 负根已经舍弃 ,根据相似三角形的性质即可得到结论.
8.【答案】 B
【解析】【解答】根据题意可得直线经过定点D(3,4),则OD=5,当OD⊥BC时,BC取得最小值,根据垂径定理可得BC=24.
【分析】根据直线经过定点D(3,4),求出最短的弦BC是过点D且该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心过点A(13,0 ),求出OB的长,然后利用勾股定理求出BD即可.
9.【答案】 C
【解析】【解答】解:连接 AB,OC,
∵∠AOB=90°,
∴AB为⊙C的直径,
∵∠BMO=120°,
∴∠BAO=60°,
∴∠BCO=2∠BAO=120°,
过 C 作 CD⊥OB 于 D,则 OD= OB,∠DCB=∠DCO=60°,
∵B(﹣ ,0),,
∴BD=OD= .
在 Rt△COD 中.CD=OD tan30°= ,
∴C(﹣ , ),
故答案为:C
【分析】 连接 AB,OC,利用圆周角定理可证得AB是圆O的直径,利用圆内接四边形的性质可求出∠BAO=60°,利用圆周角定理可求出∠BCO的度数;过 C 作 CD⊥OB 于 D,利用垂径定理,由点B的坐标,可求出OD的长;再利用解直角三角形求出CD的长;即可得到点C的坐标.
10.【答案】 A
【解析】【解答】解:如图,连接 交 于 ,设 交 于 ,过点 作 于 .
,
,
,
,
,
,
, ,
,
,
,
是直径,
,
,
,
,
,
,
, ,
,
,
,
,
, ,
,
,
,
,
,
,
,
,
, ,
,
,
故答案为:A.
【分析】连接 交 于 ,设 交 于 ,过点 作 于 ,由垂径定理和等量代换易得 , 由垂径定理推论可得 , 易得 , 即可得AE=CJ,由直径所对的圆周角是直角可得∠F=∠CJT=90°,易得 , 得BT=CT,易证 , 由等量代换和勾股定理可得结果.
二、填空题
11.【答案】
【解析】【解答】解: 四边形ABCD内接于⊙O,
∴∠ABC+∠ADC=
又∵∠ABC=70°
∴∠ADC= -∠ABC= - =
故答案为: .
【分析】根据圆内接四边形的对角互补即可得到答案.
12.【答案】 120°
【解析】【解答】设这个扇形的圆心角为n°,
则 =4π,
解得,n=120,
故答案为:120°.
【分析】根据弧长公式和已知条件可得 , 解方程可求解。
13.【答案】 45
【解析】【解答】解:∵AB是⊙O的切线,
∴∠OPB=90°,
∵∠ABC=90°,
∴OP∥BC ,
∵点 的读数为135°,
∴∠EOP=135°
∴∠POB=180°-135°=45°
∴∠CBD=∠POB=45°,
故答案为:45.
【分析】根据切线的性质,求出∠OPB=90°,证明得到OP∥BC,根据平行线的性质即可得到∠POB=∠CBD,得到答案即可。
14.【答案】 40
【解析】【解答】∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,∠ACB=90°,
∴∠ADC=180°﹣∠ABC=115°,∠BAC=90°﹣∠ABC=25°,
∵过点C的切线与边AD所在直线垂直于点M,
∴∠MCA=∠ABC=65°,∠AMC=90°,
∵∠ADC=∠AMC+∠DCM,
∴∠DCM=∠ADC﹣∠AMC=25°,
∴∠ACD=∠MCA﹣∠DCM=65°﹣25°=40°,
故答案为:40.
【分析】由圆内接四边形的性质求出∠ADC=180°-∠ABC=115°,由圆周角定理求出∠ACB=90°,得出∠BAC=25°,由过点C的切线与边AD所在直线垂直于点M,可得∠MCA=∠ABC=65°,∠AMC=90°,继而根据三角形的外角性质得出∠DCM=∠ADC-∠AMC=25°,即可求出∠ACD的度数.
15.【答案】
【解析】【解答】∵⊙O的半径为5,直线AB与⊙O相交,
∴圆心到直线AB的距离小于圆的半径,
即0≤d<5;
故答案为:0≤d<5.
【分析】根据直线AB和圆相交,则圆心到直线的距离小于圆的半径即可得到问题答案。
16.【答案】
【解析】【解答】解:设圆心为F, 与 的切点为 ,
, , ,
是 的直径,
连接 ,连接 , ,
∵点 、 在 上, 是 的直径
,
又∵
∴ ,
∵ 与 切于点 ,
∴ ;
∴当点 是 的斜边 的高的中点时, 三点共线,且 为 的斜边 的高,此时 的直径等于
又∵ ,
∴ 能取到最小值4.8.
故答案为:
【分析】设圆心为F,圆F与AB的切点为D,连接FD、CF、CD,则有 ;由勾股定理的逆定理知, 是直角三角形,直径 ,由线段最短知 ,即 ,只有当点F在CD上,且CD是直角三角形ABC的斜边AB的高上CD时, 有最小值为CD的长,由直角三角形的面积公式知,此时 .
17.【答案】
【解析】【解答】解:连接OB,OP,
∵AB=BC,O为AC的中点,
∴OB⊥AC,
∵AQ是⊙O的切线,
∴OP⊥AQ,
设该圆的半径为r,
∴OB=OP=r,
∵∠ABC=120°,
∴∠BAO=30°,
∴AB=BC=CD=2r,AO= ,
∴AC= ,
∴sin∠PAO= ,
过Q作QG⊥AC于G,过D作DH⊥QG于H,
则四边形DHGC是矩形,
∴HG=CD,DH=CG,∠HDC=90°,
∴sin∠PAO= ,∠QDH=120°﹣90°=30°,
∴QG=12,
∴AG= ,
∴QH=12﹣2r,DH= ,
∴tan∠QDH=tan30°= ,
解得r= ,
∴该圆的半径为 cm,
故答案为: .
【分析】连接OB,OP,设该圆的半径为r,根据等腰三角形的三线合一得出OB⊥AC,根据切线的性质得出OP⊥AQ,设该圆的半径为r,根据正六边形的性质得出∠ABC=120°,根据三角形的内角和及等边对等角得出∠BAO=30°,根据含30°直角三角形的性质得出AB=BC=CD=2r,AO= ,故AC= ,过Q作QG⊥AC于G,过D作DH⊥QG于H,则四边形DHGC是矩形,根据矩形的性质得出HG=CD,DH=CG,∠HDC=90°,根据正弦函数的定义,由sin∠PAO= 算出QG的长,进而根据tan∠QDH= 即可求出r的长得出答案。
18.【答案】
【解析】【解答】解:如图,连OI,PI,AI,
∵△OPH的内心为I,
∴∠IOP=∠IOA,∠IPO=∠IPH,
∴∠PIO= -∠IPO-∠IOP= - (∠HOP+∠OPH),
而PH⊥OA,即∠PHO= ,
∴∠PIO= - (∠HOP+∠OPH)= - ( - )= ,
又∵OP=OA,OI公共,
而∠IOP=∠IOA,
∴△OPI≌△OAI,
∴∠AIO=∠PIO= ,
所以点I在以OA为弦,并且所对的圆周角为 的一段劣弧上;
过A、I、O三点作⊙O′,如图,连O′A,O′O,
在优弧AO上取点P,连PA,PO,
∵∠AIO= ,
∴∠APO= - = ,
∴∠A O= ,而OA=4cm,
∴∠AO = ,
∴O′O= OA= ×4=2 ,
∴弧OA的长= (cm),
所以内心I所经过的路径长为 cm.
故答案为: cm..
【分析】如图,连OI,PI,AI,由△OPH的内心为I,可得到∠PIO= -∠IPO-∠IOP= - (∠HOP+∠OPH)= ,并且易证△OPI≌△OAI,得到∠AIO=∠PIO= ,所以点I在以OA为弦,并且所对的圆周角为 的一段劣弧上;过A、I、O三点作⊙O′,如图,连O′A,O′O,在优弧AO上取点P,连PA,PO,可得∠APO= - = ,得∠A O= , OA= ×4=2 ,然后利用弧长公式计算弧OA的长.
三、解答题
19.【答案】 解:∵AB为半圆O的直径,
∴∠BCA=90°,
又∵BC∥OD,
∴∠OEA=90°,即OD⊥AC,
∴∠D+∠DAE=90°,
∵∠D=∠BAC,
∴∠BAC+∠DAE=90°,即∠DAB=90°,
∴OA⊥AD,
∴AD是半圆O的切线.
【解析】【分析】根据圆的性质及平行线的性质证得OD⊥AC,从而得到∠D+∠DAE=90°,再进行等量代换即可证明结论.
20.【答案】 解:(Ⅰ)∵ ,
∴∠C=
∴
∵直径 与弦 相交于点 ,
∴∠ADB=90°,
又∵
∴
(Ⅱ)∵
∴∠AEC=90°
又∵
∴
∴
∵ 是 的切线
∴
∴
【解析】【分析】(Ⅰ)先求出 ,再求出 ∠ADB=90°, 最后计算求解即可;
(Ⅱ)先求出 ∠AEC=90° ,再求出 ,最后计算求解即可。
21.【答案】 (1)如图,连接OD.
由切线的性质结合题意可知 ,
∴ ,
∴ .
∵ ,
∴ .
∵ ,
∴ ,
∴ .
∴ .
(2)如图,连接OD、OC、CD.
∵OC=OD,
∴ .
∵ ,即 ,
∴ ,
∵ ,
∴ .
∵C为 中点,
∴ ,
由(1)可知 ,
∴ ,
∵ ,
∴ .
∴ .
【解析】【分析】(1)先求出 ,再求出 ,最后计算求解即可;
(2)先求出 , 再求出 ,最后计算求解即可。
四、综合题
22.【答案】 (1)证明:连结OF,BE,如图:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵∠C=90°,
∴∠AEB=∠ACD,
∴BE∥CD,
∵点F是弧BE的中点,
∴OF⊥BE,
∴OF⊥CD,
∵OF为半径,
∴直线DF是⊙O的切线;
(2)解:∵∠C=∠OFD=90°,
∴AC∥OF,
∴△OFD∽△ACD,
∴ = ,
∵BD=2,OF=OB=4,
∴OD=6,AD=10,
∴AC= = = ,
∴CD= = = ,
∵AC∥OF,OA=4,
∴ = ,即 = ,
解得:CF= ,
∴tan∠AFC= = = .
【解析】【分析】(1)连结OF,BE,得到BE∥CD,根据根据垂径定理及平行线的性质得到CD⊥OF,即可得出结论;
(2)首先判断出 △OFD∽△ACD ,由相似三角形的性质求出AC长,再由勾股定理可求得DC长,进而根据平行线分线段成比例能求出CF长,最后根据正切函数的定义即可得出结果.
23.【答案】 (1)解:∵ ∠DPC为直径AB的“回旋角”,且∠DPC=100°, 由题意得: ∠APD=∠BPC =(180°-100)÷2=40°.
(2)解:延长DP交圆于F点,连接CF,过O作OH⊥FD,∵ ∠APD=∠BPC=(180°-90°)÷2=45°,∵∠APD=∠BPF, ∴ ∠FPB=∠BPC,则由圆的对称性知,PC=PF,∴FD=PC+PD,由题中定义可知, ∠DPC = ∠DOC=90°,∴DC=OC=10 , ∴FD=PD+PC=16+10-10=16,∵DH=FD=8,∵OH= , ∴PO==6 , ∴AP=OA-OP=10-6.当A、B对调时,即P在OB之间时,AP=OA+OP=10+6.
一、单选题
1.(2021·杨浦模拟)在平面直角坐标系中,以点 为圆心,1为半径的圆与 轴的位置关系是( )
A. 相离 B. 相切 C. 相交 D. 不确定
2.(2020九上·泗阳期中)如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°.则∠BOC等于( )
A. 125° B. 120° C. 115° D. 100°
3.(2019九上·白云期中)如图,OA、OB是⊙O的半径,点C在⊙O上,连接AC、BC , 若∠A=20°,∠B=70°,则∠ACB的度数为( )
A. 50° B. 55° C. 60° D. 65°
4.(2019九上·呼兰期中)如图,四边形 为 的内接四边形,若 ,则 的度数是( )
A. B. C. D.
5.(2020·白云模拟)如图,已知等边 的内切圆 半径为3,则 的长为 ( )
A. B. C. D.
6.(2019九上·呼和浩特期中)如图,AB为⊙O的弦,AB=8,OC⊥AB于点D,交⊙O于点C,且CD=1,则⊙O的半径为( )
A. 8.5 B. 7.5 C. 9.5 D. 8
7.(2019九上·通州期末)如图, 的半径为4,点A,B在 上,点P在 内, , ,如果 ,那么OP的长为
A. B. 3 C. D.
8.(2019九上·江都月考)如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( )
A. 22 B. 24 C. D.
9.(2021·苏州模拟)如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为 ,M 是圆上一点,∠BMO=120°.⊙C的圆心C的坐标是( )
A. B. C. D.
10.(2021·重庆模拟)如图, 是 的直径, 为 的弦,且 于点 ,点 为圆上一点,若 , , ,则 的长为( )
A. B. C. 4 D. 5
二、填空题
11.(2020九上·泰州月考)已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是________.
12.(2019·云南模拟)如果圆锥的侧面展开图的扇形半径是6,弧长是4π,那么这个扇形的圆心角为________.
13.(2020九上·河北期中)以 为中心点的量角器与直角三角板 如图所示摆放,直角顶点 在零刻度线所在直线 上,且量角器与三角板只有一个公共点 ,若点 的读数为135°,则 的度数是________.
14.(2019九上·滨湖期末)如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=65°,则∠ACD=________°.
15.(2020九上·龙凤期末)已知 的半径为 ,直线 与 相交,则圆心 到直线 距离 的取值范围是 .
16.(2020·灌南模拟)如图,在 中, , , ,经过点 且与边 相切的动圆与 , 分别相交于点 , ,则线段 长度的最小值是________.
17.(2019·平阳模拟)婷婷在发现一个门环的示意图如图所示.图中以正六边形ABCDEF的对角线AC的中点O为圆心,OB为半径作⊙O,AQ切⊙O于点P,并交DE于点Q,若AQ=12 cm,则该圆的半径为________cm.
18.(2021九上·江都期末)如图,半径为4cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设 的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为________.
三、解答题
19.(2020九上·保山月考)如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC. 求证:AD是半圆O的切线.
20.(2021·北辰模拟)如图,在 中,直径 与弦 相交于点 , .
(Ⅰ)如图①,若 ,求 和 的大小;
(Ⅱ)如图②,若 ,过点 作 的切线 ,与 的延长线相交于点 .求 的大小.
21.(2021·河东模拟)已知AB为 的直径,EF切 于点D , 过点B作 于点H交 于点C , 连接BD .
(1)如图①,若 ,求 的大小;
(2)如图②,若C为弧BD的中点,求 的大小.
四、综合题
22.(2020·黔南)如图,已知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F,交AC边于点E,点F是弧EB的中点,∠C=90°,连接AF.
(1)求证:直线CD是⊙O切线.
(2)若BD=2,OB=4,求tan∠AFC的值.
23.(2019九上·诸暨月考)如图,⊙O的直径AB=20,P是AB上(不与点A,B重合)的任一点,点C,D为⊙O上的两点,若∠APD=∠BPC,则称∠DPC为直径AB的“回旋角”,利用圆的对称性可知:“回旋角”∠DPC的度数与弧CD的度数相等.
(1)若∠DPC为直径AB的“回旋角”,且∠DPC=100°,求∠APD的大小;
(2)若直径AB的“回旋角”为90°,且△PCD的周长为 ,求AP的长.
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】解:∵点A(2,1)到x轴的距离为1,圆的半径=1,
∴点A(2,1)到x轴的距离=圆的半径,
∴圆与x轴相切;
故答案为:B.
【分析】利用点到直线的距离跟半径大小进行比较即可判断直线和圆的位置关系。
2.【答案】 C
【解析】【解答】解: ⊙O是△ABC的内切圆
∴BO、CO分别平分∠ABC、∠ACB
又 ∠ABC=50°,∠ACB=80°
∴ =25°、 °
∴ 180° =115°
故答案为:C.
【分析】根据 ⊙O是三角形△ABC的内切圆,知BO、CO是三角形的角平分线,从而求出 ∠OBC及∠OCB的度数,利用三角形内角和定理,便可找到答案.
3.【答案】 A
【解析】【解答】连接OC,∵OA=OC,∴∠OCA=∠A=20°,∵OC=OB,∴∠OCB=∠B=70°,∴∠ACB=∠OCB-∠OCA=70°-20°=50°,
故答案为:A.
【分析】连接OC,根据OA=OC,得出∠OCA=∠A=20°,再根据OC=OB,得出∠OCB=∠B=70°,即可求出∠ACB=∠OCB-∠OCA=50°.
4.【答案】 D
【解析】【解答】解:∵四边形 为 的内接四边形, ,
∴∠ABC=70°,
∴∠AOC=2∠ABC=140°,
故答案为:D.
【分析】先根据圆内接四边形的性质得到∠ABC的度数,再根据圆心角等于同弧所对圆周角的2倍即可得到答案.
5.【答案】 C
【解析】【解答】解:连接OB、OD.
∵△ABC是等边三角形,
∴∠ABC=60°,
∵⊙o为等边△ABC的内切圆,
∴∠OBD=∠ABC=30°,OD⊥AB,BD=AD,
∴OB=2OD=6,
∴BD==3 ,
∴AB=6.
故答案为:C.
【分析】连接OB、OD,根据圆内切三角形的性质可得∠OBD、∠ODB的度数及BD=AD,然后利用勾股定理计算出BD的长,即可得到AB的长.
6.【答案】 A
【解析】【解答】解:如图所示:连接 ,则 长为半径.
∵ 于点 ,
∴ ,
∵在 中, ,
∴ ,
∴ ,
故答案为A.
【分析】根据垂径定理得到直角三角形,求出 的长,连接 ,得到直角三角形,然后在直角三角形中计算出半径的长.
7.【答案】 D
【解析】【解答】解:如图,连接OB,作 交OP的延长线于M,作 交MB的延长线于 则四边形AOMN是矩形,
,
、O、P、B四点共圆,
,
,
,
,设 , ,
在 中, ,
解得 负根已经舍弃 ,
, , ,
, ,
,
,
∽ ,
,
,
,
.
故答案为:D.
【分析】如图,连接OB,作 交OP的延长线于M,作 交MB的延长线于 则四边形AOMN是矩形,推出A、O、P、B四点共圆,根据圆周角定理得到 ,根据三角函数的定义设 , ,根据勾股定理得到 负根已经舍弃 ,根据相似三角形的性质即可得到结论.
8.【答案】 B
【解析】【解答】根据题意可得直线经过定点D(3,4),则OD=5,当OD⊥BC时,BC取得最小值,根据垂径定理可得BC=24.
【分析】根据直线经过定点D(3,4),求出最短的弦BC是过点D且该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心过点A(13,0 ),求出OB的长,然后利用勾股定理求出BD即可.
9.【答案】 C
【解析】【解答】解:连接 AB,OC,
∵∠AOB=90°,
∴AB为⊙C的直径,
∵∠BMO=120°,
∴∠BAO=60°,
∴∠BCO=2∠BAO=120°,
过 C 作 CD⊥OB 于 D,则 OD= OB,∠DCB=∠DCO=60°,
∵B(﹣ ,0),,
∴BD=OD= .
在 Rt△COD 中.CD=OD tan30°= ,
∴C(﹣ , ),
故答案为:C
【分析】 连接 AB,OC,利用圆周角定理可证得AB是圆O的直径,利用圆内接四边形的性质可求出∠BAO=60°,利用圆周角定理可求出∠BCO的度数;过 C 作 CD⊥OB 于 D,利用垂径定理,由点B的坐标,可求出OD的长;再利用解直角三角形求出CD的长;即可得到点C的坐标.
10.【答案】 A
【解析】【解答】解:如图,连接 交 于 ,设 交 于 ,过点 作 于 .
,
,
,
,
,
,
, ,
,
,
,
是直径,
,
,
,
,
,
,
, ,
,
,
,
,
, ,
,
,
,
,
,
,
,
,
, ,
,
,
故答案为:A.
【分析】连接 交 于 ,设 交 于 ,过点 作 于 ,由垂径定理和等量代换易得 , 由垂径定理推论可得 , 易得 , 即可得AE=CJ,由直径所对的圆周角是直角可得∠F=∠CJT=90°,易得 , 得BT=CT,易证 , 由等量代换和勾股定理可得结果.
二、填空题
11.【答案】
【解析】【解答】解: 四边形ABCD内接于⊙O,
∴∠ABC+∠ADC=
又∵∠ABC=70°
∴∠ADC= -∠ABC= - =
故答案为: .
【分析】根据圆内接四边形的对角互补即可得到答案.
12.【答案】 120°
【解析】【解答】设这个扇形的圆心角为n°,
则 =4π,
解得,n=120,
故答案为:120°.
【分析】根据弧长公式和已知条件可得 , 解方程可求解。
13.【答案】 45
【解析】【解答】解:∵AB是⊙O的切线,
∴∠OPB=90°,
∵∠ABC=90°,
∴OP∥BC ,
∵点 的读数为135°,
∴∠EOP=135°
∴∠POB=180°-135°=45°
∴∠CBD=∠POB=45°,
故答案为:45.
【分析】根据切线的性质,求出∠OPB=90°,证明得到OP∥BC,根据平行线的性质即可得到∠POB=∠CBD,得到答案即可。
14.【答案】 40
【解析】【解答】∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,∠ACB=90°,
∴∠ADC=180°﹣∠ABC=115°,∠BAC=90°﹣∠ABC=25°,
∵过点C的切线与边AD所在直线垂直于点M,
∴∠MCA=∠ABC=65°,∠AMC=90°,
∵∠ADC=∠AMC+∠DCM,
∴∠DCM=∠ADC﹣∠AMC=25°,
∴∠ACD=∠MCA﹣∠DCM=65°﹣25°=40°,
故答案为:40.
【分析】由圆内接四边形的性质求出∠ADC=180°-∠ABC=115°,由圆周角定理求出∠ACB=90°,得出∠BAC=25°,由过点C的切线与边AD所在直线垂直于点M,可得∠MCA=∠ABC=65°,∠AMC=90°,继而根据三角形的外角性质得出∠DCM=∠ADC-∠AMC=25°,即可求出∠ACD的度数.
15.【答案】
【解析】【解答】∵⊙O的半径为5,直线AB与⊙O相交,
∴圆心到直线AB的距离小于圆的半径,
即0≤d<5;
故答案为:0≤d<5.
【分析】根据直线AB和圆相交,则圆心到直线的距离小于圆的半径即可得到问题答案。
16.【答案】
【解析】【解答】解:设圆心为F, 与 的切点为 ,
, , ,
是 的直径,
连接 ,连接 , ,
∵点 、 在 上, 是 的直径
,
又∵
∴ ,
∵ 与 切于点 ,
∴ ;
∴当点 是 的斜边 的高的中点时, 三点共线,且 为 的斜边 的高,此时 的直径等于
又∵ ,
∴ 能取到最小值4.8.
故答案为:
【分析】设圆心为F,圆F与AB的切点为D,连接FD、CF、CD,则有 ;由勾股定理的逆定理知, 是直角三角形,直径 ,由线段最短知 ,即 ,只有当点F在CD上,且CD是直角三角形ABC的斜边AB的高上CD时, 有最小值为CD的长,由直角三角形的面积公式知,此时 .
17.【答案】
【解析】【解答】解:连接OB,OP,
∵AB=BC,O为AC的中点,
∴OB⊥AC,
∵AQ是⊙O的切线,
∴OP⊥AQ,
设该圆的半径为r,
∴OB=OP=r,
∵∠ABC=120°,
∴∠BAO=30°,
∴AB=BC=CD=2r,AO= ,
∴AC= ,
∴sin∠PAO= ,
过Q作QG⊥AC于G,过D作DH⊥QG于H,
则四边形DHGC是矩形,
∴HG=CD,DH=CG,∠HDC=90°,
∴sin∠PAO= ,∠QDH=120°﹣90°=30°,
∴QG=12,
∴AG= ,
∴QH=12﹣2r,DH= ,
∴tan∠QDH=tan30°= ,
解得r= ,
∴该圆的半径为 cm,
故答案为: .
【分析】连接OB,OP,设该圆的半径为r,根据等腰三角形的三线合一得出OB⊥AC,根据切线的性质得出OP⊥AQ,设该圆的半径为r,根据正六边形的性质得出∠ABC=120°,根据三角形的内角和及等边对等角得出∠BAO=30°,根据含30°直角三角形的性质得出AB=BC=CD=2r,AO= ,故AC= ,过Q作QG⊥AC于G,过D作DH⊥QG于H,则四边形DHGC是矩形,根据矩形的性质得出HG=CD,DH=CG,∠HDC=90°,根据正弦函数的定义,由sin∠PAO= 算出QG的长,进而根据tan∠QDH= 即可求出r的长得出答案。
18.【答案】
【解析】【解答】解:如图,连OI,PI,AI,
∵△OPH的内心为I,
∴∠IOP=∠IOA,∠IPO=∠IPH,
∴∠PIO= -∠IPO-∠IOP= - (∠HOP+∠OPH),
而PH⊥OA,即∠PHO= ,
∴∠PIO= - (∠HOP+∠OPH)= - ( - )= ,
又∵OP=OA,OI公共,
而∠IOP=∠IOA,
∴△OPI≌△OAI,
∴∠AIO=∠PIO= ,
所以点I在以OA为弦,并且所对的圆周角为 的一段劣弧上;
过A、I、O三点作⊙O′,如图,连O′A,O′O,
在优弧AO上取点P,连PA,PO,
∵∠AIO= ,
∴∠APO= - = ,
∴∠A O= ,而OA=4cm,
∴∠AO = ,
∴O′O= OA= ×4=2 ,
∴弧OA的长= (cm),
所以内心I所经过的路径长为 cm.
故答案为: cm..
【分析】如图,连OI,PI,AI,由△OPH的内心为I,可得到∠PIO= -∠IPO-∠IOP= - (∠HOP+∠OPH)= ,并且易证△OPI≌△OAI,得到∠AIO=∠PIO= ,所以点I在以OA为弦,并且所对的圆周角为 的一段劣弧上;过A、I、O三点作⊙O′,如图,连O′A,O′O,在优弧AO上取点P,连PA,PO,可得∠APO= - = ,得∠A O= , OA= ×4=2 ,然后利用弧长公式计算弧OA的长.
三、解答题
19.【答案】 解:∵AB为半圆O的直径,
∴∠BCA=90°,
又∵BC∥OD,
∴∠OEA=90°,即OD⊥AC,
∴∠D+∠DAE=90°,
∵∠D=∠BAC,
∴∠BAC+∠DAE=90°,即∠DAB=90°,
∴OA⊥AD,
∴AD是半圆O的切线.
【解析】【分析】根据圆的性质及平行线的性质证得OD⊥AC,从而得到∠D+∠DAE=90°,再进行等量代换即可证明结论.
20.【答案】 解:(Ⅰ)∵ ,
∴∠C=
∴
∵直径 与弦 相交于点 ,
∴∠ADB=90°,
又∵
∴
(Ⅱ)∵
∴∠AEC=90°
又∵
∴
∴
∵ 是 的切线
∴
∴
【解析】【分析】(Ⅰ)先求出 ,再求出 ∠ADB=90°, 最后计算求解即可;
(Ⅱ)先求出 ∠AEC=90° ,再求出 ,最后计算求解即可。
21.【答案】 (1)如图,连接OD.
由切线的性质结合题意可知 ,
∴ ,
∴ .
∵ ,
∴ .
∵ ,
∴ ,
∴ .
∴ .
(2)如图,连接OD、OC、CD.
∵OC=OD,
∴ .
∵ ,即 ,
∴ ,
∵ ,
∴ .
∵C为 中点,
∴ ,
由(1)可知 ,
∴ ,
∵ ,
∴ .
∴ .
【解析】【分析】(1)先求出 ,再求出 ,最后计算求解即可;
(2)先求出 , 再求出 ,最后计算求解即可。
四、综合题
22.【答案】 (1)证明:连结OF,BE,如图:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵∠C=90°,
∴∠AEB=∠ACD,
∴BE∥CD,
∵点F是弧BE的中点,
∴OF⊥BE,
∴OF⊥CD,
∵OF为半径,
∴直线DF是⊙O的切线;
(2)解:∵∠C=∠OFD=90°,
∴AC∥OF,
∴△OFD∽△ACD,
∴ = ,
∵BD=2,OF=OB=4,
∴OD=6,AD=10,
∴AC= = = ,
∴CD= = = ,
∵AC∥OF,OA=4,
∴ = ,即 = ,
解得:CF= ,
∴tan∠AFC= = = .
【解析】【分析】(1)连结OF,BE,得到BE∥CD,根据根据垂径定理及平行线的性质得到CD⊥OF,即可得出结论;
(2)首先判断出 △OFD∽△ACD ,由相似三角形的性质求出AC长,再由勾股定理可求得DC长,进而根据平行线分线段成比例能求出CF长,最后根据正切函数的定义即可得出结果.
23.【答案】 (1)解:∵ ∠DPC为直径AB的“回旋角”,且∠DPC=100°, 由题意得: ∠APD=∠BPC =(180°-100)÷2=40°.
(2)解:延长DP交圆于F点,连接CF,过O作OH⊥FD,∵ ∠APD=∠BPC=(180°-90°)÷2=45°,∵∠APD=∠BPF, ∴ ∠FPB=∠BPC,则由圆的对称性知,PC=PF,∴FD=PC+PD,由题中定义可知, ∠DPC = ∠DOC=90°,∴DC=OC=10 , ∴FD=PD+PC=16+10-10=16,∵DH=FD=8,∵OH= , ∴PO==6 , ∴AP=OA-OP=10-6.当A、B对调时,即P在OB之间时,AP=OA+OP=10+6.
