人教版数学七年级下册6.1算数平方根课件(共27张PPT)
文档属性
| 名称 | 人教版数学七年级下册6.1算数平方根课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 20:07:03 | ||
图片预览






文档简介
(共27张PPT)
算数平方根
人教版数学 七年级下册
学习目标
01
学习目标
理解算术平方根的概念,会用根号表示正数的算术平方根。
理解算术平方根的非负性。
通过平方运算求某些非负数的算术平方根。
新课教学
02
有理数乘方知识点回顾
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
an
幂
底数
指数
(运算结果)
(相同的因数)
概念:
练一练
(相同因数的个数)
1
4
25
知识回顾
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
因为25,所以正方形的边长为5 dm
新课引入
25 dm2
?
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
因为25,所以正方形的边长为5 dm
新课引入
25 dm2
5dm
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
若题中的面积变为下表中的数值,你能知道它的正方形边长吗?
1
3
4
6
小游戏:对于正方形的面积,你可以举出其它数据并求出它的边长吗?
观察这几组数据,你发现了什么?
运算过程实质是:在有理数乘方中,已知指数和幂,求底数的过程。
新课引入
a
(a > 0)
算术平方根
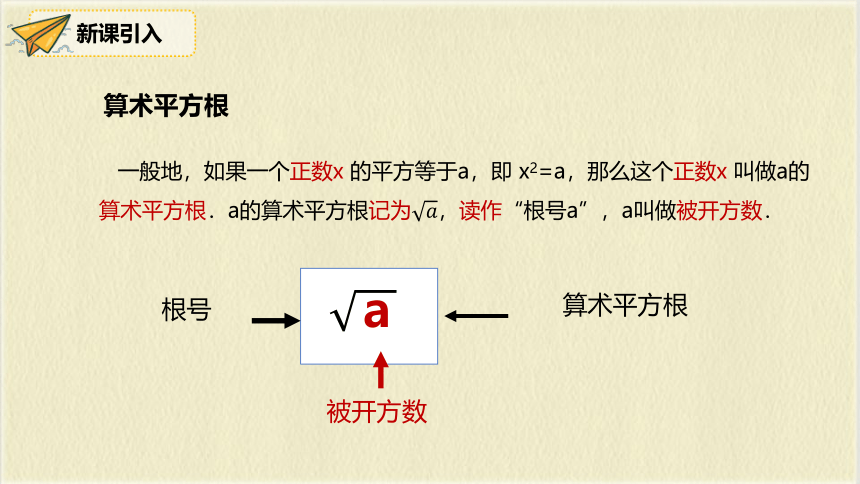
一般地,如果一个正数x 的平方等于a,即 x2=a,那么这个正数x 叫做a的算术平方根.a的算术平方根记为,读作“根号a”,a叫做被开方数.
根号
被开方数
算术平方根
a
新课引入
算术平方根性质
1)正数只有一个算术平方根,且恒为正;
2)0的算术平方根为0(规定);
3)负数没有算术平方根。
由算数平方根的性质可知的意义是什么?
新课引入
课堂检测
03
1.判断下列说法是否正确:
正确
错误
错误
错误
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
小试牛刀
2.求下列各数的算术平方根:
1)100
2)0.0001
3)81
4)7
5)
解:(1)因为102=100,
所以100的算术平方根是10.
即.
(2)因为0.012=0.0001,
所以0.0001的算术平方根是0.01.
即.01.
小试牛刀
解:(3)因为92=81,
所以81的算术平方根是9.
即.
(4)因为72=49,
所以72的算术平方根是7.
即.
2.求下列各数的算术平方根:
1)100
2)0.0001
3)81
4)7
5)
小试牛刀
解:(5)因为,
所以的算术平方根是.
即.
2.求下列各数的算术平方根:
1)100
2)0.0001
3)81
4)7
5)
小试牛刀
2.观察下列各数的算术平方根,你发现它们的大小关系存在什么联系吗?
1)
2)
3)
4)
5)
被开方数越大,对应的算术平方根也越大。
小试牛刀
2.求下列各数的算术平方根:
(1)81; (2) ; (3)
小试牛刀
3.下列各式是否有意义
小试牛刀
(1); (2)
(3)
4.若,则 =______。
【详解】
解:∵,
∴,
∴,
故答案为:.
小试牛刀
5.已知a是最小正整数,b是的算术平方根,则a+b的值是_____。
【详解】
∵a是最小正整数,
∴a=1,
∵=9,b是的算术平方根,
∴b==3,
∴a+b=1+3=4.
故答案为:4
小试牛刀
6.若,则_____。
【详解】
解:∵,
∴x+1=4,即x=3.
故答案为:3
小试牛刀
7.自由下落物体下落的距离h(米)与下落时间t(秒)的关系为 .有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
小试牛刀
解:将h=19.6代入关系式 ,得
因为t是非负数,所以 (S)
所以到达地面需要2S。
延伸拓展
04
计算若,那么a2019 b2020=____________。
【详解】
∵,
∴(a+1)2=0,b-1=0,
解得:a=-1,b=1,
∴a2019+b2020=-1+1=0,
故答案为:0
延伸拓展
课堂小结
05
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定: 0 的算术平方根是 0.
依据算术平方根的定义,可求得某一个非负数的算术平方根.
由算术平方根的定义,
得
a≥0
课堂小结
谢谢观看!
注:本视频所有素材来源于网络,如有侵权,请联系我们。
算数平方根
人教版数学 七年级下册
学习目标
01
学习目标
理解算术平方根的概念,会用根号表示正数的算术平方根。
理解算术平方根的非负性。
通过平方运算求某些非负数的算术平方根。
新课教学
02
有理数乘方知识点回顾
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
an
幂
底数
指数
(运算结果)
(相同的因数)
概念:
练一练
(相同因数的个数)
1
4
25
知识回顾
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
因为25,所以正方形的边长为5 dm
新课引入
25 dm2
?
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
因为25,所以正方形的边长为5 dm
新课引入
25 dm2
5dm
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
若题中的面积变为下表中的数值,你能知道它的正方形边长吗?
1
3
4
6
小游戏:对于正方形的面积,你可以举出其它数据并求出它的边长吗?
观察这几组数据,你发现了什么?
运算过程实质是:在有理数乘方中,已知指数和幂,求底数的过程。
新课引入
a
(a > 0)
算术平方根
一般地,如果一个正数x 的平方等于a,即 x2=a,那么这个正数x 叫做a的算术平方根.a的算术平方根记为,读作“根号a”,a叫做被开方数.
根号
被开方数
算术平方根
a
新课引入
算术平方根性质
1)正数只有一个算术平方根,且恒为正;
2)0的算术平方根为0(规定);
3)负数没有算术平方根。
由算数平方根的性质可知的意义是什么?
新课引入
课堂检测
03
1.判断下列说法是否正确:
正确
错误
错误
错误
(1) 5 是 25 的算术平方根;
(4) 2 是 -4 的算术平方根.
(3) 0.01 是 0.1 的算术平方根;
(2) -7 是 49 的算术平方根;
小试牛刀
2.求下列各数的算术平方根:
1)100
2)0.0001
3)81
4)7
5)
解:(1)因为102=100,
所以100的算术平方根是10.
即.
(2)因为0.012=0.0001,
所以0.0001的算术平方根是0.01.
即.01.
小试牛刀
解:(3)因为92=81,
所以81的算术平方根是9.
即.
(4)因为72=49,
所以72的算术平方根是7.
即.
2.求下列各数的算术平方根:
1)100
2)0.0001
3)81
4)7
5)
小试牛刀
解:(5)因为,
所以的算术平方根是.
即.
2.求下列各数的算术平方根:
1)100
2)0.0001
3)81
4)7
5)
小试牛刀
2.观察下列各数的算术平方根,你发现它们的大小关系存在什么联系吗?
1)
2)
3)
4)
5)
被开方数越大,对应的算术平方根也越大。
小试牛刀
2.求下列各数的算术平方根:
(1)81; (2) ; (3)
小试牛刀
3.下列各式是否有意义
小试牛刀
(1); (2)
(3)
4.若,则 =______。
【详解】
解:∵,
∴,
∴,
故答案为:.
小试牛刀
5.已知a是最小正整数,b是的算术平方根,则a+b的值是_____。
【详解】
∵a是最小正整数,
∴a=1,
∵=9,b是的算术平方根,
∴b==3,
∴a+b=1+3=4.
故答案为:4
小试牛刀
6.若,则_____。
【详解】
解:∵,
∴x+1=4,即x=3.
故答案为:3
小试牛刀
7.自由下落物体下落的距离h(米)与下落时间t(秒)的关系为 .有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
小试牛刀
解:将h=19.6代入关系式 ,得
因为t是非负数,所以 (S)
所以到达地面需要2S。
延伸拓展
04
计算若,那么a2019 b2020=____________。
【详解】
∵,
∴(a+1)2=0,b-1=0,
解得:a=-1,b=1,
∴a2019+b2020=-1+1=0,
故答案为:0
延伸拓展
课堂小结
05
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定: 0 的算术平方根是 0.
依据算术平方根的定义,可求得某一个非负数的算术平方根.
由算术平方根的定义,
得
a≥0
课堂小结
谢谢观看!
注:本视频所有素材来源于网络,如有侵权,请联系我们。
