人教版数学九年级上册24.2.1点和圆的位置关系课件 (共18张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.2.1点和圆的位置关系课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 524.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 20:53:02 | ||
图片预览



文档简介
(共18张PPT)
24.2.1点与圆的位置关系
如图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
问题引入
解决这个问题要研究点和圆的位置关系.
.
o
.
.
.C
.
.
.
. B
.
.A
.
.
.
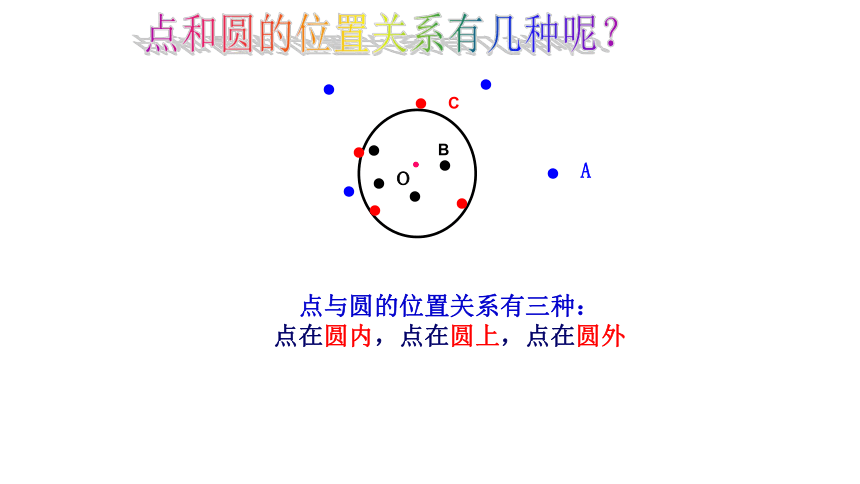
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外
点和圆的位置关系有几种呢?
r
问题二:
设⊙O半径为r,说出点A,点B,点C与圆心O的距离与半径的关系:
·
C
O
A
B
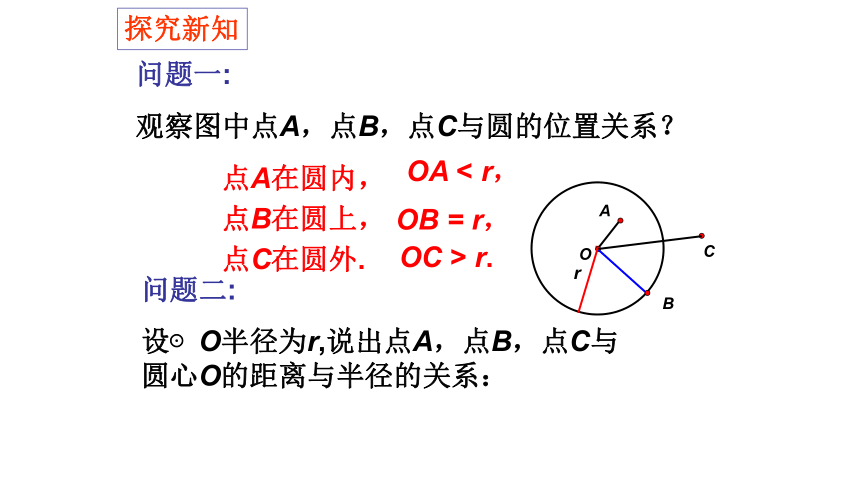
OC > r.
问题一:
观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r,
OB = r,
探究新知
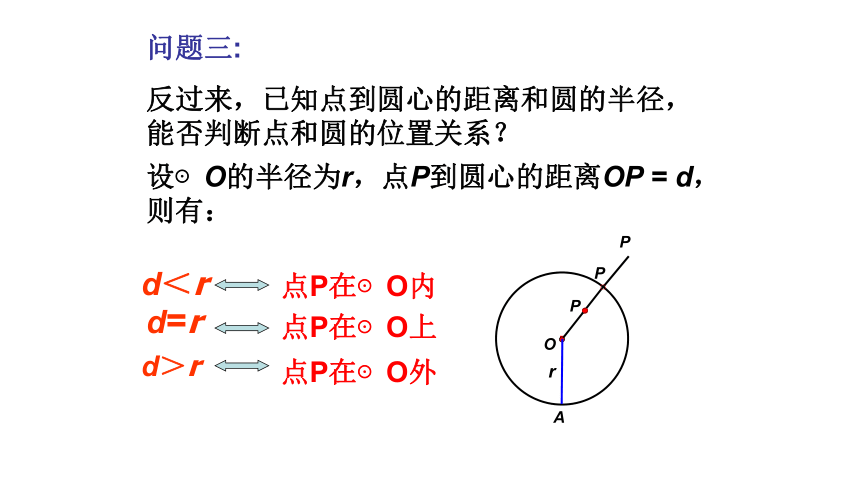
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
r
·
O
A
问题三:
反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
P
P
P
点A在⊙O内
d<r
d=r
d>r
点B在⊙O上
点P在⊙O内
点P在⊙O上
点P在⊙O外
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域,这些区域用由高到底的环数来表示,射击成绩用弹着点位置对应的环数来表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
你知道击中靶上不同位置的成绩是如何计算的吗 ?
观察与思考
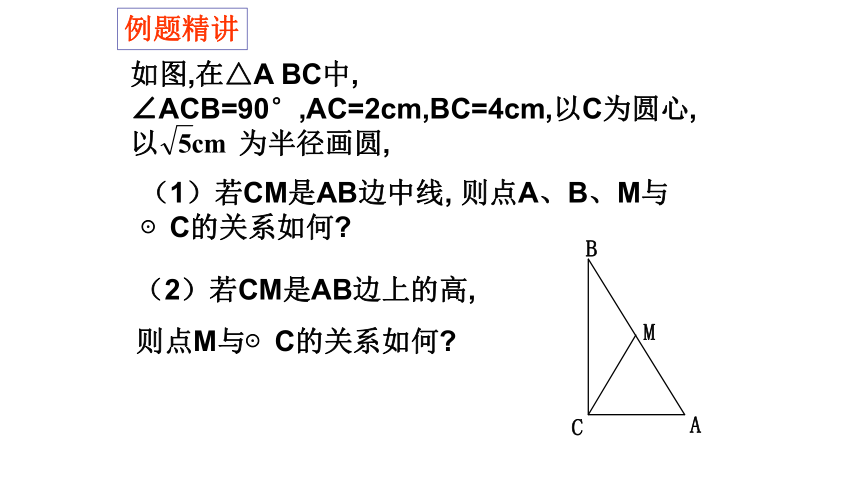
例题精讲
如图,在△A BC中, ∠ACB=90°,AC=2cm,BC=4cm,以C为圆心,以 为半径画圆,
(1)若CM是AB边中线, 则点A、B、M与 ⊙C的关系如何
(2)若CM是AB边上的高,
则点M与⊙C的关系如何
学以致用
1.⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。
圆内
圆上
圆外
2.已知圆的半径为6,点P不在圆内,则线段OP 的长度的取值范围是_________
OP≥6
3.正方形ABCD的边长为 cm,以A为圆心2cm
为半径作⊙A,则点C( )
A.在⊙A上 B.在⊙A内 C.在⊙A外 D.无法判断
C
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
探究新知
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
●O
● O
●O
●O
A
B
无数个。它们的圆心都在线段AB的垂直平分线上。
探究新知
3.平面上有三点A、B、C不在同一直线上经过A、B、C三点的圆有几个?圆心在哪里?
结论:
不在同一条直线上的三个点确定一个圆。
┓
●B
●C
┏
●A
●O
探究新知
经过三角形三个顶点可以画一个圆,并且只能画一个.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
想一想
●O
A
B
C
有关概念
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
做一做:
辨一辨
1、过三点一定可以作圆 ( )
5、三角形的外心到三边的距离相等 ( )
2、三角形有且只有一个外接圆 ( )
3、任意一个圆有一个内接三角形,
并且只有一个内接三角形 ( )
4、三角形的外心就是这个三角形任意两边
垂直平分线的交点 ( )
·
1、⊙O的半径6,当OP=6时,点P在 ;当OP 时点P在圆内;当OP 时,点P不在圆外。
圆上
<6
≤6
随堂练习
2、画出由所有到已知点O的距离大于或等于2CM并且小于或等于3CM的点组成的图形。
O
3cm
2cm
3、已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO__________。
随堂练习
圆外
圆内
5
≤5
小结:
1.点与圆的位置关系
2.不在同一条直线上的三个点确定一个圆。
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
点A在⊙O内
d<r
d=r
d>r
点P在⊙O内
点P在⊙O上
点P在⊙O外
3.三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
谢谢观看!
24.2.1点与圆的位置关系
如图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
问题引入
解决这个问题要研究点和圆的位置关系.
.
o
.
.
.C
.
.
.
. B
.
.A
.
.
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外
点和圆的位置关系有几种呢?
r
问题二:
设⊙O半径为r,说出点A,点B,点C与圆心O的距离与半径的关系:
·
C
O
A
B
OC > r.
问题一:
观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r,
OB = r,
探究新知
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
r
·
O
A
问题三:
反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
P
P
P
点A在⊙O内
d<r
d=r
d>r
点B在⊙O上
点P在⊙O内
点P在⊙O上
点P在⊙O外
射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域,这些区域用由高到底的环数来表示,射击成绩用弹着点位置对应的环数来表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好.
你知道击中靶上不同位置的成绩是如何计算的吗 ?
观察与思考
例题精讲
如图,在△A BC中, ∠ACB=90°,AC=2cm,BC=4cm,以C为圆心,以 为半径画圆,
(1)若CM是AB边中线, 则点A、B、M与 ⊙C的关系如何
(2)若CM是AB边上的高,
则点M与⊙C的关系如何
学以致用
1.⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 。
圆内
圆上
圆外
2.已知圆的半径为6,点P不在圆内,则线段OP 的长度的取值范围是_________
OP≥6
3.正方形ABCD的边长为 cm,以A为圆心2cm
为半径作⊙A,则点C( )
A.在⊙A上 B.在⊙A内 C.在⊙A外 D.无法判断
C
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
探究新知
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
●O
● O
●O
●O
A
B
无数个。它们的圆心都在线段AB的垂直平分线上。
探究新知
3.平面上有三点A、B、C不在同一直线上经过A、B、C三点的圆有几个?圆心在哪里?
结论:
不在同一条直线上的三个点确定一个圆。
┓
●B
●C
┏
●A
●O
探究新知
经过三角形三个顶点可以画一个圆,并且只能画一个.
一个三角形的外接圆有几个?
一个圆的内接三角形有几个?
经过三角形三个顶点的圆叫做三角形的外接圆。
三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
这个三角形叫做这个圆的内接三角形。
三角形外接圆的圆心叫做这个三角形的外心。
想一想
●O
A
B
C
有关概念
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
做一做:
辨一辨
1、过三点一定可以作圆 ( )
5、三角形的外心到三边的距离相等 ( )
2、三角形有且只有一个外接圆 ( )
3、任意一个圆有一个内接三角形,
并且只有一个内接三角形 ( )
4、三角形的外心就是这个三角形任意两边
垂直平分线的交点 ( )
·
1、⊙O的半径6,当OP=6时,点P在 ;当OP 时点P在圆内;当OP 时,点P不在圆外。
圆上
<6
≤6
随堂练习
2、画出由所有到已知点O的距离大于或等于2CM并且小于或等于3CM的点组成的图形。
O
3cm
2cm
3、已知⊙O的面积为25π:
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上;
(4)若点P不在圆外,则PO__________。
随堂练习
圆外
圆内
5
≤5
小结:
1.点与圆的位置关系
2.不在同一条直线上的三个点确定一个圆。
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
点A在⊙O内
d<r
d=r
d>r
点P在⊙O内
点P在⊙O上
点P在⊙O外
3.三角形的外心就是三角形三条边的垂直平分线的交点,它到三角形三个顶点的距离相等。
谢谢观看!
同课章节目录
