4.3.2 一次函数的图象 课件(共33张PPT)
文档属性
| 名称 | 4.3.2 一次函数的图象 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 19:17:16 | ||
图片预览









文档简介
(共33张PPT)
新课导入
复习引入
(1)什么叫一次函数?从解析式上看,一次函数与正比例函数有什么关系?
(2)正比例函数的图象是什么?是怎样得到的?
(3)正比例函数有哪些性质?是怎样得到这些性
质的?
新课导入
正比例函数
解析式 y =kx(k≠0)
性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.
一次函数
解析式 y =kx+b(k≠0)
针对函数 y =kx+b,大家想研究什么?应该怎样研究?
图象:经过原点和
(1,k)的一条直线
x
y
O
k>0
k<0
x
y
O
?
?
4.3 一次函数的图象
第四章 一次函数
第2课时 一次函数的图象和性质
1.通过具体操作,感受一次函数的图象是一条直线.
2.学会选择正确的点,画出一次函数的图象.
3.在现实情境中会列一次函数关系式,并画出其图象解决实际问题.
讲授新课
一次函数的图象的画法
在上一课的学习中,我们学会了正比例函数图象的画法,分为三个步骤.
①列表
②描点
③连线
那么你能用同样的方法画出一次函数的图象吗?
讲授新课
画出一次函数y=-2x+1的图象.
解:列表:
x … -2 -1 0 1 2 …
y … 5 3 1 -1 -3 …
例题
讲授新课
描点
连线
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
y=-2x+1
讲授新课
总结归纳
一次函数y=kx+b的图象也称为直线y=kx+b.
一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0)
(0, b)
( , 0)
讲授新课
O
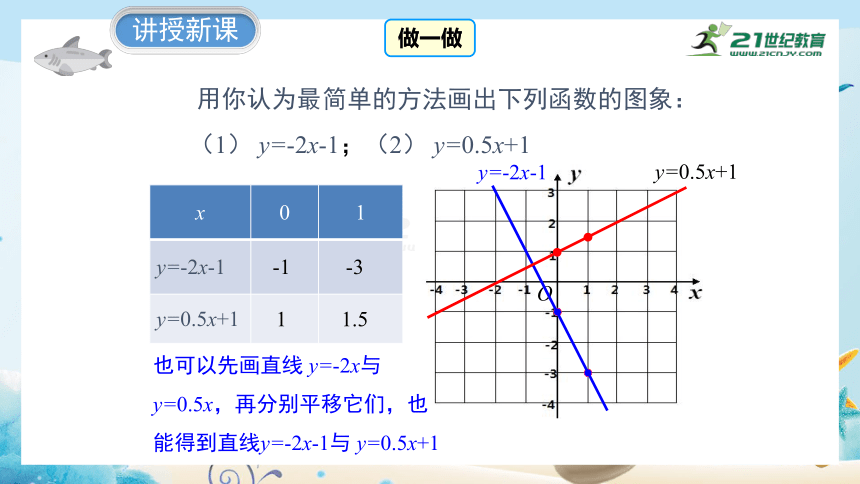
用你认为最简单的方法画出下列函数的图象:
(1) y=-2x-1;(2) y=0.5x+1
x 0 1
y=-2x-1
y=0.5x+1
-1
-3
1
y=-2x-1
做一做
1.5
y=0.5x+1
也可以先画直线 y=-2x与 y=0.5x,再分别平移它们,也能得到直线y=-2x-1与 y=0.5x+1
讲授新课
.
.
.
.
x
y
2
O
.
.
.
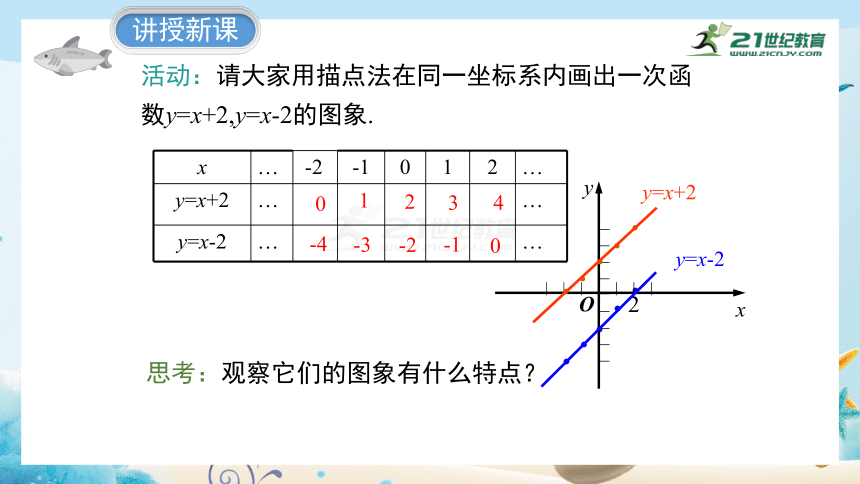
活动:请大家用描点法在同一坐标系内画出一次函数y=x+2,y=x-2的图象.
x … -2 -1 0 1 2 …
y=x+2 … …
y=x-2 … …
0
-3
1
-4
2
-2
3
-1
4
0
.
.
.
y=x+2
y=x-2
思考:观察它们的图象有什么特点?
讲授新课
y=x
y=x+2
y=x-2
y
2
O
x
2
●
●
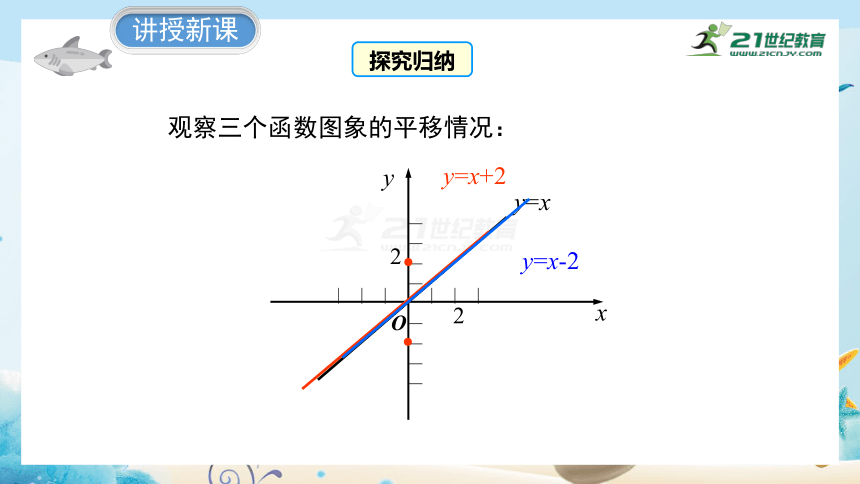
观察三个函数图象的平移情况:
探究归纳
讲授新课
把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1. 这三个函数的图象形状都是 ,并且倾斜程度
______.
2. 函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移
个单位长度而得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向____ 平移____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
比较三个函数的解析式, 相同,
它们的图象的位置关系是 .
自变量系数k
平行
讲授新课
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
思考:与x轴的交点坐标是什么?
要点归纳
用一句话来表述就是:“上加下减”;上、下是“形”的平移,加、减是“数”的变化.
讲授新课
画出一次函数y=-2x+1的图象.
解:列表:
x … -2 -1 0 1 2 …
y … 5 3 1 -1 -3 …
例题
讲授新课
描点
连线
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
y=-2x+1
讲授新课
总结归纳
一次函数y=kx+b的图象也称为直线y=kx+b.
一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0)
(0, b)
( , 0)
讲授新课
O
用你认为最简单的方法画出下列函数的图象:
(1) y=-2x-1;(2) y=0.5x+1
x 0 1
y=-2x-1
y=0.5x+1
-1
-3
1
y=-2x-1
做一做
1.5
y=0.5x+1
也可以先画直线 y=-2x与 y=0.5x,再分别平移它们,也能得到直线y=-2x-1与 y=0.5x+1
讲授新课
y=x
y=x+2
y=x-2
y
2
O
x
2
●
●
观察三个函数图象的平移情况:
探究归纳
讲授新课
把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1. 这三个函数的图象形状都是 ,并且倾斜程度
______.
2. 函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移
个单位长度而得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向____ 平移____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
比较三个函数的解析式, 相同,
它们的图象的位置关系是 .
自变量系数k
平行
讲授新课
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
思考:与x轴的交点坐标是什么?
要点归纳
用一句话来表述就是:“上加下减”;上、下是“形”的平移,加、减是“数”的变化.
讲授新课
分别在同一直角坐标系内画出下列直线,并指出每一
小题中两条直线的位置关系.
(1)y=-x+2,y=-x-1;(2)y=3x-2,y= x-2.
解:如图①和②所示.
(1)直线y=-x+2与直线y=-x-1平行,把直线y=-x+2向
下平移3个单位,即可得到直线y=-x-1;
(2)直线y=3x-2与直线y= x-2交于y轴上一点(0,-2).
①
②
例题
讲授新课
一次函数的性质
画一画1:在同一坐标系中作出下列函数的图象.
(1)
(2)
(3)
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考:k,b的值跟图象有什么关系?
讲授新课
画一画2: 在同一坐标系中作出下列函数的图象.
(1)
(2)
(3)
-3
o
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考:k,b的值跟图象有什么关系?
讲授新课
在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
由此得到一次函数性质:
归纳总结
课堂练习
1. 在同一直角坐标系中,描绘出了下列函数:
①y=-x+1;②y=x+1;③y=-x-1;④y=-2(x+1)的图象,
则下列说法正确的是( )
A.过点(-1,0)的是①③ B.交点在y轴上的是②④
C.互相平行的是①③ D.关于x轴对称的是①②
C
课堂练习
2.已知点(-4,y1),(2,y2)都在直线y=-x+2上,则y1,y2的大小关系是( )
A.y1>y2 B.y1=y2
C.y1A
课堂练习
3.已知一次函数y=(4m+1)x-(m+1).
(1)m为何值时,y随x的增大而减小
(2)m为何值时,直线与y轴的交点在x轴下方
解:(1)∵y随x的增大而减小,∴4m+1<0,解得m<-0.25 .
∴当m<-0.25时,y随x的增大而减小.
课堂练习
(2)y=(4m+1)x-(m+1)与y轴的交点坐标为(0,-m-1),
∵直线与y轴的交点在x轴下方,∴-(m+1)<0,解得m>-1.
又∵4m+1≠0,∴m≠-0.25,
∴当m>-1且m≠-0.25时,直线与y轴的交点在x轴下方.
3.已知一次函数y=(4m+1)x-(m+1).
(1)m为何值时,y随x的增大而减小
(2)m为何值时,直线与y轴的交点在x轴下方
拓展提高
4.如图所示,点P(x,y)是第一象限内一个动点,且在直线y=-2x+8上,直线与x轴交于点A.
(1)当点P的横坐标为3时,ΔAPO的面积为多少
(2)设ΔAPO的面积为S,用含x的式子表示S,并写出x的取值范围.
解:(1)令y=0,则-2x+8=0,解得x=4,所以OA=4,
因为点P(x,y)是第一象限内一个动点,且在直线y=-2x+8上,所以当x=3时,y=(-2)×3+8=2,
所以SΔAPO= ×4×2=4.
拓展提高
(2)因为点P (x,-2x+8),
所以SΔAPO=OA×(-2x+8)
= ×4×(-2x+8)
=-4x+16(04.如图所示,点P(x,y)是第一象限内一个动点,且在直线y=-2x+8上,直线与x轴交于点A.
(1)当点P的横坐标为3时,ΔAPO的面积为多少
(2)设ΔAPO的面积为S,用含x的式子表示S,并写出x的取值范围.
1.一次函数的一般形式及一次函数与正比例函数的关系.
2.一次函数的图象与性质.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
新课导入
复习引入
(1)什么叫一次函数?从解析式上看,一次函数与正比例函数有什么关系?
(2)正比例函数的图象是什么?是怎样得到的?
(3)正比例函数有哪些性质?是怎样得到这些性
质的?
新课导入
正比例函数
解析式 y =kx(k≠0)
性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.
一次函数
解析式 y =kx+b(k≠0)
针对函数 y =kx+b,大家想研究什么?应该怎样研究?
图象:经过原点和
(1,k)的一条直线
x
y
O
k>0
k<0
x
y
O
?
?
4.3 一次函数的图象
第四章 一次函数
第2课时 一次函数的图象和性质
1.通过具体操作,感受一次函数的图象是一条直线.
2.学会选择正确的点,画出一次函数的图象.
3.在现实情境中会列一次函数关系式,并画出其图象解决实际问题.
讲授新课
一次函数的图象的画法
在上一课的学习中,我们学会了正比例函数图象的画法,分为三个步骤.
①列表
②描点
③连线
那么你能用同样的方法画出一次函数的图象吗?
讲授新课
画出一次函数y=-2x+1的图象.
解:列表:
x … -2 -1 0 1 2 …
y … 5 3 1 -1 -3 …
例题
讲授新课
描点
连线
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
y=-2x+1
讲授新课
总结归纳
一次函数y=kx+b的图象也称为直线y=kx+b.
一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0)
(0, b)
( , 0)
讲授新课
O
用你认为最简单的方法画出下列函数的图象:
(1) y=-2x-1;(2) y=0.5x+1
x 0 1
y=-2x-1
y=0.5x+1
-1
-3
1
y=-2x-1
做一做
1.5
y=0.5x+1
也可以先画直线 y=-2x与 y=0.5x,再分别平移它们,也能得到直线y=-2x-1与 y=0.5x+1
讲授新课
.
.
.
.
x
y
2
O
.
.
.
活动:请大家用描点法在同一坐标系内画出一次函数y=x+2,y=x-2的图象.
x … -2 -1 0 1 2 …
y=x+2 … …
y=x-2 … …
0
-3
1
-4
2
-2
3
-1
4
0
.
.
.
y=x+2
y=x-2
思考:观察它们的图象有什么特点?
讲授新课
y=x
y=x+2
y=x-2
y
2
O
x
2
●
●
观察三个函数图象的平移情况:
探究归纳
讲授新课
把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1. 这三个函数的图象形状都是 ,并且倾斜程度
______.
2. 函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移
个单位长度而得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向____ 平移____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
比较三个函数的解析式, 相同,
它们的图象的位置关系是 .
自变量系数k
平行
讲授新课
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
思考:与x轴的交点坐标是什么?
要点归纳
用一句话来表述就是:“上加下减”;上、下是“形”的平移,加、减是“数”的变化.
讲授新课
画出一次函数y=-2x+1的图象.
解:列表:
x … -2 -1 0 1 2 …
y … 5 3 1 -1 -3 …
例题
讲授新课
描点
连线
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
y=-2x+1
讲授新课
总结归纳
一次函数y=kx+b的图象也称为直线y=kx+b.
一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过(0,b)和(1,k+b)或( ,0)
(0, b)
( , 0)
讲授新课
O
用你认为最简单的方法画出下列函数的图象:
(1) y=-2x-1;(2) y=0.5x+1
x 0 1
y=-2x-1
y=0.5x+1
-1
-3
1
y=-2x-1
做一做
1.5
y=0.5x+1
也可以先画直线 y=-2x与 y=0.5x,再分别平移它们,也能得到直线y=-2x-1与 y=0.5x+1
讲授新课
y=x
y=x+2
y=x-2
y
2
O
x
2
●
●
观察三个函数图象的平移情况:
探究归纳
讲授新课
把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1. 这三个函数的图象形状都是 ,并且倾斜程度
______.
2. 函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移
个单位长度而得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向____ 平移____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
比较三个函数的解析式, 相同,
它们的图象的位置关系是 .
自变量系数k
平行
讲授新课
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
思考:与x轴的交点坐标是什么?
要点归纳
用一句话来表述就是:“上加下减”;上、下是“形”的平移,加、减是“数”的变化.
讲授新课
分别在同一直角坐标系内画出下列直线,并指出每一
小题中两条直线的位置关系.
(1)y=-x+2,y=-x-1;(2)y=3x-2,y= x-2.
解:如图①和②所示.
(1)直线y=-x+2与直线y=-x-1平行,把直线y=-x+2向
下平移3个单位,即可得到直线y=-x-1;
(2)直线y=3x-2与直线y= x-2交于y轴上一点(0,-2).
①
②
例题
讲授新课
一次函数的性质
画一画1:在同一坐标系中作出下列函数的图象.
(1)
(2)
(3)
-3
O
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考:k,b的值跟图象有什么关系?
讲授新课
画一画2: 在同一坐标系中作出下列函数的图象.
(1)
(2)
(3)
-3
o
-2
2
3
1
2
3
-1
-1
-2
x
y
1
思考:k,b的值跟图象有什么关系?
讲授新课
在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
由此得到一次函数性质:
归纳总结
课堂练习
1. 在同一直角坐标系中,描绘出了下列函数:
①y=-x+1;②y=x+1;③y=-x-1;④y=-2(x+1)的图象,
则下列说法正确的是( )
A.过点(-1,0)的是①③ B.交点在y轴上的是②④
C.互相平行的是①③ D.关于x轴对称的是①②
C
课堂练习
2.已知点(-4,y1),(2,y2)都在直线y=-x+2上,则y1,y2的大小关系是( )
A.y1>y2 B.y1=y2
C.y1
课堂练习
3.已知一次函数y=(4m+1)x-(m+1).
(1)m为何值时,y随x的增大而减小
(2)m为何值时,直线与y轴的交点在x轴下方
解:(1)∵y随x的增大而减小,∴4m+1<0,解得m<-0.25 .
∴当m<-0.25时,y随x的增大而减小.
课堂练习
(2)y=(4m+1)x-(m+1)与y轴的交点坐标为(0,-m-1),
∵直线与y轴的交点在x轴下方,∴-(m+1)<0,解得m>-1.
又∵4m+1≠0,∴m≠-0.25,
∴当m>-1且m≠-0.25时,直线与y轴的交点在x轴下方.
3.已知一次函数y=(4m+1)x-(m+1).
(1)m为何值时,y随x的增大而减小
(2)m为何值时,直线与y轴的交点在x轴下方
拓展提高
4.如图所示,点P(x,y)是第一象限内一个动点,且在直线y=-2x+8上,直线与x轴交于点A.
(1)当点P的横坐标为3时,ΔAPO的面积为多少
(2)设ΔAPO的面积为S,用含x的式子表示S,并写出x的取值范围.
解:(1)令y=0,则-2x+8=0,解得x=4,所以OA=4,
因为点P(x,y)是第一象限内一个动点,且在直线y=-2x+8上,所以当x=3时,y=(-2)×3+8=2,
所以SΔAPO= ×4×2=4.
拓展提高
(2)因为点P (x,-2x+8),
所以SΔAPO=OA×(-2x+8)
= ×4×(-2x+8)
=-4x+16(0
(1)当点P的横坐标为3时,ΔAPO的面积为多少
(2)设ΔAPO的面积为S,用含x的式子表示S,并写出x的取值范围.
1.一次函数的一般形式及一次函数与正比例函数的关系.
2.一次函数的图象与性质.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
