4.4.2 一次函数的应用 课件(共29张PPT)
文档属性
| 名称 | 4.4.2 一次函数的应用 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 19:28:11 | ||
图片预览






文档简介
(共29张PPT)
在一次函数y=kx+b中
当k>0 时,y 随x的增大而增大,
当b>0 时,直线交y轴于正半轴,
必过一、二、三象限;
当b<0 时,直线交y轴于负半轴,
必过一、三、四象限;
回顾与复习
在一次函数y=kx+b中
当k<0 时,y随x的增大而减小,
当b>0 时,直线交y轴于正半轴,
必过一、二、四象限;
当b<0 时,直线交y轴于负半轴,
必过二、三、四象限.
回顾与复习
4.4 一次函数的应用
第四章 一次函数
第2课时 借助单个一次函数图象解决简单实际问题
单个一次函数图象的应用
1.利用一次函数图象解决实际问题,关键是找到图象中两个变量之间的数量关系,把实际问题抽象、升华为一次函数模型,即建模,再利用一次函数的相关性质解决实际问题,常见类型如下:
(1) 题目中已知一次函数的关系式,可直接运用一
次函数的性质求解;
讲授新课
(2)题目中没有给出一次函数的关系式,而是通过语言、表格或图象给出一次函数的情境,这时需要先根据题目中给出的信息求出一次函数的关系式,再利用一次函数的性质解决实际问题.
2.要点精析:“建模”可以把实际问题转化为关于一次
函数的数学问题,它的关键是确定函数与自变量之间
的关系式,并确定实际问题中自变量的取值范围.
讲授新课
讲授新课
例题
由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.蓄水量V(万m3)与干旱持续时间 t( 天) 的关系如图所示,
讲授新课
0 10 20 30 40 50 t/天
V/
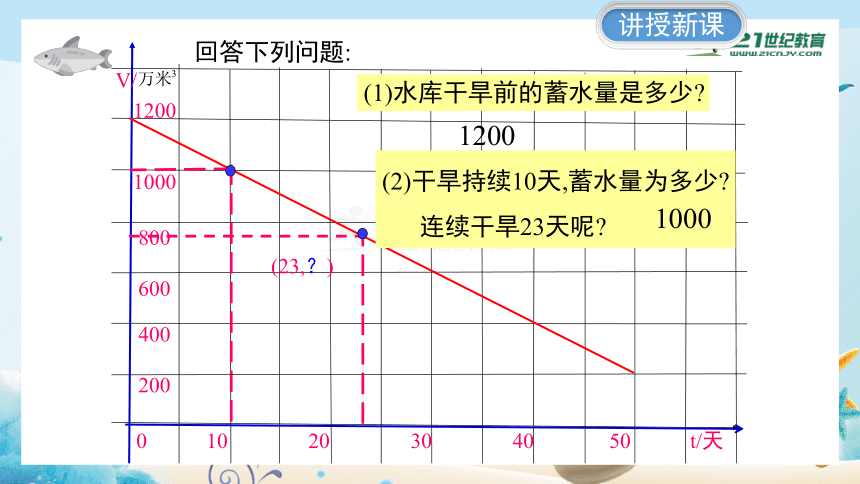
回答下列问题:
(2)干旱持续10天,蓄水量为多少
连续干旱23天呢
1000
(1)水库干旱前的蓄水量是多少
1200
1200
1000
800
600
400
200
(23,?)
讲授新课
0 10 20 30 40 50 t/天
V/
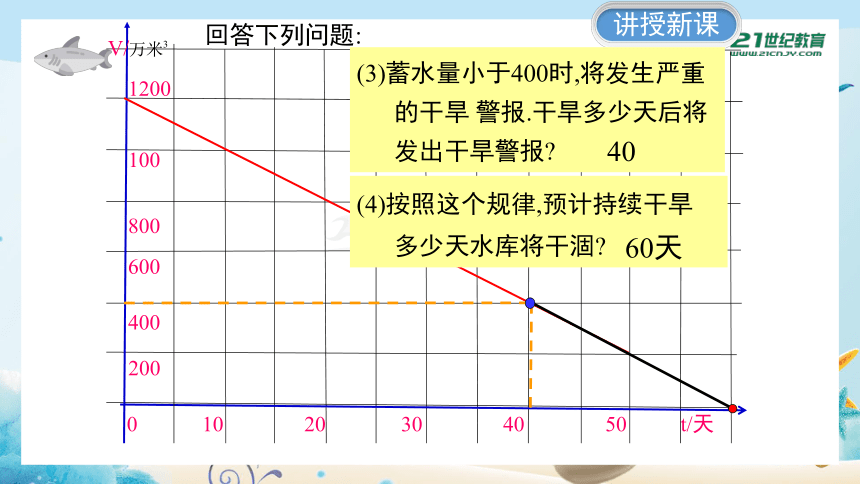
回答下列问题:
(3)蓄水量小于400时,将发生严重
的干旱 警报.干旱多少天后将
发出干旱警报
40
(4)按照这个规律,预计持续干旱
多少天水库将干涸
60天
1200
100
800
600
400
200
讲授新课
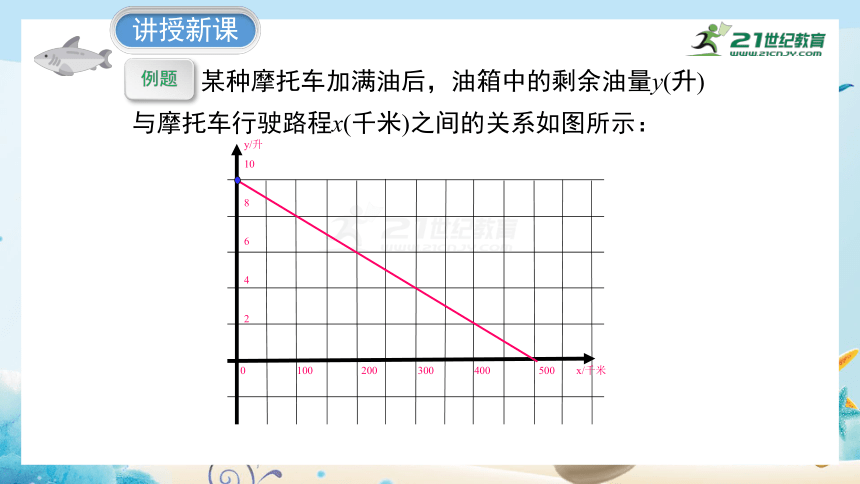
某种摩托车加满油后,油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图所示:
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
例题
讲授新课
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(1)油箱最多可储油多少升?
解:当 x=0时,y=10.因此,油箱最多可储油10L.
根据图象回答下列问题:
讲授新课
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(2)一箱汽油可供摩托车行驶多少千米?
解:当 y=0时, x=500,因此一箱汽油可供摩托车行驶500km.
讲授新课
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(3)摩托车每行驶100千米消耗多少升
解: x从100增加到200时, y从8减少到6,减少了2,因此摩托车每行驶100千米消耗2升汽油.
讲授新课
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(4)油箱中的剩余油量小于1升时将自动报警.行驶多少千米后,摩托车 将自动报警
解:当y=1时,x=450,因此行驶了450千米后,摩托车将自动报警.
讲授新课
总结归纳
如何解答实际情景函数图象的信息?
1.理解横纵坐标分别表示的的实际意义;
3.利用数形结合的思想:
将“数”转化为“形” 由“形”定“数”
2.分析已知条件,通过作x轴或y轴的垂线,在图象上找到对应的点,由点的横坐标或者纵坐标的值读出要求的值;
由于持续高温和连日无
雨,某水库的蓄水量随着
时间的增加而减少.干旱
持续时间t(天)与蓄水量V
(万米3)的关系如下图所示,
回答下列问题:
想一想
(2)干旱持续10天,蓄水
量为多少?连续干旱
23天呢?
(1)水库干旱前的蓄水
量是多少?
(3)蓄水量小于400万米3时,将
发生严重干旱警报.干旱多少
天后将发出严重干旱警报?
·
·
·
(4)按照这个规律,预计持续干旱多少天水库将干涸?
当得知周边地区的干旱情况后,育才学校的小明意识到节约用水的重要性,当天在班上倡议节约用水,得到全班乃至全校师生的积极响应。
从宣传活动开始,假设每天参加该活动的家庭数增加数量相同,最后全校师生都参加了活动,并且参加该活动的家庭数 S( 户)与宣传时间 t(天)的函数关系如图所示。
做一做
200
1000
20 t(天)
S(户)
·
0
·
·
·
(2)全校师生共有多少户?该活动
持续了几天?
(1)活动开始当天,全校有
多少户家庭参加了活动?
根据图象回答下列问题:
(3)你知道平均每天增加了多少户?
(200户)
(1000户,20天)
(40户)
200
1000
20 t(天)
S(户)
·
0
根据图象回答下列问题:
(4)活动第几天时,参加该活动的
家庭数达到800户?
(5)写出参加活动的家庭数S与活动
时间t之间的函数关系式。
(第15天)
( )
200
1000
20 t(天)
S(户)
·
0
1.如图,
(1)当y=0时,x=________ ;
(2)直线对应的函数表达式是______________.
深入探究
·
-2
一元一次方程0.5x+1=0与一次
函数y=0.5x+1有什么联系?
1.从“数”的方面看,当一次函数
y=0.5x+1的函数值y=0时,相应的
自变量的值即为方程0.5x+1=0解。
2.从“形”的方面看,函数y=0.5x+1
与x轴交点的横坐标,即为方程
0.5x+1=0的解。
2
0
1
3
1
2
3
-1
-2
-3
-1
x
y
议一议
课堂练习
1.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是 ( )
A.37.2分钟 B.48分钟
C.30分钟 D.33分钟
A
课堂练习
2. 小车沿一个斜坡下滑,它的速度v(m/s)与时间t(s)的关系如图所示,v与t之间的关系式是 ,下滑3 s时小车的速度是 .
v=2.5t
7.5 m/s
课堂练习
3.如图所示的折线ABC为某地出租车收费y(元)与乘坐路程x(千米)之间的函数关系图象,当x≥3时,该函数的解析式为 ,乘坐2千米时,
车费为 元,乘坐8千米时,车费为 元.
4.一元一次方程0.5x+1=0的解是一次函数y=0.5x+1的图象与 的横坐标.
y=x
3
8
x轴交点
课堂总结
本节课主要应掌握以下内容:
1.能通过函数图象获取信息.
2.能利用函数图象解决简单的实际问题.
3.初步体会方程与函数的关系.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
在一次函数y=kx+b中
当k>0 时,y 随x的增大而增大,
当b>0 时,直线交y轴于正半轴,
必过一、二、三象限;
当b<0 时,直线交y轴于负半轴,
必过一、三、四象限;
回顾与复习
在一次函数y=kx+b中
当k<0 时,y随x的增大而减小,
当b>0 时,直线交y轴于正半轴,
必过一、二、四象限;
当b<0 时,直线交y轴于负半轴,
必过二、三、四象限.
回顾与复习
4.4 一次函数的应用
第四章 一次函数
第2课时 借助单个一次函数图象解决简单实际问题
单个一次函数图象的应用
1.利用一次函数图象解决实际问题,关键是找到图象中两个变量之间的数量关系,把实际问题抽象、升华为一次函数模型,即建模,再利用一次函数的相关性质解决实际问题,常见类型如下:
(1) 题目中已知一次函数的关系式,可直接运用一
次函数的性质求解;
讲授新课
(2)题目中没有给出一次函数的关系式,而是通过语言、表格或图象给出一次函数的情境,这时需要先根据题目中给出的信息求出一次函数的关系式,再利用一次函数的性质解决实际问题.
2.要点精析:“建模”可以把实际问题转化为关于一次
函数的数学问题,它的关键是确定函数与自变量之间
的关系式,并确定实际问题中自变量的取值范围.
讲授新课
讲授新课
例题
由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.蓄水量V(万m3)与干旱持续时间 t( 天) 的关系如图所示,
讲授新课
0 10 20 30 40 50 t/天
V/
回答下列问题:
(2)干旱持续10天,蓄水量为多少
连续干旱23天呢
1000
(1)水库干旱前的蓄水量是多少
1200
1200
1000
800
600
400
200
(23,?)
讲授新课
0 10 20 30 40 50 t/天
V/
回答下列问题:
(3)蓄水量小于400时,将发生严重
的干旱 警报.干旱多少天后将
发出干旱警报
40
(4)按照这个规律,预计持续干旱
多少天水库将干涸
60天
1200
100
800
600
400
200
讲授新课
某种摩托车加满油后,油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图所示:
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
例题
讲授新课
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(1)油箱最多可储油多少升?
解:当 x=0时,y=10.因此,油箱最多可储油10L.
根据图象回答下列问题:
讲授新课
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(2)一箱汽油可供摩托车行驶多少千米?
解:当 y=0时, x=500,因此一箱汽油可供摩托车行驶500km.
讲授新课
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(3)摩托车每行驶100千米消耗多少升
解: x从100增加到200时, y从8减少到6,减少了2,因此摩托车每行驶100千米消耗2升汽油.
讲授新课
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(4)油箱中的剩余油量小于1升时将自动报警.行驶多少千米后,摩托车 将自动报警
解:当y=1时,x=450,因此行驶了450千米后,摩托车将自动报警.
讲授新课
总结归纳
如何解答实际情景函数图象的信息?
1.理解横纵坐标分别表示的的实际意义;
3.利用数形结合的思想:
将“数”转化为“形” 由“形”定“数”
2.分析已知条件,通过作x轴或y轴的垂线,在图象上找到对应的点,由点的横坐标或者纵坐标的值读出要求的值;
由于持续高温和连日无
雨,某水库的蓄水量随着
时间的增加而减少.干旱
持续时间t(天)与蓄水量V
(万米3)的关系如下图所示,
回答下列问题:
想一想
(2)干旱持续10天,蓄水
量为多少?连续干旱
23天呢?
(1)水库干旱前的蓄水
量是多少?
(3)蓄水量小于400万米3时,将
发生严重干旱警报.干旱多少
天后将发出严重干旱警报?
·
·
·
(4)按照这个规律,预计持续干旱多少天水库将干涸?
当得知周边地区的干旱情况后,育才学校的小明意识到节约用水的重要性,当天在班上倡议节约用水,得到全班乃至全校师生的积极响应。
从宣传活动开始,假设每天参加该活动的家庭数增加数量相同,最后全校师生都参加了活动,并且参加该活动的家庭数 S( 户)与宣传时间 t(天)的函数关系如图所示。
做一做
200
1000
20 t(天)
S(户)
·
0
·
·
·
(2)全校师生共有多少户?该活动
持续了几天?
(1)活动开始当天,全校有
多少户家庭参加了活动?
根据图象回答下列问题:
(3)你知道平均每天增加了多少户?
(200户)
(1000户,20天)
(40户)
200
1000
20 t(天)
S(户)
·
0
根据图象回答下列问题:
(4)活动第几天时,参加该活动的
家庭数达到800户?
(5)写出参加活动的家庭数S与活动
时间t之间的函数关系式。
(第15天)
( )
200
1000
20 t(天)
S(户)
·
0
1.如图,
(1)当y=0时,x=________ ;
(2)直线对应的函数表达式是______________.
深入探究
·
-2
一元一次方程0.5x+1=0与一次
函数y=0.5x+1有什么联系?
1.从“数”的方面看,当一次函数
y=0.5x+1的函数值y=0时,相应的
自变量的值即为方程0.5x+1=0解。
2.从“形”的方面看,函数y=0.5x+1
与x轴交点的横坐标,即为方程
0.5x+1=0的解。
2
0
1
3
1
2
3
-1
-2
-3
-1
x
y
议一议
课堂练习
1.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是 ( )
A.37.2分钟 B.48分钟
C.30分钟 D.33分钟
A
课堂练习
2. 小车沿一个斜坡下滑,它的速度v(m/s)与时间t(s)的关系如图所示,v与t之间的关系式是 ,下滑3 s时小车的速度是 .
v=2.5t
7.5 m/s
课堂练习
3.如图所示的折线ABC为某地出租车收费y(元)与乘坐路程x(千米)之间的函数关系图象,当x≥3时,该函数的解析式为 ,乘坐2千米时,
车费为 元,乘坐8千米时,车费为 元.
4.一元一次方程0.5x+1=0的解是一次函数y=0.5x+1的图象与 的横坐标.
y=x
3
8
x轴交点
课堂总结
本节课主要应掌握以下内容:
1.能通过函数图象获取信息.
2.能利用函数图象解决简单的实际问题.
3.初步体会方程与函数的关系.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
