4.4.1 一次函数的应用 课件(共25张PPT)
文档属性
| 名称 | 4.4.1 一次函数的应用 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 19:35:29 | ||
图片预览








文档简介
(共25张PPT)
1.什么是一次函数
2.一次函数的图象是什么?
3.一次函数具有什么性质?
若两个变量x,y间的关系式可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数.
一条直线
复习回顾
4.4 一次函数的应用
第四章 一次函数
第1课时 借助一次函数表达式解决一些简单问题
1.了解两个条件可以确定一个一次函数,一个条件可以确定一个正比例函数,并能由此求出表达式.
2.会用待定系数法解决简单的实际问题.
3.能根据函数的图象确定一次函数的表达式.
讲授新课
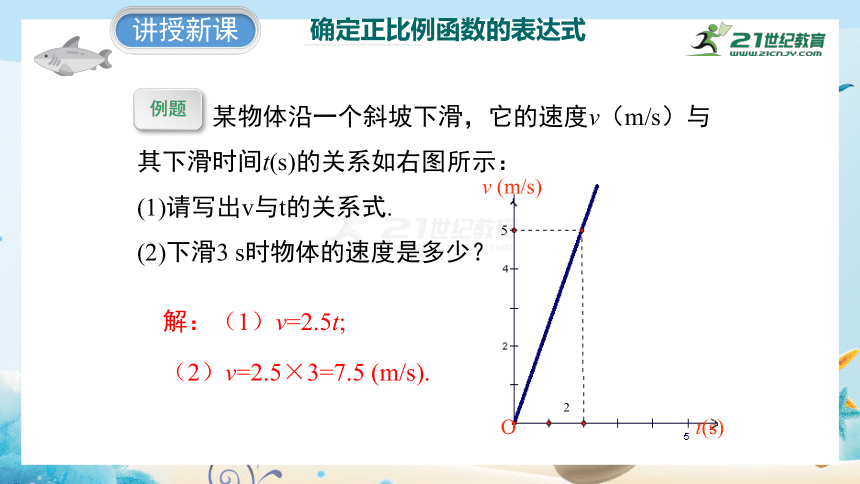
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如右图所示:
(1)请写出v与t的关系式.
(2)下滑3 s时物体的速度是多少?
v (m/s)
t(s)
O
解:(1)v=2.5t;
(2)v=2.5×3=7.5 (m/s).
5
2
确定正比例函数的表达式
例题
讲授新课
已知y与2x成正比例,且当x=3时,y=12,求y
与x的函数表达式.
导引:紧扣待定系数法的步骤,设出正比例函数的关
系式,利用一对对应值或图象上一个点的坐标
解决问题.
解: 设y=k·2x(k≠0).
因为当x=3时,y=12,
所以12=2×3×k.所以k=2.
所以所求的函数表达式为y=4x.
例题
讲授新课
想一想:确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
一个
两个
讲授新课
已知一次函数的图象经过(0,5)、(2,-5)两点,求一次函数的表达式.
解:设一次函数的表达式为y=kx+b,根据题意得,
∴-5=2k+b,5=b,
解得b=5,k=-5.
∴一次函数的表达式为y=-5x+5.
确定一次函数的表达式
例题
讲授新课
解:设直线l为y=kx+b,
∵l与直线y=-2x平行,∴k= -2.
又∵直线过点(0,2),
∴2=-2×0+b,
∴b=2,
∴直线l的表达式为y=-2x+2.
已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l的表达式.
练一练
讲授新课
如图,直线l是一次函数y=kx+b(k≠0)的图象.
求:(1)直线l对应的函数表达式;
(2)当y=2时,x的值.
导引: 紧扣待定系数法的步骤,利用点的坐标与
函数关系式之间的关系求出待
定的系数解决问题.
例题
讲授新课
解:(1)由图可知,直线l经过点(-2,0)和点(0,3),
将其坐标分别代入函数表达式y=kx+b,
得到-2k+b=0,b=3.
解得k= ,则直线l对应的函数表达式为
y= x+3.
(2)当y=2时,有2= x+3,解得x=- .
讲授新课
总 结
求一次函数的表达式都要经过设、列、解、还原四步,设都相同,就是设出一次函数的表达式,列就是把已知两点的坐标代入所设表达式,列出两个一次方程, 解这两个方程,将所求得的系数的值代回所设表达式 即可.
讲授新课
正比例函数与一次函数的图象如图所示,它们的交点为A(4,3),B为一次函数的图象与y轴的交点,且OA=2OB.求正比例函数与一次函数的表达式.
解:设正比例函数的表达式为y1=k1x,一次函数的表达式为y2=k2x+b.
∵点A(4,3)是它们的交点,
∴代入上述表达式中,
得3=4k1,3=4k2+b.
∴k1= ,
即正比例函数的表达式为y= x.
例题
讲授新课
∵OA= =5,且OA=2OB,
∴OB= .
∵点B在y轴的负半轴上,
∴B点的坐标为(0,- ).
又∵点B在一次函数y2=k2x+b的图象上,
∴- =b,
代入3=4k2+b中,得k2= .
∴一次函数的表达式为y2= x- .
讲授新课
如图,直线y= x+ 与两坐标轴分别交于
A,B两点.
(1)求AB的长;
(2)过A的直线l交x轴正半轴于
C,AB=AC,求直线l对应
的函数表达式.
做一做
讲授新课
(1) 对于直线y= x+ ,
令x=0,则y= ,
令y=0,则x=-1,
所以点A的坐标为(0, ),
点B的坐标为(-1,0).
所以AO= ,BO=1,
在Rt△ABO中,
AB=
解:
讲授新课
(2)在△ABC中,
因为AB=AC,AO⊥BC,
所以BO=CO.
所以C点的坐标为(1,0).
设直线l对应的函数表达式为y=kx+b(k,b为常数),
则b= ,且k+b=0,
解得k=- ,b= .
即直线l对应的函数表达式为y=- x+ .
解:
讲授新课
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作
几小时?
y = -5x + 40.
8 h
例题
讲授新课
根据图象确定一次函数的表达式的方法:从图象上选取两个已知点的坐标,然后运用待定系数法将两点的横、纵坐标代入所设表达式中求出待定系数,从而求出函数的表达式.
归纳总结
1. 已知四条直线y=kx-3,y=-1,
y=3和x=1所围成的四边形的面积是12,则k的值
为( )
A.1或-2 B.2或-1 C.3 D.4
A
2.若一次函数y=3x-b的图象经过点P(1,-1),则该函数
图象必经过点( )
A.(-1,1) B.(2,2) C.(-2,2) D (2,一2)
B
3.在一次函数 中,当 时 ,则 的
值为( )
A.-1 B.1 C.5 D.-5
B
4.若一次函数 y=kx+3的图象经过点(-1,2),则k=____.
1
5.根据如图所示的条件,写出直线的表达
式 、 .
y=2x
6.某同学在做放水实验时,记录下池中水量y(m3)与
放水时间 x (h)之间有如下对应关系 :
x … 2 4 6 …
y … 15 12 9 6 …
(1)按规律把表格填写完整:
(2)池中原有水__m3.
8
18
本节课我们主要学习了根据已知条件,如何求函数的表达式:
1.设函数表达式.
2.根据已知条件列出有关k, b的方程.
3.解方程,求k,b.
4.把k,b 代回表达式,写出表达式.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.什么是一次函数
2.一次函数的图象是什么?
3.一次函数具有什么性质?
若两个变量x,y间的关系式可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数.
一条直线
复习回顾
4.4 一次函数的应用
第四章 一次函数
第1课时 借助一次函数表达式解决一些简单问题
1.了解两个条件可以确定一个一次函数,一个条件可以确定一个正比例函数,并能由此求出表达式.
2.会用待定系数法解决简单的实际问题.
3.能根据函数的图象确定一次函数的表达式.
讲授新课
某物体沿一个斜坡下滑,它的速度v(m/s)与其下滑时间t(s)的关系如右图所示:
(1)请写出v与t的关系式.
(2)下滑3 s时物体的速度是多少?
v (m/s)
t(s)
O
解:(1)v=2.5t;
(2)v=2.5×3=7.5 (m/s).
5
2
确定正比例函数的表达式
例题
讲授新课
已知y与2x成正比例,且当x=3时,y=12,求y
与x的函数表达式.
导引:紧扣待定系数法的步骤,设出正比例函数的关
系式,利用一对对应值或图象上一个点的坐标
解决问题.
解: 设y=k·2x(k≠0).
因为当x=3时,y=12,
所以12=2×3×k.所以k=2.
所以所求的函数表达式为y=4x.
例题
讲授新课
想一想:确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
一个
两个
讲授新课
已知一次函数的图象经过(0,5)、(2,-5)两点,求一次函数的表达式.
解:设一次函数的表达式为y=kx+b,根据题意得,
∴-5=2k+b,5=b,
解得b=5,k=-5.
∴一次函数的表达式为y=-5x+5.
确定一次函数的表达式
例题
讲授新课
解:设直线l为y=kx+b,
∵l与直线y=-2x平行,∴k= -2.
又∵直线过点(0,2),
∴2=-2×0+b,
∴b=2,
∴直线l的表达式为y=-2x+2.
已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l的表达式.
练一练
讲授新课
如图,直线l是一次函数y=kx+b(k≠0)的图象.
求:(1)直线l对应的函数表达式;
(2)当y=2时,x的值.
导引: 紧扣待定系数法的步骤,利用点的坐标与
函数关系式之间的关系求出待
定的系数解决问题.
例题
讲授新课
解:(1)由图可知,直线l经过点(-2,0)和点(0,3),
将其坐标分别代入函数表达式y=kx+b,
得到-2k+b=0,b=3.
解得k= ,则直线l对应的函数表达式为
y= x+3.
(2)当y=2时,有2= x+3,解得x=- .
讲授新课
总 结
求一次函数的表达式都要经过设、列、解、还原四步,设都相同,就是设出一次函数的表达式,列就是把已知两点的坐标代入所设表达式,列出两个一次方程, 解这两个方程,将所求得的系数的值代回所设表达式 即可.
讲授新课
正比例函数与一次函数的图象如图所示,它们的交点为A(4,3),B为一次函数的图象与y轴的交点,且OA=2OB.求正比例函数与一次函数的表达式.
解:设正比例函数的表达式为y1=k1x,一次函数的表达式为y2=k2x+b.
∵点A(4,3)是它们的交点,
∴代入上述表达式中,
得3=4k1,3=4k2+b.
∴k1= ,
即正比例函数的表达式为y= x.
例题
讲授新课
∵OA= =5,且OA=2OB,
∴OB= .
∵点B在y轴的负半轴上,
∴B点的坐标为(0,- ).
又∵点B在一次函数y2=k2x+b的图象上,
∴- =b,
代入3=4k2+b中,得k2= .
∴一次函数的表达式为y2= x- .
讲授新课
如图,直线y= x+ 与两坐标轴分别交于
A,B两点.
(1)求AB的长;
(2)过A的直线l交x轴正半轴于
C,AB=AC,求直线l对应
的函数表达式.
做一做
讲授新课
(1) 对于直线y= x+ ,
令x=0,则y= ,
令y=0,则x=-1,
所以点A的坐标为(0, ),
点B的坐标为(-1,0).
所以AO= ,BO=1,
在Rt△ABO中,
AB=
解:
讲授新课
(2)在△ABC中,
因为AB=AC,AO⊥BC,
所以BO=CO.
所以C点的坐标为(1,0).
设直线l对应的函数表达式为y=kx+b(k,b为常数),
则b= ,且k+b=0,
解得k=- ,b= .
即直线l对应的函数表达式为y=- x+ .
解:
讲授新课
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作
几小时?
y = -5x + 40.
8 h
例题
讲授新课
根据图象确定一次函数的表达式的方法:从图象上选取两个已知点的坐标,然后运用待定系数法将两点的横、纵坐标代入所设表达式中求出待定系数,从而求出函数的表达式.
归纳总结
1. 已知四条直线y=kx-3,y=-1,
y=3和x=1所围成的四边形的面积是12,则k的值
为( )
A.1或-2 B.2或-1 C.3 D.4
A
2.若一次函数y=3x-b的图象经过点P(1,-1),则该函数
图象必经过点( )
A.(-1,1) B.(2,2) C.(-2,2) D (2,一2)
B
3.在一次函数 中,当 时 ,则 的
值为( )
A.-1 B.1 C.5 D.-5
B
4.若一次函数 y=kx+3的图象经过点(-1,2),则k=____.
1
5.根据如图所示的条件,写出直线的表达
式 、 .
y=2x
6.某同学在做放水实验时,记录下池中水量y(m3)与
放水时间 x (h)之间有如下对应关系 :
x … 2 4 6 …
y … 15 12 9 6 …
(1)按规律把表格填写完整:
(2)池中原有水__m3.
8
18
本节课我们主要学习了根据已知条件,如何求函数的表达式:
1.设函数表达式.
2.根据已知条件列出有关k, b的方程.
3.解方程,求k,b.
4.把k,b 代回表达式,写出表达式.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
