新人教版七年级上册1.5有理数的乘方
文档属性
| 名称 | 新人教版七年级上册1.5有理数的乘方 |

|
|
| 格式 | zip | ||
| 文件大小 | 68.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-19 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
有理数的乘方
活动一:
以两人小组的方式,拿一张信纸(约0.1毫米)依次对折一次,两次,三次,四次……
探究1:观察纸张的层数、厚度所发生的变化
探究2:把足够长的厚0.1毫米的信纸继续折叠20次、30次,会有多少层,有多厚?
探究一:
对折一次2层,即2
对折两次4层,即2×2,记作22,读作2的平方(或2的2次方)
对折三次8层,即2×2×2,记作23,读作2的立方(或2的3次方)
对折四次16层,即2×2×2×2,记作__,读作_____
对折20次,对折n次,又如何记,如何读?
推广:
将数字换成字母,如aaa‥‥a(n个a相乘,n为正整数),又如何记 由此出现一种新的运算_____
计算并思考:
相同因数的乘法如何简化
10×10×10=
-3×3 ×3×3=
(-3)×(-3)×(-3)×(-3)=
-(-5) (-5) (-5) (-5)=
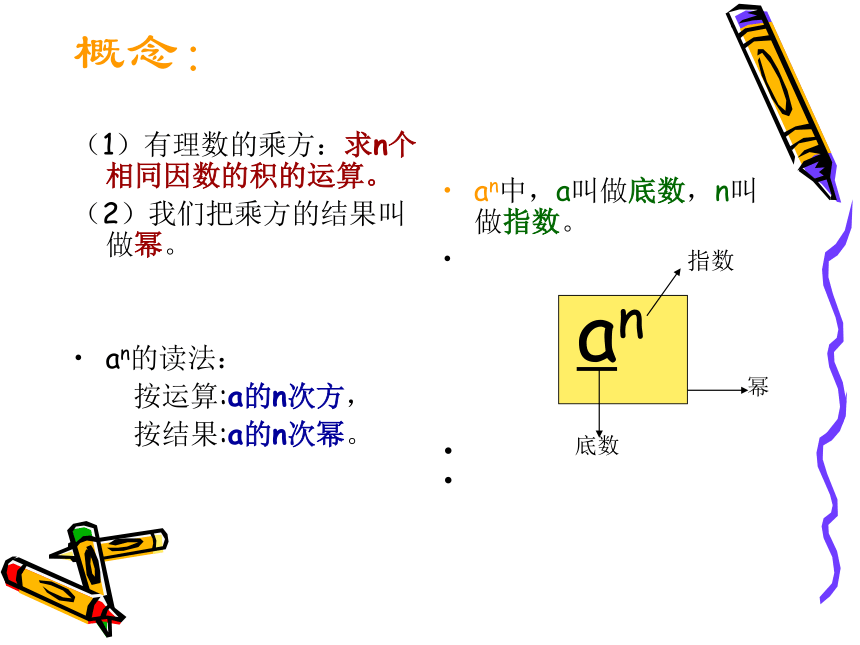
概念:
(1)有理数的乘方:求n个相同因数的积的运算。
(2)我们把乘方的结果叫做幂。
an的读法:
按运算:a的n次方,
按结果:a的n次幂。
an中,a叫做底数,n叫做指数。
指数
an
幂
底数
反馈练习:
(1)(—5)5 读作什么?它的底数和指数分别是什么?
(2)(-4)(-4)(-4)(-4)写成乘方的形式是什么?它的底数和指数分别是什么?
(3)5有没有指数?如果有,是多少?
例1 计算:
(1) (-4)3
(2) 23
(3) 09
(4) (-2)4
(5) -24
探究:
1.乘方和乘法之间有何关系?
2.我们可把乘方运算转化为什么运算来计算?注意(—2)4 与—24的区别。
3.由例1你发现负数的幂的正负有什么规律
当指数是___时,负数的幂是___数.
当指数是___时,负数的幂是___数.
双基练习
1.口答P51练习
2.计算:(-5)4=___; -54=____;
(-2×3)2=____; -2×32=____;
-(-2)3=____; -(-3)2=____
3.一个数的立方等于它本身,这个数是( )
A.1 B.-1,1 C.0 D.-1,1,0
4.是任意有理数,下列说法正确是的( )
A.(a+1)2的值总是正的 B.a2+1的值总是正的
C.-(a+1)3的值总是负数 D.a2+1的值中,最大值是0
求几个相同因数的积:
n 1 2 3 4 5…
2n 2 4 8 16 32…
(-2)n -2 4 -8 16 -32…
观察思考:
①表格中指数分别是奇数时,幂是怎样变化的 指数是偶数时呢
②平方是4的数有几个?分别是?
归纳总结:
幂的符号运算法则:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;零的非零次幂都是零。
当x2是正数时,那么x有___个
深化练习:
1、当n为正整数时,(1)(-a)2n=___a2n,(2)(-a)2n-1=___a2n-1,(3)10n展开后1后面有___个0。
2、填“>”“<”或“=”
(1)若a<0,则a2___0,a3___0.
(2)若an = 0,则a___0(n为正整数)
(3)若a7>0,则a___0
活动2:
1米长的木棒,第一次截去一半,第二次截去剩下的一半,如此截下去,第七次剩下的小棒有多长?
n 1 2 3 4 5 6 7...
1/8 1/16 1/32 1/64 1/128
感受:
底数大于1时:乘方运算的结果增长得很快。
底数大于零而小于1时:乘方运算的结果减小得很快。
想入非非:
如果一层楼按高3米计算,把足够长的厚0.1毫米的纸继续折叠20次有104米高,有34层楼高;继续折叠30次后有10万多米高,有12个珠穆朗玛峰高。
220=1048576
1048576×0.1毫米=104.8576米
230=1073741824
1073741824×0.1毫米=107374.1824米
数学乐园:
古时候,在一个王国里有一位聪明的大臣发明了国际象棋并献给了国王。国王从此迷上了下棋。为了向聪明的大臣表示感谢,国王答应满足大臣的一个要求。大臣说:“就在这个棋盘上放上些米粒吧。第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格。”“你真傻!就要这么一点米粒?!”国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”你认为国王的国库里有这么多米吗?
回顾思考及作业:
1.本节课你学到了什么?
2.本节课你有什么感受?还有什么困惑?
布置作业:
1.教材第56页第1题。
2.搜集生活中运用乘方的实例。
课外练习
1.计算:(2/3)2003×(-3/2)2004
2.计算:(-2)2004+(-2)2005=
3.若(a-2)2+(b-5)2=0,则(-a)5b5=___
有理数的乘方
活动一:
以两人小组的方式,拿一张信纸(约0.1毫米)依次对折一次,两次,三次,四次……
探究1:观察纸张的层数、厚度所发生的变化
探究2:把足够长的厚0.1毫米的信纸继续折叠20次、30次,会有多少层,有多厚?
探究一:
对折一次2层,即2
对折两次4层,即2×2,记作22,读作2的平方(或2的2次方)
对折三次8层,即2×2×2,记作23,读作2的立方(或2的3次方)
对折四次16层,即2×2×2×2,记作__,读作_____
对折20次,对折n次,又如何记,如何读?
推广:
将数字换成字母,如aaa‥‥a(n个a相乘,n为正整数),又如何记 由此出现一种新的运算_____
计算并思考:
相同因数的乘法如何简化
10×10×10=
-3×3 ×3×3=
(-3)×(-3)×(-3)×(-3)=
-(-5) (-5) (-5) (-5)=
概念:
(1)有理数的乘方:求n个相同因数的积的运算。
(2)我们把乘方的结果叫做幂。
an的读法:
按运算:a的n次方,
按结果:a的n次幂。
an中,a叫做底数,n叫做指数。
指数
an
幂
底数
反馈练习:
(1)(—5)5 读作什么?它的底数和指数分别是什么?
(2)(-4)(-4)(-4)(-4)写成乘方的形式是什么?它的底数和指数分别是什么?
(3)5有没有指数?如果有,是多少?
例1 计算:
(1) (-4)3
(2) 23
(3) 09
(4) (-2)4
(5) -24
探究:
1.乘方和乘法之间有何关系?
2.我们可把乘方运算转化为什么运算来计算?注意(—2)4 与—24的区别。
3.由例1你发现负数的幂的正负有什么规律
当指数是___时,负数的幂是___数.
当指数是___时,负数的幂是___数.
双基练习
1.口答P51练习
2.计算:(-5)4=___; -54=____;
(-2×3)2=____; -2×32=____;
-(-2)3=____; -(-3)2=____
3.一个数的立方等于它本身,这个数是( )
A.1 B.-1,1 C.0 D.-1,1,0
4.是任意有理数,下列说法正确是的( )
A.(a+1)2的值总是正的 B.a2+1的值总是正的
C.-(a+1)3的值总是负数 D.a2+1的值中,最大值是0
求几个相同因数的积:
n 1 2 3 4 5…
2n 2 4 8 16 32…
(-2)n -2 4 -8 16 -32…
观察思考:
①表格中指数分别是奇数时,幂是怎样变化的 指数是偶数时呢
②平方是4的数有几个?分别是?
归纳总结:
幂的符号运算法则:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;零的非零次幂都是零。
当x2是正数时,那么x有___个
深化练习:
1、当n为正整数时,(1)(-a)2n=___a2n,(2)(-a)2n-1=___a2n-1,(3)10n展开后1后面有___个0。
2、填“>”“<”或“=”
(1)若a<0,则a2___0,a3___0.
(2)若an = 0,则a___0(n为正整数)
(3)若a7>0,则a___0
活动2:
1米长的木棒,第一次截去一半,第二次截去剩下的一半,如此截下去,第七次剩下的小棒有多长?
n 1 2 3 4 5 6 7...
1/8 1/16 1/32 1/64 1/128
感受:
底数大于1时:乘方运算的结果增长得很快。
底数大于零而小于1时:乘方运算的结果减小得很快。
想入非非:
如果一层楼按高3米计算,把足够长的厚0.1毫米的纸继续折叠20次有104米高,有34层楼高;继续折叠30次后有10万多米高,有12个珠穆朗玛峰高。
220=1048576
1048576×0.1毫米=104.8576米
230=1073741824
1073741824×0.1毫米=107374.1824米
数学乐园:
古时候,在一个王国里有一位聪明的大臣发明了国际象棋并献给了国王。国王从此迷上了下棋。为了向聪明的大臣表示感谢,国王答应满足大臣的一个要求。大臣说:“就在这个棋盘上放上些米粒吧。第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格。”“你真傻!就要这么一点米粒?!”国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”你认为国王的国库里有这么多米吗?
回顾思考及作业:
1.本节课你学到了什么?
2.本节课你有什么感受?还有什么困惑?
布置作业:
1.教材第56页第1题。
2.搜集生活中运用乘方的实例。
课外练习
1.计算:(2/3)2003×(-3/2)2004
2.计算:(-2)2004+(-2)2005=
3.若(a-2)2+(b-5)2=0,则(-a)5b5=___
