北师大版(2019)数学-必修第二册-第一章 三角函数-§7.3 正切函数的图象与性质PPT(共23张ppt)
文档属性
| 名称 | 北师大版(2019)数学-必修第二册-第一章 三角函数-§7.3 正切函数的图象与性质PPT(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
§7.3 正切函数的图象与性质
正切函数在实际测量中的应用是十分广泛的,例如,测量山的高度、测量池塘的宽度都需要利用正切函数进行解决.同学们,你能够类比研究正弦函数和余弦函数的方法,研究正切函数的图象和性质吗
三角函数包括正、余弦函数和正切函数,我们已经研究了正、余弦函数的图象和性质, 因此, 进一步研究正切函数的性质与图象就成为学习的必然.
1.能画出y=tan x,x≠+kπ,k∈Z的图象.
2.理解正切函数的定义域、值域、周期性、奇偶性,及其在区间内的单调性.
1.通过正切曲线的学习,培养数学抽象素养.
2.通过正切函数的图象与性质的应用,培养数学运算与逻辑推理素养.
课标要求
素养要求
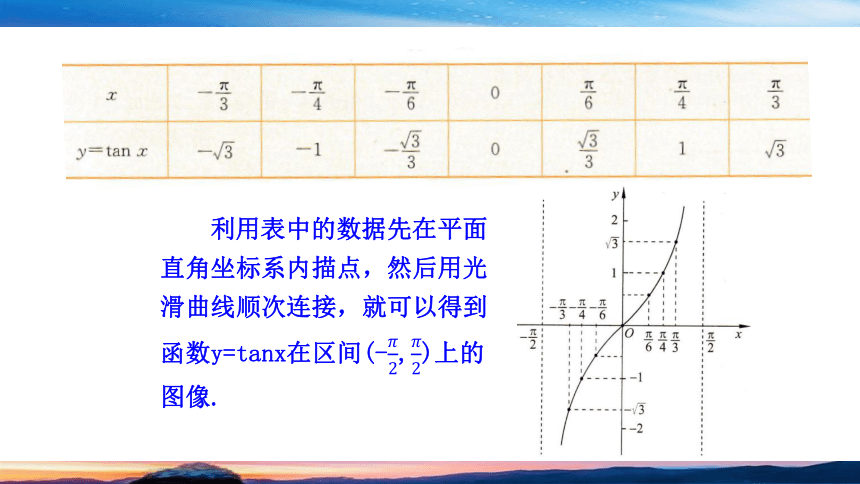
类比画正弦函数图像的方法,首先画出函数y=tanx,x∈(-,)的图像,再利用周期性将其延拓到整个定义域上,为此只需在区间(-,)上取一系列的x值,列表.
探究点1 正切函数的图象
利用表中的数据先在平面直角坐标系内描点,然后用光滑曲线顺次连接,就可以得到函数y=tanx在区间(-,)上的图像.
因为正切函数y=tanx是以π为周期的函数,所以它在区间(kπ-,kπ+),k∈Z,k≠0上与在区间(-,)上的函数图像形状完全相同.函数y=tanx,x∈(-,)上的图象向左、右平移就可以得到正切函数y=tanx在{x∈R|x≠}上的图像,正切函数的图像称为正切曲线.
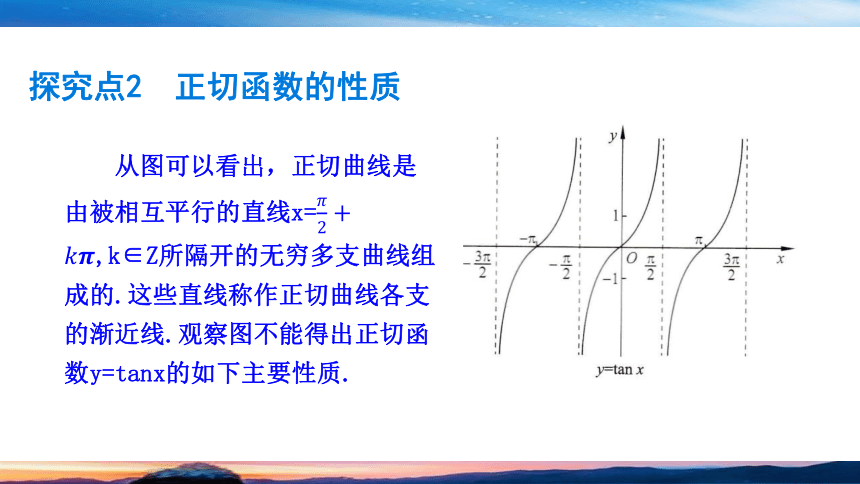
从图可以看出,正切曲线是由被相互平行的直线x=,k∈Z所隔开的无穷多支曲线组成的.这些直线称作正切曲线各支的渐近线.观察图不能得出正切函数y=tanx的如下主要性质.
探究点2 正切函数的性质
1.定义域
正切函数的定义域是{x∈R|x≠}.
2.值域
当x从左侧趋近时,tanx趋近正无穷大;
当x从右侧趋近-时,tanx趋近负无穷大.即y=tanx的值域是实数集R.
3.周期性
正切函数是周期函数,周期是,k≠0,最小正周期是π.
4.奇偶性
由tan(-x)=-tanx可知,正切函数是奇函数,正切曲线关于原点对称,(,0)都是它的对称中心.
5.单调性
正切函数在每一个区间(-),上单调递增.
例4 画出下列函数的图象,并求出定义域、周期和单调区间:
⑴ y=tan2x; ⑵ y=tan(x-).
解 ⑴画出y=tan2x的图像,如图,由y=tanx的定义域可知,函数y=tan2x的自变量x应满足2x≠,,即x≠,.
所以函数的定义域是{x∈R|x≠,}.
由于y=tanx的周期是π,因此函数y=tan2x的最小正周期是.
因为y=tanx的单调递增区间是(-),.
所以由-,.
解得-,.
因此函数y=tan2x的单调递增区间是(-),.
⑵画出y=tan(x-)的图像,如图,由y=tanx的定义可知函数y=tan(x-)的自变量应满足x-≠,,即x≠,.因此,函数y=tan(x-)的定义域是{x∈R|x≠,}.
由于tan(x-)=tan(x-+π)=tan[(x+π)-],因此函数y=tan(x-)的最小正周期是π.
由-,,解得-,.
如此函数的单调递增区间是(-),.
例5 比较下列各组中三角函数的值的大小:
⑴ tan(-)与tan; ⑵ tan(-)与tan(-).
解 ⑴ tan(-)=-tan=-tan(-+π)=-(-tan)=tan,
tan=tan(+π)=tan.
由于y=tanx在区间(0,)上单调递增,因0<<<,因此tan即 tan(-)⑵tan(-)=-tan=-tan(3π+)=-tan,
tan(-)=-tan=-tan(+3π)=-tan.
由于y=tanx在区间(0,)上单调递增,因0<<<,
因此tan即tan(-)>tan.
C
A
2.函数y=tanx(-≤x≤)的值域是( )
A. [-1,1] B.(-∞,-1]∪[1,+∞) C.(-∞,1] D.[-1,+∞)
解析 函数y=tanx在区间[-,]上单调递增,tan(-)=-1,tan=1.
被人揭下面具是一种失败,自己揭下面具却是一种胜利.
——雨果
§7.3 正切函数的图象与性质
正切函数在实际测量中的应用是十分广泛的,例如,测量山的高度、测量池塘的宽度都需要利用正切函数进行解决.同学们,你能够类比研究正弦函数和余弦函数的方法,研究正切函数的图象和性质吗
三角函数包括正、余弦函数和正切函数,我们已经研究了正、余弦函数的图象和性质, 因此, 进一步研究正切函数的性质与图象就成为学习的必然.
1.能画出y=tan x,x≠+kπ,k∈Z的图象.
2.理解正切函数的定义域、值域、周期性、奇偶性,及其在区间内的单调性.
1.通过正切曲线的学习,培养数学抽象素养.
2.通过正切函数的图象与性质的应用,培养数学运算与逻辑推理素养.
课标要求
素养要求
类比画正弦函数图像的方法,首先画出函数y=tanx,x∈(-,)的图像,再利用周期性将其延拓到整个定义域上,为此只需在区间(-,)上取一系列的x值,列表.
探究点1 正切函数的图象
利用表中的数据先在平面直角坐标系内描点,然后用光滑曲线顺次连接,就可以得到函数y=tanx在区间(-,)上的图像.
因为正切函数y=tanx是以π为周期的函数,所以它在区间(kπ-,kπ+),k∈Z,k≠0上与在区间(-,)上的函数图像形状完全相同.函数y=tanx,x∈(-,)上的图象向左、右平移就可以得到正切函数y=tanx在{x∈R|x≠}上的图像,正切函数的图像称为正切曲线.
从图可以看出,正切曲线是由被相互平行的直线x=,k∈Z所隔开的无穷多支曲线组成的.这些直线称作正切曲线各支的渐近线.观察图不能得出正切函数y=tanx的如下主要性质.
探究点2 正切函数的性质
1.定义域
正切函数的定义域是{x∈R|x≠}.
2.值域
当x从左侧趋近时,tanx趋近正无穷大;
当x从右侧趋近-时,tanx趋近负无穷大.即y=tanx的值域是实数集R.
3.周期性
正切函数是周期函数,周期是,k≠0,最小正周期是π.
4.奇偶性
由tan(-x)=-tanx可知,正切函数是奇函数,正切曲线关于原点对称,(,0)都是它的对称中心.
5.单调性
正切函数在每一个区间(-),上单调递增.
例4 画出下列函数的图象,并求出定义域、周期和单调区间:
⑴ y=tan2x; ⑵ y=tan(x-).
解 ⑴画出y=tan2x的图像,如图,由y=tanx的定义域可知,函数y=tan2x的自变量x应满足2x≠,,即x≠,.
所以函数的定义域是{x∈R|x≠,}.
由于y=tanx的周期是π,因此函数y=tan2x的最小正周期是.
因为y=tanx的单调递增区间是(-),.
所以由-,.
解得-,.
因此函数y=tan2x的单调递增区间是(-),.
⑵画出y=tan(x-)的图像,如图,由y=tanx的定义可知函数y=tan(x-)的自变量应满足x-≠,,即x≠,.因此,函数y=tan(x-)的定义域是{x∈R|x≠,}.
由于tan(x-)=tan(x-+π)=tan[(x+π)-],因此函数y=tan(x-)的最小正周期是π.
由-,,解得-,.
如此函数的单调递增区间是(-),.
例5 比较下列各组中三角函数的值的大小:
⑴ tan(-)与tan; ⑵ tan(-)与tan(-).
解 ⑴ tan(-)=-tan=-tan(-+π)=-(-tan)=tan,
tan=tan(+π)=tan.
由于y=tanx在区间(0,)上单调递增,因0<<<,因此tan
tan(-)=-tan=-tan(+3π)=-tan.
由于y=tanx在区间(0,)上单调递增,因0<<<,
因此tan
C
A
2.函数y=tanx(-≤x≤)的值域是( )
A. [-1,1] B.(-∞,-1]∪[1,+∞) C.(-∞,1] D.[-1,+∞)
解析 函数y=tanx在区间[-,]上单调递增,tan(-)=-1,tan=1.
被人揭下面具是一种失败,自己揭下面具却是一种胜利.
——雨果
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
