北师大版(2019)数学-必修第二册-第一章 三角函数-§5.2余弦函数的图象与性质再认识 课件(共30张PPT)
文档属性
| 名称 | 北师大版(2019)数学-必修第二册-第一章 三角函数-§5.2余弦函数的图象与性质再认识 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
§5.2余弦函数的图象与性质再认识
图象的平移变换(a>0,b>0)
向上平移 b个单位长度
向下平移 b个单位长度
f(x)
向左平移a个单位长度
向右平移a个单位长度
f(x)-b
f(x)+b
f(x+a)
f(x-a)
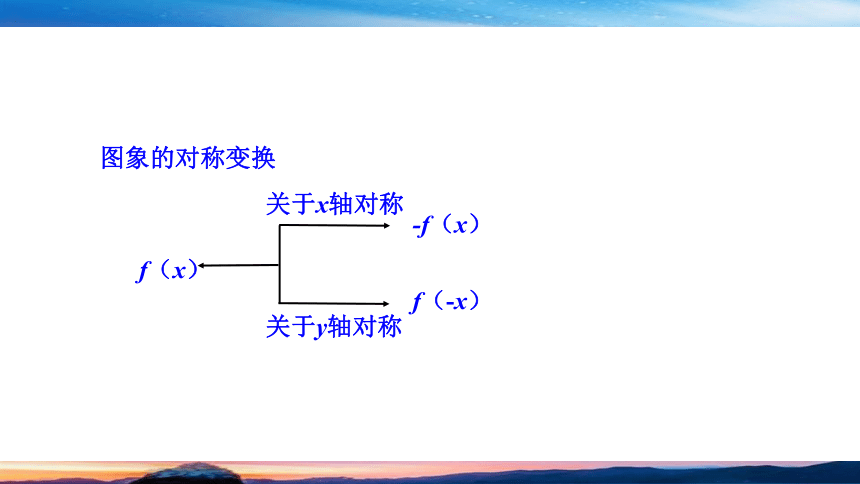
图象的对称变换
f(x)
关于x轴对称
-f(x)
f(-x)
关于y轴对称
1.能正确使用“五点法”、“图象变换法”画出余弦函数的简图2.掌握余弦函数的性质,会求余弦函数的最小正周期,单调区间和最值.
1.通过画余弦函数的图象,培养直观想象素养.
2.通过余弦函数的性质的应用,培养数学运算素养.
课标要求
素养要求
在区间[0,2π]上取一系列的x值,例如0, , , ,··· , 2π列表(如表).
探究点1 余弦函数的图象
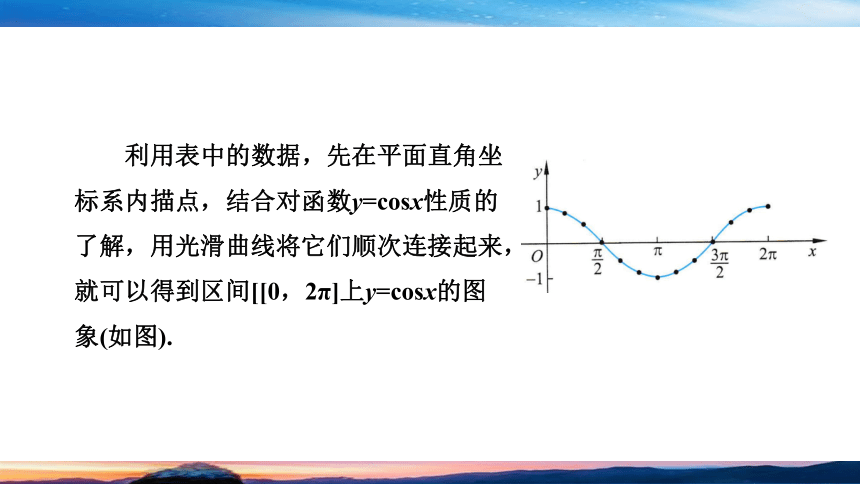
利用表中的数据,先在平面直角坐标系内描点,结合对函数y=cosx性质的了解,用光滑曲线将它们顺次连接起来,就可以得到区间[[0,2π]上y=cosx的图象(如图).
由周期性可知,函数y=cosx在区间[2kπ, 2(k+1)π],k∈Z,k≠0上与在区间[0, 2π]上的函数图象形状完全相同,只是位置不同,将函数y=cosx,x ∈[0, 2π]的图象向左、右平移(每次平移2π个单位长度),就可以得到余弦函数y=cosx,x ∈R的图象(如图).
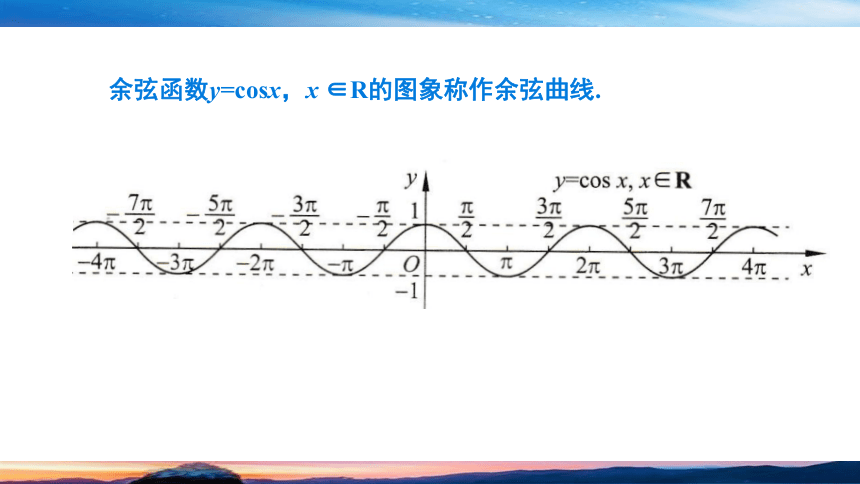
余弦函数y=cosx,x ∈R的图象称作余弦曲线.
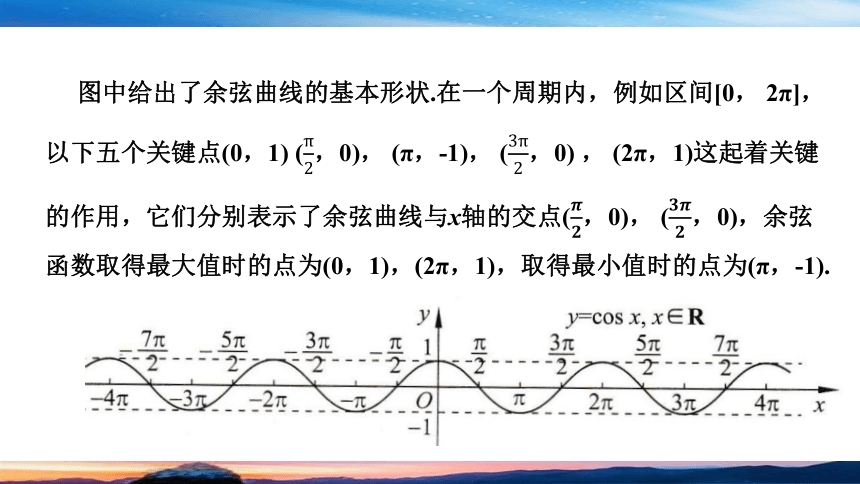
图中给出了余弦曲线的基本形状.在一个周期内,例如区间[0, 2π],以下五个关键点(0,1) (,0), (π,-1), (,0) , (2π,1)这起着关键的作用,它们分别表示了余弦曲线与x轴的交点(,0), (,0),余弦函数取得最大值时的点为(0,1),(2π,1),取得最小值时的点为(π,-1).
根据余弦曲线的基本性质,描出这五个点后,函数y=cosx在区间x∈[0,2π]的图象就基本确定了(如图).
因此,在精确度要求不太高时,常常先描出这五个关键点,然后用光滑曲线将它们顺次连接起来,就得到余弦函数的简图.这种作余弦曲线的方法也称为“五点(画图)法”.
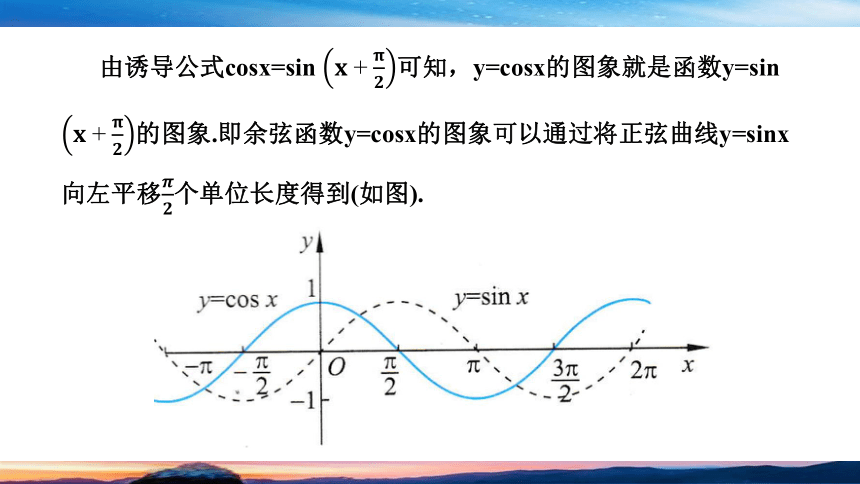
由诱导公式cosx=sin 可知,y=cosx的图象就是函数y=sin 的图象.即余弦函数y=cosx的图象可以通过将正弦曲线y=sinx向左平移个单位长度得到(如图).
例4 画出函数y=cos(x-π)在一个周期上的图象.
解 按五个关键点列表(如表).
于是得到函数y=cos(x-π)在区间[π,3π]上的五个关键点为
(π,1),(,0), (2π,-1) ,(,0), (3π,1).
描点,并用光滑曲线将它们顺次连接起来,就画出函数y=cos(x-π)在一个周期上的图象(如图).
例4 画出函数y=cos(x-π)在一个周期上的图象.
解 也可以利用诱导公式y=cos(x-π) =cosx,画出y=cosx的图象.
思考交流
画出下列函数在区间上的图象:
(1)y=2+cosx; (2) y=3cosx.
类比对正弦函数性质再认识的学习方式,通过观察图得到余弦函数y=cos x在x∈R上的主要性质.
探究点2 余弦函数性质的再认识
1.定义域
余弦函数的定义域是R.
2.周期性
由于余弦函数y=cos x的图象是由正弦曲线y=sinx向左平移个单位长度得到的.可以证明,余弦函数是周期函数,它的最小正周期是2π.
因此,为了研究问题方便,通常选取区间[0,2π]讨论其性质,然后延拓到它的定义域R上.
3.单调性
由图看到,当x由-π增大到0时,cosx的值由-1增大到1;当x由0增大到π时,cosx的值由1减小到-1.因此,余弦函数在区间[-π ,0]上单调递增,在区间[0, π]上单调递减.由余弦函数的周期性可知,余弦函数在区间[(2k-1)π,2kπ] ,k∈Z上都单调递增,在每一个区间[2kπ,(2k+1)π] , k∈Z上都单调递减.
当x= 2kπ,k∈Z时,余弦函数取得最大值1;
当x= (2k+1)π ,k∈Z时,余弦函数取得最小值-1.
余弦函数的值域是[-1,1].
4.最大(小)值和值域
5.奇偶性
余弦曲线关于y轴对称(如图).由诱导公式cos(-x)=cosx可知,余弦函数是偶函数.
例5 画出函数y=cosx-1在一个周期上的图象,并根据图象讨论函数的性质.
解 函数y=cosx-1的最小正周期是2π,按五个关键点列表(如表).
于是得到函数y=cosx-1在区间[0,2π]的五个关键点为(0,0) ,(,-1),(π,-2),(,-1),(2π,0).
描点,并用光滑曲线将它们顺次连接起来,就画出函数y=cosx-1在区间[0,2π]上的图象,如图.
由函数y=cosx-1的图象得到它的主要性质(如表).
思考交流
请借助余弦函数y=cosx的图象,求满足不等式cosx≥的x的取值范围.
取值范围: [2kπ -, +2kπ]
A
D
-9
白发无凭吾老矣!青春不再汝知乎?年将弱冠非童子,学不成名岂丈夫?
——俞良弼
§5.2余弦函数的图象与性质再认识
图象的平移变换(a>0,b>0)
向上平移 b个单位长度
向下平移 b个单位长度
f(x)
向左平移a个单位长度
向右平移a个单位长度
f(x)-b
f(x)+b
f(x+a)
f(x-a)
图象的对称变换
f(x)
关于x轴对称
-f(x)
f(-x)
关于y轴对称
1.能正确使用“五点法”、“图象变换法”画出余弦函数的简图2.掌握余弦函数的性质,会求余弦函数的最小正周期,单调区间和最值.
1.通过画余弦函数的图象,培养直观想象素养.
2.通过余弦函数的性质的应用,培养数学运算素养.
课标要求
素养要求
在区间[0,2π]上取一系列的x值,例如0, , , ,··· , 2π列表(如表).
探究点1 余弦函数的图象
利用表中的数据,先在平面直角坐标系内描点,结合对函数y=cosx性质的了解,用光滑曲线将它们顺次连接起来,就可以得到区间[[0,2π]上y=cosx的图象(如图).
由周期性可知,函数y=cosx在区间[2kπ, 2(k+1)π],k∈Z,k≠0上与在区间[0, 2π]上的函数图象形状完全相同,只是位置不同,将函数y=cosx,x ∈[0, 2π]的图象向左、右平移(每次平移2π个单位长度),就可以得到余弦函数y=cosx,x ∈R的图象(如图).
余弦函数y=cosx,x ∈R的图象称作余弦曲线.
图中给出了余弦曲线的基本形状.在一个周期内,例如区间[0, 2π],以下五个关键点(0,1) (,0), (π,-1), (,0) , (2π,1)这起着关键的作用,它们分别表示了余弦曲线与x轴的交点(,0), (,0),余弦函数取得最大值时的点为(0,1),(2π,1),取得最小值时的点为(π,-1).
根据余弦曲线的基本性质,描出这五个点后,函数y=cosx在区间x∈[0,2π]的图象就基本确定了(如图).
因此,在精确度要求不太高时,常常先描出这五个关键点,然后用光滑曲线将它们顺次连接起来,就得到余弦函数的简图.这种作余弦曲线的方法也称为“五点(画图)法”.
由诱导公式cosx=sin 可知,y=cosx的图象就是函数y=sin 的图象.即余弦函数y=cosx的图象可以通过将正弦曲线y=sinx向左平移个单位长度得到(如图).
例4 画出函数y=cos(x-π)在一个周期上的图象.
解 按五个关键点列表(如表).
于是得到函数y=cos(x-π)在区间[π,3π]上的五个关键点为
(π,1),(,0), (2π,-1) ,(,0), (3π,1).
描点,并用光滑曲线将它们顺次连接起来,就画出函数y=cos(x-π)在一个周期上的图象(如图).
例4 画出函数y=cos(x-π)在一个周期上的图象.
解 也可以利用诱导公式y=cos(x-π) =cosx,画出y=cosx的图象.
思考交流
画出下列函数在区间上的图象:
(1)y=2+cosx; (2) y=3cosx.
类比对正弦函数性质再认识的学习方式,通过观察图得到余弦函数y=cos x在x∈R上的主要性质.
探究点2 余弦函数性质的再认识
1.定义域
余弦函数的定义域是R.
2.周期性
由于余弦函数y=cos x的图象是由正弦曲线y=sinx向左平移个单位长度得到的.可以证明,余弦函数是周期函数,它的最小正周期是2π.
因此,为了研究问题方便,通常选取区间[0,2π]讨论其性质,然后延拓到它的定义域R上.
3.单调性
由图看到,当x由-π增大到0时,cosx的值由-1增大到1;当x由0增大到π时,cosx的值由1减小到-1.因此,余弦函数在区间[-π ,0]上单调递增,在区间[0, π]上单调递减.由余弦函数的周期性可知,余弦函数在区间[(2k-1)π,2kπ] ,k∈Z上都单调递增,在每一个区间[2kπ,(2k+1)π] , k∈Z上都单调递减.
当x= 2kπ,k∈Z时,余弦函数取得最大值1;
当x= (2k+1)π ,k∈Z时,余弦函数取得最小值-1.
余弦函数的值域是[-1,1].
4.最大(小)值和值域
5.奇偶性
余弦曲线关于y轴对称(如图).由诱导公式cos(-x)=cosx可知,余弦函数是偶函数.
例5 画出函数y=cosx-1在一个周期上的图象,并根据图象讨论函数的性质.
解 函数y=cosx-1的最小正周期是2π,按五个关键点列表(如表).
于是得到函数y=cosx-1在区间[0,2π]的五个关键点为(0,0) ,(,-1),(π,-2),(,-1),(2π,0).
描点,并用光滑曲线将它们顺次连接起来,就画出函数y=cosx-1在区间[0,2π]上的图象,如图.
由函数y=cosx-1的图象得到它的主要性质(如表).
思考交流
请借助余弦函数y=cosx的图象,求满足不等式cosx≥的x的取值范围.
取值范围: [2kπ -, +2kπ]
A
D
-9
白发无凭吾老矣!青春不再汝知乎?年将弱冠非童子,学不成名岂丈夫?
——俞良弼
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
