人教版九年级数学下册26.2实际问题与反比例函数同步课时作业 (word版含解析)
文档属性
| 名称 | 人教版九年级数学下册26.2实际问题与反比例函数同步课时作业 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 255.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 20:02:15 | ||
图片预览


文档简介
26.2实际问题与反比例函数
一、单选题
1.某直角三角形的面积为3,设两直角边长分别为x,y,则y关于x的函数解析式是( )
A. B. C. D.
2.2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜鹃花开”为设计理念,塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为土石方的任务,该运输公司平均运送土石方的速度v(单位:/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )
A. B. C. D.
3.在化学课上,老师教同学们配制烧碱溶液,已知有烧碱24g,则溶液的浓度y(单位g/mL)与加水后溶液体积x(单位:mL)间的函数关系的图象大致是( )
A. B. C. D.
4.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系
B.菱形的面积为48,它的两条对角线的长y(cm)与x(cm)之间的关系
C.一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的密度之间的关系
D.压力为600N时,压强p与受力面积S之间的关系
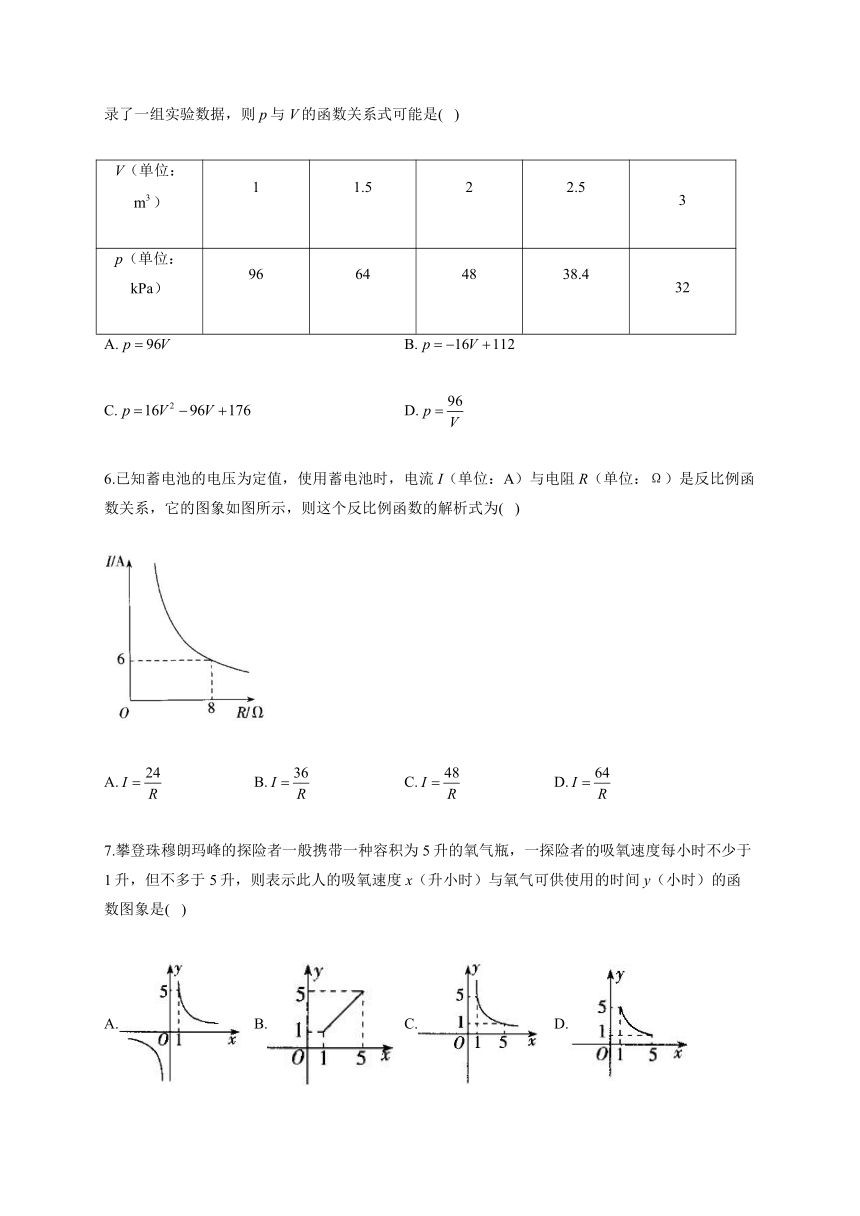
5.当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:)的函数,下表记录了一组实验数据,则p与V的函数关系式可能是( )
V(单位:) 1 1.5 2 2.5 3
p(单位:kPa) 96 64 48 38.4 32
A. B.
C. D.
6.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则这个反比例函数的解析式为( )
A. B. C. D.
7.攀登珠穆朗玛峰的探险者一般携带一种容积为5升的氧气瓶,一探险者的吸氧速度每小时不少于1升,但不多于5升,则表示此人的吸氧速度x(升小时)与氧气可供使用的时间y(小时)的函数图象是( )
A. B. C. D.
8.某药店对一种消毒液5天中的售价与销量进行调查,销量是售价的函数(统计数据见下表).已知该消毒液的进价为22元/瓶,则下列说法正确的是( )
售价x(元/瓶) 24 25 30 32 37.5
销量y(瓶) 200 192 160 150 128
A.销量是售价的正比例函数
B.每天的利润是售价的正比例函数
C.每天的利润是售价的反比例函数
D.要使每天的利润达到1600元,售价应为33元/瓶
9.在某温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积V(mL)与气体对气缸壁产生的压强p(kPa)的关系可以用如图所示的函数图象进行表示,下列说法正确的是( )
A.气压p与体积V的关系式为
B.当气压时,
C.当体积V变为原来的一半时,对应的气压p也变为原来的一半
D.当时,气压p随着体积V的增大而减小
二、填空题
10.一菱形的面积为,它的两条对角线长分别为,则a与b之间的函数关系式为__________,这个函数的图象位于第_________象限.
11.呼伦贝尔牧民斯仁达瓦家有一块牧场,放养了一群绵羊.每只绵羊啃食牧场面积y()与绵羊数x(只)之间的函数图象如图所示.又知当每只绵羊的啃食面积低于30时,会出现过度放牧的情况,造成草场退化,那么当牧场面积不变时,斯仁达瓦家最多放养绵羊_________只.
12.某段公路施行“区间限速”,一辆汽车匀速通过该段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:,其图象为如图所示的一段曲线,且端点为和,则___________,__________;若行驶速度不超过60km/h,则汽车通过该路段最少需要___________小时.
三、解答题
13.小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中水温y(℃)与开机时间x(分)成反比例关系).当水温降至20℃时,饮水机又自动开始加热,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在给饮水机通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内水的温度约为多少摄氏度.
参考答案
1.答案:D
解析:由题意可得,整理得,自变量x的取值范围是.故选D.
2.答案:A
解析:由题意,得,.故选A
3.答案:A
解析:依题意,得,即,函数图象为双曲线在第一象限的部分.故选A.
4.答案:C
解析:A项,根据速度和时间的关系式得,是反比例函数;B项,因为菱形的对角线互相垂直平分,所以,即,是反比例函数;C项,根据体积、质量m与所盛液体的密度之间的关系得,是正比例函数,不是反比例函数;D项,根据压力、压强p与受力面积S之间的关系得,是反比例函数.故选C.
5.答案:D
解析:观察发现:,故p与V的函数关系式为.
6.答案:C
解析:设,把代入,得.所以这个反比例函数的解析式为.故选C.
7.答案:D
解析:氧气瓶容积一定,则吸氧速度x与氧气可供使用的时间y成反比例函数关系,由题意知,又,所以.故选D.
8.答案:D
解析:建立平面直角坐标系,以售价为点的横坐标,销量为点的纵坐标,描点、连线可得到图象为双曲线的一支,则销量是售价的反比例函数,故A不正确;设销量与售价的函数解析式为,将,代入得,函数解析式为,设每天的利润为W元,则,该函数不是正比例函数也不是反比例函数,故B,C都不正确;当每天的利润为1600元时,,解得,即售价为33元/瓶,故D正确.故选D.
9.答案:D
解析:由物理知识知气压p与体积V成反比例关系,当时,,则,即,气压p与体积V的关系式为,故A不正确;当时,,故B不正确;当体积V变为原来的一半时,对应的气压p变为原来的2倍,故C不正确;当时,气压p随着体积V的增大而减小,故D正确.故选D.
10.答案:;一
解析:由菱形的面积公式得,故.,这个函数的图象位于第一象限.
11.答案:1500
解析:设,将代入,得,.当时,有,解得,结合题意可知最多放养1500只.
12.答案:40;80;
解析:把代入,得,则函数解析式为,再把代入,得.把代入,得,所以当行驶速度不超过60km/h时,汽车通过该路段最少需要小时.
13.答案:(1)当时,设水温y(℃)与开机时间x(分)的函数关系式为,
依据题意,得,解得,
所求函数解析式为.
(2)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为,
依据题意,得,
即,故,
当时,,解得.
(3),当时,.
答:小明散步45分钟回到家时,饮水机内水的温度约为70℃.
一、单选题
1.某直角三角形的面积为3,设两直角边长分别为x,y,则y关于x的函数解析式是( )
A. B. C. D.
2.2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜鹃花开”为设计理念,塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为土石方的任务,该运输公司平均运送土石方的速度v(单位:/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )
A. B. C. D.
3.在化学课上,老师教同学们配制烧碱溶液,已知有烧碱24g,则溶液的浓度y(单位g/mL)与加水后溶液体积x(单位:mL)间的函数关系的图象大致是( )
A. B. C. D.
4.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系
B.菱形的面积为48,它的两条对角线的长y(cm)与x(cm)之间的关系
C.一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的密度之间的关系
D.压力为600N时,压强p与受力面积S之间的关系
5.当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:)的函数,下表记录了一组实验数据,则p与V的函数关系式可能是( )
V(单位:) 1 1.5 2 2.5 3
p(单位:kPa) 96 64 48 38.4 32
A. B.
C. D.
6.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则这个反比例函数的解析式为( )
A. B. C. D.
7.攀登珠穆朗玛峰的探险者一般携带一种容积为5升的氧气瓶,一探险者的吸氧速度每小时不少于1升,但不多于5升,则表示此人的吸氧速度x(升小时)与氧气可供使用的时间y(小时)的函数图象是( )
A. B. C. D.
8.某药店对一种消毒液5天中的售价与销量进行调查,销量是售价的函数(统计数据见下表).已知该消毒液的进价为22元/瓶,则下列说法正确的是( )
售价x(元/瓶) 24 25 30 32 37.5
销量y(瓶) 200 192 160 150 128
A.销量是售价的正比例函数
B.每天的利润是售价的正比例函数
C.每天的利润是售价的反比例函数
D.要使每天的利润达到1600元,售价应为33元/瓶
9.在某温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积V(mL)与气体对气缸壁产生的压强p(kPa)的关系可以用如图所示的函数图象进行表示,下列说法正确的是( )
A.气压p与体积V的关系式为
B.当气压时,
C.当体积V变为原来的一半时,对应的气压p也变为原来的一半
D.当时,气压p随着体积V的增大而减小
二、填空题
10.一菱形的面积为,它的两条对角线长分别为,则a与b之间的函数关系式为__________,这个函数的图象位于第_________象限.
11.呼伦贝尔牧民斯仁达瓦家有一块牧场,放养了一群绵羊.每只绵羊啃食牧场面积y()与绵羊数x(只)之间的函数图象如图所示.又知当每只绵羊的啃食面积低于30时,会出现过度放牧的情况,造成草场退化,那么当牧场面积不变时,斯仁达瓦家最多放养绵羊_________只.
12.某段公路施行“区间限速”,一辆汽车匀速通过该段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:,其图象为如图所示的一段曲线,且端点为和,则___________,__________;若行驶速度不超过60km/h,则汽车通过该路段最少需要___________小时.
三、解答题
13.小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中水温y(℃)与开机时间x(分)成反比例关系).当水温降至20℃时,饮水机又自动开始加热,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在给饮水机通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内水的温度约为多少摄氏度.
参考答案
1.答案:D
解析:由题意可得,整理得,自变量x的取值范围是.故选D.
2.答案:A
解析:由题意,得,.故选A
3.答案:A
解析:依题意,得,即,函数图象为双曲线在第一象限的部分.故选A.
4.答案:C
解析:A项,根据速度和时间的关系式得,是反比例函数;B项,因为菱形的对角线互相垂直平分,所以,即,是反比例函数;C项,根据体积、质量m与所盛液体的密度之间的关系得,是正比例函数,不是反比例函数;D项,根据压力、压强p与受力面积S之间的关系得,是反比例函数.故选C.
5.答案:D
解析:观察发现:,故p与V的函数关系式为.
6.答案:C
解析:设,把代入,得.所以这个反比例函数的解析式为.故选C.
7.答案:D
解析:氧气瓶容积一定,则吸氧速度x与氧气可供使用的时间y成反比例函数关系,由题意知,又,所以.故选D.
8.答案:D
解析:建立平面直角坐标系,以售价为点的横坐标,销量为点的纵坐标,描点、连线可得到图象为双曲线的一支,则销量是售价的反比例函数,故A不正确;设销量与售价的函数解析式为,将,代入得,函数解析式为,设每天的利润为W元,则,该函数不是正比例函数也不是反比例函数,故B,C都不正确;当每天的利润为1600元时,,解得,即售价为33元/瓶,故D正确.故选D.
9.答案:D
解析:由物理知识知气压p与体积V成反比例关系,当时,,则,即,气压p与体积V的关系式为,故A不正确;当时,,故B不正确;当体积V变为原来的一半时,对应的气压p变为原来的2倍,故C不正确;当时,气压p随着体积V的增大而减小,故D正确.故选D.
10.答案:;一
解析:由菱形的面积公式得,故.,这个函数的图象位于第一象限.
11.答案:1500
解析:设,将代入,得,.当时,有,解得,结合题意可知最多放养1500只.
12.答案:40;80;
解析:把代入,得,则函数解析式为,再把代入,得.把代入,得,所以当行驶速度不超过60km/h时,汽车通过该路段最少需要小时.
13.答案:(1)当时,设水温y(℃)与开机时间x(分)的函数关系式为,
依据题意,得,解得,
所求函数解析式为.
(2)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为,
依据题意,得,
即,故,
当时,,解得.
(3),当时,.
答:小明散步45分钟回到家时,饮水机内水的温度约为70℃.
