4.4 角的比较 课件(共30张PPT)
文档属性
| 名称 | 4.4 角的比较 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 06:58:37 | ||
图片预览






文档简介
(共30张PPT)
4.4角的比较
第四章
基本平面图形
2021-2022学年七年级数学上册同步(北师版)
学习目标
1.会比较角的大小,能估计一个角的大小.
2.认识角的平分线,会画角的平分线.
3.进一步丰富对角与锐角.钝角.直角.平角.周角及它们的大小关系的认识.
导入新课
问题:有一天学生张虎和王鹏各带了一把折扇(如图),
下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角 也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
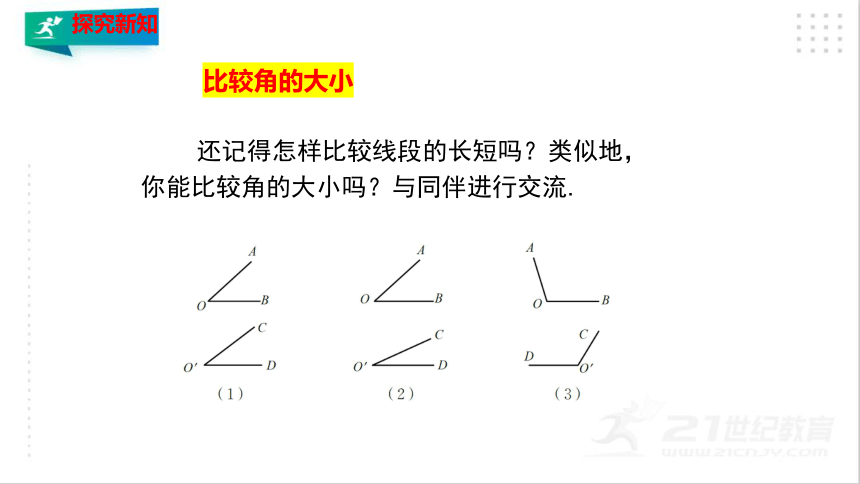
比较角的大小
还记得怎样比较线段的长短吗?类似地,你能比较角的大小吗?与同伴进行交流.
探究新知
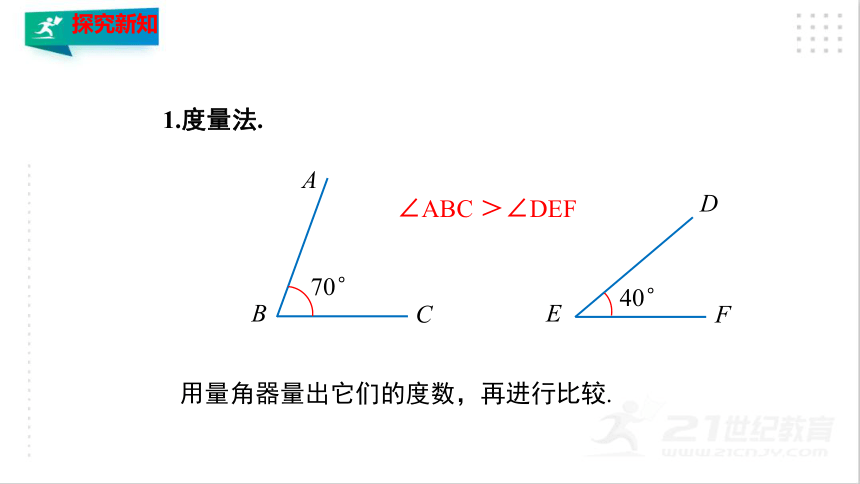
1.度量法.
B
A
C
D
E
F
70°
40°
∠ABC >∠DEF
用量角器量出它们的度数,再进行比较.
探究新知
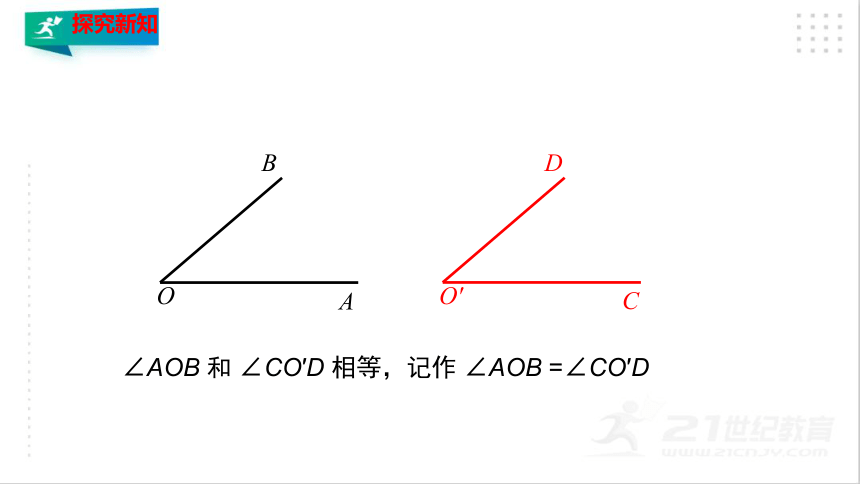
2.叠合法:
(1).将两个角的顶点及一边重合
(2).两个角的另一边落在重合一边的同侧
(3).由两个角的另一边的位置确定两个角的大小。
探究新知
O
A
B
O′
C
D
∠AOB 和 ∠CO′D 相等,记作 ∠AOB =∠CO′D
探究新知
O′
C
D
O
A
B
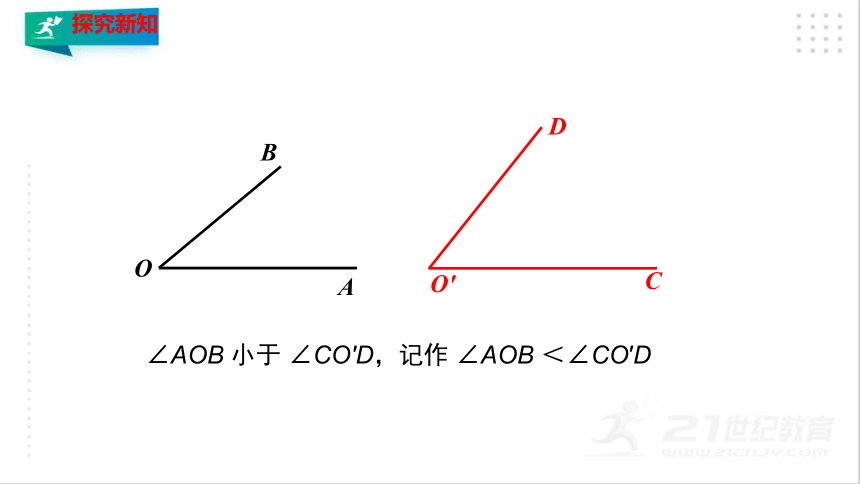
∠AOB 大于 ∠CO′D,记作 ∠AOB > ∠CO′D
探究新知
O
A
B
O′
C
D
∠AOB 小于 ∠CO′D,记作 ∠AOB <∠CO′D
探究新知
思考问题:
(1)在放大镜下,一个角的度数变大了吗?
放大镜不能放大角的度数。
探究新知
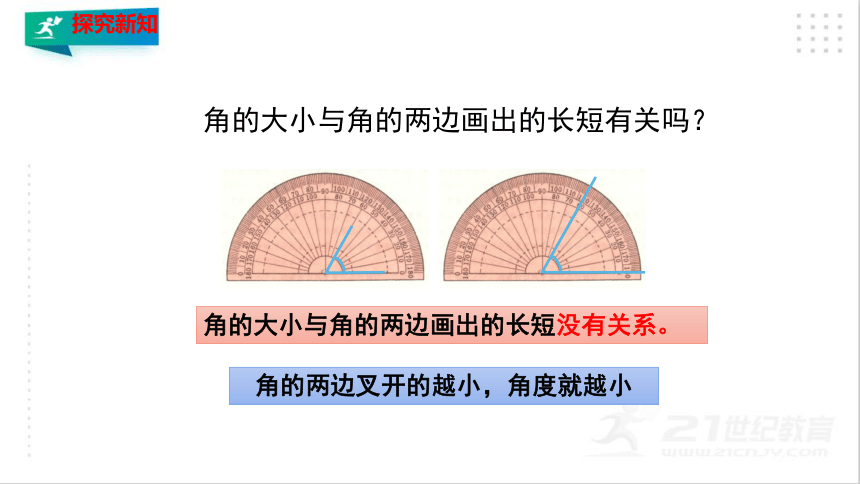
角的大小与角的两边画出的长短有关吗?
角的大小与角的两边画出的长短没有关系。
角的两边叉开的越小,角度就越小
探究新知
做一做
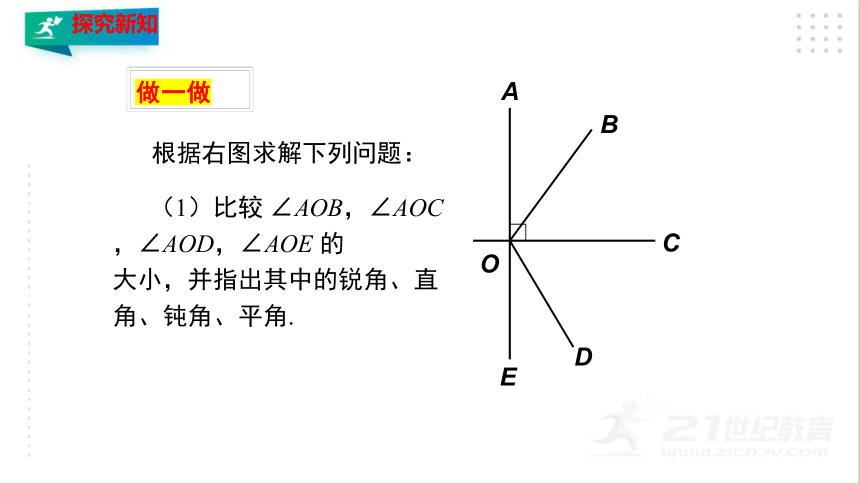
根据右图求解下列问题:
O
A
B
C
D
E
(1)比较 ∠AOB,∠AOC,∠AOD,∠AOE 的
大小,并指出其中的锐角、直角、钝角、平角.
探究新知
O
A
B
C
D
E
∠AOB<∠AOC<∠AOD<∠AOE
锐角<直角<钝角<平角
探究新知
例: 根据图,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角尺比较∠DOE与∠DOF的大小.
总结:用叠合法比较角的大小时,一定要将两个角的另一边落在重合边的同侧.两边都不重合,或有一边重合但另一边在重合边的异侧的两角,可通过度量法比较大小.
例题讲解
角平分线
活动:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?
观察思考
探究新知
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
因为OC是∠AOB的角平分线,
所以∠AOC =∠BOC = ∠AOB
或∠AOB =2∠BOC =2∠AOC
几何语言
O
B
A
C
探究新知
例题讲解
例: 如图,已知点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.
[解析] 首先应确定∠MON的转化问题:
∠MON=∠MOC+∠CON,再结合角平分线的定义,易得到∠MOC+∠CON= ∠AOB.
在有关角的计算中,几何图形与等式的性质同时使用,问题会迎刃而解.
解:因为点A,O,B在一条直线上,
所以∠AOB=180°.
因为∠AOC+∠BOC=∠AOB,
所以∠AOC+∠BOC=180°.
又因为OM,ON分别是∠AOC和∠BOC的平分线,
所以∠MOC= ∠AOC,∠CON= ∠BOC.
所以∠MOC+∠CON= (∠AOC+∠BOC)=
×180°=90°.
又因为∠MON=∠MOC+∠CON,
∴∠MON=90°.
例题讲解
课堂练习
1.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
25
2.如图,∠1=∠3,那么( ).
A.∠1=∠2 B. ∠2=∠3
C.∠AOC=∠BOD D. ∠1=
C
3.如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD等于( )
A.30° B.35°
C.20° D.40°
B
课堂练习
4. 如图,OC 是 ∠AOB 的平分线,∠BOD =
∠COD,∠BOD = 15°,则 ∠COD = _____,∠BOC = _____,∠AOB = _____.
1
3
45°
30°
60°
课堂练习
5. 已知,如图,∠AOB = 130°,∠AOD = 30°,∠BOC = 70° ,问:OC 是∠AOB 的平分线吗?OD 是∠AOC 的平分线吗?
A
D
C
B
O
解: OC不是∠AOB 的平分线
OD是∠AOC 的平分线
课堂练习
6. 如图,直线 m 外有一定点 O,A 是 m 上的一个动点,当点 A 从左向右运动时,观察∠α 和 ∠β 是如何变化的,∠α 和 ∠β 之间有关系吗?
解:∠α 越来越小,
∠β 越来越大,
∠α +∠β = 180°.
课堂练习
7. 如图(甲),∠AOC 和∠ BOD 都是直角. (1)如果∠ DOC = 28°,说出∠AOB 的度数.
∠AOD = 90°– 28°= 62°
∠AOB = 90°+ 62°= 152°
(甲)
解:
课堂练习
(2)找出图(甲)中相等的角. 如果 ∠ DOC ≠ 28°,它们还会相等吗?
(甲)
∠AOD = ∠BOC.
相等
课堂练习
(3)若 ∠DOC 变小,∠AOB 如何变化?
(甲)
∠AOB 变大.
课堂练习
8. 若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角是x°,则它的补角是(180°-x°),余角是(90°-x°) .
根据题意,得
180°-x°= 4 (90°-x°)
解得 x=60
答:这个角的度数是60 °.
课堂练习
课堂小结
角的比较
比较角的大小
角的平分线
叠合法
度量法
角的平分线的性质
角的计算
https://www.21cnjy.com/help/help_extract.php
4.4角的比较
第四章
基本平面图形
2021-2022学年七年级数学上册同步(北师版)
学习目标
1.会比较角的大小,能估计一个角的大小.
2.认识角的平分线,会画角的平分线.
3.进一步丰富对角与锐角.钝角.直角.平角.周角及它们的大小关系的认识.
导入新课
问题:有一天学生张虎和王鹏各带了一把折扇(如图),
下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角 也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
比较角的大小
还记得怎样比较线段的长短吗?类似地,你能比较角的大小吗?与同伴进行交流.
探究新知
1.度量法.
B
A
C
D
E
F
70°
40°
∠ABC >∠DEF
用量角器量出它们的度数,再进行比较.
探究新知
2.叠合法:
(1).将两个角的顶点及一边重合
(2).两个角的另一边落在重合一边的同侧
(3).由两个角的另一边的位置确定两个角的大小。
探究新知
O
A
B
O′
C
D
∠AOB 和 ∠CO′D 相等,记作 ∠AOB =∠CO′D
探究新知
O′
C
D
O
A
B
∠AOB 大于 ∠CO′D,记作 ∠AOB > ∠CO′D
探究新知
O
A
B
O′
C
D
∠AOB 小于 ∠CO′D,记作 ∠AOB <∠CO′D
探究新知
思考问题:
(1)在放大镜下,一个角的度数变大了吗?
放大镜不能放大角的度数。
探究新知
角的大小与角的两边画出的长短有关吗?
角的大小与角的两边画出的长短没有关系。
角的两边叉开的越小,角度就越小
探究新知
做一做
根据右图求解下列问题:
O
A
B
C
D
E
(1)比较 ∠AOB,∠AOC,∠AOD,∠AOE 的
大小,并指出其中的锐角、直角、钝角、平角.
探究新知
O
A
B
C
D
E
∠AOB<∠AOC<∠AOD<∠AOE
锐角<直角<钝角<平角
探究新知
例: 根据图,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角尺比较∠DOE与∠DOF的大小.
总结:用叠合法比较角的大小时,一定要将两个角的另一边落在重合边的同侧.两边都不重合,或有一边重合但另一边在重合边的异侧的两角,可通过度量法比较大小.
例题讲解
角平分线
活动:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?
观察思考
探究新知
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线的定义
因为OC是∠AOB的角平分线,
所以∠AOC =∠BOC = ∠AOB
或∠AOB =2∠BOC =2∠AOC
几何语言
O
B
A
C
探究新知
例题讲解
例: 如图,已知点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.
[解析] 首先应确定∠MON的转化问题:
∠MON=∠MOC+∠CON,再结合角平分线的定义,易得到∠MOC+∠CON= ∠AOB.
在有关角的计算中,几何图形与等式的性质同时使用,问题会迎刃而解.
解:因为点A,O,B在一条直线上,
所以∠AOB=180°.
因为∠AOC+∠BOC=∠AOB,
所以∠AOC+∠BOC=180°.
又因为OM,ON分别是∠AOC和∠BOC的平分线,
所以∠MOC= ∠AOC,∠CON= ∠BOC.
所以∠MOC+∠CON= (∠AOC+∠BOC)=
×180°=90°.
又因为∠MON=∠MOC+∠CON,
∴∠MON=90°.
例题讲解
课堂练习
1.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
25
2.如图,∠1=∠3,那么( ).
A.∠1=∠2 B. ∠2=∠3
C.∠AOC=∠BOD D. ∠1=
C
3.如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD等于( )
A.30° B.35°
C.20° D.40°
B
课堂练习
4. 如图,OC 是 ∠AOB 的平分线,∠BOD =
∠COD,∠BOD = 15°,则 ∠COD = _____,∠BOC = _____,∠AOB = _____.
1
3
45°
30°
60°
课堂练习
5. 已知,如图,∠AOB = 130°,∠AOD = 30°,∠BOC = 70° ,问:OC 是∠AOB 的平分线吗?OD 是∠AOC 的平分线吗?
A
D
C
B
O
解: OC不是∠AOB 的平分线
OD是∠AOC 的平分线
课堂练习
6. 如图,直线 m 外有一定点 O,A 是 m 上的一个动点,当点 A 从左向右运动时,观察∠α 和 ∠β 是如何变化的,∠α 和 ∠β 之间有关系吗?
解:∠α 越来越小,
∠β 越来越大,
∠α +∠β = 180°.
课堂练习
7. 如图(甲),∠AOC 和∠ BOD 都是直角. (1)如果∠ DOC = 28°,说出∠AOB 的度数.
∠AOD = 90°– 28°= 62°
∠AOB = 90°+ 62°= 152°
(甲)
解:
课堂练习
(2)找出图(甲)中相等的角. 如果 ∠ DOC ≠ 28°,它们还会相等吗?
(甲)
∠AOD = ∠BOC.
相等
课堂练习
(3)若 ∠DOC 变小,∠AOB 如何变化?
(甲)
∠AOB 变大.
课堂练习
8. 若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角是x°,则它的补角是(180°-x°),余角是(90°-x°) .
根据题意,得
180°-x°= 4 (90°-x°)
解得 x=60
答:这个角的度数是60 °.
课堂练习
课堂小结
角的比较
比较角的大小
角的平分线
叠合法
度量法
角的平分线的性质
角的计算
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
