1.5.1有理数的乘方(第一课时) 课件(共19张PPT)
文档属性
| 名称 | 1.5.1有理数的乘方(第一课时) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 888.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 15:43:19 | ||
图片预览






文档简介
(共19张PPT)
有理数的乘方(一)
复习回顾
乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
做一做:
30
0
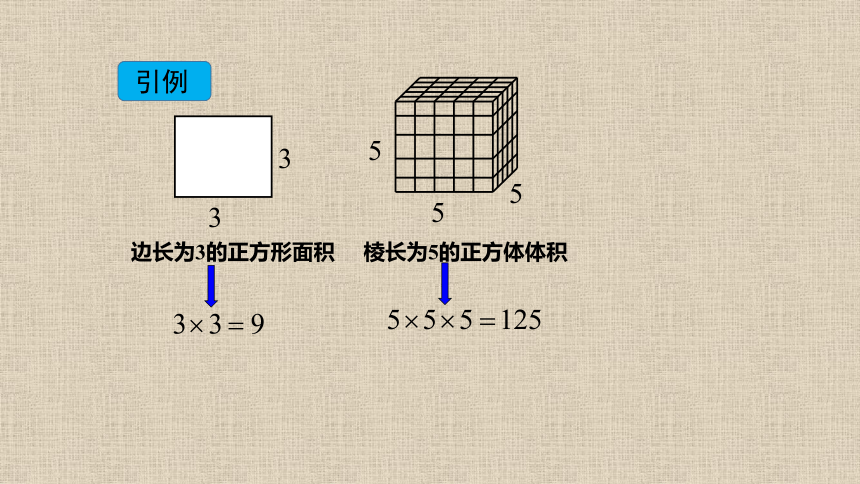
引例
3
3
5
5
5
边长为3的正方形面积
棱长为5的正方体体积
读作: 3的平方
读作: 5的立方
(或5的三次方)
记作:
记作:
引例
记作:
“-2的四次方”
记作:
“ 的五次方”
引例
读作:
读作:
记作:
“3的n次方”
记作:
引例
读作:
读作:“ a的n次方”
n个相同因数的积的运算
引例
引例
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
底数
指数
幂
剖析概念
乘方定义理解时需要关注:
1.指数n取正整数.
2.底数a可以代表所有数,可以是正数,负数,零.
3.一个数可以看作这个数本身的一次方,
例如5就是 ,指数1通常省略不写.
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
底数
指数
幂
剖析概念
乘方书写时需要关注:
1.负数的乘方,一定要把整个负数(连同负号)
用小括号括起来;
2.分数的乘方,一定要把整个分数用小括号括
起来;
(1)在 中,底数是 ,指数是 ,
读作“ ”.
9的4次方
9
4
(2)在 中,底数是 ,指数是 ,
读作“ ”.
-1
5
-1的5次方
例1.填空:
例题
(3)在 中,底数是 ,指数是 .
(4)在 中,底数是 ,指数是 .
4
6
例1.填空:
例题
-
例2.计算:
(1)
(2)
(3)
解:(1)
-
64
(2)
16
(3)
例题
(4)
(5)
(5)
(4)
-81
例题
例2.计算:
解:
想一想
与 一样吗?为什么?
-81
例3.
C .
D.
A.
B.
C
( )
例题
解析:
底数
指数
幂
课堂小结
1.有理数的乘方定义
2. 思想方法 特殊到一般
思考
珠穆朗玛峰是世界的最高峰,今年5月27日珠峰高程测量登山队登顶成功,重测它的海拔高度. 这是我们作为中国人的骄傲,有人说把一张足够大的厚度为0.1毫米的纸,连续对折27次的厚度就能超过珠穆朗玛峰. 这是真的吗?
?
珠穆朗玛峰是世界的最高峰,今年5月27日珠峰高程测量登山队登顶成功,重测它的海拔高度. 这是我们作为中国人的骄傲,有人说把一张足够大的厚度为0.1毫米的纸,连续对折27次的厚度就能超过珠穆朗玛峰. 这是真的吗?
对折 次数 1次 2次 3次 4次 ... 27次
纸的 层数 ...
层数可 表示为 ...
2
2
4
8
16
134217728
分析:
对折 次数 1次 2次 3次 4次 ... 27次
纸的 层数 ...
层数可 表示为 ...
2
2
4
8
16
2005年测量高度为8844.43米
134217728
134217728×0.1mm=13421.7728m≈13 422m
有理数的乘方(一)
复习回顾
乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,都得0.
做一做:
30
0
引例
3
3
5
5
5
边长为3的正方形面积
棱长为5的正方体体积
读作: 3的平方
读作: 5的立方
(或5的三次方)
记作:
记作:
引例
记作:
“-2的四次方”
记作:
“ 的五次方”
引例
读作:
读作:
记作:
“3的n次方”
记作:
引例
读作:
读作:“ a的n次方”
n个相同因数的积的运算
引例
引例
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
底数
指数
幂
剖析概念
乘方定义理解时需要关注:
1.指数n取正整数.
2.底数a可以代表所有数,可以是正数,负数,零.
3.一个数可以看作这个数本身的一次方,
例如5就是 ,指数1通常省略不写.
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.
底数
指数
幂
剖析概念
乘方书写时需要关注:
1.负数的乘方,一定要把整个负数(连同负号)
用小括号括起来;
2.分数的乘方,一定要把整个分数用小括号括
起来;
(1)在 中,底数是 ,指数是 ,
读作“ ”.
9的4次方
9
4
(2)在 中,底数是 ,指数是 ,
读作“ ”.
-1
5
-1的5次方
例1.填空:
例题
(3)在 中,底数是 ,指数是 .
(4)在 中,底数是 ,指数是 .
4
6
例1.填空:
例题
-
例2.计算:
(1)
(2)
(3)
解:(1)
-
64
(2)
16
(3)
例题
(4)
(5)
(5)
(4)
-81
例题
例2.计算:
解:
想一想
与 一样吗?为什么?
-81
例3.
C .
D.
A.
B.
C
( )
例题
解析:
底数
指数
幂
课堂小结
1.有理数的乘方定义
2. 思想方法 特殊到一般
思考
珠穆朗玛峰是世界的最高峰,今年5月27日珠峰高程测量登山队登顶成功,重测它的海拔高度. 这是我们作为中国人的骄傲,有人说把一张足够大的厚度为0.1毫米的纸,连续对折27次的厚度就能超过珠穆朗玛峰. 这是真的吗?
?
珠穆朗玛峰是世界的最高峰,今年5月27日珠峰高程测量登山队登顶成功,重测它的海拔高度. 这是我们作为中国人的骄傲,有人说把一张足够大的厚度为0.1毫米的纸,连续对折27次的厚度就能超过珠穆朗玛峰. 这是真的吗?
对折 次数 1次 2次 3次 4次 ... 27次
纸的 层数 ...
层数可 表示为 ...
2
2
4
8
16
134217728
分析:
对折 次数 1次 2次 3次 4次 ... 27次
纸的 层数 ...
层数可 表示为 ...
2
2
4
8
16
2005年测量高度为8844.43米
134217728
134217728×0.1mm=13421.7728m≈13 422m
