青岛版九年级上册1.6中位线定理(2)
文档属性
| 名称 | 青岛版九年级上册1.6中位线定理(2) |  | |
| 格式 | zip | ||
| 文件大小 | 241.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-19 16:05:55 | ||
图片预览



文档简介
(共14张PPT)
九年级数学(上)第一章:特殊四边形
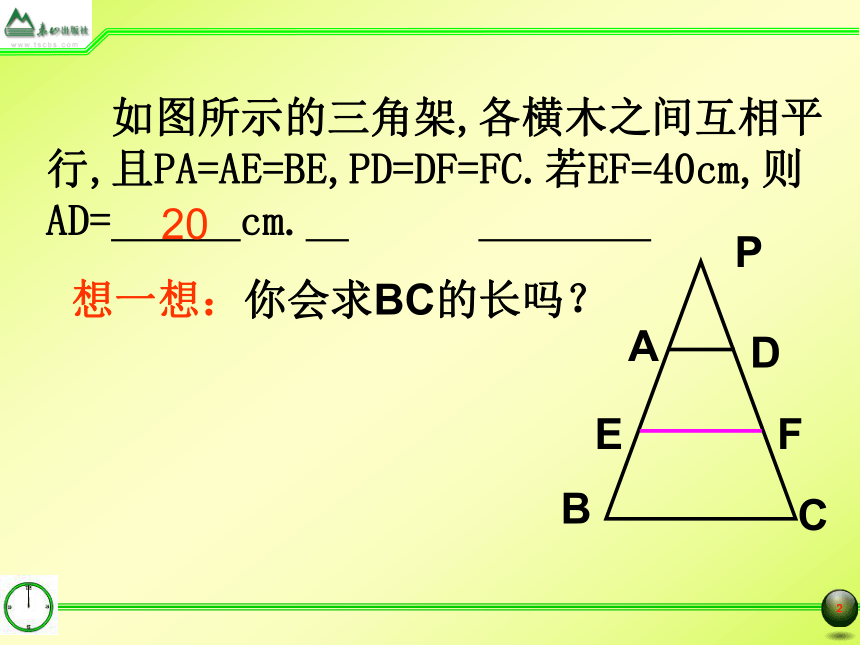
如图所示的三角架,各横木之间互相平
行,且PA=AE=BE,PD=DF=FC.若EF=40cm,则
AD= cm.
想一想:你会求BC的长吗?
P
A
E
B
C
D
F
20
学习目标:
1.理解并掌握梯形中位线的概念和梯形中位线定理;
2.能够应用梯形中位线概念及定理进行有关的论证和计算,进一步提高学生的计算能力和分析能力。
重点、难点:
梯形中位线定理的证明及应用。
阅读课本第36页至38页,完成以下内容:
1、什么叫梯形的中位线?
2、梯形中位线定理是什么?
3、如何证明梯形中位线定理?
自主学习
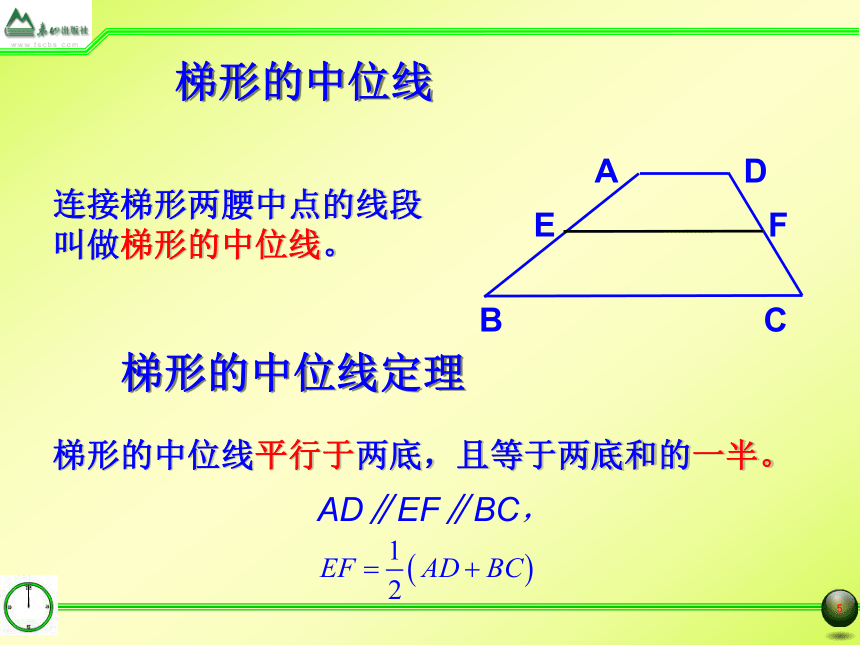
梯形的中位线
A
B
C
D
连接梯形两腰中点的线段叫做梯形的中位线。
E
F
梯形的中位线定理
梯形的中位线平行于两底,且等于两底和的一半。
AD∥EF∥BC,
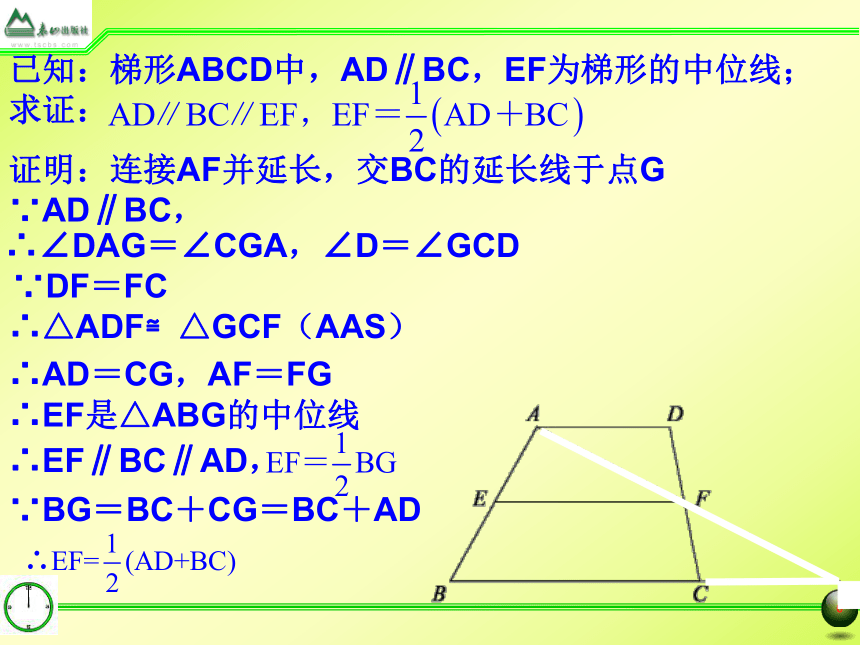
已知:梯形ABCD中,AD∥BC,EF为梯形的中位线;
求证:
证明:连接AF并延长,交BC的延长线于点G
∵AD∥BC,
∴∠DAG=∠CGA,∠D=∠GCD
∵DF=FC
∴△ADF≌△GCF(AAS)
∴AD=CG,AF=FG
∴EF是△ABG的中位线
∴EF∥BC∥AD,
∵BG=BC+CG=BC+AD
例2 等腰梯形的一个角为45°,高为h,中位线是m,求梯形的上底长
A
B
M
C
E
F
D
45°
解:如图,在梯形ABCD中,AD ∥ BC,AB=CD,∠B=45 ,E,F分别是腰AB与CD的中点,EF=m,AM⊥BC垂足为M,AM=h,作DN⊥BC,垂足为N
A
B
M
C
D
E
F
如果例2中的梯形是一个任意梯形,你能用m与h表示出梯形的面积吗?
梯形的面积公式
∵S= (AD+BC) AG
EF= (AD+BC)
∴ S=EF AG
梯形的面积等于中位线与高的乘积
∴ S=m·h
达标测试
1. (1)梯形的上底长4cm,下底长6cm,则中位线长 cm.
(2)梯形上底长6cm,中位线长8cm,则下底长 cm.
(3)等腰梯形的中位线长6cm,腰长5cm,则梯形的周长是 cm.
5
10
22
6
5
5
(4)若梯形的中位线长6cm,高为5cm,你会求梯形的面积吗?
(5)一个等腰梯形的周长80cm,如果中位线长与腰长相等,高为12cm,求梯形的面积.
30c㎡
240c㎡
2.如图,在直角梯形ABCD中,点M为CD
的中点.
(1)测量顶点A、B到点M的距离,你有什么
发现?
(2)你的结论正确吗?说明理由.
·
M
A
B
C
D
·
E
作业
九年级数学(上)第一章:特殊四边形
如图所示的三角架,各横木之间互相平
行,且PA=AE=BE,PD=DF=FC.若EF=40cm,则
AD= cm.
想一想:你会求BC的长吗?
P
A
E
B
C
D
F
20
学习目标:
1.理解并掌握梯形中位线的概念和梯形中位线定理;
2.能够应用梯形中位线概念及定理进行有关的论证和计算,进一步提高学生的计算能力和分析能力。
重点、难点:
梯形中位线定理的证明及应用。
阅读课本第36页至38页,完成以下内容:
1、什么叫梯形的中位线?
2、梯形中位线定理是什么?
3、如何证明梯形中位线定理?
自主学习
梯形的中位线
A
B
C
D
连接梯形两腰中点的线段叫做梯形的中位线。
E
F
梯形的中位线定理
梯形的中位线平行于两底,且等于两底和的一半。
AD∥EF∥BC,
已知:梯形ABCD中,AD∥BC,EF为梯形的中位线;
求证:
证明:连接AF并延长,交BC的延长线于点G
∵AD∥BC,
∴∠DAG=∠CGA,∠D=∠GCD
∵DF=FC
∴△ADF≌△GCF(AAS)
∴AD=CG,AF=FG
∴EF是△ABG的中位线
∴EF∥BC∥AD,
∵BG=BC+CG=BC+AD
例2 等腰梯形的一个角为45°,高为h,中位线是m,求梯形的上底长
A
B
M
C
E
F
D
45°
解:如图,在梯形ABCD中,AD ∥ BC,AB=CD,∠B=45 ,E,F分别是腰AB与CD的中点,EF=m,AM⊥BC垂足为M,AM=h,作DN⊥BC,垂足为N
A
B
M
C
D
E
F
如果例2中的梯形是一个任意梯形,你能用m与h表示出梯形的面积吗?
梯形的面积公式
∵S= (AD+BC) AG
EF= (AD+BC)
∴ S=EF AG
梯形的面积等于中位线与高的乘积
∴ S=m·h
达标测试
1. (1)梯形的上底长4cm,下底长6cm,则中位线长 cm.
(2)梯形上底长6cm,中位线长8cm,则下底长 cm.
(3)等腰梯形的中位线长6cm,腰长5cm,则梯形的周长是 cm.
5
10
22
6
5
5
(4)若梯形的中位线长6cm,高为5cm,你会求梯形的面积吗?
(5)一个等腰梯形的周长80cm,如果中位线长与腰长相等,高为12cm,求梯形的面积.
30c㎡
240c㎡
2.如图,在直角梯形ABCD中,点M为CD
的中点.
(1)测量顶点A、B到点M的距离,你有什么
发现?
(2)你的结论正确吗?说明理由.
·
M
A
B
C
D
·
E
作业
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
