2021-2022学年 人教版数学三年级下册4.2.4 用连除或乘除混合运算解决实际问题 课件 (共21张PPT)
文档属性
| 名称 | 2021-2022学年 人教版数学三年级下册4.2.4 用连除或乘除混合运算解决实际问题 课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 20:30:05 | ||
图片预览





文档简介
(共21张PPT)
人教版数学三年级(下)
第4课时 用连除或乘除混合运算解决
实际问题
两位数乘两位数
4
2.笔算乘法
1.经历运用连除或乘除混合运算解决实际问题的过程,能够列出综合算式。
2.经历从实际生活中发现问题、提出问题、解决问题的过程,能所学的知识运用到实际生活中。
3.感受数学的魅力,增强学习数学的兴趣,进一步培养应用意识。
学习目标
【重点】
能用连除或乘除混合运算正确解答问题,能列出综
合算式。
【难点】
获得用连除或乘除混合运算解决实际
问题的活动经验,培养应用意识。
探究新知
4
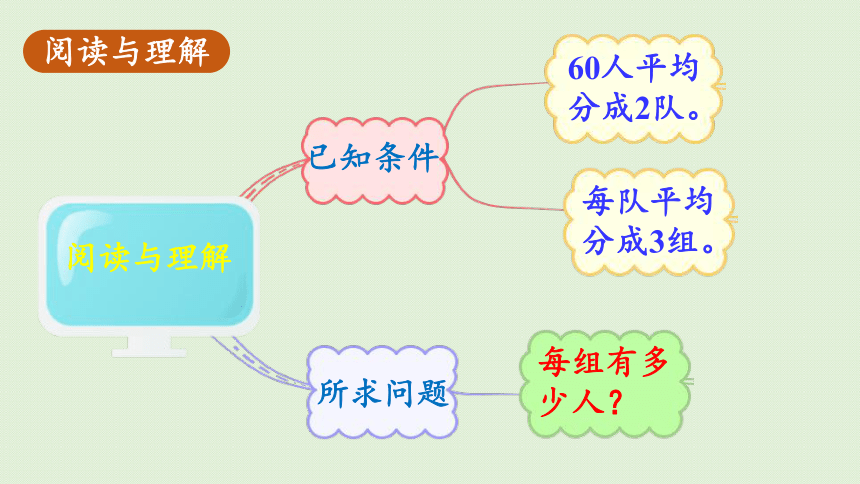
三年级女生要进行集体舞表演。老师将参加表演的60人平均分成2队,每队平均分成3组。每组有多少人?
你知道了哪些数学信息?
?
(教材第53页例4)
阅读与理解
所求问题
60人平均分成2队。
每队平均分成3组。
已知条件
阅读与理解
每组有多少人?
总人数
平均分成的队数
÷
每队人数
每队平均分成的组数
每组人数
÷
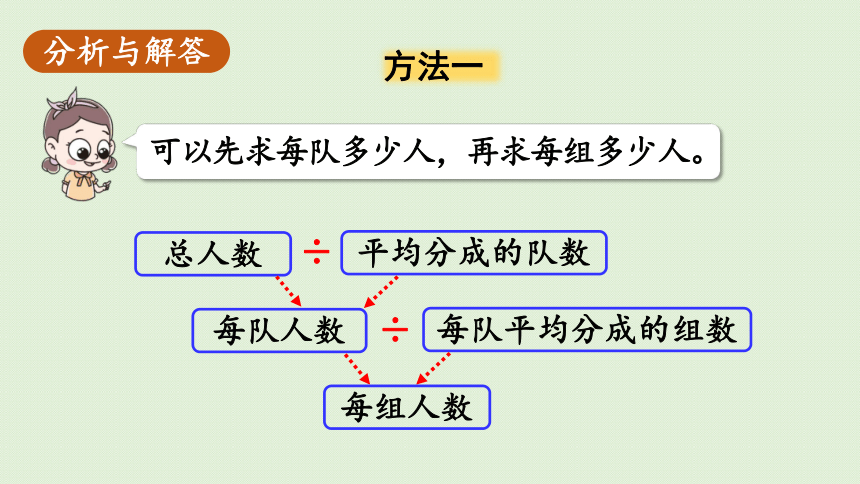
分析与解答
方法一
可以先求每队多少人,再求每组多少人。
60÷2=30(人)
(1)每队多少人?
60÷2÷3
=30÷3
=10(人)
30÷3=10(人)
(2)每组多少人?
方法一
综合算式
分步算式
总人数
每队平均分成的组数
×
一共分成的组数
2队
每组人数
÷
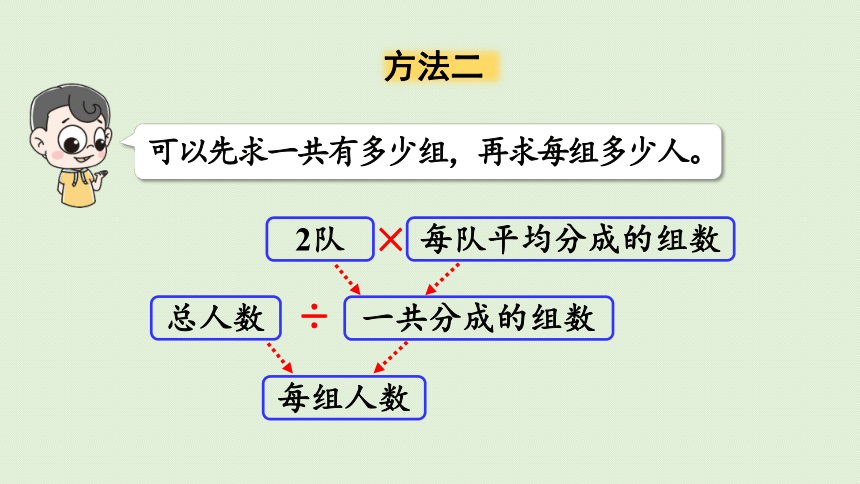
方法二
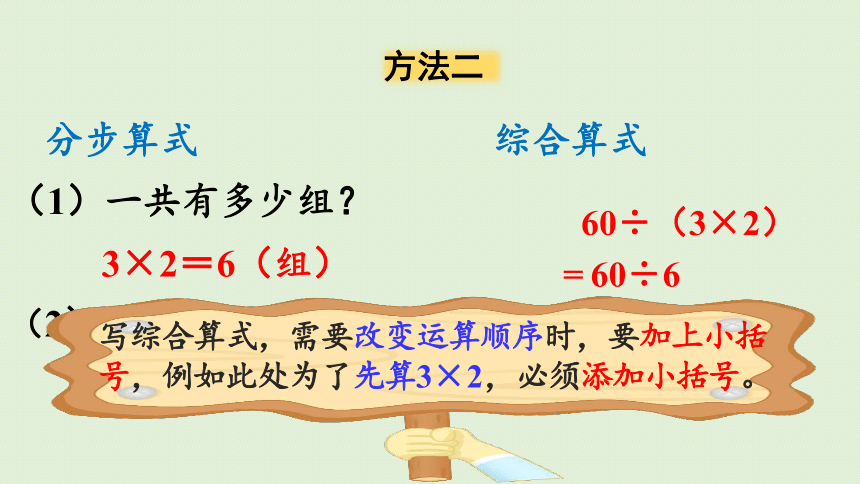
可以先求一共有多少组,再求每组多少人。
3×2=6(组)
(1)一共有多少组?
60÷(3×2)
=60÷6
=10(人)
60÷6=10(人)
(2)每组多少人?
答:每组有10人。
方法二
综合算式
分步算式
写综合算式,需要改变运算顺序时,要加上小括号,例如此处为了先算3×2,必须添加小括号。
能列式成“60÷3÷2”吗?为什么?
想一想:
总人数和每队分成的组数没有对应的数量关系,所以不能用60÷3。
再求每组有多少人
1
先求每队有多少人
2
先求一共有多少组
再求每组有多少人
解决同一问题可以有多种策略,思考的角度不同,解题的方法也不同。
回顾与反思
10×3×2
=30×2
=60(人)
检验方法的合理性
方法二
方法一
每队人数×队数=总人数
组数×每组人数=总人数
3×2×10
=6×10
=60(人)
结
果
一
致
方
法
正
确
结果一致
方法正确
课堂练习
教材第53页“做一做”
做一做
1.有一种杯子,6个杯子装一盒,8盒装一箱。960个杯子可以装多少箱?
答:960个杯子可以装20箱。
可以先求能装多少盒,再求能装多少箱。
960÷6÷8
=160÷8
=20(箱)
答:960个杯子可以装20箱。
可以先求一箱能装多少个,再求能装多少箱。
960÷(8×6)
=960÷48
=20(箱)
做一做
1.有一种杯子,6个杯子装一盒,8盒装一箱。960个杯子可以装多少箱?
2.先计算,再列出综合算式。
783÷3÷9=29
783÷3
÷9
261
29
÷4
912
38
228÷6
912÷4÷6=38
3.东东从图书馆借了一本300页的故事书,他计划5天看完,每天看2小时。东东计划每小时看多少页?
300÷5=60(页)
60÷2=30(页)
综合算式:
300÷5÷2
=60÷2
=30(页)
答:东东计划每小时看30页。
先求计划每天看几页
再求计划每小时看几页
方法二
方法一
4.平均每辆车每次运多少千克?
答:平均每辆车每次运1600千克。
9600÷2÷3
=4800÷3
=1600(千克)
9600÷(2×3)
=9600÷6
=1600(千克)
方法二
方法一
(教材第55页第6题)
1.用一个杯子往一个空瓶里倒水。倒进4杯水后,连瓶共重500克,倒进6杯水后,连瓶共重710克,1杯水和空瓶分别重多少克
提升练习
答:1杯水重105克,1个空瓶重80克。
500克
710克
多的水的杯数:
多的两杯水重:
6-4=2(杯)
710-500=210(克)
210÷2=105(克)
1杯水重:
4杯水重:
105×4=420(克)
空瓶重:
500-420=80(克)
解题技巧
解决这类问题,可以先借助图示分析题意,找出变化的量,分析变化的原因,然后根据所提供的信息层层深入,逐步解决问题。
这节课你有什么收获?
课堂小结
用连除或乘除混合运算解决实际问题
根据已知条件找中间量,确定先算什么,再算什么。
同一个问题,思路不同,
解决问题的方法也不同。
有小括号先算小括号,同
级运算按从左到右计算。
1
2
3
相关练习。
02
01
课后练习十二第7题。
课后作业
人教版数学三年级(下)
第4课时 用连除或乘除混合运算解决
实际问题
两位数乘两位数
4
2.笔算乘法
1.经历运用连除或乘除混合运算解决实际问题的过程,能够列出综合算式。
2.经历从实际生活中发现问题、提出问题、解决问题的过程,能所学的知识运用到实际生活中。
3.感受数学的魅力,增强学习数学的兴趣,进一步培养应用意识。
学习目标
【重点】
能用连除或乘除混合运算正确解答问题,能列出综
合算式。
【难点】
获得用连除或乘除混合运算解决实际
问题的活动经验,培养应用意识。
探究新知
4
三年级女生要进行集体舞表演。老师将参加表演的60人平均分成2队,每队平均分成3组。每组有多少人?
你知道了哪些数学信息?
?
(教材第53页例4)
阅读与理解
所求问题
60人平均分成2队。
每队平均分成3组。
已知条件
阅读与理解
每组有多少人?
总人数
平均分成的队数
÷
每队人数
每队平均分成的组数
每组人数
÷
分析与解答
方法一
可以先求每队多少人,再求每组多少人。
60÷2=30(人)
(1)每队多少人?
60÷2÷3
=30÷3
=10(人)
30÷3=10(人)
(2)每组多少人?
方法一
综合算式
分步算式
总人数
每队平均分成的组数
×
一共分成的组数
2队
每组人数
÷
方法二
可以先求一共有多少组,再求每组多少人。
3×2=6(组)
(1)一共有多少组?
60÷(3×2)
=60÷6
=10(人)
60÷6=10(人)
(2)每组多少人?
答:每组有10人。
方法二
综合算式
分步算式
写综合算式,需要改变运算顺序时,要加上小括号,例如此处为了先算3×2,必须添加小括号。
能列式成“60÷3÷2”吗?为什么?
想一想:
总人数和每队分成的组数没有对应的数量关系,所以不能用60÷3。
再求每组有多少人
1
先求每队有多少人
2
先求一共有多少组
再求每组有多少人
解决同一问题可以有多种策略,思考的角度不同,解题的方法也不同。
回顾与反思
10×3×2
=30×2
=60(人)
检验方法的合理性
方法二
方法一
每队人数×队数=总人数
组数×每组人数=总人数
3×2×10
=6×10
=60(人)
结
果
一
致
方
法
正
确
结果一致
方法正确
课堂练习
教材第53页“做一做”
做一做
1.有一种杯子,6个杯子装一盒,8盒装一箱。960个杯子可以装多少箱?
答:960个杯子可以装20箱。
可以先求能装多少盒,再求能装多少箱。
960÷6÷8
=160÷8
=20(箱)
答:960个杯子可以装20箱。
可以先求一箱能装多少个,再求能装多少箱。
960÷(8×6)
=960÷48
=20(箱)
做一做
1.有一种杯子,6个杯子装一盒,8盒装一箱。960个杯子可以装多少箱?
2.先计算,再列出综合算式。
783÷3÷9=29
783÷3
÷9
261
29
÷4
912
38
228÷6
912÷4÷6=38
3.东东从图书馆借了一本300页的故事书,他计划5天看完,每天看2小时。东东计划每小时看多少页?
300÷5=60(页)
60÷2=30(页)
综合算式:
300÷5÷2
=60÷2
=30(页)
答:东东计划每小时看30页。
先求计划每天看几页
再求计划每小时看几页
方法二
方法一
4.平均每辆车每次运多少千克?
答:平均每辆车每次运1600千克。
9600÷2÷3
=4800÷3
=1600(千克)
9600÷(2×3)
=9600÷6
=1600(千克)
方法二
方法一
(教材第55页第6题)
1.用一个杯子往一个空瓶里倒水。倒进4杯水后,连瓶共重500克,倒进6杯水后,连瓶共重710克,1杯水和空瓶分别重多少克
提升练习
答:1杯水重105克,1个空瓶重80克。
500克
710克
多的水的杯数:
多的两杯水重:
6-4=2(杯)
710-500=210(克)
210÷2=105(克)
1杯水重:
4杯水重:
105×4=420(克)
空瓶重:
500-420=80(克)
解题技巧
解决这类问题,可以先借助图示分析题意,找出变化的量,分析变化的原因,然后根据所提供的信息层层深入,逐步解决问题。
这节课你有什么收获?
课堂小结
用连除或乘除混合运算解决实际问题
根据已知条件找中间量,确定先算什么,再算什么。
同一个问题,思路不同,
解决问题的方法也不同。
有小括号先算小括号,同
级运算按从左到右计算。
1
2
3
相关练习。
02
01
课后练习十二第7题。
课后作业
