2021-2022学年人教版数学三年级下册5.3 长方形、正方形的面积计算公式 课件(共34张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学三年级下册5.3 长方形、正方形的面积计算公式 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 20:36:32 | ||
图片预览





文档简介
(共34张PPT)
人教版数学三年级(下)
第3课时 长方形、正方形的面积计算公式
面 积
5
1.掌握长方形、正方形的面积计算公式,并能解决一些简单的实际问题。
2.在活动中经历长方形、正方形面积计算公式的推导过程,培养观察、判断、推理、概括等能力。
3.认识到数学与实际生活是密切联系的,培养热爱生活、热爱数学的情感。
学习目标
【重点】
掌握长方形、正方形面积的计算方法。
【难点】
长方形、正方形面积计算公式的推导
过程。
探究新知
(1)一个长方形长5厘米、宽3厘米。你能求出它的面积吗?
4
5厘米
3厘米
如何求长方形的面积呢?
(教材第66页例4)
合作要求
1.利用手中1平方厘米的小正方体学具,摆一
摆,数一数。
2.小组内交流分享你的发现。
小组合作
1
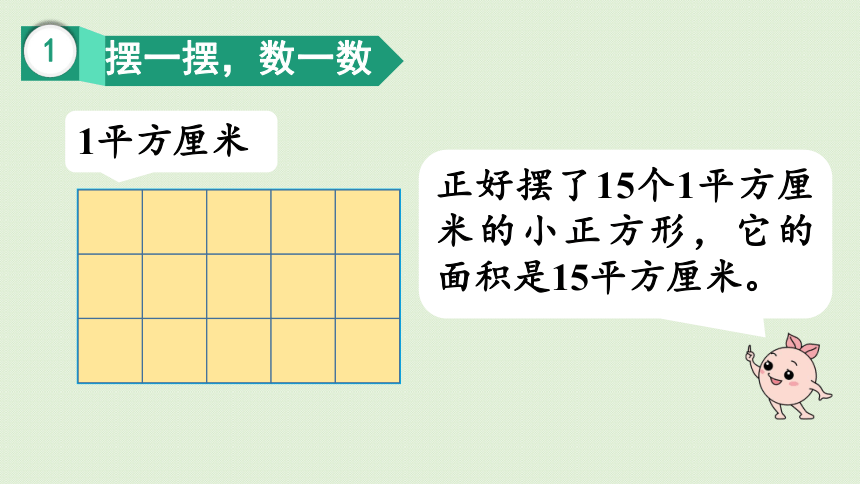
摆一摆,数一数
正好摆了15个1平方厘米的小正方形,它的面积是15平方厘米。
1平方厘米
长是5厘米,每行能摆5个小正方形。
宽是3厘米,能摆3行小正方形。
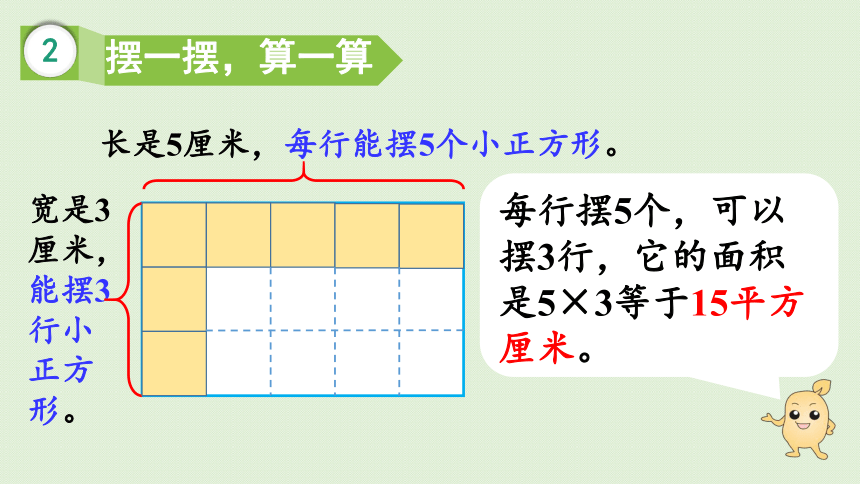
2
摆一摆,算一算
每行摆5个,可以摆3行,它的面积是5×3等于15平方厘米。
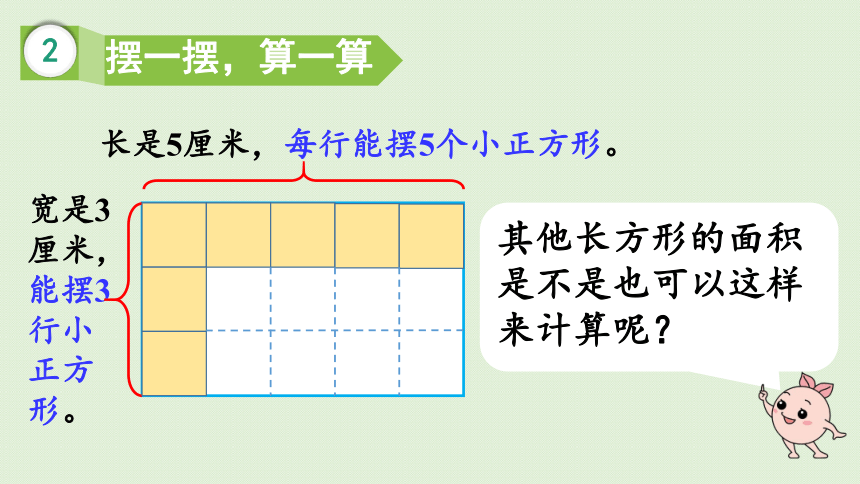
长是5厘米,每行能摆5个小正方形。
宽是3厘米,能摆3行小正方形。
2
摆一摆,算一算
其他长方形的面积是不是也可以这样来计算呢?
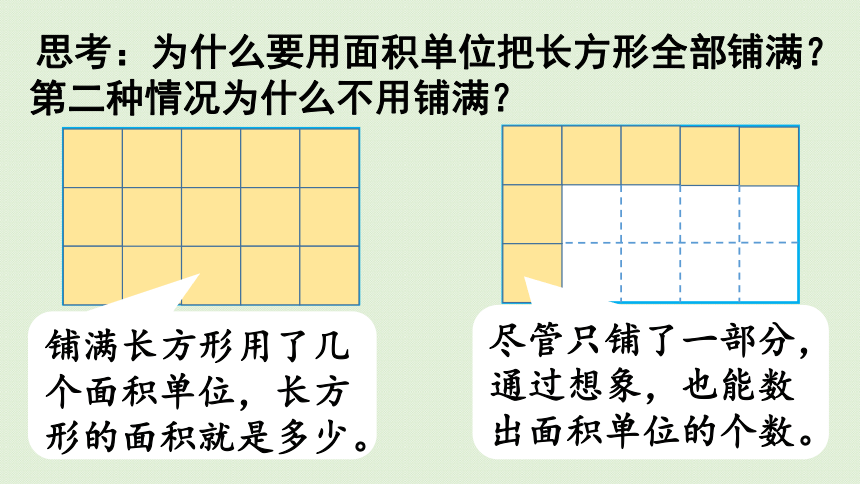
思考:为什么要用面积单位把长方形全部铺满?
第二种情况为什么不用铺满?
尽管只铺了一部分,通过想象,也能数出面积单位的个数。
铺满长方形用了几个面积单位,长方形的面积就是多少。
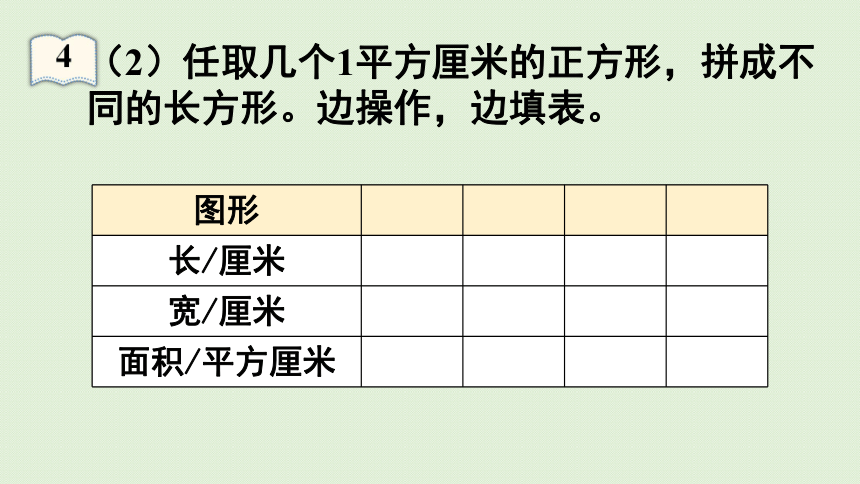
(2)任取几个1平方厘米的正方形,拼成不同的长方形。边操作,边填表。
4
图形
长/厘米
宽/厘米
面积/平方厘米
图形 ① ② ③ ④
长/厘米
宽/厘米
面积/平方厘米
①
②
③
④
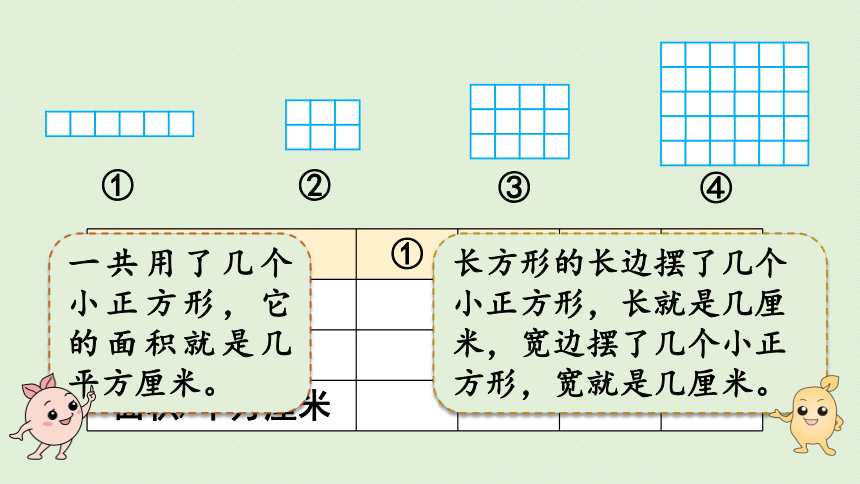
长方形的长边摆了几个小正方形,长就是几厘米,宽边摆了几个小正方形,宽就是几厘米。
一共用了几个小正方形,它的面积就是几平方厘米。
图形 ① ② ③ ④
长/厘米
宽/厘米
面积/平方厘米
①
②
③
④
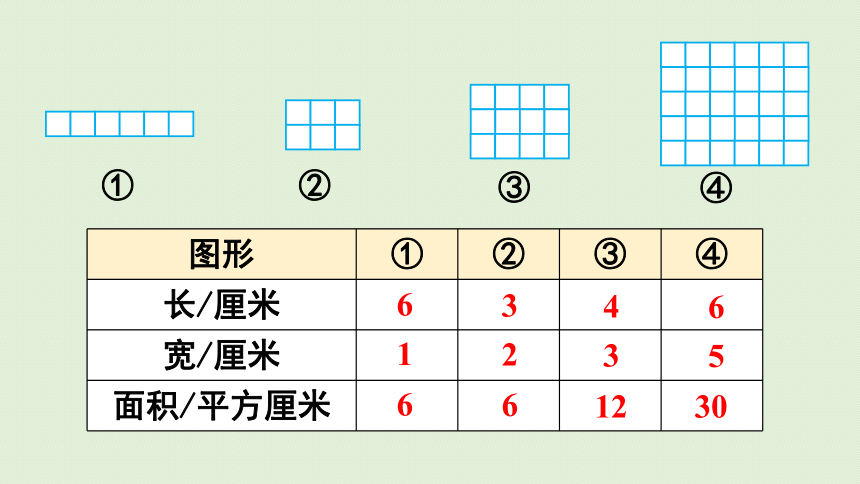
6
1
6
3
2
6
4
3
12
6
5
30
长方形的面积
长方形的长
长方形的宽
6
1
3
2
4
3
6
5
×
=
×
=
×
=
×
=
6
6
12
30
你能推导出长方形的面积计算公式吗?
分析数据:
小正方形的总数
每行的个数
行数
长方形的面积
长方形的长
长方形的宽
推导长方形的面积计算公式:
小正方形的总数
每行的个数
行数
×
=
×
=
长方形的面积=长×宽
你能灵活运用长方形面积计算公式吗?
长方形的面积
长
宽
×
=
积
×
=
长方形的宽
面积
长
÷
=
一个乘数
积
另一个乘数
÷
=
……
乘数
……
乘数
……
长方形的长
面积
宽
÷
=
(3)先量一量,再计算它们的面积。
4
长=
宽=
面积=
长=
宽=
面积=
如何求图形的面积?
测量这两个图形的长和宽,再运用长方形的面积计算公式计算。
5厘米
2厘米
3厘米
3厘米
你有什么发现?
长=
宽=
面积=
长=
宽=
面积=
5厘米
2厘米
10平方厘米
3厘米
3厘米
9平方厘米
5×2=10(平方厘米)
3×3=9(平方厘米)
第2个长方形的长和宽相等。
正方形是特殊的长方形。
长方形长和宽相等时,这个长方形就是正方形。
长方形的面积 = 长 × 宽
边长
边长
正方形的面积
×
=
长3厘米
长3厘米
课堂练习
教材第67页“做一做”
1.一张长方形的A4纸(如下图),它
做一做
30厘米
21厘米
30×21=630(平方厘米)
答:它的面积是630平方厘米。
长方形的面积=长×宽
的面积是多少平方厘米?
如果从这张纸上剪下一个最大的正方形,
做一做
30厘米
21厘米
21×21=441(平方厘米)
答:它的面积是441平方厘米。
正方形的边长等于长方形的宽。
正方形的面积=边长×边长
这个正方形的面积是多少?
2.一个长方形长3米,宽10分米,这个长方形的面积是多少平方分米?
30×10=300(平方分米)
答:这个长方形的面积是300平方分米。
3米=30分米
先统一单位再计算。
3.填空。
(1)王阿姨家的客厅长6( ),宽4( ),
面积是( )。
(2)边长1米的正方形,面积是( )。
(3)一个正方形的边长是11分米,面积是(
),周长是( )。
(4)长方形的面积是128平方米,宽是8米,长
是( )。
米
米
24平方米
1平方米
121
平方分米
44分米
16米
灵活运用周长和面积公式。
A.120米 B.240米 C.320米 D.120平方米
E.4800平方米 F.360平方米
4.选择。
有一个长方形操场,宽是40米,长是宽的3倍。长是( )。
(1)小红沿这个操场跑一圈,要跑( )。
(2)这个操场的面积是( )。
C
E
40×3=120(米)
(120+40)×2=320(米)
120×40=4800(平方米)
A
提升练习
1.求下面图形的面积。
45+30=75(平方厘米)
15厘米
10厘米
6厘米
9厘米
9-6=3厘米
15-10=5厘米
15×(9-6)=45(平方厘米)
6×(15-10)=30(平方厘米)
方法一
15厘米
10厘米
6厘米
9厘米
9-6=3厘米
45+30=75(平方厘米)
15-10=5厘米
9×(15-10)=45(平方厘米)
10×(9-6)=30(平方厘米)
1.求下面图形的面积。
方法二
15×9=135(平方厘米)
10×6=60(平方厘米)
135-60=75(平方厘米)
答:图形的面积是75平方厘米。
15厘米
10厘米
6厘米
9厘米
1.求下面图形的面积。
方法三
解决此类问题,可以先将一个复杂的不规则图形割补成几个简单的规则图形,分别计算出各个规则图形的面积,再求出它们的和或差即可。
解题技巧归纳总结
2.一个正方形,如果边长增加3厘米,面积就增加39平方厘米,求原正方形的面积。
图形①:宽3厘米,长与原正方形的边长相同。
①
3厘米
3厘米
④
③
②
图形②:宽3厘米,长与原正方形的边长相同。
①的面积=②的面积
图形③:边长为3厘米的正方形。
3×3=9(平方厘米)
①
3厘米
3厘米
④
③
②
①的面积+②的面积=增加的面积-③的面积
39-9=30(平方厘米)
图形①的长=图形②的长
15÷3=5(厘米)
①的面积=②的面积
30÷2=15(平方厘米)
2.一个正方形,如果边长增加3厘米,面积就增加39平方厘米,求原正方形的面积。
39-3×3=30(平方厘米)
30÷2÷3=5(厘米)
5×5=25(平方厘米)
答:原正方形的面积是25平方厘米。
2.一个正方形,如果边长增加3厘米,面积就增加39平方厘米,求原正方形的面积。
①
3厘米
3厘米
④
③
②
解决此类问题,可以通过画图分析正方形边长变化后面积增加的部分与原图形的关系,从而解决问题,这种方法叫做图示法。
解题技巧归纳总结
课堂小结
长方形和正方形面积计算公式
长方形的面积=长×宽
正方形的面积=边长×边长
长方形的长=面积÷宽
长方形的宽=面积÷长
这节课你有什么收获?
相关练习。
02
01
课后练习十五第1、2题。
课后作业
人教版数学三年级(下)
第3课时 长方形、正方形的面积计算公式
面 积
5
1.掌握长方形、正方形的面积计算公式,并能解决一些简单的实际问题。
2.在活动中经历长方形、正方形面积计算公式的推导过程,培养观察、判断、推理、概括等能力。
3.认识到数学与实际生活是密切联系的,培养热爱生活、热爱数学的情感。
学习目标
【重点】
掌握长方形、正方形面积的计算方法。
【难点】
长方形、正方形面积计算公式的推导
过程。
探究新知
(1)一个长方形长5厘米、宽3厘米。你能求出它的面积吗?
4
5厘米
3厘米
如何求长方形的面积呢?
(教材第66页例4)
合作要求
1.利用手中1平方厘米的小正方体学具,摆一
摆,数一数。
2.小组内交流分享你的发现。
小组合作
1
摆一摆,数一数
正好摆了15个1平方厘米的小正方形,它的面积是15平方厘米。
1平方厘米
长是5厘米,每行能摆5个小正方形。
宽是3厘米,能摆3行小正方形。
2
摆一摆,算一算
每行摆5个,可以摆3行,它的面积是5×3等于15平方厘米。
长是5厘米,每行能摆5个小正方形。
宽是3厘米,能摆3行小正方形。
2
摆一摆,算一算
其他长方形的面积是不是也可以这样来计算呢?
思考:为什么要用面积单位把长方形全部铺满?
第二种情况为什么不用铺满?
尽管只铺了一部分,通过想象,也能数出面积单位的个数。
铺满长方形用了几个面积单位,长方形的面积就是多少。
(2)任取几个1平方厘米的正方形,拼成不同的长方形。边操作,边填表。
4
图形
长/厘米
宽/厘米
面积/平方厘米
图形 ① ② ③ ④
长/厘米
宽/厘米
面积/平方厘米
①
②
③
④
长方形的长边摆了几个小正方形,长就是几厘米,宽边摆了几个小正方形,宽就是几厘米。
一共用了几个小正方形,它的面积就是几平方厘米。
图形 ① ② ③ ④
长/厘米
宽/厘米
面积/平方厘米
①
②
③
④
6
1
6
3
2
6
4
3
12
6
5
30
长方形的面积
长方形的长
长方形的宽
6
1
3
2
4
3
6
5
×
=
×
=
×
=
×
=
6
6
12
30
你能推导出长方形的面积计算公式吗?
分析数据:
小正方形的总数
每行的个数
行数
长方形的面积
长方形的长
长方形的宽
推导长方形的面积计算公式:
小正方形的总数
每行的个数
行数
×
=
×
=
长方形的面积=长×宽
你能灵活运用长方形面积计算公式吗?
长方形的面积
长
宽
×
=
积
×
=
长方形的宽
面积
长
÷
=
一个乘数
积
另一个乘数
÷
=
……
乘数
……
乘数
……
长方形的长
面积
宽
÷
=
(3)先量一量,再计算它们的面积。
4
长=
宽=
面积=
长=
宽=
面积=
如何求图形的面积?
测量这两个图形的长和宽,再运用长方形的面积计算公式计算。
5厘米
2厘米
3厘米
3厘米
你有什么发现?
长=
宽=
面积=
长=
宽=
面积=
5厘米
2厘米
10平方厘米
3厘米
3厘米
9平方厘米
5×2=10(平方厘米)
3×3=9(平方厘米)
第2个长方形的长和宽相等。
正方形是特殊的长方形。
长方形长和宽相等时,这个长方形就是正方形。
长方形的面积 = 长 × 宽
边长
边长
正方形的面积
×
=
长3厘米
长3厘米
课堂练习
教材第67页“做一做”
1.一张长方形的A4纸(如下图),它
做一做
30厘米
21厘米
30×21=630(平方厘米)
答:它的面积是630平方厘米。
长方形的面积=长×宽
的面积是多少平方厘米?
如果从这张纸上剪下一个最大的正方形,
做一做
30厘米
21厘米
21×21=441(平方厘米)
答:它的面积是441平方厘米。
正方形的边长等于长方形的宽。
正方形的面积=边长×边长
这个正方形的面积是多少?
2.一个长方形长3米,宽10分米,这个长方形的面积是多少平方分米?
30×10=300(平方分米)
答:这个长方形的面积是300平方分米。
3米=30分米
先统一单位再计算。
3.填空。
(1)王阿姨家的客厅长6( ),宽4( ),
面积是( )。
(2)边长1米的正方形,面积是( )。
(3)一个正方形的边长是11分米,面积是(
),周长是( )。
(4)长方形的面积是128平方米,宽是8米,长
是( )。
米
米
24平方米
1平方米
121
平方分米
44分米
16米
灵活运用周长和面积公式。
A.120米 B.240米 C.320米 D.120平方米
E.4800平方米 F.360平方米
4.选择。
有一个长方形操场,宽是40米,长是宽的3倍。长是( )。
(1)小红沿这个操场跑一圈,要跑( )。
(2)这个操场的面积是( )。
C
E
40×3=120(米)
(120+40)×2=320(米)
120×40=4800(平方米)
A
提升练习
1.求下面图形的面积。
45+30=75(平方厘米)
15厘米
10厘米
6厘米
9厘米
9-6=3厘米
15-10=5厘米
15×(9-6)=45(平方厘米)
6×(15-10)=30(平方厘米)
方法一
15厘米
10厘米
6厘米
9厘米
9-6=3厘米
45+30=75(平方厘米)
15-10=5厘米
9×(15-10)=45(平方厘米)
10×(9-6)=30(平方厘米)
1.求下面图形的面积。
方法二
15×9=135(平方厘米)
10×6=60(平方厘米)
135-60=75(平方厘米)
答:图形的面积是75平方厘米。
15厘米
10厘米
6厘米
9厘米
1.求下面图形的面积。
方法三
解决此类问题,可以先将一个复杂的不规则图形割补成几个简单的规则图形,分别计算出各个规则图形的面积,再求出它们的和或差即可。
解题技巧归纳总结
2.一个正方形,如果边长增加3厘米,面积就增加39平方厘米,求原正方形的面积。
图形①:宽3厘米,长与原正方形的边长相同。
①
3厘米
3厘米
④
③
②
图形②:宽3厘米,长与原正方形的边长相同。
①的面积=②的面积
图形③:边长为3厘米的正方形。
3×3=9(平方厘米)
①
3厘米
3厘米
④
③
②
①的面积+②的面积=增加的面积-③的面积
39-9=30(平方厘米)
图形①的长=图形②的长
15÷3=5(厘米)
①的面积=②的面积
30÷2=15(平方厘米)
2.一个正方形,如果边长增加3厘米,面积就增加39平方厘米,求原正方形的面积。
39-3×3=30(平方厘米)
30÷2÷3=5(厘米)
5×5=25(平方厘米)
答:原正方形的面积是25平方厘米。
2.一个正方形,如果边长增加3厘米,面积就增加39平方厘米,求原正方形的面积。
①
3厘米
3厘米
④
③
②
解决此类问题,可以通过画图分析正方形边长变化后面积增加的部分与原图形的关系,从而解决问题,这种方法叫做图示法。
解题技巧归纳总结
课堂小结
长方形和正方形面积计算公式
长方形的面积=长×宽
正方形的面积=边长×边长
长方形的长=面积÷宽
长方形的宽=面积÷长
这节课你有什么收获?
相关练习。
02
01
课后练习十五第1、2题。
课后作业
