人教A版 选择性必修第二册 5.1 第2课时 导数的几何意义 课件(共46张PPT)
文档属性
| 名称 | 人教A版 选择性必修第二册 5.1 第2课时 导数的几何意义 课件(共46张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-13 22:12:25 | ||
图片预览







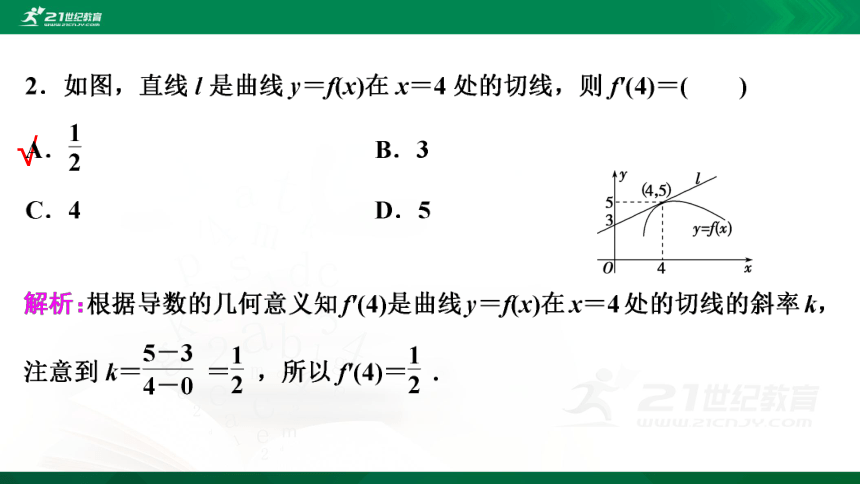




文档简介
(共46张PPT)
第五章 一元函数的导数及其应用
5.1 导数的概念及其意义
第2课时 导数的几何意义
学习指导 核心素养
1. 理解导数的几何意义并会求曲线在某点处的切线方程. 2.理解导函数的定义,会用定义法求简单函数的导函数. 1. 直观想象:导数的几何意义,曲线的切线.
2.数学运算:导数的计算.
1.导数的几何意义
(1)切线的定义
如图,在曲线y=f(x)上任取一点P(x,f(x)),如果当
点P(x,f(x)) 沿着曲线y=f(x)无限趋近于点P0(x0,
f(x0))时,割线P0P无限趋近于一个确定的位置,这
个确定位置的________称为曲线y=f(x)在点P0处的
切线.
直线P0T
f′(x0)
1.曲线的切线是否一定和曲线只有一个交点?
提示:曲线的切线并不一定与曲线只有一个交点,可以有多个,甚至可以有无穷多个.与曲线只有一个公共点的直线也不一定是曲线的切线.
2.f′(x0)和f′(x)有何关系?
提示:f′(x0)是函数y=f(x)在x=x0处的导数,是一个数值,f′(x)是一个函数;f′(x0)可看作函数f′(x)在x=x0处的函数值.
×
√
×
1.判断正误(正确的打“√”,错误的打“×”)
(1)函数在一点处的导数f′(x0)是一个常数.( )
(2)函数f(x)=0没有导数.( )
(3)“直线l与曲线C相切”是“直线l与曲线C有一个交点”的必要不充分条件.( )
√
探究点1 求切线方程
[问题探究]
什么是“以直代曲”思想?
探究感悟:用曲线上某点处的切线近似代替这一点附近的曲线,这就是“以直代曲”思想.
角度一 曲线在某点处的切线方程
已知曲线C:y=f(x)=x3+x.
(1)求曲线C在点(1,2)处切线的方程;
(2)设曲线C上任意一点处切线的倾斜角为α,求α的取值范围.
求曲线在某点处的切线方程的步骤
求曲线y=f(x)过点P(x0,y0)的切线方程的步骤
(1)设切点为A(xA,f(xA)),求切线的斜率k=f′(xA),写出切线方程(含参
数).
(2)把点P(x0,y0)的坐标代入切线方程,建立关于xA的方程,解得xA的值,进而求出切线方程.
√
探究点2 求切点坐标
过曲线y=x2上某点P的切线满足下列条件,分别求出P点.
(1)平行于直线y=4x-5;
(2)垂直于直线2x-6y+5=0;
(3)与x轴成135°的倾斜角.
求满足某条件的曲线的切点坐标的步骤
(1)先设切点坐标(x0,y0).
(2)求导函数f′(x).
(3)求切线的斜率f′(x0).
(4)由斜率间的关系列出关于x0的方程,解方程求x0.
(5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0,得切点坐标.
√
2.已知曲线f(x)=x2+6在点P处的切线平行于直线4x-y-3=0,则点P的坐标为________.
所以曲线f(x)在点P(x0,y0)处的切线的斜率为2x0.
因为切线与直线4x-y-3=0平行,
所以2x0=4,x0=2,y0=x20+6=10,
即切点坐标为(2,10).
答案:(2,10)
探究点3 利用图象理解导数的几何意义
[问题探究]
导数值的大小和曲线的升降有什么关系?
探究感悟:根据“以直代曲”思想,导数绝对值的大小反映了曲线上升或下降的快慢.
(1)已知函数f(x)的图象如图所示,则下列不等关系中正确的是( )
A.0<f′(2)<f′(3)<f(3)-f(2)
B.0<f′(2)<f(3)-f(2)<f′(3)
C.0<f′(3)<f(3)-f(2)<f′(2)
D.0<f(3)-f(2)<f′(2)<f′(3)
√
(2)(2021·甘肃会宁一中高二期末)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
√
导数与函数图象升降的关系
若函数y=f(x)在x=x0处的导数存在且f′(x0)>0(即切线的斜率大于零),则函数y=f(x)在x=x0附近的图象是上升的;若f′(x0)<0(即切线的斜率小于零),则函数y=f(x)在x=x0附近的图象是下降的.导数绝对值的大小反映了曲线上升或下降的快慢.
若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是( )
√
解析:依题意,y=f′(x)在[a,b]上是增函数,则在函数f(x)的图象上,各点的切线的斜率随着x的增大而增大,观察四个选项的图象,只有A满
足.
√
2.(多选)下面说法不正确的是( )
A.若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处没有切线
B.若曲线y=f(x)在点(x0,f(x0))处有切线,则f′(x0)必存在
C.若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处的切线斜率不存在
D.若曲线y=f(x)在点(x0,f(x0))处没有切线,则f′(x0) 有可能存在
解析:根据导数的几何意义及切线的定义知,曲线在(x0,y0)处有导数,则切线一定存在,但反之不一定成立,故A,B,D错误.
√
√
√
答案:x-y+2=0或4x-y-4=0
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第五章 一元函数的导数及其应用
5.1 导数的概念及其意义
第2课时 导数的几何意义
学习指导 核心素养
1. 理解导数的几何意义并会求曲线在某点处的切线方程. 2.理解导函数的定义,会用定义法求简单函数的导函数. 1. 直观想象:导数的几何意义,曲线的切线.
2.数学运算:导数的计算.
1.导数的几何意义
(1)切线的定义
如图,在曲线y=f(x)上任取一点P(x,f(x)),如果当
点P(x,f(x)) 沿着曲线y=f(x)无限趋近于点P0(x0,
f(x0))时,割线P0P无限趋近于一个确定的位置,这
个确定位置的________称为曲线y=f(x)在点P0处的
切线.
直线P0T
f′(x0)
1.曲线的切线是否一定和曲线只有一个交点?
提示:曲线的切线并不一定与曲线只有一个交点,可以有多个,甚至可以有无穷多个.与曲线只有一个公共点的直线也不一定是曲线的切线.
2.f′(x0)和f′(x)有何关系?
提示:f′(x0)是函数y=f(x)在x=x0处的导数,是一个数值,f′(x)是一个函数;f′(x0)可看作函数f′(x)在x=x0处的函数值.
×
√
×
1.判断正误(正确的打“√”,错误的打“×”)
(1)函数在一点处的导数f′(x0)是一个常数.( )
(2)函数f(x)=0没有导数.( )
(3)“直线l与曲线C相切”是“直线l与曲线C有一个交点”的必要不充分条件.( )
√
探究点1 求切线方程
[问题探究]
什么是“以直代曲”思想?
探究感悟:用曲线上某点处的切线近似代替这一点附近的曲线,这就是“以直代曲”思想.
角度一 曲线在某点处的切线方程
已知曲线C:y=f(x)=x3+x.
(1)求曲线C在点(1,2)处切线的方程;
(2)设曲线C上任意一点处切线的倾斜角为α,求α的取值范围.
求曲线在某点处的切线方程的步骤
求曲线y=f(x)过点P(x0,y0)的切线方程的步骤
(1)设切点为A(xA,f(xA)),求切线的斜率k=f′(xA),写出切线方程(含参
数).
(2)把点P(x0,y0)的坐标代入切线方程,建立关于xA的方程,解得xA的值,进而求出切线方程.
√
探究点2 求切点坐标
过曲线y=x2上某点P的切线满足下列条件,分别求出P点.
(1)平行于直线y=4x-5;
(2)垂直于直线2x-6y+5=0;
(3)与x轴成135°的倾斜角.
求满足某条件的曲线的切点坐标的步骤
(1)先设切点坐标(x0,y0).
(2)求导函数f′(x).
(3)求切线的斜率f′(x0).
(4)由斜率间的关系列出关于x0的方程,解方程求x0.
(5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0,得切点坐标.
√
2.已知曲线f(x)=x2+6在点P处的切线平行于直线4x-y-3=0,则点P的坐标为________.
所以曲线f(x)在点P(x0,y0)处的切线的斜率为2x0.
因为切线与直线4x-y-3=0平行,
所以2x0=4,x0=2,y0=x20+6=10,
即切点坐标为(2,10).
答案:(2,10)
探究点3 利用图象理解导数的几何意义
[问题探究]
导数值的大小和曲线的升降有什么关系?
探究感悟:根据“以直代曲”思想,导数绝对值的大小反映了曲线上升或下降的快慢.
(1)已知函数f(x)的图象如图所示,则下列不等关系中正确的是( )
A.0<f′(2)<f′(3)<f(3)-f(2)
B.0<f′(2)<f(3)-f(2)<f′(3)
C.0<f′(3)<f(3)-f(2)<f′(2)
D.0<f(3)-f(2)<f′(2)<f′(3)
√
(2)(2021·甘肃会宁一中高二期末)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
√
导数与函数图象升降的关系
若函数y=f(x)在x=x0处的导数存在且f′(x0)>0(即切线的斜率大于零),则函数y=f(x)在x=x0附近的图象是上升的;若f′(x0)<0(即切线的斜率小于零),则函数y=f(x)在x=x0附近的图象是下降的.导数绝对值的大小反映了曲线上升或下降的快慢.
若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是( )
√
解析:依题意,y=f′(x)在[a,b]上是增函数,则在函数f(x)的图象上,各点的切线的斜率随着x的增大而增大,观察四个选项的图象,只有A满
足.
√
2.(多选)下面说法不正确的是( )
A.若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处没有切线
B.若曲线y=f(x)在点(x0,f(x0))处有切线,则f′(x0)必存在
C.若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处的切线斜率不存在
D.若曲线y=f(x)在点(x0,f(x0))处没有切线,则f′(x0) 有可能存在
解析:根据导数的几何意义及切线的定义知,曲线在(x0,y0)处有导数,则切线一定存在,但反之不一定成立,故A,B,D错误.
√
√
√
答案:x-y+2=0或4x-y-4=0
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
