5解方程 奇怪的方程(课件) 人教版数学五年级上册(共14张PPT)
文档属性
| 名称 | 5解方程 奇怪的方程(课件) 人教版数学五年级上册(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 976.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
奇怪的方程
—解方程
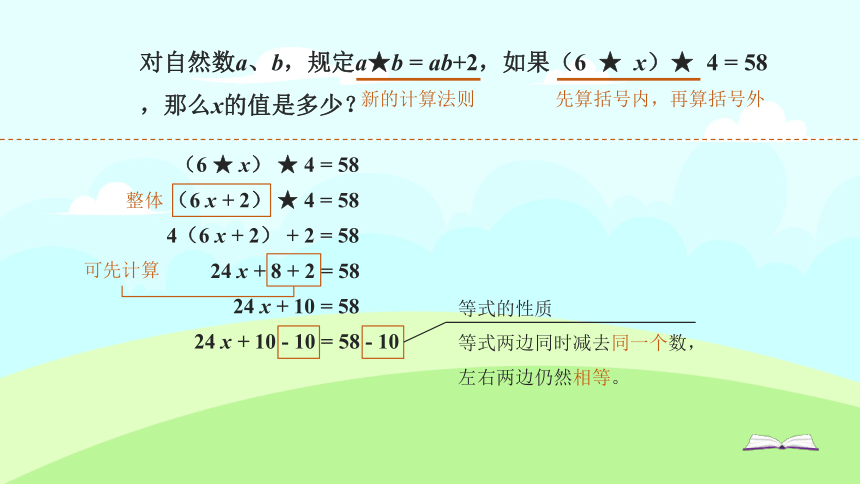
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
新的计算法则
先算括号内,再算括号外
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
整体
可先计算
等式的性质
等式两边同时减去同一个数,
左右两边仍然相等。
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
新的计算法则
先算括号内,再算括号外
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
24 x = 48
24 x ÷24 = 48 ÷24
x = 2
等式的性质
等式两边同时除以同一个不为0的数,左右两边仍然相等。
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
24 x = 48
24 x ÷24 = 48 ÷24
x = 2
24 x + 10 = 58
24 x = 58 - 10
“移项变号”
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
24 x = 48
24 x ÷24 = 48 ÷24
x = 2
24 x = 48
x = 48 ÷24
“移项变号”
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
24 x = 48
24 x ÷24 = 48 ÷24
x = 2
方法总结
把一个式子(或数)从等号的一边移动到另一边,原来的运算都要变成它的逆运算,这叫做移项变号法。
方程 x + 3 = 10 与 mx = 21有相同的解,求 m 的值。
解: x + 3 = 10
x + 3 – 3 = 10 - 3
x = 7
把x = 7 带入 mx = 21这个算式中
则 7m = 21
7m÷7 = 21÷7
m = 3
方法总结
对于含有两个未知数的方程,可先求出其中一个隐含在已知条件中的未知数的值,再求出另一个未知数的值。
解方程:4×[2(x -16)] = 8
解: 4× [2(x -16)] = 8
4× [2(x -16)] ÷4 = 8÷4
2(x -16)= 2
2(x -16)÷2 = 2 ÷2
x -16 = 1
x -16 + 16 = 1 + 16
x = 17
方法一
看成整体
看成整体
解方程:4× [2(x -16)] = 8
方法二
解: 4 ×[2(x -16)] = 8
8(x -16)= 8
8x -128 = 8
8x -128 + 128 = 8 + 128
8x = 136
8x ÷8 = 136 ÷8
x = 17
看成整体
已知 a + b = 35 , a – b = 25,求 a 和b 的值。
方法一
代入法
a + b = 35
a + b – b = 35 – b
a = 35 – b
把a = 35 – b 代入a – b = 25得
a – b = 25
35 – b – b = 25
35 – 2b = 25
35 – 2b + 2b = 25 + 2b
35 = 25 + 2b
35 – 25 = 25 + 2b – 25
10 = 2b
10 ÷2 = 2b ÷2
5 = b
b = 5
把b = 5 代入a = 35 – b得
a = 35 – b
a = 35 – 5
a = 30
已知 a + b = 35 , a – b = 25,求 a 和b 的值。
方法二
抵消法
a + b = 35
a – b = 25
a + b + a – b = 35 + 25
2a = 60
2a ÷2 = 60 ÷2
a = 30
把a = 30 代入a + b = 35得
30 + b = 35
30 + b – 30 = 35 – 30
b = 5
已知 a + b = 35 , a – b = 25,求 a 和b 的值。
方法二
抵消法
方法提示
当未知数多于一个时,根据等式的性质,把两个未知数转化为一个未知数,进行求解。
方法一
代入法
下次再见
奇怪的方程
—解方程
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
新的计算法则
先算括号内,再算括号外
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
整体
可先计算
等式的性质
等式两边同时减去同一个数,
左右两边仍然相等。
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
新的计算法则
先算括号内,再算括号外
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
24 x = 48
24 x ÷24 = 48 ÷24
x = 2
等式的性质
等式两边同时除以同一个不为0的数,左右两边仍然相等。
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
24 x = 48
24 x ÷24 = 48 ÷24
x = 2
24 x + 10 = 58
24 x = 58 - 10
“移项变号”
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
24 x = 48
24 x ÷24 = 48 ÷24
x = 2
24 x = 48
x = 48 ÷24
“移项变号”
对自然数a、b,规定a★b = ab+2,如果(6 ★ x)★ 4 = 58,那么x的值是多少?
(6 ★ x) ★ 4 = 58
(6 x + 2) ★ 4 = 58
4(6 x + 2) + 2 = 58
24 x + 8 + 2 = 58
24 x + 10 = 58
24 x + 10 - 10 = 58 - 10
24 x = 48
24 x ÷24 = 48 ÷24
x = 2
方法总结
把一个式子(或数)从等号的一边移动到另一边,原来的运算都要变成它的逆运算,这叫做移项变号法。
方程 x + 3 = 10 与 mx = 21有相同的解,求 m 的值。
解: x + 3 = 10
x + 3 – 3 = 10 - 3
x = 7
把x = 7 带入 mx = 21这个算式中
则 7m = 21
7m÷7 = 21÷7
m = 3
方法总结
对于含有两个未知数的方程,可先求出其中一个隐含在已知条件中的未知数的值,再求出另一个未知数的值。
解方程:4×[2(x -16)] = 8
解: 4× [2(x -16)] = 8
4× [2(x -16)] ÷4 = 8÷4
2(x -16)= 2
2(x -16)÷2 = 2 ÷2
x -16 = 1
x -16 + 16 = 1 + 16
x = 17
方法一
看成整体
看成整体
解方程:4× [2(x -16)] = 8
方法二
解: 4 ×[2(x -16)] = 8
8(x -16)= 8
8x -128 = 8
8x -128 + 128 = 8 + 128
8x = 136
8x ÷8 = 136 ÷8
x = 17
看成整体
已知 a + b = 35 , a – b = 25,求 a 和b 的值。
方法一
代入法
a + b = 35
a + b – b = 35 – b
a = 35 – b
把a = 35 – b 代入a – b = 25得
a – b = 25
35 – b – b = 25
35 – 2b = 25
35 – 2b + 2b = 25 + 2b
35 = 25 + 2b
35 – 25 = 25 + 2b – 25
10 = 2b
10 ÷2 = 2b ÷2
5 = b
b = 5
把b = 5 代入a = 35 – b得
a = 35 – b
a = 35 – 5
a = 30
已知 a + b = 35 , a – b = 25,求 a 和b 的值。
方法二
抵消法
a + b = 35
a – b = 25
a + b + a – b = 35 + 25
2a = 60
2a ÷2 = 60 ÷2
a = 30
把a = 30 代入a + b = 35得
30 + b = 35
30 + b – 30 = 35 – 30
b = 5
已知 a + b = 35 , a – b = 25,求 a 和b 的值。
方法二
抵消法
方法提示
当未知数多于一个时,根据等式的性质,把两个未知数转化为一个未知数,进行求解。
方法一
代入法
下次再见
