人教版 三年级下册数学 8、数学广角——搭配(二) 练习二十二 课件(共21张PPT)
文档属性
| 名称 | 人教版 三年级下册数学 8、数学广角——搭配(二) 练习二十二 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 10:05:36 | ||
图片预览






文档简介
(共21张PPT)
人教版数学三年级(下)
练习二十二
数学广角——搭配(二)
8
重点回顾
如何解决稍复杂的排列问题?
以组数问题为例,要做到不重复、不遗漏,可以用列举的方法,先考虑高位,再考虑低位,有顺序地依次排列,一一列举出所有的情况。
注意:0在组数时,不能在首位。
如何解决简单的搭配问题?
1.解决简单的搭配问题,可以用图形、符号、字母等表示实物,再用连线表示不同的搭配方法。
2.搭配时,可以从不同的角度考虑,比如先固定一个,再按顺序一一去搭配另一个。
3.求上装和下装的搭配方法种数时,如果上装有m件,下装有n件,那么一共就有m×n种搭配方法。
如何解决稍复杂的组合问题?
1.解决稍复杂的组合问题时,可以借助图片连线的方法来完成。
2.组合中不考虑事物的先后顺序,只需注意事物的不同元素。
练习巩固
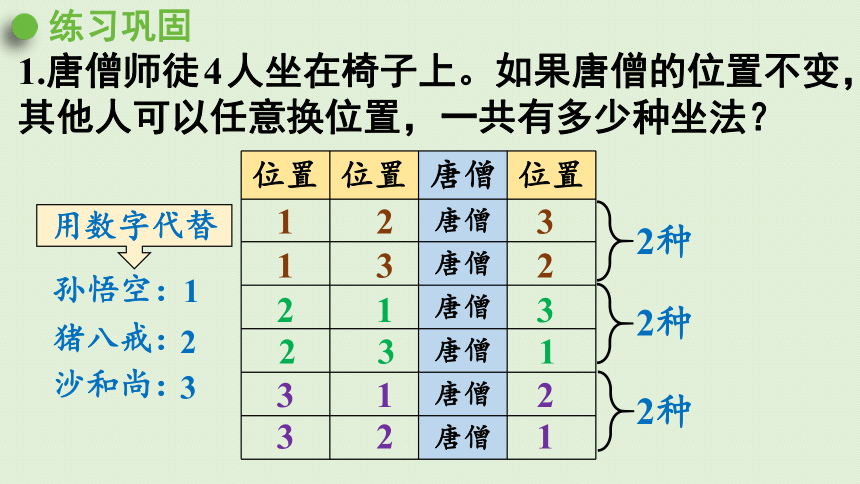
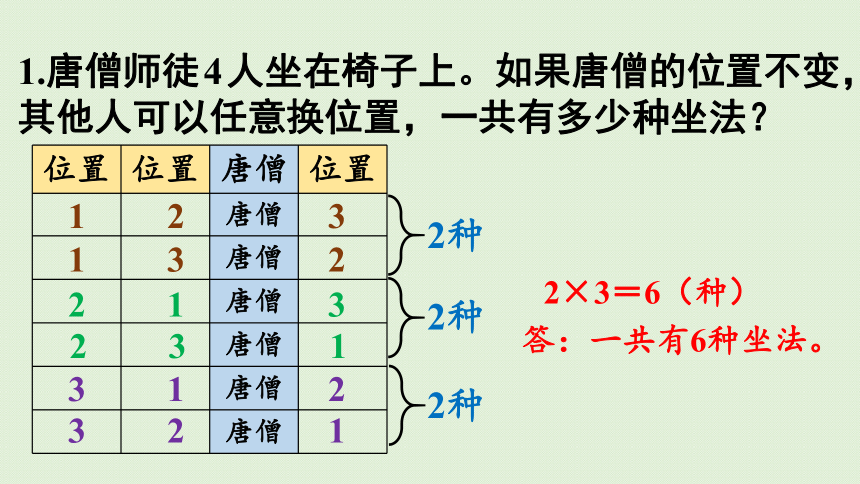
1.唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意换位置,一共有多少种坐法?
孙悟空:
1
猪八戒:
2
沙和尚:
3
位置 位置 唐僧 位置
唐僧
唐僧
唐僧
唐僧
唐僧
唐僧
1
2
3
1
3
2
2
1
3
2
3
1
3
1
2
3
2
1
2种
2种
用数字代替
2种
2×3=6(种)
答:一共有6种坐法。
位置 位置 唐僧 位置
唐僧
唐僧
唐僧
唐僧
唐僧
唐僧
1
2
3
1
3
2
2
1
3
2
3
1
3
1
2
3
2
1
2种
2种
2种
1.唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意换位置,一共有多少种坐法?
十位 个位
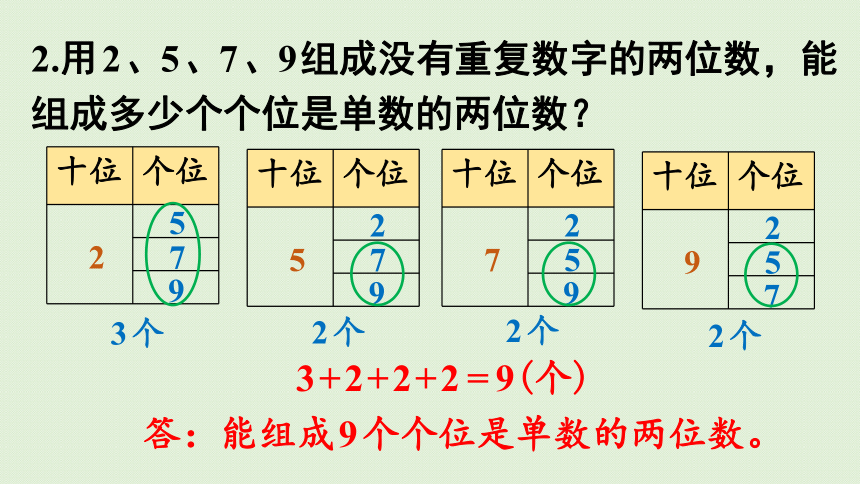
2.用2、5、7、9组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
2
2个
2个
2个
3+2+2+2=9(个)
答:能组成9个个位是单数的两位数。
5
7
9
十位 个位
5
2
7
9
十位 个位
7
2
5
9
十位 个位
9
2
5
7
3个
3.把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
只有有害、厨余和可回收物垃圾桶才能摆在最左边
① ② ③ ④
当有害垃圾桶在最左边时,有6种摆法。
① ② ③ ④
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有( )种摆法。
① ② ③ ④
有害
6
有( )种摆法。
① ② ③ ④
厨余
6
有( )种摆法。
① ② ③ ④
可回收
6
6+6+6=18(种)
答:一共有18种摆法。
4.
男孩 女孩1 女孩2 女孩3
聪聪 明明
答:一共要拍8张照片。
2×4=8(种)
5.右图中一共有多少个长方形?
①由一个长方形组成的:
4个
②由两个长方形组成的:
4个
③由四个长方形组成的:
1个
4+4+1=9(个)
答:一共有9个长方形。
③
①
②
④
①
②
③
④
⑤
⑥
路线一:①③⑤
路线二:①③⑥
路线五:②③⑤
路线六:②③⑥
路线三:①④⑤
路线四:①④⑥
路线七:②④⑤
路线八:②④⑥
答:共有8条路线。
6.从鸟岛到狮虎山,共有多少条路线
鸟岛
猴山
大象馆
狮虎山
7.甲、乙、丙、丁4个人参加乒乓球小组赛,每2个人比赛一场,一共要比赛多少场?
甲 乙 丙 丁
①
②
③
④
⑤
⑥
答:一共要比赛6场。
8.
(1)小明想从中任选2本,共有多少种选法?
答:共有6种选法。搭配如下:
①
②
③
④
①②、①③、①④、②③、②④、③④。
(2)小明想选《数学家的故事》和1本其他的书,分别送给小红和小丽,共有多少种送法?
组合 小红 小丽
答:共有6种选法。
①
②
③
④
①
②
①
②
②
①
①
③
①
③
①
③
①
④
①
④
④
①
8.
9.按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
(1)小于1而小数部分是三位数的小数。
0.576 0.567 0.756 0.765 0.657 0.675
7.506 7.560 7.056 7.065 7.650 7.605
(2)大于7而小数部分是三位数的小数。
要求写小于1而小数部分是三位的小数,也就是整数部分是0,其他三个数字有序地排列在小数部分。
要求写大于7而小数部分是三位的小数,也就是整数部分是7,其他三个数字有序地排列在小数部分。
10.从100到300的数中,有多少个十位和个位相同的数?
百 十 个
0 0
1
1 1 1
1 2 2
1 3 3
1 4 4
1 5 5
1 6 6
1 7 7
1 8 8
1 9 9
10
答:有21个十位和个位相同的数。
先确定百位数字,再看十位和百位相同的组合有多少种。
百位上是2时也是10个,再加上300这个数,共21个。
拓展提升
玩扑克游戏。从下面的4张扑克牌中,每次选出两张扑克牌,将上面的数字相加,可以得到多少个不同的和 将上面的数字相减,可以得到多少个不同的差
用列表法有序计算,再划去重复的和(差),如:
和
6
7
8
9
6
7
8
9
13
14
15
13
15
16
14
15
17
15
16
17
得到的和有13、14、15、16、17,共5种。
差
6
7
8
9
6
7
8
9
1
2
3
1
1
2
2
1
1
3
2
1
得到的差有1、2、3,共3种。
答:可以得到5种不同的和,3种不同的差。
归 纳 总 结
解决这种组合后满足一定条件的题目时,可以先组合,再根据条件筛选符合题意的组合。
人教版数学三年级(下)
练习二十二
数学广角——搭配(二)
8
重点回顾
如何解决稍复杂的排列问题?
以组数问题为例,要做到不重复、不遗漏,可以用列举的方法,先考虑高位,再考虑低位,有顺序地依次排列,一一列举出所有的情况。
注意:0在组数时,不能在首位。
如何解决简单的搭配问题?
1.解决简单的搭配问题,可以用图形、符号、字母等表示实物,再用连线表示不同的搭配方法。
2.搭配时,可以从不同的角度考虑,比如先固定一个,再按顺序一一去搭配另一个。
3.求上装和下装的搭配方法种数时,如果上装有m件,下装有n件,那么一共就有m×n种搭配方法。
如何解决稍复杂的组合问题?
1.解决稍复杂的组合问题时,可以借助图片连线的方法来完成。
2.组合中不考虑事物的先后顺序,只需注意事物的不同元素。
练习巩固
1.唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意换位置,一共有多少种坐法?
孙悟空:
1
猪八戒:
2
沙和尚:
3
位置 位置 唐僧 位置
唐僧
唐僧
唐僧
唐僧
唐僧
唐僧
1
2
3
1
3
2
2
1
3
2
3
1
3
1
2
3
2
1
2种
2种
用数字代替
2种
2×3=6(种)
答:一共有6种坐法。
位置 位置 唐僧 位置
唐僧
唐僧
唐僧
唐僧
唐僧
唐僧
1
2
3
1
3
2
2
1
3
2
3
1
3
1
2
3
2
1
2种
2种
2种
1.唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意换位置,一共有多少种坐法?
十位 个位
2.用2、5、7、9组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
2
2个
2个
2个
3+2+2+2=9(个)
答:能组成9个个位是单数的两位数。
5
7
9
十位 个位
5
2
7
9
十位 个位
7
2
5
9
十位 个位
9
2
5
7
3个
3.把下边4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
只有有害、厨余和可回收物垃圾桶才能摆在最左边
① ② ③ ④
当有害垃圾桶在最左边时,有6种摆法。
① ② ③ ④
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有害
厨余
可回收物
其他
有( )种摆法。
① ② ③ ④
有害
6
有( )种摆法。
① ② ③ ④
厨余
6
有( )种摆法。
① ② ③ ④
可回收
6
6+6+6=18(种)
答:一共有18种摆法。
4.
男孩 女孩1 女孩2 女孩3
聪聪 明明
答:一共要拍8张照片。
2×4=8(种)
5.右图中一共有多少个长方形?
①由一个长方形组成的:
4个
②由两个长方形组成的:
4个
③由四个长方形组成的:
1个
4+4+1=9(个)
答:一共有9个长方形。
③
①
②
④
①
②
③
④
⑤
⑥
路线一:①③⑤
路线二:①③⑥
路线五:②③⑤
路线六:②③⑥
路线三:①④⑤
路线四:①④⑥
路线七:②④⑤
路线八:②④⑥
答:共有8条路线。
6.从鸟岛到狮虎山,共有多少条路线
鸟岛
猴山
大象馆
狮虎山
7.甲、乙、丙、丁4个人参加乒乓球小组赛,每2个人比赛一场,一共要比赛多少场?
甲 乙 丙 丁
①
②
③
④
⑤
⑥
答:一共要比赛6场。
8.
(1)小明想从中任选2本,共有多少种选法?
答:共有6种选法。搭配如下:
①
②
③
④
①②、①③、①④、②③、②④、③④。
(2)小明想选《数学家的故事》和1本其他的书,分别送给小红和小丽,共有多少种送法?
组合 小红 小丽
答:共有6种选法。
①
②
③
④
①
②
①
②
②
①
①
③
①
③
①
③
①
④
①
④
④
①
8.
9.按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
(1)小于1而小数部分是三位数的小数。
0.576 0.567 0.756 0.765 0.657 0.675
7.506 7.560 7.056 7.065 7.650 7.605
(2)大于7而小数部分是三位数的小数。
要求写小于1而小数部分是三位的小数,也就是整数部分是0,其他三个数字有序地排列在小数部分。
要求写大于7而小数部分是三位的小数,也就是整数部分是7,其他三个数字有序地排列在小数部分。
10.从100到300的数中,有多少个十位和个位相同的数?
百 十 个
0 0
1
1 1 1
1 2 2
1 3 3
1 4 4
1 5 5
1 6 6
1 7 7
1 8 8
1 9 9
10
答:有21个十位和个位相同的数。
先确定百位数字,再看十位和百位相同的组合有多少种。
百位上是2时也是10个,再加上300这个数,共21个。
拓展提升
玩扑克游戏。从下面的4张扑克牌中,每次选出两张扑克牌,将上面的数字相加,可以得到多少个不同的和 将上面的数字相减,可以得到多少个不同的差
用列表法有序计算,再划去重复的和(差),如:
和
6
7
8
9
6
7
8
9
13
14
15
13
15
16
14
15
17
15
16
17
得到的和有13、14、15、16、17,共5种。
差
6
7
8
9
6
7
8
9
1
2
3
1
1
2
2
1
1
3
2
1
得到的差有1、2、3,共3种。
答:可以得到5种不同的和,3种不同的差。
归 纳 总 结
解决这种组合后满足一定条件的题目时,可以先组合,再根据条件筛选符合题意的组合。
