高二上学期物理粤教版(2019)选择性必修第二册专题一 带电粒子在磁场中的运动 同步练习(word版含答案)
文档属性
| 名称 | 高二上学期物理粤教版(2019)选择性必修第二册专题一 带电粒子在磁场中的运动 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 451.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-11 11:22:01 | ||
图片预览




文档简介
带电粒子在磁场中的运动(不计重力)
一、选择题
【中垂线类】
1.如图所示,MN为铝质薄平板,铝板上方和下方分别有垂直于图平面的匀强磁场(未面出),一带电粒子从紧贴铝板上表面的P点垂直于铝板向上射出,从Q点穿越铝板后到达PQ的中点O,已知粒子穿越铝板时,其动能损失一半,速度方向和电荷量不变.不计重力.铝板上方和下方的磁感应强度大小之比为( )
A.2 B.
C.1 D.
2.如图所示的虚线框为一长方形区域,该区域内有一垂直于纸面向里的匀强磁场,一束电子以不同的速率从O点垂直于磁场方向、沿图中方向射入磁场后,分别从a、b、c、d四点射出磁场,比较它们在磁场中的运动时间ta、tb、tc、td,其大小关系是( )
A.taC.ta=tbtc>td
3.(多选)如图所示,一单边有界匀强磁场的边界上有一粒子源,以与水平方向成θ角的不同速率向磁场中射入两个相同的粒子1和2,粒子1经磁场偏转后从边界上A点射出磁场,粒子2经磁场偏转后从边界B点射出磁场,OA=AB,则( )
A.粒子1与粒子2的速率之比为1:2
B.粒子1与粒子2的速率之比为1:4
C.粒子1与粒子2在磁场中运动的时间之比为1:1
D.粒子1与粒子2在磁场中运动的时间之比为1:2
4.(多选)利用如图所示装置可以选择一定速度范围内的带电粒子。图中板MN上方是磁感应强度大小为B、方向垂直纸面向里的匀强磁场,板上有两条宽度分别为2d和d的缝,两缝近端相距为L。一群质量为m、电荷量为q,具有不同速度的粒子从宽度为2d的缝垂直于板MN进入磁场,对于能够从宽度为d的缝射出的粒子,下列说法正确的是( )
A.粒子带正电
B.射出粒子的最大速度为
C.保持d和L不变,增大B,射出粒子的最大速度与最小速度之差增大
D.保持d和B不变,增大L,射出粒子的最大速度与最小速度之差增大
【速度偏转角类】
5.如图所示,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外.一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为 ,已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( )
A.
B.
C.
D.
6.如图所示,在垂直纸面向里的匀强磁场的边界上,有两个质量和电量均相同的正、负离子(不计重力),从点O以相同的速度先后射入磁场中,入射方向与边界成θ角,则正、负离子在磁场中运动不正确的是( )
A.运动时间相同
B.运动轨迹的半径相同
C.重新回到边界时速度的大小和方向相同
D.重新回到边界的位置与O点距离相等
7.(多选)如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直但方向相反的匀强磁场,区域Ⅱ内磁感应强度是区域Ⅰ内磁感应强度的2倍,一带电粒子在区域Ⅰ左侧边界处以垂直边界的速度进入区域Ⅰ,发现粒子离开区域Ⅰ时速度方向改变了30°,然后进入区域Ⅱ,测得粒子在区域Ⅱ内的运动时间与区域Ⅰ内的运动时间相等,则下列说法正确的是( )
A.粒子在区域Ⅰ和区域Ⅱ中的速率之比为1:1
B.粒子在区域Ⅰ和区域Ⅱ中的角速度之比为2:1
C.粒子在区域Ⅰ和区域Ⅱ中的圆心角之比为1:2
D.区域Ⅰ和区域Ⅱ的宽度之比为1:1
8.(多选)如图所示,左右边界分别为PP′、QQ′的匀强磁场的宽度为d,磁感应强度大小为B,方向垂直纸面向里。一个质量为m、电荷量大小为q的微观粒子,沿与左边界PP′成θ=45°方向以速度v0垂直射入磁场。不计粒子重力,欲使粒子不从边界QQ′射出,v0的最大值可能是( )
A. B.
C. D.
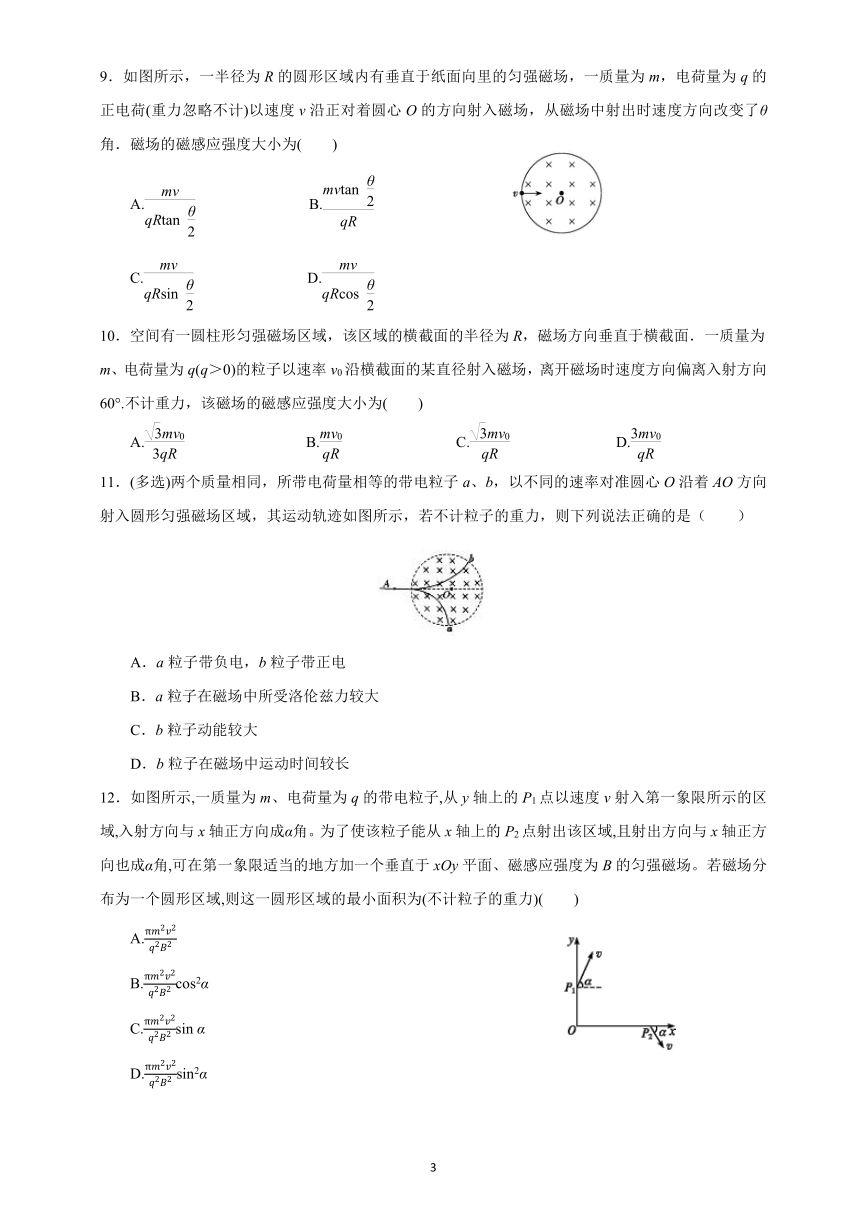
9.如图所示,一半径为R的圆形区域内有垂直于纸面向里的匀强磁场,一质量为m,电荷量为q的正电荷(重力忽略不计)以速度v沿正对着圆心O的方向射入磁场,从磁场中射出时速度方向改变了θ角.磁场的磁感应强度大小为( )
A. B.
C. D.
10.空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直于横截面.一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°.不计重力,该磁场的磁感应强度大小为( )
A. B. C. D.
11.(多选)两个质量相同,所带电荷量相等的带电粒子a、b,以不同的速率对准圆心O沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图所示,若不计粒子的重力,则下列说法正确的是( )
A.a粒子带负电,b粒子带正电
B.a粒子在磁场中所受洛伦兹力较大
C.b粒子动能较大
D.b粒子在磁场中运动时间较长
12.如图所示,一质量为m、电荷量为q的带电粒子,从y轴上的P1点以速度v射入第一象限所示的区域,入射方向与x轴正方向成α角。为了使该粒子能从x轴上的P2点射出该区域,且射出方向与x轴正方向也成α角,可在第一象限适当的地方加一个垂直于xOy平面、磁感应强度为B的匀强磁场。若磁场分布为一个圆形区域,则这一圆形区域的最小面积为(不计粒子的重力)( )
A.
B.cos2α
C.sin α
D.sin2α
【定圆旋转法类】
13.(多选)如图所示,在直线MN上方存在着垂直于纸面向里的匀强磁场,放置在直线MN上P点的粒子源(粒子均带负电),可以向磁场区域纸面内的各个方向发射出比荷k和速率v均相同的粒子,PQ间距离等于粒子的轨道半径R,则过Q点的粒子的运动时间为( )
A.
B.
C.
D.
14.(多选)如图所示,边长为L的正三角形ABC区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B0,BC边的中点O有一粒子源,可以在ABC平面内沿任意方向发射速率为v的相同的带正电的粒子,若从AB边中点D射出磁场的粒子,从O到D的过程中速度方向偏转了60°,不计粒子的重力及带电粒子之间的相互作用力,下列说法正确的是( )
A.粒子运动的轨迹半径为L
B.粒子不可能从A点射出磁场
C.粒子的比荷=
D.从B点射出的粒子在磁场中的运动时间为
15.(多选)如图所示,在半径为R的圆形区域内有匀强磁场,磁感应强度为B,方向垂直于圆平面(未画出)。一群比荷为的负离子以相同速率v0(较大)由P点在纸平面内向不同方向射入磁场中发生偏转后,又飞出磁场,则下列说法正确的是(不计离子重力)( )
A.离子飞出磁场时的动能一定相等
B.离子在磁场中运动半径一定相等
C.由Q点飞出的离子在磁场中运动的时间最长
D.沿PQ方向射入的离子飞出时偏转角最大
16.(多选)如图所示,宽d=4 cm的有界匀强磁场,纵向范围足够大,磁场方向垂直于纸面向里.现有一群正粒子从O点以相同的速率在纸面内沿不同方向进入磁场,若粒子在磁场中做匀速圆周运动的轨道半径为r=10 cm,则( )
A.右边界-8 cmB.右边界0C.左边界y>16 cm处有粒子射出
D.左边界017.如图所示,MN是一荧光屏,当带电粒子打到荧光屏上时,荧光屏能够发光。MN的上方有磁感应强度为B的匀强磁场,磁场方向垂直纸面向里。P为屏上的一小孔,PQ与MN垂直。一束质量为m、电荷量为+q或-q的两种粒子(不计重力),以相同的速率v,从小孔 P处沿垂直于磁场且与PQ夹角为θ的范围内向各个方向射入磁场区域,不计粒子间的相互作用。则以下说法正确的是( )
A.在荧光屏上P点两侧将出现两个相等长度的条形亮线,其长度为(1-cos θ)
B.在荧光屏上P点两侧将出现两个相等长度的条形亮线,其长度为(1-sin θ)
C.在荧光屏上将出现一个圆形亮斑,其半径为
D.在荧光屏上将出现一个圆形亮环,其外半径为,内半径为cos θ
18.(多选)如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a。在O点放置一个粒子源,可以向各个方向发射某种带负电的粒子,粒子的比荷为,发射速度大小都为v0,且满足v0=,发射方向由图中的角度θ表示。对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
A.粒子有可能打到A点
B.以θ=60°飞入的粒子在磁场中运动时间最短
C.以θ<30°飞入的粒子在磁场中运动的时间都相等
D.在AC边界上只有一半区域有粒子射出
【缩放圆类】
19.如图所示,在x>0,y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B,现有一质量为m、电荷量为q的带正电粒子,从x轴上的某点P沿着与x轴成30°角的方向射入磁场,不计重力的影响,则下列有关说法中正确的是( )
A.只要粒子的速率合适,粒子就可能通过坐标原点
B.粒子在磁场中运动所经历的时间一定为
C.粒子在磁场中运动所经历的时间可能为
D.粒子在磁场中运动所经历的时间可能为
二、非选择题
20.如图所示,在直角三角形OPN区域内存在匀强磁场,磁感应强度大小为B、方向垂直于纸面向外。一带正电的粒子从静止开始经电压U加速后,沿平行于x轴的方向射入磁场;一段时间后,该粒子在OP边上某点以垂直于x轴的方向射出。已知O点为坐标原点,N点在y轴上,OP与x轴的夹角为30°,粒子进入磁场的入射点与离开磁场的出射点之间的距离为d,不计重力。求:
(1)带电粒子的比荷;
(2)带电粒子从射入磁场到运动至x轴的时间。
21.如图所示,在光滑水平面上,存在着垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ,O、M、P、Q为磁场边界和x轴的交点,OM=MP=L.一质量为m、带电荷量为+q的带电小球,从原点O处,以速度大小为v0,与x轴正向成45°射入区域Ⅰ,又从M点射出区域Ⅰ(粒子的重力忽略不计).
(1)求区域Ⅰ的磁感应强度大小及方向;
(2)若带电小球能再次回到原点O,则匀强磁场Ⅱ的宽度需满足什么条件?小球两次经过原点O的时间间隔为多少?
22.如图甲所示,在y轴右侧加有垂直纸面向外的匀强磁场,磁感应强度B=1 T。从原点O处向第Ⅰ象限发射一比荷=1×104 C/kg的带正电的粒子(重力不计),速度大小v0=103 m/s,方向垂直于磁场且与x轴正方向成30°角。
(1)求粒子在该匀强磁场中做匀速圆周运动的半径R和在该磁场中运动的时间t1。
(2)若磁场随时间变化的规律如图乙所示(垂直于纸面向外为正方向),t=×10-4 s后空间不存在磁场。在t=0时刻,粒子仍从O点以与原来相同的速度v0射入,求粒子从O点射出后第2次经过x轴时距离点O的距离。
参考答案:
一、选择题
1 2 3 4 5 6 7 8 9 10
D D AC BC B A ACD AC B A
11 12 13 14 15 16 17 18 19
AC D BC BC BC AD A AD C
二、非选择题
20.[答案] (1) (2)
[解析] (1)设带电粒子的质量为m,电荷量为q,加速后的速度大小为v。由动能定理有qU=mv2 ①
设粒子在磁场中做匀速圆周运动的半径为r,由洛伦兹力公式和牛顿第二定律有
qvB=m ②
由几何关系知d=r ③
联立①②③式得=。 ④
(2)由几何关系知,带电粒子射入磁场后运动到x轴所经过的路程为
s=+rtan 30° ⑤
带电粒子从射入磁场到运动至x轴的时间为
t= ⑥
联立②④⑤⑥式得t=。 ⑦
21.[答案] (1) (2)d≥(+1)L t总=
[解析] (1)小球进入区域Ⅰ做匀速圆周运动,由几何知识可得:
R1=L,由R1=,解得B=
(2)运动轨迹如图,在区域Ⅱ做匀速圆周运动的半径为:R2=L
由几何知识得d≥(+1)L
带电小球第一次在磁场Ⅰ运动时间t1=×=
带电小球第一次在空白区域运动时间t2=
带电小球在磁场Ⅱ运动时间t3=×=
小球两次经过原点O的时间间隔为t总=2(t1+t2)+t3=
22.[答案] (1)0.1 m π×10-4 s (2)0.6 m
[解析]
(1)轨迹如图(a)所示。由Bqv=m得
轨迹半径R==0.1 m
粒子运动周期T==2π×10-4 s (a)
粒子在磁场中轨迹所对的圆心角为240°,所以粒子在磁场中运动的时间为t1=π×10-4 s。
(2)磁场变化的半周期为Δt=×10-4 s=
在图(b)中,∠OO1C=∠CO2D=120°,且O1O2平行于x轴
OE=2(R+Rsin 30°)=3R=0.3 m
在Rt△EDP中,∠EDP=60°,DE=2Rsin 60°
EP=DEtan 60°=3R=0.3 m (b)
则粒子从O点射出后第2次经过x轴时距离点O的距离为OP=OE+EP=0.6 m。
一、选择题
【中垂线类】
1.如图所示,MN为铝质薄平板,铝板上方和下方分别有垂直于图平面的匀强磁场(未面出),一带电粒子从紧贴铝板上表面的P点垂直于铝板向上射出,从Q点穿越铝板后到达PQ的中点O,已知粒子穿越铝板时,其动能损失一半,速度方向和电荷量不变.不计重力.铝板上方和下方的磁感应强度大小之比为( )
A.2 B.
C.1 D.
2.如图所示的虚线框为一长方形区域,该区域内有一垂直于纸面向里的匀强磁场,一束电子以不同的速率从O点垂直于磁场方向、沿图中方向射入磁场后,分别从a、b、c、d四点射出磁场,比较它们在磁场中的运动时间ta、tb、tc、td,其大小关系是( )
A.ta
3.(多选)如图所示,一单边有界匀强磁场的边界上有一粒子源,以与水平方向成θ角的不同速率向磁场中射入两个相同的粒子1和2,粒子1经磁场偏转后从边界上A点射出磁场,粒子2经磁场偏转后从边界B点射出磁场,OA=AB,则( )
A.粒子1与粒子2的速率之比为1:2
B.粒子1与粒子2的速率之比为1:4
C.粒子1与粒子2在磁场中运动的时间之比为1:1
D.粒子1与粒子2在磁场中运动的时间之比为1:2
4.(多选)利用如图所示装置可以选择一定速度范围内的带电粒子。图中板MN上方是磁感应强度大小为B、方向垂直纸面向里的匀强磁场,板上有两条宽度分别为2d和d的缝,两缝近端相距为L。一群质量为m、电荷量为q,具有不同速度的粒子从宽度为2d的缝垂直于板MN进入磁场,对于能够从宽度为d的缝射出的粒子,下列说法正确的是( )
A.粒子带正电
B.射出粒子的最大速度为
C.保持d和L不变,增大B,射出粒子的最大速度与最小速度之差增大
D.保持d和B不变,增大L,射出粒子的最大速度与最小速度之差增大
【速度偏转角类】
5.如图所示,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外.一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为 ,已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( )
A.
B.
C.
D.
6.如图所示,在垂直纸面向里的匀强磁场的边界上,有两个质量和电量均相同的正、负离子(不计重力),从点O以相同的速度先后射入磁场中,入射方向与边界成θ角,则正、负离子在磁场中运动不正确的是( )
A.运动时间相同
B.运动轨迹的半径相同
C.重新回到边界时速度的大小和方向相同
D.重新回到边界的位置与O点距离相等
7.(多选)如图所示,在区域Ⅰ和区域Ⅱ内分别存在与纸面垂直但方向相反的匀强磁场,区域Ⅱ内磁感应强度是区域Ⅰ内磁感应强度的2倍,一带电粒子在区域Ⅰ左侧边界处以垂直边界的速度进入区域Ⅰ,发现粒子离开区域Ⅰ时速度方向改变了30°,然后进入区域Ⅱ,测得粒子在区域Ⅱ内的运动时间与区域Ⅰ内的运动时间相等,则下列说法正确的是( )
A.粒子在区域Ⅰ和区域Ⅱ中的速率之比为1:1
B.粒子在区域Ⅰ和区域Ⅱ中的角速度之比为2:1
C.粒子在区域Ⅰ和区域Ⅱ中的圆心角之比为1:2
D.区域Ⅰ和区域Ⅱ的宽度之比为1:1
8.(多选)如图所示,左右边界分别为PP′、QQ′的匀强磁场的宽度为d,磁感应强度大小为B,方向垂直纸面向里。一个质量为m、电荷量大小为q的微观粒子,沿与左边界PP′成θ=45°方向以速度v0垂直射入磁场。不计粒子重力,欲使粒子不从边界QQ′射出,v0的最大值可能是( )
A. B.
C. D.
9.如图所示,一半径为R的圆形区域内有垂直于纸面向里的匀强磁场,一质量为m,电荷量为q的正电荷(重力忽略不计)以速度v沿正对着圆心O的方向射入磁场,从磁场中射出时速度方向改变了θ角.磁场的磁感应强度大小为( )
A. B.
C. D.
10.空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直于横截面.一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°.不计重力,该磁场的磁感应强度大小为( )
A. B. C. D.
11.(多选)两个质量相同,所带电荷量相等的带电粒子a、b,以不同的速率对准圆心O沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图所示,若不计粒子的重力,则下列说法正确的是( )
A.a粒子带负电,b粒子带正电
B.a粒子在磁场中所受洛伦兹力较大
C.b粒子动能较大
D.b粒子在磁场中运动时间较长
12.如图所示,一质量为m、电荷量为q的带电粒子,从y轴上的P1点以速度v射入第一象限所示的区域,入射方向与x轴正方向成α角。为了使该粒子能从x轴上的P2点射出该区域,且射出方向与x轴正方向也成α角,可在第一象限适当的地方加一个垂直于xOy平面、磁感应强度为B的匀强磁场。若磁场分布为一个圆形区域,则这一圆形区域的最小面积为(不计粒子的重力)( )
A.
B.cos2α
C.sin α
D.sin2α
【定圆旋转法类】
13.(多选)如图所示,在直线MN上方存在着垂直于纸面向里的匀强磁场,放置在直线MN上P点的粒子源(粒子均带负电),可以向磁场区域纸面内的各个方向发射出比荷k和速率v均相同的粒子,PQ间距离等于粒子的轨道半径R,则过Q点的粒子的运动时间为( )
A.
B.
C.
D.
14.(多选)如图所示,边长为L的正三角形ABC区域内有垂直纸面向里的匀强磁场,磁感应强度大小为B0,BC边的中点O有一粒子源,可以在ABC平面内沿任意方向发射速率为v的相同的带正电的粒子,若从AB边中点D射出磁场的粒子,从O到D的过程中速度方向偏转了60°,不计粒子的重力及带电粒子之间的相互作用力,下列说法正确的是( )
A.粒子运动的轨迹半径为L
B.粒子不可能从A点射出磁场
C.粒子的比荷=
D.从B点射出的粒子在磁场中的运动时间为
15.(多选)如图所示,在半径为R的圆形区域内有匀强磁场,磁感应强度为B,方向垂直于圆平面(未画出)。一群比荷为的负离子以相同速率v0(较大)由P点在纸平面内向不同方向射入磁场中发生偏转后,又飞出磁场,则下列说法正确的是(不计离子重力)( )
A.离子飞出磁场时的动能一定相等
B.离子在磁场中运动半径一定相等
C.由Q点飞出的离子在磁场中运动的时间最长
D.沿PQ方向射入的离子飞出时偏转角最大
16.(多选)如图所示,宽d=4 cm的有界匀强磁场,纵向范围足够大,磁场方向垂直于纸面向里.现有一群正粒子从O点以相同的速率在纸面内沿不同方向进入磁场,若粒子在磁场中做匀速圆周运动的轨道半径为r=10 cm,则( )
A.右边界-8 cm
D.左边界0
A.在荧光屏上P点两侧将出现两个相等长度的条形亮线,其长度为(1-cos θ)
B.在荧光屏上P点两侧将出现两个相等长度的条形亮线,其长度为(1-sin θ)
C.在荧光屏上将出现一个圆形亮斑,其半径为
D.在荧光屏上将出现一个圆形亮环,其外半径为,内半径为cos θ
18.(多选)如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=a。在O点放置一个粒子源,可以向各个方向发射某种带负电的粒子,粒子的比荷为,发射速度大小都为v0,且满足v0=,发射方向由图中的角度θ表示。对于粒子进入磁场后的运动(不计重力作用),下列说法正确的是( )
A.粒子有可能打到A点
B.以θ=60°飞入的粒子在磁场中运动时间最短
C.以θ<30°飞入的粒子在磁场中运动的时间都相等
D.在AC边界上只有一半区域有粒子射出
【缩放圆类】
19.如图所示,在x>0,y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B,现有一质量为m、电荷量为q的带正电粒子,从x轴上的某点P沿着与x轴成30°角的方向射入磁场,不计重力的影响,则下列有关说法中正确的是( )
A.只要粒子的速率合适,粒子就可能通过坐标原点
B.粒子在磁场中运动所经历的时间一定为
C.粒子在磁场中运动所经历的时间可能为
D.粒子在磁场中运动所经历的时间可能为
二、非选择题
20.如图所示,在直角三角形OPN区域内存在匀强磁场,磁感应强度大小为B、方向垂直于纸面向外。一带正电的粒子从静止开始经电压U加速后,沿平行于x轴的方向射入磁场;一段时间后,该粒子在OP边上某点以垂直于x轴的方向射出。已知O点为坐标原点,N点在y轴上,OP与x轴的夹角为30°,粒子进入磁场的入射点与离开磁场的出射点之间的距离为d,不计重力。求:
(1)带电粒子的比荷;
(2)带电粒子从射入磁场到运动至x轴的时间。
21.如图所示,在光滑水平面上,存在着垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ,O、M、P、Q为磁场边界和x轴的交点,OM=MP=L.一质量为m、带电荷量为+q的带电小球,从原点O处,以速度大小为v0,与x轴正向成45°射入区域Ⅰ,又从M点射出区域Ⅰ(粒子的重力忽略不计).
(1)求区域Ⅰ的磁感应强度大小及方向;
(2)若带电小球能再次回到原点O,则匀强磁场Ⅱ的宽度需满足什么条件?小球两次经过原点O的时间间隔为多少?
22.如图甲所示,在y轴右侧加有垂直纸面向外的匀强磁场,磁感应强度B=1 T。从原点O处向第Ⅰ象限发射一比荷=1×104 C/kg的带正电的粒子(重力不计),速度大小v0=103 m/s,方向垂直于磁场且与x轴正方向成30°角。
(1)求粒子在该匀强磁场中做匀速圆周运动的半径R和在该磁场中运动的时间t1。
(2)若磁场随时间变化的规律如图乙所示(垂直于纸面向外为正方向),t=×10-4 s后空间不存在磁场。在t=0时刻,粒子仍从O点以与原来相同的速度v0射入,求粒子从O点射出后第2次经过x轴时距离点O的距离。
参考答案:
一、选择题
1 2 3 4 5 6 7 8 9 10
D D AC BC B A ACD AC B A
11 12 13 14 15 16 17 18 19
AC D BC BC BC AD A AD C
二、非选择题
20.[答案] (1) (2)
[解析] (1)设带电粒子的质量为m,电荷量为q,加速后的速度大小为v。由动能定理有qU=mv2 ①
设粒子在磁场中做匀速圆周运动的半径为r,由洛伦兹力公式和牛顿第二定律有
qvB=m ②
由几何关系知d=r ③
联立①②③式得=。 ④
(2)由几何关系知,带电粒子射入磁场后运动到x轴所经过的路程为
s=+rtan 30° ⑤
带电粒子从射入磁场到运动至x轴的时间为
t= ⑥
联立②④⑤⑥式得t=。 ⑦
21.[答案] (1) (2)d≥(+1)L t总=
[解析] (1)小球进入区域Ⅰ做匀速圆周运动,由几何知识可得:
R1=L,由R1=,解得B=
(2)运动轨迹如图,在区域Ⅱ做匀速圆周运动的半径为:R2=L
由几何知识得d≥(+1)L
带电小球第一次在磁场Ⅰ运动时间t1=×=
带电小球第一次在空白区域运动时间t2=
带电小球在磁场Ⅱ运动时间t3=×=
小球两次经过原点O的时间间隔为t总=2(t1+t2)+t3=
22.[答案] (1)0.1 m π×10-4 s (2)0.6 m
[解析]
(1)轨迹如图(a)所示。由Bqv=m得
轨迹半径R==0.1 m
粒子运动周期T==2π×10-4 s (a)
粒子在磁场中轨迹所对的圆心角为240°,所以粒子在磁场中运动的时间为t1=π×10-4 s。
(2)磁场变化的半周期为Δt=×10-4 s=
在图(b)中,∠OO1C=∠CO2D=120°,且O1O2平行于x轴
OE=2(R+Rsin 30°)=3R=0.3 m
在Rt△EDP中,∠EDP=60°,DE=2Rsin 60°
EP=DEtan 60°=3R=0.3 m (b)
则粒子从O点射出后第2次经过x轴时距离点O的距离为OP=OE+EP=0.6 m。
同课章节目录
- 第一章 磁场
- 第一节 安培力
- 第二节 安培力的应用
- 第三节 洛伦兹力
- 第四节 洛伦兹力与现代技术
- 第二章 电磁感应
- 第一节 感应电流的方向
- 第二节 法拉第电磁感应定律
- 第三节 电磁感应定律的应用
- 第四节 互感和自感
- 第五节 涡流现象及其应用
- 第三章 交变电流
- 第一节 认识交变电流
- 第二节 描述交变电流的物理量
- 第三节 变压器
- 第四节 远距离输电
- 第四章 电磁震荡与电磁波
- 第一节 电磁振动
- 第二节 麦克斯韦电磁电磁场理论
- 第三节 电磁波的发射、传播和接收
- 第四节 电磁波谱
- 第五章 传感器
- 第一节 传感器及其工作原理
- 第二节 传感器的应用
- 第三节 用传感器制作自动控制装置
- 第四节 利用智能手机中的磁传感器研究磁现象
