2021-2022学年华师大版八年级数学上册第14章勾股定理 单元综合达标测试(word版含答案)
文档属性
| 名称 | 2021-2022学年华师大版八年级数学上册第14章勾股定理 单元综合达标测试(word版含答案) | 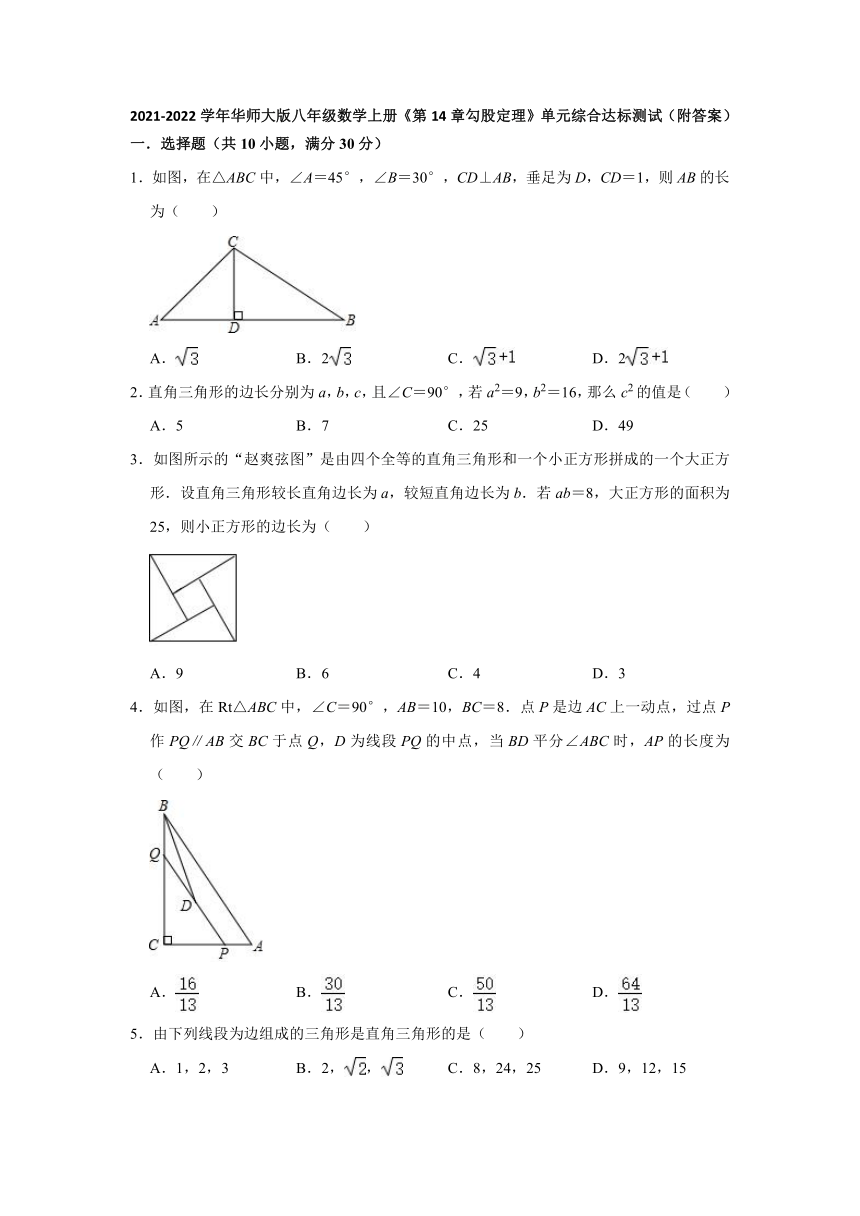 | |
| 格式 | doc | ||
| 文件大小 | 274.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 11:09:09 | ||
图片预览





文档简介
2021-2022学年华师大版八年级数学上册《第14章勾股定理》单元综合达标测试(附答案)
一.选择题(共10小题,满分30分)
1.如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为( )
A. B.2 C. D.2
2.直角三角形的边长分别为a,b,c,且∠C=90°,若a2=9,b2=16,那么c2的值是( )
A.5 B.7 C.25 D.49
3.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
4.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8.点P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当BD平分∠ABC时,AP的长度为( )
A. B. C. D.
5.由下列线段为边组成的三角形是直角三角形的是( )
A.1,2,3 B.2,, C.8,24,25 D.9,12,15
6.如图,根据下列条件,能判断△ABC是直角三角形的是( )
A.AB=32,BC=42,AC=52 B.(AB﹣BC)(AB+BC)=AC
C.AB=1,BC=,AC= D.∠B=3∠A,∠C=8∠A
7.下列几组数中的勾股数是( )
A.0.3,0.5,0.4 B.﹣3,4,5
C.6,8,12 D.24,7,25
8.如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的角平分线,则三角形ADC的面积为( )
A.3 B.10 C.12 D.15
9.如图,在灯塔O的东北方向8海里处有一轮船A,在灯塔的东南方向6海里处有一渔船B,则AB间的距离为( )
A.9海里 B.10海里 C.11海里 D.12海里
10.如图,圆柱的高为4cm,底面周长为6cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知长方形ADBC的边AD、BC恰好是上、下底面的直径,则蚂蚁要吃到食物,至少要爬行( )
A.4cm B.5cm C.7cm D.10cm
二.填空题(共6小题,满分30分)
11.如图,已知在Rt△ABC中,∠ACB=90°,分别以AC,BC,AB为直径作半圆,面积分别记为S1,S2,S3,若S3=9π,则S1+S2等于 .
12.在△ABC中,AB=AC=5cm,BC=8cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的方向运动.设运动时间为t,如果过D、P两点的直线将△ABC的面积分成两个部分,使其中一部分是另一部分的2倍,那么t= 秒.
13.把图1中长和宽分别6和4的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2的正方形,则图2中小正方形ABCD的面积为 .
14.以直角三角形的三边分别向外作正方形,正方形A,B的面积分别是8cm2,10cm2,则正方形C的面积是 cm2.
15.如图,在5×2的正方形网格中,点A,P,B为格点,则∠APB= .
16.如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD= 度.
三.解答题(共9小题,满分60分)
17.如图,在△ABC中,AB=6,BC=8,AC=10.
(1)求证:△ABC是直角三角形;
(2)若AD平分∠BAC,求AD的长.
18.如图是由边长为1的小正方形拼成的网格.
(1)在图1网格中找格点P,使得AP与AB垂直.
(2)在图2网格中找格点P,使得△ABP的面积是3.
(3)在图3网格中找格点P,使得PA=PB.
19.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
(1)试说明a2+b2=c2;
(2)如果大正方形的面积是6,小正方形的面积是2,求(a+b)2的值.
20.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是近直角三角形,∠B>90°,∠C=50°,则∠A= .
(2)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,若CD是∠ACB的平分线.
①求证:△BDC为近直角三角形.
②求BD的长.
21.如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
22.如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.
(1)求∠ADC的度数;
(2)求出四边形ABCD的面积.
23.阅读下面材料:
勾股定理的逆定理:如果是直角三角形的三条边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.
能够成为直角三角形三条边长的正整数,称为勾股数.例如:32+42=52,3、4、5是一组勾股数.
古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2﹣1,c=m2+1,那么a,b,c为勾股数,你认为正确吗?如果正确,请说明理由,并利用这个结论得出一组勾股数.
24.如图,从电线杆离地面3米处向地面拉一条长为5米的拉线,这条拉线在地面的固定点距离电线杆底部有多少米?
25.如图,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,你能求出旗杆在离底部多少米的位置断裂吗?
参考答案
一.选择题(共10小题,满分30分)
1.解:在Rt△ACD中,∠A=45°,CD=1,
则AD=CD=1,
在Rt△CDB中,∠B=30°,CD=1,
则BD=,
故AB=AD+BD=+1.
故选:C.
2.解:∵∠C=90°,a2=9,b2=16,
∴c2=a2+b2=9+16=25.
故选:C.
3.解:由题意可知:中间小正方形的边长为:a﹣b,
∵每一个直角三角形的面积为:ab=×8=4,
∴4×ab+(a﹣b)2=25,
∴(a﹣b)2=25﹣16=9,
∴a﹣b=3,
故选:D.
4.解:设BQ=x,
在Rt△ABC中,∠C=90°,AB=10,BC=8,
由勾股定理得:AC===6,
∵BD平分∠ABC,
∴∠QBD=∠ABD,
∵PQ∥AB,
∴∠QDB=∠ABD,
∴∠QBD=∠QDB,
∴QD=BQ=x,
∵D为线段PQ的中点,
∴QP=2QD=2x,
∵PQ∥AB,
∴△CPQ∽△CAB,
∴==,即==,
解得:x=,CP=,
∴AP=CA﹣CP=,
故选:B.
5.解:12+22≠32,故选项A不符合题意;
22+()2≠()2,故选项B不符合题意;
82+242≠252,故选项C不符合题意;
92+122=152,故选项D符合题意;
故选:D.
6.解:A.∵AB=32=9,BC=42=16,AC=52=25,
∴AB2+BC2=92+162=337,AC2=252=625,
∴AB2+BC2≠AC2,
即△ABC不是直角三角形,故本选项不符合题意;
B.∵(AB﹣BC)(AB+BC)=AC,
∴AB2﹣BC2=AC,
即△ABC不是直角三角形,故本选项不符合题意;
C.∵AB=1,BC=,AC=,
∴AB2+BC2=12+()2=1+=,AC2=()2=,
∴AB2+BC2=AC2,
即△ABC是直角三角形,故本选项符合题意;
D.∵∠B=3∠A,∠C=8∠A,
又∵∠A+∠B+∠C=180°,
∴12∠A=180°,
∴∠A=15°,
∴最大角∠C=8∠A=120°>90°,
即△ABC不是直角三角形,故本选项不符合题意;
故选:C.
7.解:A、不是正整数,不是勾股数,不符合题意;
B、(﹣3)2+42=52,但不是正整数,不是勾股数,不符合题意;
C、62+82≠122,不是勾股数,不符合题意;
D、72+242=252,是勾股数,符合题意.
故选:D.
8.解:作DH⊥AC于H,如图,
在Rt△ABC中,∠B=90°,AB=6,BC=8,
∴AC==10,
∵AD为∠BAC的角平分线,
∴DB=DH,
∵×AB×CD=DH×AC,
∴6(8﹣DH)=10DH,解得DH=3,
∴S△ADC=×10×3=15.
故选:D.
9.解:已知东北方向和东南方向刚好是一直角,
∴∠AOB=90°,
又∵OA=8海里,OB=6海里,
∴AB==10(海里).
故选:B.
10.解:如图,将圆柱体沿着AC直线剪开,得到矩形,
则AB的长度为所求的最短距离,
根据题意圆柱的高为4cm,底面周长为6cm,
∴AC=4cm,BC=3cm,
根据勾股定理得:AB==5(cm),
∴蚂蚁要吃到食物,至少要爬行5cm,
故选:B.
二.填空题(共6小题,满分30分)
11.解:∵∠ACB=90°,
∴AC2+BC2=AB2,
∵S1=π()2×,S2=π()2×,S3=π()2×,
∴S1+S2=π()2×+π()2×=π()2×=S3,
∵S3=9π,
∴S1+S2=9π,
故答案为:9π.
12.解:分两种情况:
(1)P点在AB上时,如图1,过A作AD⊥BC于D,过P作PH⊥BC于H,
BP=t,
∵AB=AC=5cm,BC=8cm,D为BC的中点,
∴BD=BC=4,
∴AD===3,
设△BPD高为h,由2S△BPD=S△PDC,
2××4×h=×8×3﹣×4×h,
解得:h=2,
又∵∠PHB=∠ADB=90°,∠PBH=∠ABD,
∴t=(s);
(2)P点在AC上时,如图2,过A作AD⊥BC于D,过P作PH⊥BC于H,
同理可得h′=2,
∴CP=,
则t=5+5﹣=(s),
故答案为:或.
13.解:6﹣4=2,
2×2=4.
故图2中小正方形ABCD的面积为4.
故答案为:4.
14.解:根据题意得:SA+SB=SC,
∵正方形A,B的面积分别是8cm2,10cm2,
∴SC=8+10=18(cm2),
故答案为:18.
15.解:如图,延长AP交网格于点C,连接BC.
∵PC==,BC==,PB==,
∴PC=BC,PC2+BC2=PB2,
∴△PBC是等腰直角三角形,
∴∠BPC=45°,
∴∠APB=180°﹣∠BPC=135°.
故答案为:135°.
16.解:∵∠A=90°,AC=AB=4,
∴∠ACB=∠ABC=45°,
在Rt△ABC中,BC==4,
CD2+BC2=22+(4)2=36,BD2=62=36,
∴CD2+BC2=BD2,
∴∠BCD=90°,
∴∠ACD=45°,
故答案为:45.
三.解答题(共9小题,满分60分)
17.(1)证明:∵AB2+BC2=62+82=102=AC2,
∴∠B=90°,
∴△ABC是直角三角形;
(2)解:过D作DE⊥AC于E.
∵AD平分∠BAC,∠B=90°,
∴BD=DE,
在Rt△ABD中,AB=,
同理AE=,
∴AE=AB=6,
∴EC=AC﹣AE=4,
设BD=x,则DE=BD=x,CD=8﹣x,
∴x2+42=(8﹣x)2,
解得x=3,
∴AD===3.
18.解:(1)如图1,AP⊥AB.
(2)如图2,△ABP的面积==3.
∴格点P使得△ABP的面积是3(答案不唯一).
(3)如图3,∵PA==,PB==,
∴格点P使得PA=PB(答案不唯一).
19.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2.;
(2)由图可知,(b﹣a)2=2,4×ab=6﹣2=4,∴ab=2,
∴(a+b)2=(b﹣a)2+4ab=10.
20.解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为:20°;
(2)①如图1,设∠ACD=∠DCB=β,∠B=α,
则α+2β=90°,故△BDC是“近直角三角形”;
②如图2,过点D作DM⊥BC于点M,
∵CD平分∠ACB,DM⊥BC,DA⊥CA,
∴AD=DM.
在Rt△ACD和Rt△MCD中,
,
∴Rt△ACD≌Rt△MCD(HL).
∴AC=CM=4.
∵AB=3,AC=4,
∴BC===5.
∴BM=1.
设AD=DM=x,
∵DM2+BM2=DB2,
∴x2+12=(3﹣x)2,
∴x=,
∴BD=AB﹣AD=3﹣=.
21.解:连接BD,
在Rt△BAD中,
∵AB=AD=2,
∴∠ADB=45°,BD==2,
在△BCD中,
DB2+CD2=(2)2+12=9=CB2,
∴△BCD是直角三角形,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=45°+90°=135°.
22.解:(1)连接AC,在Rt△ABC中,∠ABC=90°,
∵AB=20cm,BC=15cm,
∴由勾股定理可得:AC===25(cm);
∵在△ADC中,CD=7cm,AD=24cm,
∴CD2+AD2=AC2,
∴∠ADC=90°;
(2)由(1)知,∠ADC=90°,
∴四边形ABCD的面积=S△ABC+S△ACD=+=234(cm2).
23.解:正确.理由:
∵m表示大于1的整数,
∴a,b,c都是正整数,且c是最大边,
∵(2m)2+(m2﹣1)2=(m2+1)2,
∴a2+b2=c2,
即a、b、c为勾股数.
当m=2时,可得一组勾股数3,4,5.
24.解:在Rt△ABC中,BC=3,AB=5,
由勾股定理,得AC2=AB2﹣BC2=52﹣32=42,
所以AC=4(米).
所以地面拉线固定点A到电线杆底部的距离为4米.
25.解:设旗杆在离底部x米的位置断裂,在给定图形上标上字母如图所示.
∵AB=x米,AB+AC=16米,
∴AC=(16﹣x)米.
在Rt△ABC中,AB=x米,AC=(16﹣x)米,BC=8米,
∴AC2=AB2+BC2,即(16﹣x)2=x2+82,
解得:x=6.
故旗杆在离底部6米的位置断裂.
一.选择题(共10小题,满分30分)
1.如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为( )
A. B.2 C. D.2
2.直角三角形的边长分别为a,b,c,且∠C=90°,若a2=9,b2=16,那么c2的值是( )
A.5 B.7 C.25 D.49
3.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
4.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8.点P是边AC上一动点,过点P作PQ∥AB交BC于点Q,D为线段PQ的中点,当BD平分∠ABC时,AP的长度为( )
A. B. C. D.
5.由下列线段为边组成的三角形是直角三角形的是( )
A.1,2,3 B.2,, C.8,24,25 D.9,12,15
6.如图,根据下列条件,能判断△ABC是直角三角形的是( )
A.AB=32,BC=42,AC=52 B.(AB﹣BC)(AB+BC)=AC
C.AB=1,BC=,AC= D.∠B=3∠A,∠C=8∠A
7.下列几组数中的勾股数是( )
A.0.3,0.5,0.4 B.﹣3,4,5
C.6,8,12 D.24,7,25
8.如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的角平分线,则三角形ADC的面积为( )
A.3 B.10 C.12 D.15
9.如图,在灯塔O的东北方向8海里处有一轮船A,在灯塔的东南方向6海里处有一渔船B,则AB间的距离为( )
A.9海里 B.10海里 C.11海里 D.12海里
10.如图,圆柱的高为4cm,底面周长为6cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知长方形ADBC的边AD、BC恰好是上、下底面的直径,则蚂蚁要吃到食物,至少要爬行( )
A.4cm B.5cm C.7cm D.10cm
二.填空题(共6小题,满分30分)
11.如图,已知在Rt△ABC中,∠ACB=90°,分别以AC,BC,AB为直径作半圆,面积分别记为S1,S2,S3,若S3=9π,则S1+S2等于 .
12.在△ABC中,AB=AC=5cm,BC=8cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的方向运动.设运动时间为t,如果过D、P两点的直线将△ABC的面积分成两个部分,使其中一部分是另一部分的2倍,那么t= 秒.
13.把图1中长和宽分别6和4的两个全等矩形沿对角线分成四个全等的直角三角形,将这四个全等的直角三角形拼成图2的正方形,则图2中小正方形ABCD的面积为 .
14.以直角三角形的三边分别向外作正方形,正方形A,B的面积分别是8cm2,10cm2,则正方形C的面积是 cm2.
15.如图,在5×2的正方形网格中,点A,P,B为格点,则∠APB= .
16.如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD= 度.
三.解答题(共9小题,满分60分)
17.如图,在△ABC中,AB=6,BC=8,AC=10.
(1)求证:△ABC是直角三角形;
(2)若AD平分∠BAC,求AD的长.
18.如图是由边长为1的小正方形拼成的网格.
(1)在图1网格中找格点P,使得AP与AB垂直.
(2)在图2网格中找格点P,使得△ABP的面积是3.
(3)在图3网格中找格点P,使得PA=PB.
19.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若AC=b,BC=a,请你利用这个图形解决下列问题:
(1)试说明a2+b2=c2;
(2)如果大正方形的面积是6,小正方形的面积是2,求(a+b)2的值.
20.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是近直角三角形,∠B>90°,∠C=50°,则∠A= .
(2)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,若CD是∠ACB的平分线.
①求证:△BDC为近直角三角形.
②求BD的长.
21.如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
22.如图,在四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.
(1)求∠ADC的度数;
(2)求出四边形ABCD的面积.
23.阅读下面材料:
勾股定理的逆定理:如果是直角三角形的三条边长a,b,c,满足a2+b2=c2,那么这个三角形是直角三角形.
能够成为直角三角形三条边长的正整数,称为勾股数.例如:32+42=52,3、4、5是一组勾股数.
古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2﹣1,c=m2+1,那么a,b,c为勾股数,你认为正确吗?如果正确,请说明理由,并利用这个结论得出一组勾股数.
24.如图,从电线杆离地面3米处向地面拉一条长为5米的拉线,这条拉线在地面的固定点距离电线杆底部有多少米?
25.如图,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,你能求出旗杆在离底部多少米的位置断裂吗?
参考答案
一.选择题(共10小题,满分30分)
1.解:在Rt△ACD中,∠A=45°,CD=1,
则AD=CD=1,
在Rt△CDB中,∠B=30°,CD=1,
则BD=,
故AB=AD+BD=+1.
故选:C.
2.解:∵∠C=90°,a2=9,b2=16,
∴c2=a2+b2=9+16=25.
故选:C.
3.解:由题意可知:中间小正方形的边长为:a﹣b,
∵每一个直角三角形的面积为:ab=×8=4,
∴4×ab+(a﹣b)2=25,
∴(a﹣b)2=25﹣16=9,
∴a﹣b=3,
故选:D.
4.解:设BQ=x,
在Rt△ABC中,∠C=90°,AB=10,BC=8,
由勾股定理得:AC===6,
∵BD平分∠ABC,
∴∠QBD=∠ABD,
∵PQ∥AB,
∴∠QDB=∠ABD,
∴∠QBD=∠QDB,
∴QD=BQ=x,
∵D为线段PQ的中点,
∴QP=2QD=2x,
∵PQ∥AB,
∴△CPQ∽△CAB,
∴==,即==,
解得:x=,CP=,
∴AP=CA﹣CP=,
故选:B.
5.解:12+22≠32,故选项A不符合题意;
22+()2≠()2,故选项B不符合题意;
82+242≠252,故选项C不符合题意;
92+122=152,故选项D符合题意;
故选:D.
6.解:A.∵AB=32=9,BC=42=16,AC=52=25,
∴AB2+BC2=92+162=337,AC2=252=625,
∴AB2+BC2≠AC2,
即△ABC不是直角三角形,故本选项不符合题意;
B.∵(AB﹣BC)(AB+BC)=AC,
∴AB2﹣BC2=AC,
即△ABC不是直角三角形,故本选项不符合题意;
C.∵AB=1,BC=,AC=,
∴AB2+BC2=12+()2=1+=,AC2=()2=,
∴AB2+BC2=AC2,
即△ABC是直角三角形,故本选项符合题意;
D.∵∠B=3∠A,∠C=8∠A,
又∵∠A+∠B+∠C=180°,
∴12∠A=180°,
∴∠A=15°,
∴最大角∠C=8∠A=120°>90°,
即△ABC不是直角三角形,故本选项不符合题意;
故选:C.
7.解:A、不是正整数,不是勾股数,不符合题意;
B、(﹣3)2+42=52,但不是正整数,不是勾股数,不符合题意;
C、62+82≠122,不是勾股数,不符合题意;
D、72+242=252,是勾股数,符合题意.
故选:D.
8.解:作DH⊥AC于H,如图,
在Rt△ABC中,∠B=90°,AB=6,BC=8,
∴AC==10,
∵AD为∠BAC的角平分线,
∴DB=DH,
∵×AB×CD=DH×AC,
∴6(8﹣DH)=10DH,解得DH=3,
∴S△ADC=×10×3=15.
故选:D.
9.解:已知东北方向和东南方向刚好是一直角,
∴∠AOB=90°,
又∵OA=8海里,OB=6海里,
∴AB==10(海里).
故选:B.
10.解:如图,将圆柱体沿着AC直线剪开,得到矩形,
则AB的长度为所求的最短距离,
根据题意圆柱的高为4cm,底面周长为6cm,
∴AC=4cm,BC=3cm,
根据勾股定理得:AB==5(cm),
∴蚂蚁要吃到食物,至少要爬行5cm,
故选:B.
二.填空题(共6小题,满分30分)
11.解:∵∠ACB=90°,
∴AC2+BC2=AB2,
∵S1=π()2×,S2=π()2×,S3=π()2×,
∴S1+S2=π()2×+π()2×=π()2×=S3,
∵S3=9π,
∴S1+S2=9π,
故答案为:9π.
12.解:分两种情况:
(1)P点在AB上时,如图1,过A作AD⊥BC于D,过P作PH⊥BC于H,
BP=t,
∵AB=AC=5cm,BC=8cm,D为BC的中点,
∴BD=BC=4,
∴AD===3,
设△BPD高为h,由2S△BPD=S△PDC,
2××4×h=×8×3﹣×4×h,
解得:h=2,
又∵∠PHB=∠ADB=90°,∠PBH=∠ABD,
∴t=(s);
(2)P点在AC上时,如图2,过A作AD⊥BC于D,过P作PH⊥BC于H,
同理可得h′=2,
∴CP=,
则t=5+5﹣=(s),
故答案为:或.
13.解:6﹣4=2,
2×2=4.
故图2中小正方形ABCD的面积为4.
故答案为:4.
14.解:根据题意得:SA+SB=SC,
∵正方形A,B的面积分别是8cm2,10cm2,
∴SC=8+10=18(cm2),
故答案为:18.
15.解:如图,延长AP交网格于点C,连接BC.
∵PC==,BC==,PB==,
∴PC=BC,PC2+BC2=PB2,
∴△PBC是等腰直角三角形,
∴∠BPC=45°,
∴∠APB=180°﹣∠BPC=135°.
故答案为:135°.
16.解:∵∠A=90°,AC=AB=4,
∴∠ACB=∠ABC=45°,
在Rt△ABC中,BC==4,
CD2+BC2=22+(4)2=36,BD2=62=36,
∴CD2+BC2=BD2,
∴∠BCD=90°,
∴∠ACD=45°,
故答案为:45.
三.解答题(共9小题,满分60分)
17.(1)证明:∵AB2+BC2=62+82=102=AC2,
∴∠B=90°,
∴△ABC是直角三角形;
(2)解:过D作DE⊥AC于E.
∵AD平分∠BAC,∠B=90°,
∴BD=DE,
在Rt△ABD中,AB=,
同理AE=,
∴AE=AB=6,
∴EC=AC﹣AE=4,
设BD=x,则DE=BD=x,CD=8﹣x,
∴x2+42=(8﹣x)2,
解得x=3,
∴AD===3.
18.解:(1)如图1,AP⊥AB.
(2)如图2,△ABP的面积==3.
∴格点P使得△ABP的面积是3(答案不唯一).
(3)如图3,∵PA==,PB==,
∴格点P使得PA=PB(答案不唯一).
19.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2.;
(2)由图可知,(b﹣a)2=2,4×ab=6﹣2=4,∴ab=2,
∴(a+b)2=(b﹣a)2+4ab=10.
20.解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为:20°;
(2)①如图1,设∠ACD=∠DCB=β,∠B=α,
则α+2β=90°,故△BDC是“近直角三角形”;
②如图2,过点D作DM⊥BC于点M,
∵CD平分∠ACB,DM⊥BC,DA⊥CA,
∴AD=DM.
在Rt△ACD和Rt△MCD中,
,
∴Rt△ACD≌Rt△MCD(HL).
∴AC=CM=4.
∵AB=3,AC=4,
∴BC===5.
∴BM=1.
设AD=DM=x,
∵DM2+BM2=DB2,
∴x2+12=(3﹣x)2,
∴x=,
∴BD=AB﹣AD=3﹣=.
21.解:连接BD,
在Rt△BAD中,
∵AB=AD=2,
∴∠ADB=45°,BD==2,
在△BCD中,
DB2+CD2=(2)2+12=9=CB2,
∴△BCD是直角三角形,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=45°+90°=135°.
22.解:(1)连接AC,在Rt△ABC中,∠ABC=90°,
∵AB=20cm,BC=15cm,
∴由勾股定理可得:AC===25(cm);
∵在△ADC中,CD=7cm,AD=24cm,
∴CD2+AD2=AC2,
∴∠ADC=90°;
(2)由(1)知,∠ADC=90°,
∴四边形ABCD的面积=S△ABC+S△ACD=+=234(cm2).
23.解:正确.理由:
∵m表示大于1的整数,
∴a,b,c都是正整数,且c是最大边,
∵(2m)2+(m2﹣1)2=(m2+1)2,
∴a2+b2=c2,
即a、b、c为勾股数.
当m=2时,可得一组勾股数3,4,5.
24.解:在Rt△ABC中,BC=3,AB=5,
由勾股定理,得AC2=AB2﹣BC2=52﹣32=42,
所以AC=4(米).
所以地面拉线固定点A到电线杆底部的距离为4米.
25.解:设旗杆在离底部x米的位置断裂,在给定图形上标上字母如图所示.
∵AB=x米,AB+AC=16米,
∴AC=(16﹣x)米.
在Rt△ABC中,AB=x米,AC=(16﹣x)米,BC=8米,
∴AC2=AB2+BC2,即(16﹣x)2=x2+82,
解得:x=6.
故旗杆在离底部6米的位置断裂.
