2021-2022学年华东师大版九年级数学下册《第26章二次函数》单元综合练习 (Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册《第26章二次函数》单元综合练习 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 341.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 11:20:43 | ||
图片预览




文档简介
2021-2022学年华师大版九年级数学下册《第26章二次函数》单元综合练习(附答案)
1.当函数y=(a﹣1)x2+bx+c是二次函数时,a的取值为( )
A.a=1 B.a=﹣1 C.a≠﹣1 D.a≠1
2.下列函数属于二次函数的是( )
A.y=x﹣ B.y=(x﹣3)2﹣x2
C.y=﹣x D.y=2(x+1)2﹣1
3.抛物线y=ax2+bx+c与直线y=ax+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
4.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A.abc>0 B.a+b+c=0 C.4a﹣2b+c<0 D.b2﹣4ac<0
5.在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如表:
x ﹣3 ﹣2 ﹣1 1 2 3 4 5
y ﹣14 ﹣7 ﹣2 2 m n ﹣7 ﹣14
则m、n的大小关系为( )
A.m>n B.m<n C.m=n D.无法确定
6.如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
A.点B坐标为(5,4) B.AB=AD
C.a=﹣ D.OC OD=16
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中,正确的是( )
A.a<0 B.b>0 C.c>﹣1 D.4a+c>2b
8.已知某二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,下列结论中正确的有( )
①abc<0;②a﹣b+c<0;③a=﹣;④8a+c>0.
A.1个 B.2个 C.3个 D.4个
9.已知二次函数y=x2+bx+c图象上部分点的坐标(x,y)的对应值如表所示:
x … 0 1 2 …
y … ﹣3 ﹣4 ﹣3 …
则b的值为( )
A.2 B. C.﹣ D.﹣2
10.已知抛物线y=ax2﹣2ax+b(a>0)的图象上三个点的坐标分别为A(﹣1,y1),B(2,y2),C(4,y3),则y1,y2,y3的大小关系为( )
A.y3>y1>y2 B.y3>y2>y1 C.y2>y1>y3 D.y2>y3>y1
11.将抛物线y=x(x+2)向左平移1个单位后的解析式为( )
A.y=x(x+1) B.y=x(x+3)
C.y=(x﹣1)(x+1) D.y=(x+1)(x+3)
12.将抛物线y=(x+2)2﹣5向右平移2个单位,再向上平移5个单位,平移后所得抛物线解析式为( )
A.y=(x+4)2 B.y=x2
C.y=x2﹣10 D.y=(x+4)2﹣10
13.二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是( )
A.向左平移2个单位,向下平移2个单位
B.向左平移1个单位,向上平移2个单位
C.向右平移1个单位,向下平移1个单位
D.向右平移2个单位,向上平移1个单位
14.将抛物线y=(x﹣2)(x﹣4)先绕坐标原点O旋转180°,再向右平移2个单位长度,所得抛物线的解析式为( )
A.y=x2+10x+24 B.y=﹣x2﹣10x﹣24
C.y=﹣x2﹣2x D.y=x2+2x
15.二次函数y=﹣x2+4x+1有( )
A.最大值5 B.最小值5 C.最大值﹣3 D.最小值﹣3
16.将二次函数y=x2+4x﹣1用配方法化成y=(x﹣h)2+k的形式,下列所配方的结果中正确的是( )
A.y=(x﹣2)2+5 B.y=(x+2)2﹣5 C.y=(x﹣4)2﹣1 D.y=(x+4)2﹣5
17.若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )
A.x1=﹣7,x2=3 B.x1=﹣6,x2=4 C.x1=6,x2=﹣4 D.x1=7,x2=﹣3
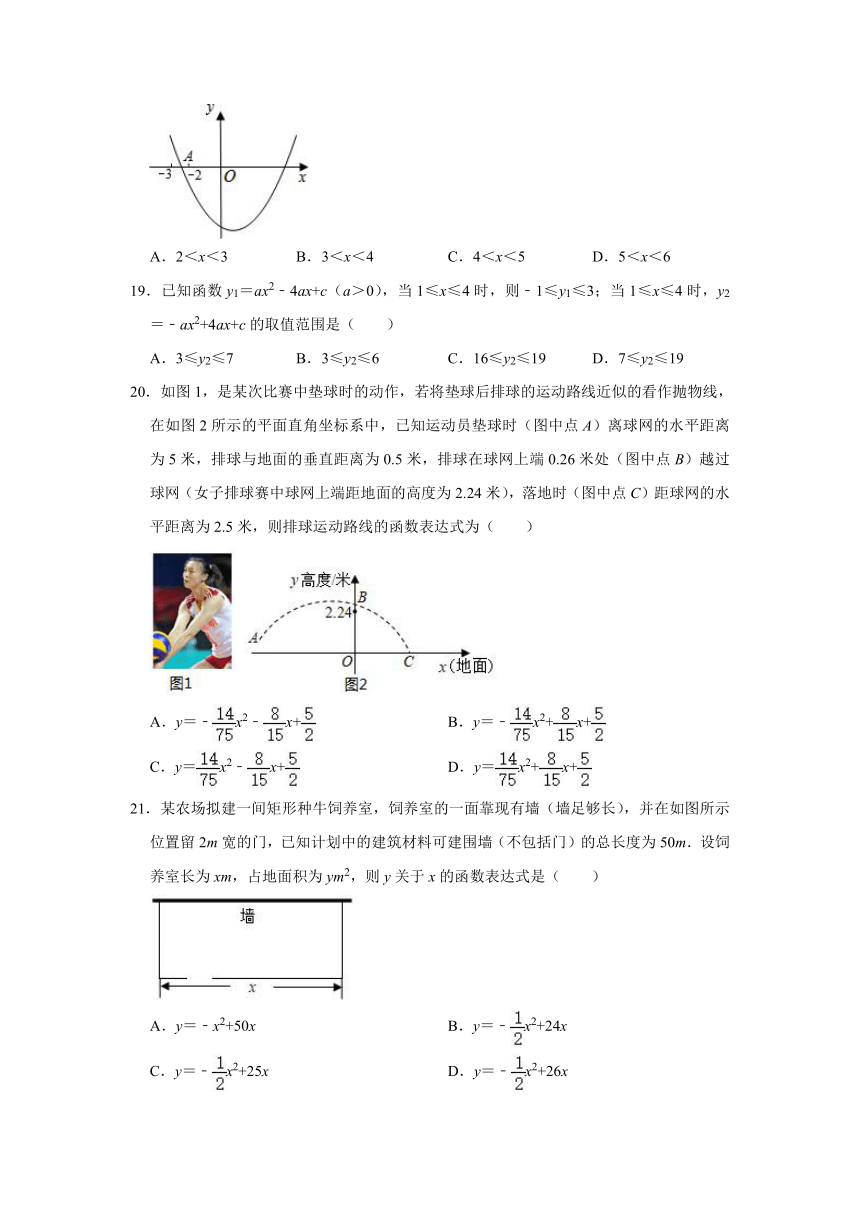
18.如图,以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
19.已知函数y1=ax2﹣4ax+c(a>0),当1≤x≤4时,则﹣1≤y1≤3;当1≤x≤4时,y2=﹣ax2+4ax+c的取值范围是( )
A.3≤y2≤7 B.3≤y2≤6 C.16≤y2≤19 D.7≤y2≤19
20.如图1,是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作抛物线,在如图2所示的平面直角坐标系中,已知运动员垫球时(图中点A)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点B)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点C)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
A.y=﹣x2﹣x+ B.y=﹣x2+x+
C.y=x2﹣x+ D.y=x2+x+
21.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门,已知计划中的建筑材料可建围墙(不包括门)的总长度为50m.设饲养室长为xm,占地面积为ym2,则y关于x的函数表达式是( )
A.y=﹣x2+50x B.y=﹣x2+24x
C.y=﹣x2+25x D.y=﹣x2+26x
22.已知x2﹣3x+y﹣5=0,则y﹣x的最大值为 .
23.二次函数y=x2﹣2x+1在3≤x≤5范围内的最小值为 .
24.如图,抛物线y=ax2+bx+3过A(﹣2,0)、B (6,0)两点,交y轴于点C,对称轴交x轴于点E,点D是其顶点,点H为x轴上一动点,连接CD、CH、DH.
(1)求抛物线的函数表达式;
(2)当点H与点B重合时,求△CDH的面积;
(3)当DH⊥CD时,求点H的坐标.
25.如图,已知抛物线y=﹣x2+bx+c经过点A(3,1)与点B(0,4).
(1)求该抛物线的解析式及顶点坐标;
(2)在第三象限内的抛物线上有一点P,使得PA⊥AB,求点P的坐标;
(3)若点C(m,n)在该抛物线上,当q≤m≤3时,1≤n≤5,请确定q的取值范围.
26.母亲节前夕,某花店准备采购一批康乃馨和萱草花,已知购买2束康乃馨和1束萱草花共需46元;购买3束康乃馨和4束萱草花共需94元.
(1)求康乃馨和萱草花的单价分别为多少元;
(2)经协商,购买康乃馨超过30束时,每增加1束,单价降低0.2元;当超过50束时,均按购买50束时的单价购进.萱草花一律按原价购买.
①购买康乃馨50束时,康乃馨的单价为 元;购买康乃馨m(30<m<50)束时,康乃馨的单价为 元(用含m的代数式表示);
②该花店计划购进康乃馨和萱草花共100束.其中康乃馨超过30束,且不超过60束.当购买康乃馨多少束时.购买两种花的总金额最少,最少为多少元?
27.空地上有一段长为am的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为120m.
(1)已知a=30,矩形菜园的一边靠墙,另三边一共用了120m木栏,且围成的矩形菜园面积为1000m2.如图1,求所利用旧墙AD的长;
(2)已知0<a<60,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
28.某公共汽车线路每天运营毛利润y(万元)与乘客量x(万人)成一次函数关系,其图象如图所示,目前通过监测发现每天平均乘客量为0.6万人次,由于运营成本较高,这条线路处于亏损状态.(毛利润=票价总收入﹣运营成本)
(1)求该线路公共汽车的单程票价和每天运营成本分别为多少元.
(2)公交公司为了扭亏,若要使每天运营毛利润在0.2~0.4万元之间(包括0.2和0.4),求平均每天的乘客量x的范围.
(3)据实际情况,发现该线路乘客量稳定,公交公司决定适当提高票价,当单程票价每提高1元时,每天平均乘客量相应减少0.05万人次,设这条线路的单程票价提高a元(1≤a≤2).当a为何值时,该线路每天运营总利润最大,并求出最大的总利润.
29.如图,抛物线C1的图象与x轴交A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3),点D为抛物线的顶点.
(1)求抛物线C1的表达式及点D坐标;
(2)将抛物线C1关于点B对称后的抛物线记为C2,抛物线C2顶点为E,求抛物线C2的表达式及点E坐标;
(3)是否在抛物线C2上存在一点P,在x轴上存在一点Q,使得以D、E、P、Q为顶点的四边形是平行四边形?若存在请求出点P的坐标,若不存在请说明理由.
参考答案
1.解:由题意得:a﹣1≠0,
解得:a≠1,
故选:D.
2.解:
A.自变量x的次数不是2,故A错误;
B.y=(x﹣3)2﹣x2整理后得到y=﹣6x+9,是一次函数,故B错误
C.由可知,自变量x的次数不是2,故C错误;
D.y=2(x+1)2﹣1是二次函数的顶点式解析式,故D正确.
故选:D.
3.解:A、一次函数y=ax+c与y轴交点应为(0,c),二次函数y=ax2+bx+c与y轴交点也应为(0,c),图象不符合,故本选项错误;
B、由抛物线可知,a>0,由直线可知,a<0,a的取值矛盾,故本选项错误;
C、由抛物线可知,a<0,由直线可知,a>0,a的取值矛盾,故本选项错误;
D、由抛物线可知,a<0,由直线可知,a<0,且抛物线与直线与y轴的交点相同,故本选项正确.
故选:D.
4.解:由图象可得,
a>0,b<0,c<0,
∴abc>0,故选项A正确;
当x=1时,y=a+b+c<0,故选项B错误;
当x=﹣2时,y=4a﹣2b+c>0,故选项C错误;
该函数图象与x轴两个交点,则b2﹣4ac>0,故选项D错误;
故选:A.
5.解:把x=1,y=2和x=﹣1,y=﹣2都代入y=﹣x2+bx+c中,得
解得,,
∴二次函数的解析式为:y=﹣x2+2x+1,
把x=2,y=m和x=3,y=n代入y=﹣x2+2x+1得,
m=﹣4+4+1=1,
n=﹣9+6+1=﹣2,
∴m>n,
故选:A.
6.解:∵抛物线y=ax2+bx+4交y轴于点A,
∴A(0,4),
∵对称轴为直线x=,AB∥x轴,
∴B(5,4).
故A无误;
如图,过点B作BE⊥x轴于点E,
则BE=4,AB=5,
∵AB∥x轴,
∴∠BAC=∠ACO,
∵点B关于直线AC的对称点恰好落在线段OC上,
∴∠ACO=∠ACB,
∴∠BAC=∠ACB,
∴BC=AB=5,
∴在Rt△BCE中,由勾股定理得:EC=3,
∴C(8,0),
∵对称轴为直线x=,
∴D(﹣3,0)
∵在Rt△ADO中,OA=4,OD=3,
∴AD=5,
∴AB=AD,
故B无误;
设y=ax2+bx+4=a(x+3)(x﹣8),
将A(0,4)代入得:4=a(0+3)(0﹣8),
∴a=﹣,
故C无误;
∵OC=8,OD=3,
∴OC OD=24,
故D错误.
综上,错误的只有D.
故选:D.
7.解:∵抛物线开口向上,
∴a>0,所以A选项错误;
∵抛物线的对称轴在y轴右侧,
∴a、b异号,
∴b<0,所以B选项错误;
∵抛物线与y轴的交点坐标为(0,c),
∴c<﹣1,所以C选项错误;
∵x=﹣2时,y>0,
∴4a﹣2b+c>0,
即4a+c>2b,所以D选项正确.
故选:D.
8.解:①函数的对称轴在y轴右侧,则ab<0,而c<0,则abc>0,故①错误,不符合题意;
②函数的对称轴为x=1,函数和x轴的一个交点是(3,0),则另外一个交点为(﹣1,0),
当x=﹣1时,y=a﹣b+c=0,故②错误,不符合题意;
③函数的对称轴为x=1=﹣,即b=﹣2a,故③正确,符合题意;
④由②③得,b=﹣2a,a﹣b+c=0,故3a+c=0,而a>0,即5a>0,故8a+c>0正确,符合题意;
故选:B.
9.解:由题意可得二次函数的顶点坐标为(1,﹣4),
∴二次函数的解析式为:y=(x﹣1)2﹣4,即y=x2﹣2x﹣3,
∴b=﹣2,
故选:D.
10.解:y=ax2﹣2ax+b(a>0),
对称轴是直线x=﹣=1,
即二次函数的开口向上,对称轴是直线x=1,
即在对称轴的右侧y随x的增大而增大,
A点关于直线x=1的对称点是D(3,y1),
∵2<3<4,
∴y3>y1>y2,
故选:A.
11.解:∵y=x(x+2)=x2+2x=(x+1)2﹣1,
∴抛物线y=x(x+2)的顶点坐标为(﹣1,﹣1),点(﹣1,﹣1)向左平移1个单位后对应点的坐标为(﹣2,﹣1),所以平移后抛物线的解析式为y=(x+2)2﹣1,即y=(x+1)(x+3).
故选:D.
12.解:将抛物线y=(x+2)2﹣5向右平移2个单位,再向上平移5个单位,平移后所得抛物线解析式为y=(x+2﹣2)2﹣5+5,即y=x2,
故选:B.
13.解:A、平移后的解析式为y=(x+2)2﹣2,当x=2时,y=14,本选项不符合题意.
B、平移后的解析式为y=(x+1)2+2,当x=2时,y=11,本选项不符合题意.
C、平移后的解析式为y=(x﹣1)2﹣1,当x=2时,y=0,函数图象经过(2,0),本选项符合题意.
D、平移后的解析式为y=(x﹣2)2+1,当x=2时,y=1,本选项不符合题意.
故选:C.
14.解:y=(x﹣2)(x﹣4)=(x﹣3)2﹣1.此时,该抛物线顶点坐标是(3,﹣1).
将该抛物线绕坐标原点O旋转180°后的顶点坐标是(﹣3,1).再向右平移2个单位长度后的顶点坐标是(﹣1,1).
所以此时抛物线的解析式为:y=﹣(x+1)2+1=﹣x2﹣2x.
故选:C.
15.解:y=﹣x2+4x+1=﹣(x﹣2)2+5.
由于a=﹣1<0,
所以该抛物线的开口方向向下,且顶点坐标是(2,5).
所以该抛物线有最大值,且最大值是5.
故选:A.
16.解:y=x2+4x﹣1=x2+4x+4﹣4﹣1=(x+2)2﹣5,
故选:B.
17.解:函数的对称轴为x=﹣=﹣=2,
而两个交点之间的距离为10,
则两个交点的坐标分别为:(7,0)、(﹣3,0),
故选:D.
18.解:∵二次函数y=ax2+bx+c的顶点为(1,﹣4),
∴对称轴为x=1,
而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3<x<﹣2,
∴右侧交点横坐标的取值范围是4<x<5.
故选:C.
19.解:∵y1=ax2﹣4ax+c=a(x﹣2)2﹣4a+c,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,c﹣4a),
∵当1≤x≤4时,则﹣1≤y1≤3,
∴c﹣4a=﹣1,
当x=4时,y=16a﹣16a+c=3,
∴c=3,
∴a=1,
∵y2=﹣ax2+4ax+c
∴y2=﹣x2+4x+3=﹣(x﹣2)2+7,
∴抛物线y2的对称轴为直线x=2,
∵1≤x≤4,
∴在此范围内,当x=2时,y2取最大值为7,当x=4时,y2取最小值为﹣4+7=3,
∴3≤y2≤7.
故选:A.
20.解:方法一:
0.26+2.24=2.5=(米)
根据题意和所建立的坐标系可知,A(﹣5,),B(0,),C(,0),
设排球运动路线的函数关系式为y=ax2+bx+c,将A、B、C的坐标代入得:
,
解得,a=﹣,b=﹣,c=,
∴排球运动路线的函数关系式为y=﹣x2﹣x+,
故选:A.
方法二:排球运动路线的函数关系式为y=ax2+bx+c,由图象可知,a<0,a、b同号,即b<0,c=,故选:A.
21.解:设饲养室长为xm,占地面积为ym2,
则y关于x的函数表达式是:y=x (50+2﹣x)=﹣x2+26x.
故选:D.
22.解:∵x2﹣3x+y﹣5=0,
∴y=﹣x2+3x+5,
∴y﹣x=﹣x2+2x+5=﹣(x﹣1)2+6,
∴y﹣x的最大值为6,
故答案为6.
23.解:y=x2﹣2x+1=(x﹣1)2,
所以,该二次函数图象的对称轴是直线x=1,且在3≤x≤5范围内y随x的增大而增大,
∴当x=3时,y最小=(3﹣1)2=4.
故答案为4.
24.解:(1)抛物线y=ax2+bx+3过A(﹣2,0)、B (6,0)两点,
∴,
解得,
∴抛物线为y=﹣x2+x+3;
(2)当x=0时,y=3,
解C(0,3),
设直线BC的解析式为y=kx+c,
把B(6,0)、C(0,3)代入得,解得,
∴直线BC的解析式为y=﹣+3,
设对称轴DE交BC于点F,则F(2,2),
∵D(2,4),
∴DF=2,
∴S△CDH==6;
(3)如图,过D作DM⊥y轴于M,过H点作HN⊥DM于N,则∠CMD=∠DNH=90°,
∵DH⊥CD,
∴∠MCD+∠MDC=∠MDC+∠NDH=90°,
∴∠MCD=∠NDH,
∴△DCM∽△HDN,
∴,
∵D(2,4),C(0,3),
∴DM=2,MC=1,HN=4,
∴,解得DN=2,
∴OH=MN=4,
∴H(4,0).
25.解:(1)将A(3,1),B(0,4)代入y=﹣x2+bx+c得,
解得,
∴所求的抛物线的解析式为:y=﹣x2+2x+4,
∵y=﹣x2+2x+4=﹣(x﹣1)2+5
∴顶点坐标为(1,5);
(2)如图,分别过点B与点P作x轴的平行线BD、PE,过点A作x轴的垂线交BD于D、交PE于点E,
∵PA⊥AB,
∴∠PAB=90°,
∴∠DAB+∠PAE=90°,
由A(3,1)、B(0,4)知BD=AD=3,
∴∠DAB=45°,
∴∠PAE=90°﹣∠DAB=90°﹣45°=45°,
∴∠PAE=∠APE=45°,
∴AE=PE,
设点P的坐标为(m,﹣m2+2m+4),则AE=,PE=xA﹣xE=3﹣m
∴m2﹣2m﹣3=3﹣m
解得:m=﹣2或m=3(点P在第三象限,不合题意,舍去),
∴m=﹣2时,﹣m2+2m+4=﹣(﹣2)2+2×(﹣2)+4=﹣4
∴点P的坐标为(﹣2,﹣4);
(3)∵1≤n≤5且抛物线的顶点为(1,5),
∴区间包含顶点,
∴q的最大值为1,
在y=﹣x2+2x+4中,当y=1时,x=﹣1或者x=3,
∴q的最小值为﹣1,
∴q的取值范围是:﹣1≤q≤1.
26.解:(1)设康乃馨和萱草花的单价分别为x元,y元,
,
解得,,
答:康乃馨和萱草花的单价分别为18元,10元;
(2)①由题意可得,
购买康乃馨50束时,康乃馨的单价为:18﹣(50﹣30)×0.2=14(元),
购买康乃馨m(30<m<50)束时,康乃馨的单价为:18﹣0.2(m﹣30)=(﹣0.2m+24)(元),
故答案为:14,(﹣0.2m+24);
②设购买康乃馨的数量为a束,购买康乃馨和萱草花的总金额为w元,
当30<a≤50时,w=a(﹣0.2a+24)+10(100﹣a)=﹣0.2(a﹣35)2+1245.
∴当a=50时,w取得最小值,此时w=1200,
当50<a≤60时,w=14a+10(100﹣a)=4a+1000,
此时,1200<4a+1000≤1240,
综上所述,当30<a≤60时,w的最小值为1200,
答:当购买康乃馨50束时,购买两种花的总金额最少,最少为1200元.
27.解:(1)设AD=x米,则AB=,
依题意得,=1000,
解得x1=100,x2=20,
∵a=30,且x≤a,
∴x=100舍去,
∴利用旧墙AD的长为20米;
(2)设AD=x米,矩形ABCD的面积为S平方米,
①如果按图1案围成矩形菜园,依题意得,
S=(0<x<a),
∵0<a<60,
∴x<a<60时,S随x的增大而增大,
当x=a时,S最大=60a﹣,
②如按图2方案围成矩形菜园,依题意得,
S=(a≤x<),
当a<<时,即0<a<40时,
则x=时,S最大=
当≤a,即40≤a<60时,S随x的增大而减小,
∴x=a时,S最大=,
综合①②,当0<a<40时,
=>0,
此时,按图2方案围成矩形菜园面积最大,最大面积为平方米,
当40≤a<60时,两种方案围成的矩形菜园面积最大值相等.
∴当0<a<40时,围成长和宽均为米的矩形菜园面积最大,最大面积为平方米;
当40≤a<60时,围成长为a米,宽为米的矩形菜园面积最大,最大面积为(60﹣)平方米.
28.解:(1)由图象可得:单程票价为1.6÷0.8=2(元/人),每天的运营成本为1.6万元;
(2)设图象的函数表达式为:y=kx+b,将(0,﹣1.6)、(0.8,0)代入上式并解得:k=2,b=1.6,
故y=2x﹣1.6,
∵k=2>0,故y随x的增大而增大,当y=0.2时,x=0.9,当y=0.4时,x=1,
∴0.9≤x≤1;
(3)设总利润为w(万元),则w=(2+a)(0.6﹣0.05a)﹣1.6=﹣0.05a2+0.5a﹣0.4,
当a=﹣=5时,
此时,a不在1≤a≤2内,当a=2时,w有最大值为0.4万元;
故当a=2时,线路每天运营总利润最大,最大的总利润为0.4万元.
29.解:(1)由题意可以假设抛物线C1的解析式为y=a(x+3)(x﹣1),
把C(0,3)代入y=a(x+3)(x﹣1),得到a=﹣1,
∴抛物线C1的解析式为y=﹣x2﹣2x+3,
顶点D(﹣1,4).
(2)∵点D关于点B的对称点E(3,﹣4),
∴抛物线C2的解析式为y=(x﹣3)2﹣4,即y=x2﹣6x+5.
(3)存在.如图,由题意,抛物线C2与x轴的另一个交点K(5,0).
①当DE为平行四边形的边时,可知点P的纵坐标为8,
当y=8时,8=x2﹣6x+5,
解得x=3±2,
∴点P的横坐标为3±2.
②当DE为对角线时,Q′与A重合,P′与K重合,
此时P′(5,0),
综上所述,满足条件的点P的坐标为(3+2,8)或(3﹣2,8)或(5,0).
1.当函数y=(a﹣1)x2+bx+c是二次函数时,a的取值为( )
A.a=1 B.a=﹣1 C.a≠﹣1 D.a≠1
2.下列函数属于二次函数的是( )
A.y=x﹣ B.y=(x﹣3)2﹣x2
C.y=﹣x D.y=2(x+1)2﹣1
3.抛物线y=ax2+bx+c与直线y=ax+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
4.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A.abc>0 B.a+b+c=0 C.4a﹣2b+c<0 D.b2﹣4ac<0
5.在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如表:
x ﹣3 ﹣2 ﹣1 1 2 3 4 5
y ﹣14 ﹣7 ﹣2 2 m n ﹣7 ﹣14
则m、n的大小关系为( )
A.m>n B.m<n C.m=n D.无法确定
6.如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
A.点B坐标为(5,4) B.AB=AD
C.a=﹣ D.OC OD=16
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中,正确的是( )
A.a<0 B.b>0 C.c>﹣1 D.4a+c>2b
8.已知某二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,下列结论中正确的有( )
①abc<0;②a﹣b+c<0;③a=﹣;④8a+c>0.
A.1个 B.2个 C.3个 D.4个
9.已知二次函数y=x2+bx+c图象上部分点的坐标(x,y)的对应值如表所示:
x … 0 1 2 …
y … ﹣3 ﹣4 ﹣3 …
则b的值为( )
A.2 B. C.﹣ D.﹣2
10.已知抛物线y=ax2﹣2ax+b(a>0)的图象上三个点的坐标分别为A(﹣1,y1),B(2,y2),C(4,y3),则y1,y2,y3的大小关系为( )
A.y3>y1>y2 B.y3>y2>y1 C.y2>y1>y3 D.y2>y3>y1
11.将抛物线y=x(x+2)向左平移1个单位后的解析式为( )
A.y=x(x+1) B.y=x(x+3)
C.y=(x﹣1)(x+1) D.y=(x+1)(x+3)
12.将抛物线y=(x+2)2﹣5向右平移2个单位,再向上平移5个单位,平移后所得抛物线解析式为( )
A.y=(x+4)2 B.y=x2
C.y=x2﹣10 D.y=(x+4)2﹣10
13.二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是( )
A.向左平移2个单位,向下平移2个单位
B.向左平移1个单位,向上平移2个单位
C.向右平移1个单位,向下平移1个单位
D.向右平移2个单位,向上平移1个单位
14.将抛物线y=(x﹣2)(x﹣4)先绕坐标原点O旋转180°,再向右平移2个单位长度,所得抛物线的解析式为( )
A.y=x2+10x+24 B.y=﹣x2﹣10x﹣24
C.y=﹣x2﹣2x D.y=x2+2x
15.二次函数y=﹣x2+4x+1有( )
A.最大值5 B.最小值5 C.最大值﹣3 D.最小值﹣3
16.将二次函数y=x2+4x﹣1用配方法化成y=(x﹣h)2+k的形式,下列所配方的结果中正确的是( )
A.y=(x﹣2)2+5 B.y=(x+2)2﹣5 C.y=(x﹣4)2﹣1 D.y=(x+4)2﹣5
17.若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )
A.x1=﹣7,x2=3 B.x1=﹣6,x2=4 C.x1=6,x2=﹣4 D.x1=7,x2=﹣3
18.如图,以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
19.已知函数y1=ax2﹣4ax+c(a>0),当1≤x≤4时,则﹣1≤y1≤3;当1≤x≤4时,y2=﹣ax2+4ax+c的取值范围是( )
A.3≤y2≤7 B.3≤y2≤6 C.16≤y2≤19 D.7≤y2≤19
20.如图1,是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作抛物线,在如图2所示的平面直角坐标系中,已知运动员垫球时(图中点A)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点B)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点C)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
A.y=﹣x2﹣x+ B.y=﹣x2+x+
C.y=x2﹣x+ D.y=x2+x+
21.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门,已知计划中的建筑材料可建围墙(不包括门)的总长度为50m.设饲养室长为xm,占地面积为ym2,则y关于x的函数表达式是( )
A.y=﹣x2+50x B.y=﹣x2+24x
C.y=﹣x2+25x D.y=﹣x2+26x
22.已知x2﹣3x+y﹣5=0,则y﹣x的最大值为 .
23.二次函数y=x2﹣2x+1在3≤x≤5范围内的最小值为 .
24.如图,抛物线y=ax2+bx+3过A(﹣2,0)、B (6,0)两点,交y轴于点C,对称轴交x轴于点E,点D是其顶点,点H为x轴上一动点,连接CD、CH、DH.
(1)求抛物线的函数表达式;
(2)当点H与点B重合时,求△CDH的面积;
(3)当DH⊥CD时,求点H的坐标.
25.如图,已知抛物线y=﹣x2+bx+c经过点A(3,1)与点B(0,4).
(1)求该抛物线的解析式及顶点坐标;
(2)在第三象限内的抛物线上有一点P,使得PA⊥AB,求点P的坐标;
(3)若点C(m,n)在该抛物线上,当q≤m≤3时,1≤n≤5,请确定q的取值范围.
26.母亲节前夕,某花店准备采购一批康乃馨和萱草花,已知购买2束康乃馨和1束萱草花共需46元;购买3束康乃馨和4束萱草花共需94元.
(1)求康乃馨和萱草花的单价分别为多少元;
(2)经协商,购买康乃馨超过30束时,每增加1束,单价降低0.2元;当超过50束时,均按购买50束时的单价购进.萱草花一律按原价购买.
①购买康乃馨50束时,康乃馨的单价为 元;购买康乃馨m(30<m<50)束时,康乃馨的单价为 元(用含m的代数式表示);
②该花店计划购进康乃馨和萱草花共100束.其中康乃馨超过30束,且不超过60束.当购买康乃馨多少束时.购买两种花的总金额最少,最少为多少元?
27.空地上有一段长为am的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为120m.
(1)已知a=30,矩形菜园的一边靠墙,另三边一共用了120m木栏,且围成的矩形菜园面积为1000m2.如图1,求所利用旧墙AD的长;
(2)已知0<a<60,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
28.某公共汽车线路每天运营毛利润y(万元)与乘客量x(万人)成一次函数关系,其图象如图所示,目前通过监测发现每天平均乘客量为0.6万人次,由于运营成本较高,这条线路处于亏损状态.(毛利润=票价总收入﹣运营成本)
(1)求该线路公共汽车的单程票价和每天运营成本分别为多少元.
(2)公交公司为了扭亏,若要使每天运营毛利润在0.2~0.4万元之间(包括0.2和0.4),求平均每天的乘客量x的范围.
(3)据实际情况,发现该线路乘客量稳定,公交公司决定适当提高票价,当单程票价每提高1元时,每天平均乘客量相应减少0.05万人次,设这条线路的单程票价提高a元(1≤a≤2).当a为何值时,该线路每天运营总利润最大,并求出最大的总利润.
29.如图,抛物线C1的图象与x轴交A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3),点D为抛物线的顶点.
(1)求抛物线C1的表达式及点D坐标;
(2)将抛物线C1关于点B对称后的抛物线记为C2,抛物线C2顶点为E,求抛物线C2的表达式及点E坐标;
(3)是否在抛物线C2上存在一点P,在x轴上存在一点Q,使得以D、E、P、Q为顶点的四边形是平行四边形?若存在请求出点P的坐标,若不存在请说明理由.
参考答案
1.解:由题意得:a﹣1≠0,
解得:a≠1,
故选:D.
2.解:
A.自变量x的次数不是2,故A错误;
B.y=(x﹣3)2﹣x2整理后得到y=﹣6x+9,是一次函数,故B错误
C.由可知,自变量x的次数不是2,故C错误;
D.y=2(x+1)2﹣1是二次函数的顶点式解析式,故D正确.
故选:D.
3.解:A、一次函数y=ax+c与y轴交点应为(0,c),二次函数y=ax2+bx+c与y轴交点也应为(0,c),图象不符合,故本选项错误;
B、由抛物线可知,a>0,由直线可知,a<0,a的取值矛盾,故本选项错误;
C、由抛物线可知,a<0,由直线可知,a>0,a的取值矛盾,故本选项错误;
D、由抛物线可知,a<0,由直线可知,a<0,且抛物线与直线与y轴的交点相同,故本选项正确.
故选:D.
4.解:由图象可得,
a>0,b<0,c<0,
∴abc>0,故选项A正确;
当x=1时,y=a+b+c<0,故选项B错误;
当x=﹣2时,y=4a﹣2b+c>0,故选项C错误;
该函数图象与x轴两个交点,则b2﹣4ac>0,故选项D错误;
故选:A.
5.解:把x=1,y=2和x=﹣1,y=﹣2都代入y=﹣x2+bx+c中,得
解得,,
∴二次函数的解析式为:y=﹣x2+2x+1,
把x=2,y=m和x=3,y=n代入y=﹣x2+2x+1得,
m=﹣4+4+1=1,
n=﹣9+6+1=﹣2,
∴m>n,
故选:A.
6.解:∵抛物线y=ax2+bx+4交y轴于点A,
∴A(0,4),
∵对称轴为直线x=,AB∥x轴,
∴B(5,4).
故A无误;
如图,过点B作BE⊥x轴于点E,
则BE=4,AB=5,
∵AB∥x轴,
∴∠BAC=∠ACO,
∵点B关于直线AC的对称点恰好落在线段OC上,
∴∠ACO=∠ACB,
∴∠BAC=∠ACB,
∴BC=AB=5,
∴在Rt△BCE中,由勾股定理得:EC=3,
∴C(8,0),
∵对称轴为直线x=,
∴D(﹣3,0)
∵在Rt△ADO中,OA=4,OD=3,
∴AD=5,
∴AB=AD,
故B无误;
设y=ax2+bx+4=a(x+3)(x﹣8),
将A(0,4)代入得:4=a(0+3)(0﹣8),
∴a=﹣,
故C无误;
∵OC=8,OD=3,
∴OC OD=24,
故D错误.
综上,错误的只有D.
故选:D.
7.解:∵抛物线开口向上,
∴a>0,所以A选项错误;
∵抛物线的对称轴在y轴右侧,
∴a、b异号,
∴b<0,所以B选项错误;
∵抛物线与y轴的交点坐标为(0,c),
∴c<﹣1,所以C选项错误;
∵x=﹣2时,y>0,
∴4a﹣2b+c>0,
即4a+c>2b,所以D选项正确.
故选:D.
8.解:①函数的对称轴在y轴右侧,则ab<0,而c<0,则abc>0,故①错误,不符合题意;
②函数的对称轴为x=1,函数和x轴的一个交点是(3,0),则另外一个交点为(﹣1,0),
当x=﹣1时,y=a﹣b+c=0,故②错误,不符合题意;
③函数的对称轴为x=1=﹣,即b=﹣2a,故③正确,符合题意;
④由②③得,b=﹣2a,a﹣b+c=0,故3a+c=0,而a>0,即5a>0,故8a+c>0正确,符合题意;
故选:B.
9.解:由题意可得二次函数的顶点坐标为(1,﹣4),
∴二次函数的解析式为:y=(x﹣1)2﹣4,即y=x2﹣2x﹣3,
∴b=﹣2,
故选:D.
10.解:y=ax2﹣2ax+b(a>0),
对称轴是直线x=﹣=1,
即二次函数的开口向上,对称轴是直线x=1,
即在对称轴的右侧y随x的增大而增大,
A点关于直线x=1的对称点是D(3,y1),
∵2<3<4,
∴y3>y1>y2,
故选:A.
11.解:∵y=x(x+2)=x2+2x=(x+1)2﹣1,
∴抛物线y=x(x+2)的顶点坐标为(﹣1,﹣1),点(﹣1,﹣1)向左平移1个单位后对应点的坐标为(﹣2,﹣1),所以平移后抛物线的解析式为y=(x+2)2﹣1,即y=(x+1)(x+3).
故选:D.
12.解:将抛物线y=(x+2)2﹣5向右平移2个单位,再向上平移5个单位,平移后所得抛物线解析式为y=(x+2﹣2)2﹣5+5,即y=x2,
故选:B.
13.解:A、平移后的解析式为y=(x+2)2﹣2,当x=2时,y=14,本选项不符合题意.
B、平移后的解析式为y=(x+1)2+2,当x=2时,y=11,本选项不符合题意.
C、平移后的解析式为y=(x﹣1)2﹣1,当x=2时,y=0,函数图象经过(2,0),本选项符合题意.
D、平移后的解析式为y=(x﹣2)2+1,当x=2时,y=1,本选项不符合题意.
故选:C.
14.解:y=(x﹣2)(x﹣4)=(x﹣3)2﹣1.此时,该抛物线顶点坐标是(3,﹣1).
将该抛物线绕坐标原点O旋转180°后的顶点坐标是(﹣3,1).再向右平移2个单位长度后的顶点坐标是(﹣1,1).
所以此时抛物线的解析式为:y=﹣(x+1)2+1=﹣x2﹣2x.
故选:C.
15.解:y=﹣x2+4x+1=﹣(x﹣2)2+5.
由于a=﹣1<0,
所以该抛物线的开口方向向下,且顶点坐标是(2,5).
所以该抛物线有最大值,且最大值是5.
故选:A.
16.解:y=x2+4x﹣1=x2+4x+4﹣4﹣1=(x+2)2﹣5,
故选:B.
17.解:函数的对称轴为x=﹣=﹣=2,
而两个交点之间的距离为10,
则两个交点的坐标分别为:(7,0)、(﹣3,0),
故选:D.
18.解:∵二次函数y=ax2+bx+c的顶点为(1,﹣4),
∴对称轴为x=1,
而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3<x<﹣2,
∴右侧交点横坐标的取值范围是4<x<5.
故选:C.
19.解:∵y1=ax2﹣4ax+c=a(x﹣2)2﹣4a+c,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,c﹣4a),
∵当1≤x≤4时,则﹣1≤y1≤3,
∴c﹣4a=﹣1,
当x=4时,y=16a﹣16a+c=3,
∴c=3,
∴a=1,
∵y2=﹣ax2+4ax+c
∴y2=﹣x2+4x+3=﹣(x﹣2)2+7,
∴抛物线y2的对称轴为直线x=2,
∵1≤x≤4,
∴在此范围内,当x=2时,y2取最大值为7,当x=4时,y2取最小值为﹣4+7=3,
∴3≤y2≤7.
故选:A.
20.解:方法一:
0.26+2.24=2.5=(米)
根据题意和所建立的坐标系可知,A(﹣5,),B(0,),C(,0),
设排球运动路线的函数关系式为y=ax2+bx+c,将A、B、C的坐标代入得:
,
解得,a=﹣,b=﹣,c=,
∴排球运动路线的函数关系式为y=﹣x2﹣x+,
故选:A.
方法二:排球运动路线的函数关系式为y=ax2+bx+c,由图象可知,a<0,a、b同号,即b<0,c=,故选:A.
21.解:设饲养室长为xm,占地面积为ym2,
则y关于x的函数表达式是:y=x (50+2﹣x)=﹣x2+26x.
故选:D.
22.解:∵x2﹣3x+y﹣5=0,
∴y=﹣x2+3x+5,
∴y﹣x=﹣x2+2x+5=﹣(x﹣1)2+6,
∴y﹣x的最大值为6,
故答案为6.
23.解:y=x2﹣2x+1=(x﹣1)2,
所以,该二次函数图象的对称轴是直线x=1,且在3≤x≤5范围内y随x的增大而增大,
∴当x=3时,y最小=(3﹣1)2=4.
故答案为4.
24.解:(1)抛物线y=ax2+bx+3过A(﹣2,0)、B (6,0)两点,
∴,
解得,
∴抛物线为y=﹣x2+x+3;
(2)当x=0时,y=3,
解C(0,3),
设直线BC的解析式为y=kx+c,
把B(6,0)、C(0,3)代入得,解得,
∴直线BC的解析式为y=﹣+3,
设对称轴DE交BC于点F,则F(2,2),
∵D(2,4),
∴DF=2,
∴S△CDH==6;
(3)如图,过D作DM⊥y轴于M,过H点作HN⊥DM于N,则∠CMD=∠DNH=90°,
∵DH⊥CD,
∴∠MCD+∠MDC=∠MDC+∠NDH=90°,
∴∠MCD=∠NDH,
∴△DCM∽△HDN,
∴,
∵D(2,4),C(0,3),
∴DM=2,MC=1,HN=4,
∴,解得DN=2,
∴OH=MN=4,
∴H(4,0).
25.解:(1)将A(3,1),B(0,4)代入y=﹣x2+bx+c得,
解得,
∴所求的抛物线的解析式为:y=﹣x2+2x+4,
∵y=﹣x2+2x+4=﹣(x﹣1)2+5
∴顶点坐标为(1,5);
(2)如图,分别过点B与点P作x轴的平行线BD、PE,过点A作x轴的垂线交BD于D、交PE于点E,
∵PA⊥AB,
∴∠PAB=90°,
∴∠DAB+∠PAE=90°,
由A(3,1)、B(0,4)知BD=AD=3,
∴∠DAB=45°,
∴∠PAE=90°﹣∠DAB=90°﹣45°=45°,
∴∠PAE=∠APE=45°,
∴AE=PE,
设点P的坐标为(m,﹣m2+2m+4),则AE=,PE=xA﹣xE=3﹣m
∴m2﹣2m﹣3=3﹣m
解得:m=﹣2或m=3(点P在第三象限,不合题意,舍去),
∴m=﹣2时,﹣m2+2m+4=﹣(﹣2)2+2×(﹣2)+4=﹣4
∴点P的坐标为(﹣2,﹣4);
(3)∵1≤n≤5且抛物线的顶点为(1,5),
∴区间包含顶点,
∴q的最大值为1,
在y=﹣x2+2x+4中,当y=1时,x=﹣1或者x=3,
∴q的最小值为﹣1,
∴q的取值范围是:﹣1≤q≤1.
26.解:(1)设康乃馨和萱草花的单价分别为x元,y元,
,
解得,,
答:康乃馨和萱草花的单价分别为18元,10元;
(2)①由题意可得,
购买康乃馨50束时,康乃馨的单价为:18﹣(50﹣30)×0.2=14(元),
购买康乃馨m(30<m<50)束时,康乃馨的单价为:18﹣0.2(m﹣30)=(﹣0.2m+24)(元),
故答案为:14,(﹣0.2m+24);
②设购买康乃馨的数量为a束,购买康乃馨和萱草花的总金额为w元,
当30<a≤50时,w=a(﹣0.2a+24)+10(100﹣a)=﹣0.2(a﹣35)2+1245.
∴当a=50时,w取得最小值,此时w=1200,
当50<a≤60时,w=14a+10(100﹣a)=4a+1000,
此时,1200<4a+1000≤1240,
综上所述,当30<a≤60时,w的最小值为1200,
答:当购买康乃馨50束时,购买两种花的总金额最少,最少为1200元.
27.解:(1)设AD=x米,则AB=,
依题意得,=1000,
解得x1=100,x2=20,
∵a=30,且x≤a,
∴x=100舍去,
∴利用旧墙AD的长为20米;
(2)设AD=x米,矩形ABCD的面积为S平方米,
①如果按图1案围成矩形菜园,依题意得,
S=(0<x<a),
∵0<a<60,
∴x<a<60时,S随x的增大而增大,
当x=a时,S最大=60a﹣,
②如按图2方案围成矩形菜园,依题意得,
S=(a≤x<),
当a<<时,即0<a<40时,
则x=时,S最大=
当≤a,即40≤a<60时,S随x的增大而减小,
∴x=a时,S最大=,
综合①②,当0<a<40时,
=>0,
此时,按图2方案围成矩形菜园面积最大,最大面积为平方米,
当40≤a<60时,两种方案围成的矩形菜园面积最大值相等.
∴当0<a<40时,围成长和宽均为米的矩形菜园面积最大,最大面积为平方米;
当40≤a<60时,围成长为a米,宽为米的矩形菜园面积最大,最大面积为(60﹣)平方米.
28.解:(1)由图象可得:单程票价为1.6÷0.8=2(元/人),每天的运营成本为1.6万元;
(2)设图象的函数表达式为:y=kx+b,将(0,﹣1.6)、(0.8,0)代入上式并解得:k=2,b=1.6,
故y=2x﹣1.6,
∵k=2>0,故y随x的增大而增大,当y=0.2时,x=0.9,当y=0.4时,x=1,
∴0.9≤x≤1;
(3)设总利润为w(万元),则w=(2+a)(0.6﹣0.05a)﹣1.6=﹣0.05a2+0.5a﹣0.4,
当a=﹣=5时,
此时,a不在1≤a≤2内,当a=2时,w有最大值为0.4万元;
故当a=2时,线路每天运营总利润最大,最大的总利润为0.4万元.
29.解:(1)由题意可以假设抛物线C1的解析式为y=a(x+3)(x﹣1),
把C(0,3)代入y=a(x+3)(x﹣1),得到a=﹣1,
∴抛物线C1的解析式为y=﹣x2﹣2x+3,
顶点D(﹣1,4).
(2)∵点D关于点B的对称点E(3,﹣4),
∴抛物线C2的解析式为y=(x﹣3)2﹣4,即y=x2﹣6x+5.
(3)存在.如图,由题意,抛物线C2与x轴的另一个交点K(5,0).
①当DE为平行四边形的边时,可知点P的纵坐标为8,
当y=8时,8=x2﹣6x+5,
解得x=3±2,
∴点P的横坐标为3±2.
②当DE为对角线时,Q′与A重合,P′与K重合,
此时P′(5,0),
综上所述,满足条件的点P的坐标为(3+2,8)或(3﹣2,8)或(5,0).
