2021-2022学年鲁教版(五四制)八年级数学上册5.2平行四边形的判定 同步达标测评(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学上册5.2平行四边形的判定 同步达标测评(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 296.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 16:00:02 | ||
图片预览




文档简介
2021-2022学年鲁教版八年级数学上册《5.2平行四边形的判定》同步达标测评(附答案)
一.选择题(共10小题,满分50分)
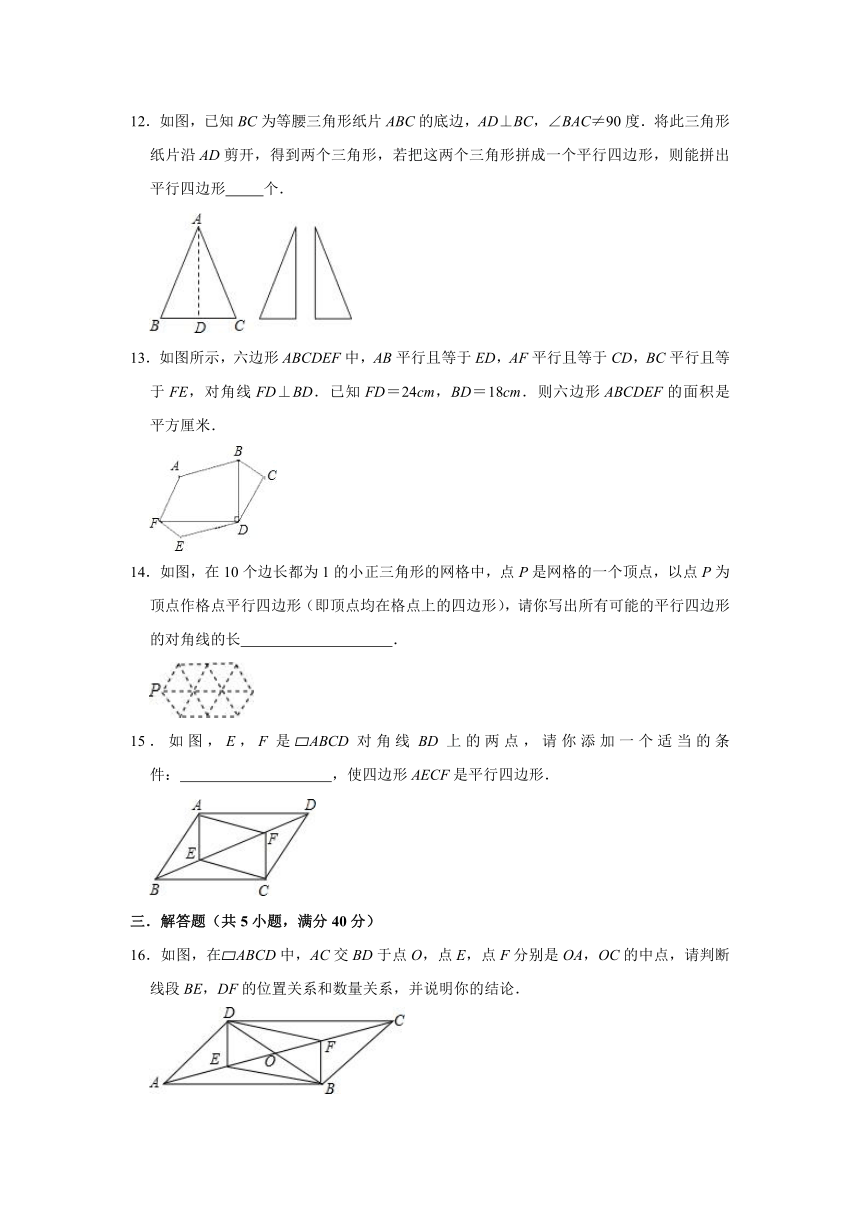
1.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
A.平行四边形 B.矩形 C.菱形 D.梯形
2.四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:
①AB∥CD,AD∥BC; ②AB=CD,AD=BC;
③AO=CO,BO=DO; ④AB∥CD,AD=BC.
其中一定能判断这个四边形是平行四边形的条件共有( )
A.1组 B.2组 C.3组 D.4组
3.已知四边形ABCD,有以下四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法种数共有( )
A.6种 B.5种 C.4种 D.3种
4.能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
5.如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为( )
A.甲<乙<丙 B.乙<丙<甲 C.丙<乙<甲 D.甲=乙=丙
6.如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD、BF为邻边作平行四边形BDEF,又APBE(点P、E在直线AB的同侧),如果BD=AB,那么△PBC的面积与△ABC面积之比为( )
A. B. C. D.
7.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,则图中的平行四边形的个数共有( )
A.12个 B.9个 C.7个 D.5个
8.如图,在 ABCD中,EF∥AB,GH∥AD,EF与GH交于点O,则该图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
9.在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是( )
A.∠BDC=∠BCD B.∠ABC=∠DAB C.∠ADB=∠DAC D.∠AOB=∠BOC
10.下列三角形纸片,能沿直线剪一刀得到等腰梯形的是( )
A. B. C. D.
二.填空题(共5小题,满分30分)
11.用两个全等的三角形(三边不等)共能拼成 个不同的平行四边形.
12.如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90度.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形,则能拼出平行四边形 个.
13.如图所示,六边形ABCDEF中,AB平行且等于ED,AF平行且等于CD,BC平行且等于FE,对角线FD⊥BD.已知FD=24cm,BD=18cm.则六边形ABCDEF的面积是 平方厘米.
14.如图,在10个边长都为1的小正三角形的网格中,点P是网格的一个顶点,以点P为顶点作格点平行四边形(即顶点均在格点上的四边形),请你写出所有可能的平行四边形的对角线的长 .
15.如图,E,F是 ABCD对角线BD上的两点,请你添加一个适当的条件: ,使四边形AECF是平行四边形.
三.解答题(共5小题,满分40分)
16.如图,在 ABCD中,AC交BD于点O,点E,点F分别是OA,OC的中点,请判断线段BE,DF的位置关系和数量关系,并说明你的结论.
17.如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
18.如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.
19.如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,AF与BG交于点E.
(1)求证:AF⊥BG,DF=CG;
(2)若AB=10,AD=6,AF=8,求FG和BG的长度.
20.在平面直角坐标系中描出下列各点A(0,4),B(﹣4,0),C(6,0),D(2,4),并将各点用线段依次连接构成一个四边形ABCD.
(1)四边形ABCD是什么特殊的四边形?
(2)在平面直角坐标系中,若PA=PB=PC=PD,则点P的坐标是 ;
(3)在四边形ABCD内是否存在一点P,使得△APB、△BPC、△CPD、△APD都是等腰三角形?若有,请求出P点的坐标;若没有,请说明理由.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,
∴AD=BC AB=CD
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
故选:A.
2.解:①根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,可知①能判断这个四边形是平行四边形;
②根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,可知②能判断这个四边形是平行四边形;
③根据平行四边形的判定定理:两条对角线互相平分的四边形是平行四边形,可知③能判断这个四边形是平行四边形;
④根据平行四边形的判定定理:一组对边平行,一组对边相等的四边形不一定是平行四边形,可知④错误;
故给出下列四组条件中,①②③能判断这个四边形是平行四边形,
故选:C.
3.解:依题意得有四种组合方式:
(1)①③,利用两组对边平行的四边形是平行四边形判定;
(2)②④,利用两组对边相等的四边形是平行四边形判定;
(3)①②或③④,利用一组对边平行且相等的四边形是平行四边形判定.
故选:C.
4.解:根据平行四边形的判定定理知,A、B、D均不符合是平行四边形的条件;
C满足两组对边分别相等的四边形是平行四边形.
故选:C.
5.解:图1中,甲走的路线长是AC+BC的长度;
延长AD和BF交于C,如图2,
∵∠DEA=∠B=60°,
∴DE∥CF,
同理EF∥CD,
∴四边形CDEF是平行四边形,
∴EF=CD,DE=CF,
即乙走的路线长是AD+DE+EF+FB=AD+CD+CF+FB=AC+BC的长;
延长AG和BK交于C,如图3,
与以上证明过程类似GH=CK,CG=HK,
即丙走的路线长是AG+GH+HK+KB=AG+CG+CK+BK=AC+BC的长;
即甲=乙=丙,
故选:D.
6.解:过点P作PH∥BC交AB于H,连接CH,PF,
∵APBE,
∴四边形APEB是平行四边形,
∴PE∥AB,PE=AB,
∵四边形BDEF是平行四边形,
∴EF∥BD,EF=BD,
即EF∥AB,
∴P,E,F共线,
设BD=a,
∵BD=AB,
∴PE=AB=4a,
则PF=PE﹣EF=3a,
∵PH∥BC,
∴S△HBC=S△PBC,
∵PF∥AB,
∴四边形BFPH是平行四边形,
∴BH=PF=3a,
∵S△HBC:S△ABC=BH:AB=3a:4a=3:4,
∴S△PBC:S△ABC=3:4.
故选:D.
7.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边AEOH,HOFD,EBNO,ONCF,AEFD,EBCF,ABNH,HNCD,ABCD都是平行四边形,共9个.
故选:B.
8.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边DEOH、DEFC、DHGA、BGOF、BGHC、BAEF、AGOE、CHOF和ABCD都是平行四边形,共9个.
故选:C.
9.解:A、∵∠BDC=∠BCD,
∴BD=BC,
根据已知AD∥BC不能推出四边形ABCD是等腰梯形,故本选项错误;
B、根据∠ABC=∠DAB和AD∥BC不能推出四边形ABCD是等腰梯形,故本选项错误;
C、∵∠ADB=∠DAC,AD∥BC,
∴∠ADB=∠DAC=∠DBC=∠ACB,
∴OA=OD,OB=OC,
∴AC=BD,
∵AD∥BC,
∴四边形ABCD是等腰梯形,故本选项正确;
D、根据∠AOB=∠BOC,只能推出AC⊥BD,
再根据AD∥BC不能推出四边形ABCD是等腰梯形,故本选项错误.
故选:C.
10.解:因为已知两角分别为50°,80°,
则另外一个角为50°,
则沿与另一边平行的直线把80°的角剪掉,
得到的是个梯形且是个等腰梯形,
因为同一底上的两底角相等.
故选:B.
二.填空题(共5小题,满分30分)
11.解:(如图)利用全等三角形的对应边相等,分别让三条边重合(作为平行四边形的对角线),就可以得到三个不同的平行四边形
12.解:若要拼成平行四边形,即是分别让它们的一组对应边重合,另外两组对应边分别平行.
故能拼出3个.
故答案为:3.
13.解:连接AC交BD于G,AE交DF于H.
∵AB平行且等于ED,AF平行且等于CD,
∴四边形AEDB是平行四边形,四边形AFDC是平行四边形,
∴AD∥BD,AC∥FD,AE=BD,AC=FD,
∵FD⊥BD,
∴四边形AHDG是矩形,
∴AH=DG,且AE⊥DF,BD⊥AC,
∴EH=BG.
∴六边形的面积=平行四边形AFDC的面积+三角形ABC的面积+三角形EFD的面积=FD BD=24×18=432.
14.解:平行四边形有:PABD,PACE,PMND,PMQE,APMD,APNE,PQGA,PMEB和PCGM.
平行四四边形PABD,平行四边形PMND对角线长是1和;
平行四边形PACE和PMQE的对角线长是:和;
平行四边形APNE和PMEB的对角线长是2和2;
平行四边形PQGA和PCGM的对角线长是3和.
故答案为:1或或或2或3.
15.解:使四边形AECF是平行四边形.就要使AE∥CF,AE=CF,就要使△AEB≌△CFD,而在平行四边形中已有AB=CD,∠ABE=∠CDF,再加一个BE=DF,或BF=DE就可用SAS证△AEB≌△CFD,BE=DF,或BF=DE.
故答案为:BE=DF或BF=DE或∠BAE=∠DCF.
三.解答题(共5小题,满分40分)
16.解:BE=DF,BE∥DF
因为ABCD是平行四边形,所以OA=OC,OB=OD,
因为E,F分别是OA,OC的中点,所以OE=OF,
所以BFDE是平行四边形,所以BE=DF,BE∥DF
17.证明:∵BE∥DF,
∴∠BEC=∠DFA,
在△ADF和△CBE中,
∴△ADF≌△CBE(AAS),
∴BE=DF,
又∵BE∥DF,
∴四边形DEBF是平行四边形.
18.证明:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形DEBF是平行四边形.
19.(1)证明:∵AF平分∠BAD,
∴∠DAF=∠BAF=∠BAD.
∵BG平分∠ABC,
∴∠ABG=∠CBG=∠ABC.
∵四边形ABCD平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴∠BAD+∠ABC=180°,
即2∠BAF+2∠ABG=180°,
∴∠BAF+∠ABG=90°.
∴∠AEB=180°﹣(∠BAF+∠ABG)=180°﹣90°=90°.
∴AF⊥BG;
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AFD=∠DAF,
∴DF=AD,
∵AB∥CD,
∴∠ABG=∠CGB,
∴∠CBG=∠CGB,
∴CG=BC,
∵AD=BC.
∴DF=CG;
(2)解:∵DF=AD=6,
∴CG=DF=6.
∴CG+DF=12,
∵四边形ABCD平行四边形,
∴CD=AB=10.
∴10+FG=12,
∴FG=2,
过点B作BH∥AF交DC的延长线于点H.
∴∠GBH=∠AEB=90°.
∵AF∥BH,AB∥FH,
∴四边形ABHF为平行四边形.
∴BH=AF=8,FH=AB=10.
∴GH=FG+FH=2+10=12,
∴在Rt△BHG中:BG==.
∴FG的长度为2,BG的长度为4.
20.解:(1)如图所示:是等腰梯形;
(2)点P一定在两底的垂直平分线上.设点P(1,y),
点P也在两腰的中垂线上:=,
解得:y=﹣1,
故P(1,﹣1);
(3)当点P不在两腰的中垂线上时,设点P(1,m),
DC=CP,
=4,
解得:m=,
故P(1,).
一.选择题(共10小题,满分50分)
1.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
A.平行四边形 B.矩形 C.菱形 D.梯形
2.四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:
①AB∥CD,AD∥BC; ②AB=CD,AD=BC;
③AO=CO,BO=DO; ④AB∥CD,AD=BC.
其中一定能判断这个四边形是平行四边形的条件共有( )
A.1组 B.2组 C.3组 D.4组
3.已知四边形ABCD,有以下四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法种数共有( )
A.6种 B.5种 C.4种 D.3种
4.能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
5.如图,图1、图2、图3分别表示甲、乙、丙三人由A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为( )
A.甲<乙<丙 B.乙<丙<甲 C.丙<乙<甲 D.甲=乙=丙
6.如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD、BF为邻边作平行四边形BDEF,又APBE(点P、E在直线AB的同侧),如果BD=AB,那么△PBC的面积与△ABC面积之比为( )
A. B. C. D.
7.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,则图中的平行四边形的个数共有( )
A.12个 B.9个 C.7个 D.5个
8.如图,在 ABCD中,EF∥AB,GH∥AD,EF与GH交于点O,则该图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
9.在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是( )
A.∠BDC=∠BCD B.∠ABC=∠DAB C.∠ADB=∠DAC D.∠AOB=∠BOC
10.下列三角形纸片,能沿直线剪一刀得到等腰梯形的是( )
A. B. C. D.
二.填空题(共5小题,满分30分)
11.用两个全等的三角形(三边不等)共能拼成 个不同的平行四边形.
12.如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90度.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形,则能拼出平行四边形 个.
13.如图所示,六边形ABCDEF中,AB平行且等于ED,AF平行且等于CD,BC平行且等于FE,对角线FD⊥BD.已知FD=24cm,BD=18cm.则六边形ABCDEF的面积是 平方厘米.
14.如图,在10个边长都为1的小正三角形的网格中,点P是网格的一个顶点,以点P为顶点作格点平行四边形(即顶点均在格点上的四边形),请你写出所有可能的平行四边形的对角线的长 .
15.如图,E,F是 ABCD对角线BD上的两点,请你添加一个适当的条件: ,使四边形AECF是平行四边形.
三.解答题(共5小题,满分40分)
16.如图,在 ABCD中,AC交BD于点O,点E,点F分别是OA,OC的中点,请判断线段BE,DF的位置关系和数量关系,并说明你的结论.
17.如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
18.如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.
19.如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,AF与BG交于点E.
(1)求证:AF⊥BG,DF=CG;
(2)若AB=10,AD=6,AF=8,求FG和BG的长度.
20.在平面直角坐标系中描出下列各点A(0,4),B(﹣4,0),C(6,0),D(2,4),并将各点用线段依次连接构成一个四边形ABCD.
(1)四边形ABCD是什么特殊的四边形?
(2)在平面直角坐标系中,若PA=PB=PC=PD,则点P的坐标是 ;
(3)在四边形ABCD内是否存在一点P,使得△APB、△BPC、△CPD、△APD都是等腰三角形?若有,请求出P点的坐标;若没有,请说明理由.
参考答案
一.选择题(共10小题,满分50分)
1.解:∵分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,
∴AD=BC AB=CD
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
故选:A.
2.解:①根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,可知①能判断这个四边形是平行四边形;
②根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,可知②能判断这个四边形是平行四边形;
③根据平行四边形的判定定理:两条对角线互相平分的四边形是平行四边形,可知③能判断这个四边形是平行四边形;
④根据平行四边形的判定定理:一组对边平行,一组对边相等的四边形不一定是平行四边形,可知④错误;
故给出下列四组条件中,①②③能判断这个四边形是平行四边形,
故选:C.
3.解:依题意得有四种组合方式:
(1)①③,利用两组对边平行的四边形是平行四边形判定;
(2)②④,利用两组对边相等的四边形是平行四边形判定;
(3)①②或③④,利用一组对边平行且相等的四边形是平行四边形判定.
故选:C.
4.解:根据平行四边形的判定定理知,A、B、D均不符合是平行四边形的条件;
C满足两组对边分别相等的四边形是平行四边形.
故选:C.
5.解:图1中,甲走的路线长是AC+BC的长度;
延长AD和BF交于C,如图2,
∵∠DEA=∠B=60°,
∴DE∥CF,
同理EF∥CD,
∴四边形CDEF是平行四边形,
∴EF=CD,DE=CF,
即乙走的路线长是AD+DE+EF+FB=AD+CD+CF+FB=AC+BC的长;
延长AG和BK交于C,如图3,
与以上证明过程类似GH=CK,CG=HK,
即丙走的路线长是AG+GH+HK+KB=AG+CG+CK+BK=AC+BC的长;
即甲=乙=丙,
故选:D.
6.解:过点P作PH∥BC交AB于H,连接CH,PF,
∵APBE,
∴四边形APEB是平行四边形,
∴PE∥AB,PE=AB,
∵四边形BDEF是平行四边形,
∴EF∥BD,EF=BD,
即EF∥AB,
∴P,E,F共线,
设BD=a,
∵BD=AB,
∴PE=AB=4a,
则PF=PE﹣EF=3a,
∵PH∥BC,
∴S△HBC=S△PBC,
∵PF∥AB,
∴四边形BFPH是平行四边形,
∴BH=PF=3a,
∵S△HBC:S△ABC=BH:AB=3a:4a=3:4,
∴S△PBC:S△ABC=3:4.
故选:D.
7.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边AEOH,HOFD,EBNO,ONCF,AEFD,EBCF,ABNH,HNCD,ABCD都是平行四边形,共9个.
故选:B.
8.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边DEOH、DEFC、DHGA、BGOF、BGHC、BAEF、AGOE、CHOF和ABCD都是平行四边形,共9个.
故选:C.
9.解:A、∵∠BDC=∠BCD,
∴BD=BC,
根据已知AD∥BC不能推出四边形ABCD是等腰梯形,故本选项错误;
B、根据∠ABC=∠DAB和AD∥BC不能推出四边形ABCD是等腰梯形,故本选项错误;
C、∵∠ADB=∠DAC,AD∥BC,
∴∠ADB=∠DAC=∠DBC=∠ACB,
∴OA=OD,OB=OC,
∴AC=BD,
∵AD∥BC,
∴四边形ABCD是等腰梯形,故本选项正确;
D、根据∠AOB=∠BOC,只能推出AC⊥BD,
再根据AD∥BC不能推出四边形ABCD是等腰梯形,故本选项错误.
故选:C.
10.解:因为已知两角分别为50°,80°,
则另外一个角为50°,
则沿与另一边平行的直线把80°的角剪掉,
得到的是个梯形且是个等腰梯形,
因为同一底上的两底角相等.
故选:B.
二.填空题(共5小题,满分30分)
11.解:(如图)利用全等三角形的对应边相等,分别让三条边重合(作为平行四边形的对角线),就可以得到三个不同的平行四边形
12.解:若要拼成平行四边形,即是分别让它们的一组对应边重合,另外两组对应边分别平行.
故能拼出3个.
故答案为:3.
13.解:连接AC交BD于G,AE交DF于H.
∵AB平行且等于ED,AF平行且等于CD,
∴四边形AEDB是平行四边形,四边形AFDC是平行四边形,
∴AD∥BD,AC∥FD,AE=BD,AC=FD,
∵FD⊥BD,
∴四边形AHDG是矩形,
∴AH=DG,且AE⊥DF,BD⊥AC,
∴EH=BG.
∴六边形的面积=平行四边形AFDC的面积+三角形ABC的面积+三角形EFD的面积=FD BD=24×18=432.
14.解:平行四边形有:PABD,PACE,PMND,PMQE,APMD,APNE,PQGA,PMEB和PCGM.
平行四四边形PABD,平行四边形PMND对角线长是1和;
平行四边形PACE和PMQE的对角线长是:和;
平行四边形APNE和PMEB的对角线长是2和2;
平行四边形PQGA和PCGM的对角线长是3和.
故答案为:1或或或2或3.
15.解:使四边形AECF是平行四边形.就要使AE∥CF,AE=CF,就要使△AEB≌△CFD,而在平行四边形中已有AB=CD,∠ABE=∠CDF,再加一个BE=DF,或BF=DE就可用SAS证△AEB≌△CFD,BE=DF,或BF=DE.
故答案为:BE=DF或BF=DE或∠BAE=∠DCF.
三.解答题(共5小题,满分40分)
16.解:BE=DF,BE∥DF
因为ABCD是平行四边形,所以OA=OC,OB=OD,
因为E,F分别是OA,OC的中点,所以OE=OF,
所以BFDE是平行四边形,所以BE=DF,BE∥DF
17.证明:∵BE∥DF,
∴∠BEC=∠DFA,
在△ADF和△CBE中,
∴△ADF≌△CBE(AAS),
∴BE=DF,
又∵BE∥DF,
∴四边形DEBF是平行四边形.
18.证明:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形DEBF是平行四边形.
19.(1)证明:∵AF平分∠BAD,
∴∠DAF=∠BAF=∠BAD.
∵BG平分∠ABC,
∴∠ABG=∠CBG=∠ABC.
∵四边形ABCD平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴∠BAD+∠ABC=180°,
即2∠BAF+2∠ABG=180°,
∴∠BAF+∠ABG=90°.
∴∠AEB=180°﹣(∠BAF+∠ABG)=180°﹣90°=90°.
∴AF⊥BG;
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AFD=∠DAF,
∴DF=AD,
∵AB∥CD,
∴∠ABG=∠CGB,
∴∠CBG=∠CGB,
∴CG=BC,
∵AD=BC.
∴DF=CG;
(2)解:∵DF=AD=6,
∴CG=DF=6.
∴CG+DF=12,
∵四边形ABCD平行四边形,
∴CD=AB=10.
∴10+FG=12,
∴FG=2,
过点B作BH∥AF交DC的延长线于点H.
∴∠GBH=∠AEB=90°.
∵AF∥BH,AB∥FH,
∴四边形ABHF为平行四边形.
∴BH=AF=8,FH=AB=10.
∴GH=FG+FH=2+10=12,
∴在Rt△BHG中:BG==.
∴FG的长度为2,BG的长度为4.
20.解:(1)如图所示:是等腰梯形;
(2)点P一定在两底的垂直平分线上.设点P(1,y),
点P也在两腰的中垂线上:=,
解得:y=﹣1,
故P(1,﹣1);
(3)当点P不在两腰的中垂线上时,设点P(1,m),
DC=CP,
=4,
解得:m=,
故P(1,).
