5.2平行线 知识点分类训练 2021-2022学年华东师大版七年级数学上册(word版含解析)
文档属性
| 名称 | 5.2平行线 知识点分类训练 2021-2022学年华东师大版七年级数学上册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 238.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 16:24:15 | ||
图片预览



文档简介
2021-2022学年华师大版七年级数学上册《5.2平行线》知识点分类训练(附答案)
一.平行线
1.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
2.在同一平面内,直线a、b、c中,若a⊥b,b∥c,则a、c的位置关系是 .
3.下列语句中:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;③两条不相交的直线叫做平行线;④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等;⑤不在同一直线上的四个点可画6条直线;⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.其中错误的有( )
A.2个 B.3个 C.4个 D.5个
4.在下列4个判断中:
①在同一平面内,不相交也不重合的两条线段一定平行;②在同一平面内,不相交也不重合的两条直线一定平行;③在同一平面内,不平行也不重合的两条线段一定相交;④在同一平面内,不平行也不重合的两条直线一定相交.正确判断的个数是( )
A.4 B.3 C.2 D.1
二.平行公理及推论
5.下列说法中,正确的个数为( )
(1)过一点有无数条直线与已知直线平行
(2)如果a∥b,a∥c,那么b∥c
(3)如果两线段不相交,那么它们就平行
(4)如果两直线不相交,那么它们就平行
A.1个 B.2个 C.3个 D.4个
6.下列说法错误的个数是( )
①经过一点有且只有一条直线与已知直线平行;
②垂直于同一条直线的两条直线互相平行;
③直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
④同一平面内不相交的两条直线叫做平行线.
A.1个 B.2个 C.3个 D.4个
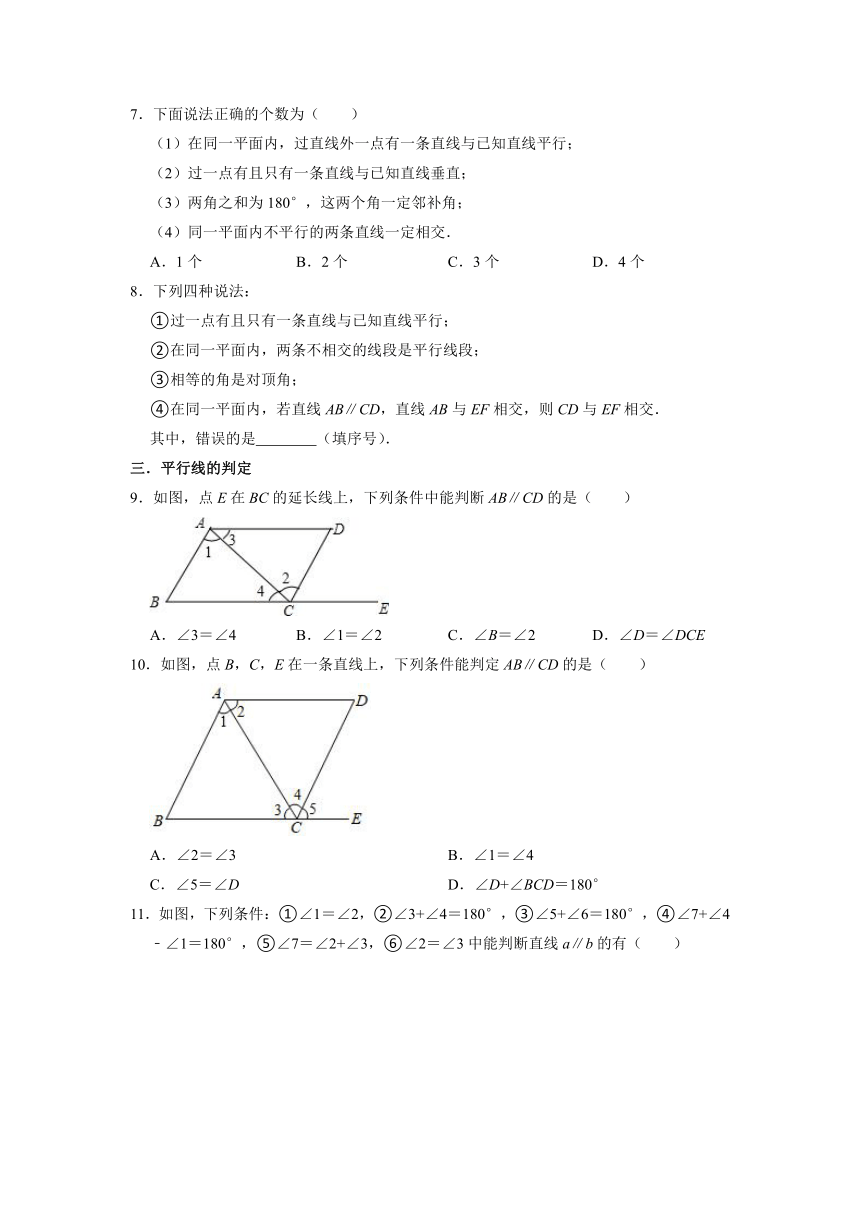
7.下面说法正确的个数为( )
(1)在同一平面内,过直线外一点有一条直线与已知直线平行;
(2)过一点有且只有一条直线与已知直线垂直;
(3)两角之和为180°,这两个角一定邻补角;
(4)同一平面内不平行的两条直线一定相交.
A.1个 B.2个 C.3个 D.4个
8.下列四种说法:
①过一点有且只有一条直线与已知直线平行;
②在同一平面内,两条不相交的线段是平行线段;
③相等的角是对顶角;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交.
其中,错误的是 (填序号).
三.平行线的判定
9.如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2 C.∠B=∠2 D.∠D=∠DCE
10.如图,点B,C,E在一条直线上,下列条件能判定AB∥CD的是( )
A.∠2=∠3 B.∠1=∠4
C.∠5=∠D D.∠D+∠BCD=180°
11.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
12.如图,将木条a,b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A.15° B.25° C.35° D.50°
13.如图,直线AB、CD被直线EF所截,GH是∠EGC的平分线,∠EGH=56°,∠EIB=68°,说明AB∥CD的理由.
解:因为GH是∠EGC的角平分线( ),
所以∠EGH=∠HGC=56°( ).
因为CD是条直线(已知),
所以∠HGC+∠EGH+∠IGD=180°( ).
所以∠IGD=68°.
因为∠EIB=68°(已知),
所以 = ( ).
所以AB∥CD( ).
14.将△ABC纸片沿DE折叠,其中∠B=∠C.
(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;
(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.
四.平行线的性质
15.在同一平面内,经过直线外一点,有且只有一条直线与已知直线( )
A.垂直 B.相交 C.平行 D.垂直或平行
16.如图,已知a∥b,直角三角板的直角顶点在直线b上,则下列结论错误的是( )
A.∠2=∠5 B.∠4﹣∠5=90° C.∠1+∠5=90° D.∠4+∠1=180°
17.如图,平面内,已知AB∥DE,∠ABC=130°,∠CDE=110°,则∠BCD的度数为( )
A.50° B.60 C.70° D.80°
18.如图,直线k∥l,∠3﹣∠2=∠2﹣∠1=d>0.其中∠3<90°,∠1=40°,则∠4的最大整数值是( )
A.108° B.110° C.114° D.115°
19.如图,AD∥BE,AC与BC相交于点C,且∠1=∠DAB,∠2=∠EBA.若∠C=45°,则n=( )
A.2 B.3 C.4 D.5
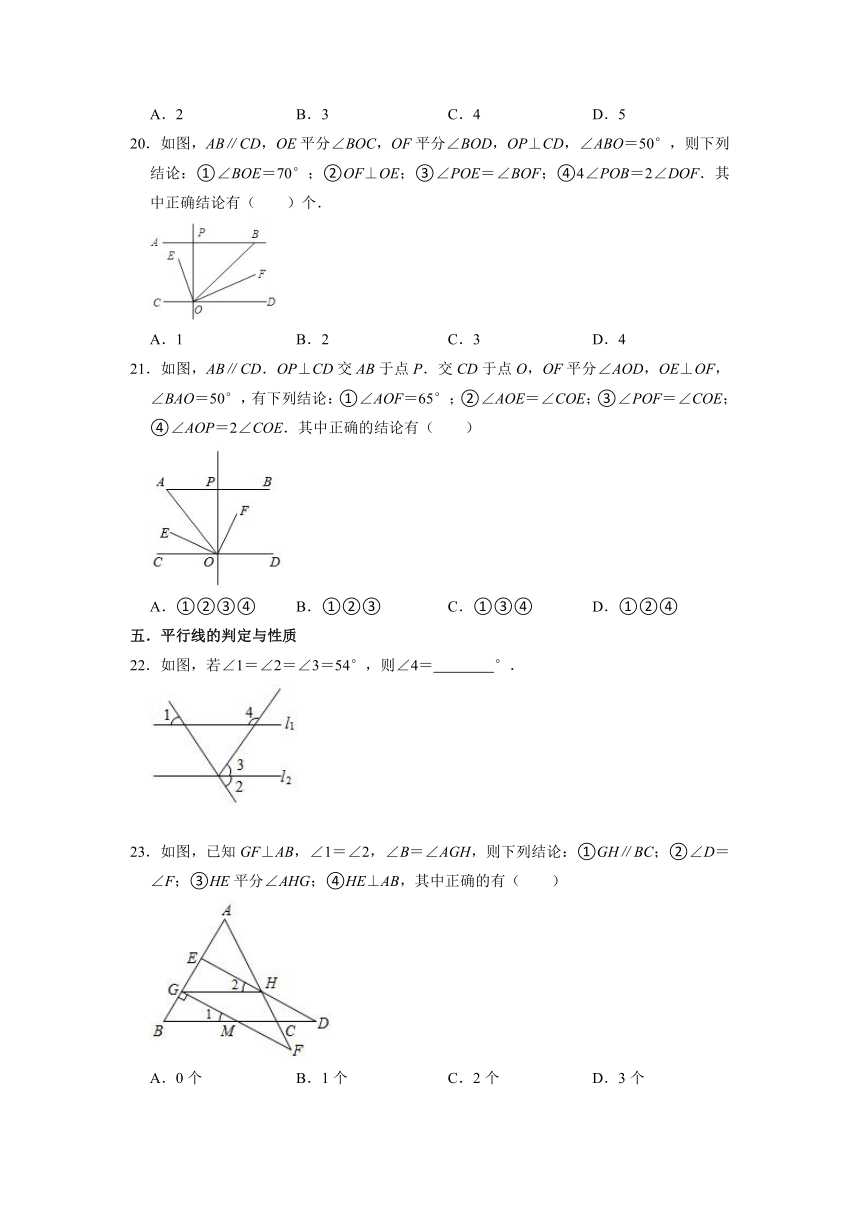
20.如图,AB∥CD,OE平分∠BOC,OF平分∠BOD,OP⊥CD,∠ABO=50°,则下列结论:①∠BOE=70°;②OF⊥OE;③∠POE=∠BOF;④4∠POB=2∠DOF.其中正确结论有( )个.
A.1 B.2 C.3 D.4
21.如图,AB∥CD.OP⊥CD交AB于点P.交CD于点O,OF平分∠AOD,OE⊥OF,∠BAO=50°,有下列结论:①∠AOF=65°;②∠AOE=∠COE;③∠POF=∠COE;④∠AOP=2∠COE.其中正确的结论有( )
A.①②③④ B.①②③ C.①③④ D.①②④
五.平行线的判定与性质
22.如图,若∠1=∠2=∠3=54°,则∠4= °.
23.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
24.将一副三角板按如图放置,则下列结论:①∠1=∠3;②∠CAD+∠2=180°;③若∠1=45°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
25.如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
六.平行线之间的距离
26.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和b之间的距离是( )
A.2cm B.6cm C.8cm D.2cm或8cm
27.平行线a、b之间的距离为8cm,若点P是直线a上一点,点Q是直线b上一点,则PQ 5cm.(填“<、>、≤、≥或=”)
28.如图:AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为 .
参考答案
一.平行线
1.解:①两点之间的所有连线中,线段最短,故①说法正确.
②相等的角不一定是对顶角,故②说法错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③说法错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④说法错误.
⑤两点之间的距离是两点间的线段的长度,故⑤说法错误.
⑥在同一平面内,两不重合的直线的位置关系只有两种:相交和平行,故⑥说法正确.
综上所述,正确的结论有2个.
故选:B.
2.解:∵c∥b,a⊥b,
∴c⊥a.
故答案为c⊥a
3.解:①一条直线有无数条垂线,故①错误;
②不相等的两个角一定不是对顶角,故②正确;
③在同一平面内,两条不相交的直线叫做平行线,故③错误;
④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等或互补,故④错误;
⑤不在同一直线上的四个点可画4或6条直线,故⑤错误;
⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角,故⑥正确.
所以错误的有4个.
故选:C.
4.解:在同一平面内,不相交也不重合的两条直线一定平行,故①错误,②正确;
在同一平面内,不平行也不重合的两条直线一定相交故,③错误,④正确.
故正确判断的个数是2.
故选:C.
二.平行公理及推论
5.解:(1)过直线外一点有且只有一条直线与已知直线平行,故错误;
(2)根据平行公理的推论,正确;
(3)线段的长度是有限的,不相交也不一定平行,故错误;
(4)应该是“在同一平面内”,故错误.
正确的只有一个,故选A.
6.解:①经过直线外一点有且只有一条直线与已知直线平行,故①错误;
②在同一平面内,垂直于同一条直线的两条直线互相平行,故②错误;
③直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离,故③错误;
④同一平面内不相交的两条直线叫做平行线,故④正确;
故选:C.
7.解:在同一平面内,过直线外一点有一条直线和已知直线平行,故(1)正确;
只有在同一平面内,过一点有且只有一条直线和已知直线垂直,故(2)错误;
如图:
∠ABC=∠DEF=90°,且∠ABC+∠DEF=180°,但是两角不是邻补角,故(3)错误;
同一平面内不平行的两条直线一定相交正确,
因为不特别指出时,一般认为,两条直线重合就是同一条直线,所以所提出的命题是正确的,故(4)正确.
即正确的个数是2个.
故选:B.
8.解:∵过直线外一点有且只有一条直线与已知直线平行,∴①错误;
∵在同一平面内,两条不相交的线段可能在一条直线上,说两线段是平行线段不对,∴②错误;
∵相等的角不一定是对顶角,∴③错误;
∵在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交,正确,∴④正确;
故答案为:①②③.
三.平行线的判定
9.解:∵∠1=∠2,
∴AB∥CD(内错角相等两直线平行),
故选:B.
10.解:A.因为∠2=∠3,
所以AD∥BC,故A选项不符合题意;
B.因为∠1=∠4,
所以AB∥DC,故B选项符合题意;
C.因为∠5=∠D,
所以AD∥BC,故C选项不符合题意;
D.因为∠D+∠BCD=180°,
所以AD∥BC,故A选项不符合题意;
故选:B.
11.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠7+∠4﹣∠1=180°,∠7=∠1+∠3,可得∠3+∠4=180°,即可得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠2=∠3,不能得到a∥b;
故能判断直线a∥b的有5个.
故选:C.
12.解:∵∠AOC=∠2=50°时,OA∥b,
∴要使木条a与b平行,木条a旋转的度数至少是85°﹣50°=35°.
故选:C.
13.解:因为GH是∠EGC的角平分线(已知),
所以∠EGH=∠HGC=56°(角平分线的定义),
因为CD是条直线(已知),
所以∠HGC+∠EGH+∠IGD=180°(平角的定义),
所以∠IGD=68°,
因为∠EIB=68°(已知),
所以∠IGD=∠EIB(等量代换),
所以AB∥CD(同位角相等,两直线平行).
故答案为:已知,角平分线的定义,平角的定义,∠IGD,∠EIB,等量代换,同位角相等,两直线平行.
14.解:(1)AB与DF平行.理由如下:
由翻折,得∠DFC=∠C.
又∵∠B=∠C,
∴∠B=∠DFC,
∴AB∥DF.
(2)连接GC,如图所示.
由翻折,得∠DGE=∠ACB.
∵∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.
∵∠B=∠ACB,
∴∠1+∠2=2∠B.
四.平行线的性质
15.解:根据平行线的推论以及垂线的推论,在同一面平面内,经过直线外一点,有且只有一条直线与已知直线平行或垂直.
故选:D.
16.解:A.∵a∥b,
∴∠2=∠3,
而∠3不一定等于∠5,
∴∠2也不一定等于∠5,
故A选项符合题意;
B.∵∠3+∠4=180°,∠3+∠5=90°,
∴∠4﹣∠5=180°﹣90°=90°,
故B选项不符合题意;
C.∵a∥b,
∴∠1=∠3,
∵∠3+∠5=90°,
∴∠1+∠5=90°,
故C选项不符合题意;
D..∵a∥b,
∴∠1=∠3,
∵∠3+∠4=180°,
∴∠4+∠1=180°,
故D选项不符合题意.
故选:A.
17.解:如图,延长ED至N,并交BC于点M.
∵AB∥DE,
∴∠ABC=∠NMC=130°.
∴∠CMD=180°﹣∠NMC=180°﹣130°=50°.
又∵∠CDE=∠C+∠CMD,
∴∠C=∠CDE﹣∠CMD=110°﹣50°=60°.
故选:B.
18.解:延长CD交直线b于F,延长DC交直线a于B,如图所示:
∵k∥l,
∴∠ABC=∠DFE,
∵∠ABC=∠2﹣∠1,∠DFE=∠4﹣∠3,
∴∠4﹣∠3=∠3﹣∠2,
∴∠4=2∠3﹣∠2,
又∵∠3﹣∠2=∠2﹣∠1,∠1=40°,
∴2∠2=∠3+40°,
∴2∠4=4∠3﹣2∠2=4∠3﹣∠3﹣40°=3∠3﹣40°,
∴∠3=,
而∠3<90°,
∴<90°,
∴∠4<115°,
∴∠4的最大可能的整数值是114°.
故选:C.
19.解:如图,过C点作CF∥BE,
∵AD∥BE,
∴CF∥AD∥BE,
∴∠1=∠ACF,∠2=∠BCF,∠DAB+∠EBA=180°,
∴∠1+∠2=∠ACF+∠BCF=∠C=45°,
∵∠1=∠DAB,∠2=∠EBA,
∴∠1+∠2=∠DAB+∠EBA=(∠DAB+∠EBA)=45°,
∴n=4.
故选:C.
20.解:∵AB∥CD,
∴∠ABO=∠BOD=50°,
∴∠BOC=180°﹣50°=130°,
∵OE平分∠BOC,
∴∠BOE=×130°=65°;所以①错误;
∵OE平分∠BOC,OF平分∠BOD,
∴∠BOE=,∠BOF=,
∵∠BOC+∠BOD=180°,
∴∠EOF=∠BOE+∠BOF=(∠BOC+∠BOD)=90°,
∴OE⊥OF,所以②正确;
∵OP⊥CD,
∴∠COP=90°,
∴∠EOF=∠POD=90°,
∴∠POE=90°﹣∠POF,∠DOF=90°﹣∠POF,
∴∠POE=∠DOF,
∵∠BOF=∠DOF,
∴∠POE=∠BOF;所以③正确;
∵AB∥CD,OP⊥CD,
∴OP⊥AB,∠BOD=∠ABO=50°,
∴∠BPO=90°,
∴∠POB=90°﹣∠PBO=40°,
∵OF平分∠BOD,
∴∠DOF=∠BOD=25°,
∴4∠POB=160°,2∠DOF=50°,
∴4∠POB≠2∠DOF所以④错误.
故选:B.
21.解:∵AB∥CD,∠BAO=50°,
∴∠AOD=180°﹣∠BAO=130°,∠COA=∠BAO=50°,
∵OF平分∠AOD,
∴∠AOF=∠DOF=∠AOD=65°,故①正确;
∵OE⊥OF,
∴∠AOE=90°﹣∠AOF=25°,
∴∠COE=∠COA﹣∠AOE=25°,
∴∠AOE=∠COE,故②正确;
∵OP⊥CD交AB于点P,
∴∠POF=90°﹣∠DOF=25°,
∴∠POF=∠COE,故③正确;
∵∠AOP=∠EOF﹣∠POF﹣∠AOE
=90°﹣25°﹣25°
=40°,
2∠COE=50°,
∴∠AOP≠2∠COE,故④错误.
综上所述,正确的有①②③.
故选:B.
五.平行线的判定与性质
22.解:∵∠1=∠6,∠1=∠2,
∴∠6=∠2,
∴l1∥l2,
∴∠3=∠5,
∴∠4+∠5=∠4+∠3=180°,
∴∠4=180°﹣∠5=180°﹣∠3=180°﹣54°=126°.
故答案为:126°.
23.解:∵∠B=∠AGH,
∴GH∥BC,故①正确;
∴∠1=∠HGF,
∵∠1=∠2,
∴∠2=∠HGF,
∴DE∥GF,
∴∠D=∠DMF,
根据已知条件不能推出∠F也等于∠DMF,故②错误;
∵DE∥GF,
∴∠F=∠AHE,
∵∠D=∠1=∠2,
∴∠2不一定等于∠AHE,故③错误;
∵GF⊥AB,GF∥HE,
∴HE⊥AB,故④正确;
即正确的个数是2,
故选:C.
24.解:∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
故①正确;
∵∠CAD+∠2=∠1+∠2+∠3+∠2=90°+90°=180°,
故②正确;
∵∠1=45°,
∴∠3=∠B=45°,
∴BC∥AD.
故③正确;
∵∠2=30°,
∴∠1=∠E=60°,
∴AC∥DE,
∴∠4=∠C,
故④正确.
故选:D.
25.解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°﹣90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°﹣90°=45°,
∴∠F=180°﹣(∠FAD+∠FDA)=180﹣45°=135°,故④正确.
综上所述正确的有:①③④,共3个.
故选:C.
六.平行线之间的距离
26.解:如图1,直线a和b之间的距离为:5﹣3=2(cm);
如图2,直线a和b之间的距离为:5+3=8(cm).
故选:D.
27.解:∵a∥b,ab之间的距离是8cm,
当PQ⊥直线b时,PQ=8cm,
当PQ和直线b不垂直时,PQ>8cm,
即PQ≥8cm,
∴PQ>5cm,
故答案为:>.
28.解:作DG⊥BC于G,AH⊥BC于H,
∵AD∥BC,∴AH=DG,
又AB∥CD,
∴四边形ABCD是平行四边形,
∴BC=AD=5,又BE=8,
∴CE=3,又△DCE的面积为6,
∴DG=4,
∴四边形ABCD的面积=BC×AH=20,
故答案为:20.
一.平行线
1.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
2.在同一平面内,直线a、b、c中,若a⊥b,b∥c,则a、c的位置关系是 .
3.下列语句中:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;③两条不相交的直线叫做平行线;④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等;⑤不在同一直线上的四个点可画6条直线;⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.其中错误的有( )
A.2个 B.3个 C.4个 D.5个
4.在下列4个判断中:
①在同一平面内,不相交也不重合的两条线段一定平行;②在同一平面内,不相交也不重合的两条直线一定平行;③在同一平面内,不平行也不重合的两条线段一定相交;④在同一平面内,不平行也不重合的两条直线一定相交.正确判断的个数是( )
A.4 B.3 C.2 D.1
二.平行公理及推论
5.下列说法中,正确的个数为( )
(1)过一点有无数条直线与已知直线平行
(2)如果a∥b,a∥c,那么b∥c
(3)如果两线段不相交,那么它们就平行
(4)如果两直线不相交,那么它们就平行
A.1个 B.2个 C.3个 D.4个
6.下列说法错误的个数是( )
①经过一点有且只有一条直线与已知直线平行;
②垂直于同一条直线的两条直线互相平行;
③直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
④同一平面内不相交的两条直线叫做平行线.
A.1个 B.2个 C.3个 D.4个
7.下面说法正确的个数为( )
(1)在同一平面内,过直线外一点有一条直线与已知直线平行;
(2)过一点有且只有一条直线与已知直线垂直;
(3)两角之和为180°,这两个角一定邻补角;
(4)同一平面内不平行的两条直线一定相交.
A.1个 B.2个 C.3个 D.4个
8.下列四种说法:
①过一点有且只有一条直线与已知直线平行;
②在同一平面内,两条不相交的线段是平行线段;
③相等的角是对顶角;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交.
其中,错误的是 (填序号).
三.平行线的判定
9.如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2 C.∠B=∠2 D.∠D=∠DCE
10.如图,点B,C,E在一条直线上,下列条件能判定AB∥CD的是( )
A.∠2=∠3 B.∠1=∠4
C.∠5=∠D D.∠D+∠BCD=180°
11.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠7+∠4﹣∠1=180°,⑤∠7=∠2+∠3,⑥∠2=∠3中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
12.如图,将木条a,b与c钉在一起,∠1=85°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A.15° B.25° C.35° D.50°
13.如图,直线AB、CD被直线EF所截,GH是∠EGC的平分线,∠EGH=56°,∠EIB=68°,说明AB∥CD的理由.
解:因为GH是∠EGC的角平分线( ),
所以∠EGH=∠HGC=56°( ).
因为CD是条直线(已知),
所以∠HGC+∠EGH+∠IGD=180°( ).
所以∠IGD=68°.
因为∠EIB=68°(已知),
所以 = ( ).
所以AB∥CD( ).
14.将△ABC纸片沿DE折叠,其中∠B=∠C.
(1)如图1,点C落在BC边上的点F处,AB与DF是否平行?请说明理由;
(2)如图2,点C落在四边形ABCD内部的点G处,探索∠B与∠1+∠2之间的数量关系,并说明理由.
四.平行线的性质
15.在同一平面内,经过直线外一点,有且只有一条直线与已知直线( )
A.垂直 B.相交 C.平行 D.垂直或平行
16.如图,已知a∥b,直角三角板的直角顶点在直线b上,则下列结论错误的是( )
A.∠2=∠5 B.∠4﹣∠5=90° C.∠1+∠5=90° D.∠4+∠1=180°
17.如图,平面内,已知AB∥DE,∠ABC=130°,∠CDE=110°,则∠BCD的度数为( )
A.50° B.60 C.70° D.80°
18.如图,直线k∥l,∠3﹣∠2=∠2﹣∠1=d>0.其中∠3<90°,∠1=40°,则∠4的最大整数值是( )
A.108° B.110° C.114° D.115°
19.如图,AD∥BE,AC与BC相交于点C,且∠1=∠DAB,∠2=∠EBA.若∠C=45°,则n=( )
A.2 B.3 C.4 D.5
20.如图,AB∥CD,OE平分∠BOC,OF平分∠BOD,OP⊥CD,∠ABO=50°,则下列结论:①∠BOE=70°;②OF⊥OE;③∠POE=∠BOF;④4∠POB=2∠DOF.其中正确结论有( )个.
A.1 B.2 C.3 D.4
21.如图,AB∥CD.OP⊥CD交AB于点P.交CD于点O,OF平分∠AOD,OE⊥OF,∠BAO=50°,有下列结论:①∠AOF=65°;②∠AOE=∠COE;③∠POF=∠COE;④∠AOP=2∠COE.其中正确的结论有( )
A.①②③④ B.①②③ C.①③④ D.①②④
五.平行线的判定与性质
22.如图,若∠1=∠2=∠3=54°,则∠4= °.
23.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
24.将一副三角板按如图放置,则下列结论:①∠1=∠3;②∠CAD+∠2=180°;③若∠1=45°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C,其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
25.如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
六.平行线之间的距离
26.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和b之间的距离是( )
A.2cm B.6cm C.8cm D.2cm或8cm
27.平行线a、b之间的距离为8cm,若点P是直线a上一点,点Q是直线b上一点,则PQ 5cm.(填“<、>、≤、≥或=”)
28.如图:AB∥CD,AD∥BC,AD=5,BE=8,△DCE的面积为6,则四边形ABCD的面积为 .
参考答案
一.平行线
1.解:①两点之间的所有连线中,线段最短,故①说法正确.
②相等的角不一定是对顶角,故②说法错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③说法错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④说法错误.
⑤两点之间的距离是两点间的线段的长度,故⑤说法错误.
⑥在同一平面内,两不重合的直线的位置关系只有两种:相交和平行,故⑥说法正确.
综上所述,正确的结论有2个.
故选:B.
2.解:∵c∥b,a⊥b,
∴c⊥a.
故答案为c⊥a
3.解:①一条直线有无数条垂线,故①错误;
②不相等的两个角一定不是对顶角,故②正确;
③在同一平面内,两条不相交的直线叫做平行线,故③错误;
④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等或互补,故④错误;
⑤不在同一直线上的四个点可画4或6条直线,故⑤错误;
⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角,故⑥正确.
所以错误的有4个.
故选:C.
4.解:在同一平面内,不相交也不重合的两条直线一定平行,故①错误,②正确;
在同一平面内,不平行也不重合的两条直线一定相交故,③错误,④正确.
故正确判断的个数是2.
故选:C.
二.平行公理及推论
5.解:(1)过直线外一点有且只有一条直线与已知直线平行,故错误;
(2)根据平行公理的推论,正确;
(3)线段的长度是有限的,不相交也不一定平行,故错误;
(4)应该是“在同一平面内”,故错误.
正确的只有一个,故选A.
6.解:①经过直线外一点有且只有一条直线与已知直线平行,故①错误;
②在同一平面内,垂直于同一条直线的两条直线互相平行,故②错误;
③直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离,故③错误;
④同一平面内不相交的两条直线叫做平行线,故④正确;
故选:C.
7.解:在同一平面内,过直线外一点有一条直线和已知直线平行,故(1)正确;
只有在同一平面内,过一点有且只有一条直线和已知直线垂直,故(2)错误;
如图:
∠ABC=∠DEF=90°,且∠ABC+∠DEF=180°,但是两角不是邻补角,故(3)错误;
同一平面内不平行的两条直线一定相交正确,
因为不特别指出时,一般认为,两条直线重合就是同一条直线,所以所提出的命题是正确的,故(4)正确.
即正确的个数是2个.
故选:B.
8.解:∵过直线外一点有且只有一条直线与已知直线平行,∴①错误;
∵在同一平面内,两条不相交的线段可能在一条直线上,说两线段是平行线段不对,∴②错误;
∵相等的角不一定是对顶角,∴③错误;
∵在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交,正确,∴④正确;
故答案为:①②③.
三.平行线的判定
9.解:∵∠1=∠2,
∴AB∥CD(内错角相等两直线平行),
故选:B.
10.解:A.因为∠2=∠3,
所以AD∥BC,故A选项不符合题意;
B.因为∠1=∠4,
所以AB∥DC,故B选项符合题意;
C.因为∠5=∠D,
所以AD∥BC,故C选项不符合题意;
D.因为∠D+∠BCD=180°,
所以AD∥BC,故A选项不符合题意;
故选:B.
11.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠7+∠4﹣∠1=180°,∠7=∠1+∠3,可得∠3+∠4=180°,即可得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠2=∠3,不能得到a∥b;
故能判断直线a∥b的有5个.
故选:C.
12.解:∵∠AOC=∠2=50°时,OA∥b,
∴要使木条a与b平行,木条a旋转的度数至少是85°﹣50°=35°.
故选:C.
13.解:因为GH是∠EGC的角平分线(已知),
所以∠EGH=∠HGC=56°(角平分线的定义),
因为CD是条直线(已知),
所以∠HGC+∠EGH+∠IGD=180°(平角的定义),
所以∠IGD=68°,
因为∠EIB=68°(已知),
所以∠IGD=∠EIB(等量代换),
所以AB∥CD(同位角相等,两直线平行).
故答案为:已知,角平分线的定义,平角的定义,∠IGD,∠EIB,等量代换,同位角相等,两直线平行.
14.解:(1)AB与DF平行.理由如下:
由翻折,得∠DFC=∠C.
又∵∠B=∠C,
∴∠B=∠DFC,
∴AB∥DF.
(2)连接GC,如图所示.
由翻折,得∠DGE=∠ACB.
∵∠1=∠DGC+∠DCG,∠2=∠EGC+∠ECG,
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.
∵∠B=∠ACB,
∴∠1+∠2=2∠B.
四.平行线的性质
15.解:根据平行线的推论以及垂线的推论,在同一面平面内,经过直线外一点,有且只有一条直线与已知直线平行或垂直.
故选:D.
16.解:A.∵a∥b,
∴∠2=∠3,
而∠3不一定等于∠5,
∴∠2也不一定等于∠5,
故A选项符合题意;
B.∵∠3+∠4=180°,∠3+∠5=90°,
∴∠4﹣∠5=180°﹣90°=90°,
故B选项不符合题意;
C.∵a∥b,
∴∠1=∠3,
∵∠3+∠5=90°,
∴∠1+∠5=90°,
故C选项不符合题意;
D..∵a∥b,
∴∠1=∠3,
∵∠3+∠4=180°,
∴∠4+∠1=180°,
故D选项不符合题意.
故选:A.
17.解:如图,延长ED至N,并交BC于点M.
∵AB∥DE,
∴∠ABC=∠NMC=130°.
∴∠CMD=180°﹣∠NMC=180°﹣130°=50°.
又∵∠CDE=∠C+∠CMD,
∴∠C=∠CDE﹣∠CMD=110°﹣50°=60°.
故选:B.
18.解:延长CD交直线b于F,延长DC交直线a于B,如图所示:
∵k∥l,
∴∠ABC=∠DFE,
∵∠ABC=∠2﹣∠1,∠DFE=∠4﹣∠3,
∴∠4﹣∠3=∠3﹣∠2,
∴∠4=2∠3﹣∠2,
又∵∠3﹣∠2=∠2﹣∠1,∠1=40°,
∴2∠2=∠3+40°,
∴2∠4=4∠3﹣2∠2=4∠3﹣∠3﹣40°=3∠3﹣40°,
∴∠3=,
而∠3<90°,
∴<90°,
∴∠4<115°,
∴∠4的最大可能的整数值是114°.
故选:C.
19.解:如图,过C点作CF∥BE,
∵AD∥BE,
∴CF∥AD∥BE,
∴∠1=∠ACF,∠2=∠BCF,∠DAB+∠EBA=180°,
∴∠1+∠2=∠ACF+∠BCF=∠C=45°,
∵∠1=∠DAB,∠2=∠EBA,
∴∠1+∠2=∠DAB+∠EBA=(∠DAB+∠EBA)=45°,
∴n=4.
故选:C.
20.解:∵AB∥CD,
∴∠ABO=∠BOD=50°,
∴∠BOC=180°﹣50°=130°,
∵OE平分∠BOC,
∴∠BOE=×130°=65°;所以①错误;
∵OE平分∠BOC,OF平分∠BOD,
∴∠BOE=,∠BOF=,
∵∠BOC+∠BOD=180°,
∴∠EOF=∠BOE+∠BOF=(∠BOC+∠BOD)=90°,
∴OE⊥OF,所以②正确;
∵OP⊥CD,
∴∠COP=90°,
∴∠EOF=∠POD=90°,
∴∠POE=90°﹣∠POF,∠DOF=90°﹣∠POF,
∴∠POE=∠DOF,
∵∠BOF=∠DOF,
∴∠POE=∠BOF;所以③正确;
∵AB∥CD,OP⊥CD,
∴OP⊥AB,∠BOD=∠ABO=50°,
∴∠BPO=90°,
∴∠POB=90°﹣∠PBO=40°,
∵OF平分∠BOD,
∴∠DOF=∠BOD=25°,
∴4∠POB=160°,2∠DOF=50°,
∴4∠POB≠2∠DOF所以④错误.
故选:B.
21.解:∵AB∥CD,∠BAO=50°,
∴∠AOD=180°﹣∠BAO=130°,∠COA=∠BAO=50°,
∵OF平分∠AOD,
∴∠AOF=∠DOF=∠AOD=65°,故①正确;
∵OE⊥OF,
∴∠AOE=90°﹣∠AOF=25°,
∴∠COE=∠COA﹣∠AOE=25°,
∴∠AOE=∠COE,故②正确;
∵OP⊥CD交AB于点P,
∴∠POF=90°﹣∠DOF=25°,
∴∠POF=∠COE,故③正确;
∵∠AOP=∠EOF﹣∠POF﹣∠AOE
=90°﹣25°﹣25°
=40°,
2∠COE=50°,
∴∠AOP≠2∠COE,故④错误.
综上所述,正确的有①②③.
故选:B.
五.平行线的判定与性质
22.解:∵∠1=∠6,∠1=∠2,
∴∠6=∠2,
∴l1∥l2,
∴∠3=∠5,
∴∠4+∠5=∠4+∠3=180°,
∴∠4=180°﹣∠5=180°﹣∠3=180°﹣54°=126°.
故答案为:126°.
23.解:∵∠B=∠AGH,
∴GH∥BC,故①正确;
∴∠1=∠HGF,
∵∠1=∠2,
∴∠2=∠HGF,
∴DE∥GF,
∴∠D=∠DMF,
根据已知条件不能推出∠F也等于∠DMF,故②错误;
∵DE∥GF,
∴∠F=∠AHE,
∵∠D=∠1=∠2,
∴∠2不一定等于∠AHE,故③错误;
∵GF⊥AB,GF∥HE,
∴HE⊥AB,故④正确;
即正确的个数是2,
故选:C.
24.解:∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,
故①正确;
∵∠CAD+∠2=∠1+∠2+∠3+∠2=90°+90°=180°,
故②正确;
∵∠1=45°,
∴∠3=∠B=45°,
∴BC∥AD.
故③正确;
∵∠2=30°,
∴∠1=∠E=60°,
∴AC∥DE,
∴∠4=∠C,
故④正确.
故选:D.
25.解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°﹣90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°﹣90°=45°,
∴∠F=180°﹣(∠FAD+∠FDA)=180﹣45°=135°,故④正确.
综上所述正确的有:①③④,共3个.
故选:C.
六.平行线之间的距离
26.解:如图1,直线a和b之间的距离为:5﹣3=2(cm);
如图2,直线a和b之间的距离为:5+3=8(cm).
故选:D.
27.解:∵a∥b,ab之间的距离是8cm,
当PQ⊥直线b时,PQ=8cm,
当PQ和直线b不垂直时,PQ>8cm,
即PQ≥8cm,
∴PQ>5cm,
故答案为:>.
28.解:作DG⊥BC于G,AH⊥BC于H,
∵AD∥BC,∴AH=DG,
又AB∥CD,
∴四边形ABCD是平行四边形,
∴BC=AD=5,又BE=8,
∴CE=3,又△DCE的面积为6,
∴DG=4,
∴四边形ABCD的面积=BC×AH=20,
故答案为:20.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
