14.2勾股定理的应用 同步达标训练 2021-2022学年华东师大版八年级数学上册(word版含解析)
文档属性
| 名称 | 14.2勾股定理的应用 同步达标训练 2021-2022学年华东师大版八年级数学上册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 268.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 00:00:00 | ||
图片预览




文档简介
2021-2022学年华师大版八年级数学上册《14.2勾股定理的应用》同步达标训练(附答案)
1.如图,若圆柱的底面周长是50cm,高是120cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.170cm B.70cm C.145cm D.130cm
2.如图,学校B前面有一条笔直的公路,学生放学后走AB、BC两条路可到达公路,经测量BC=6km,BA=8km,AC=10km,现需修建一条公路从学校B到公路,则学校B到公路的最短距离为( )
A.4.8km B.9.6km C.2.4km D.5km
3.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20km B.14km C.11km D.10km
4.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.则这只蚂蚁沿着台阶面爬行的最短路程是( )
A.18 B.15 C.12 D.8
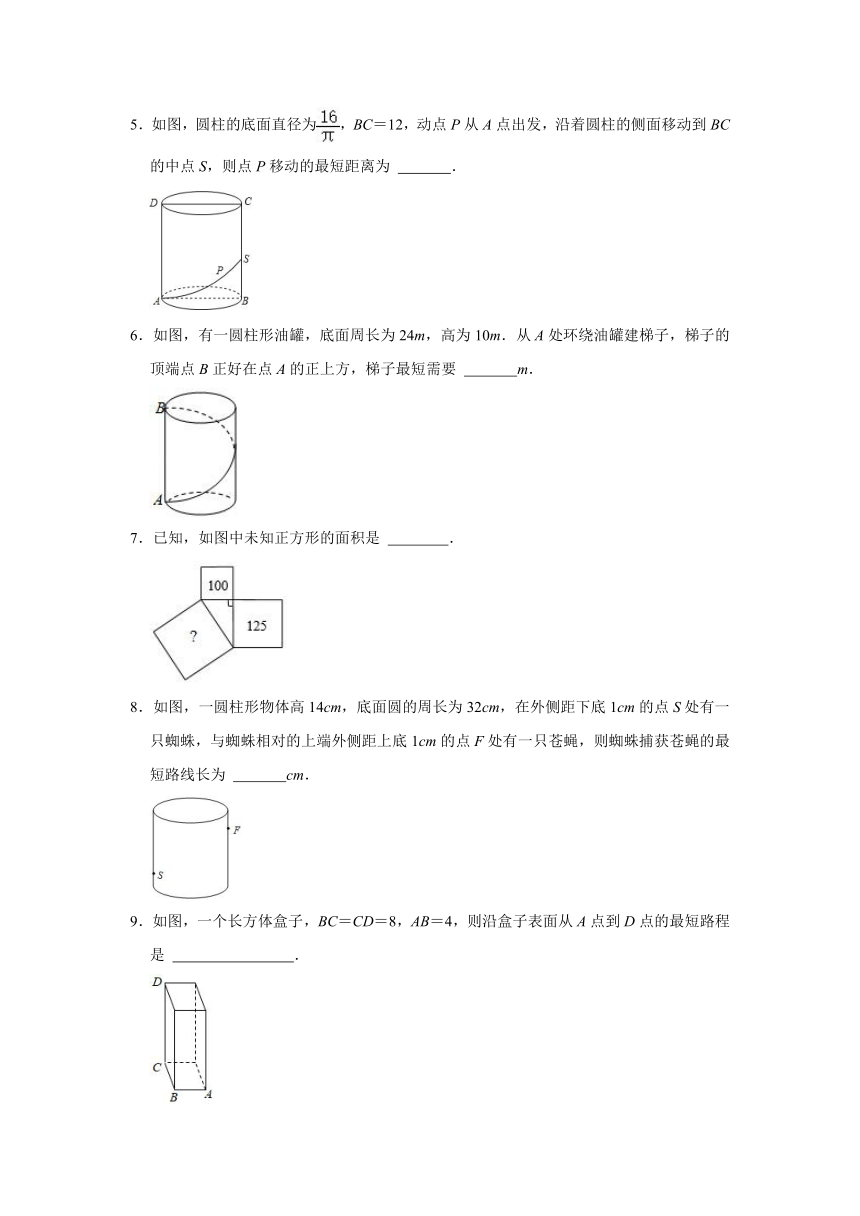
5.如图,圆柱的底面直径为,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S,则点P移动的最短距离为 .
6.如图,有一圆柱形油罐,底面周长为24m,高为10m.从A处环绕油罐建梯子,梯子的顶端点B正好在点A的正上方,梯子最短需要 m.
7.已知,如图中未知正方形的面积是 .
8.如图,一圆柱形物体高14cm,底面圆的周长为32cm,在外侧距下底1cm的点S处有一只蜘蛛,与蜘蛛相对的上端外侧距上底1cm的点F处有一只苍蝇,则蜘蛛捕获苍蝇的最短路线长为 cm.
9.如图,一个长方体盒子,BC=CD=8,AB=4,则沿盒子表面从A点到D点的最短路程是 .
10.为响应政府的“公园城市建设”号召,某小区进行小范围绿化,要在一块四边形空地上种植草皮,经测∠B=90°,AB=6米,BC=8米,CD=24米,AD=26米,如果种植草皮费用是300元/米2,那么共需投入多少钱?
11.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有学校,点A到公路MN的距离为120m,现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时130m范围以内都会受到噪音的影响,请你算出该学校受影响的时间多长?
12.如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报.某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.如果这艘轮船不改变航向和速度,那么从接到警报开始,经过多长时间它会进入台风影响区?(结果精确到0.01h,)
13.“新冠肺炎”疫情牵动着14亿中华儿女的心,渠县人民政府积极响应国家号召,及时对广大人民群众进行疫情防控宣传.如图,一笔直公路MN,村庄A到公路MN的距离为600m,若在宣传车P方圆1000m以内能听到广播宣传,那么宣传车P在公路MN上沿MN方向行驶时:
(1)村庄能否听到宣传?请说明理由.
(2)如果能听到,已知宣传车的速度是200m/min,那么村庄总共能听到多长时间的宣传?
14.如图所示,AB=DE=25,AC=24,∠C=90°.
(1)这个梯子底端B离墙有多少米?
(2)如果梯子的顶端下滑的距离AD=4m,求梯子的底部B在水平方向滑动的距离BE的长.
15.如图,一架长为5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC为3米.
(1)求BC的长;
(2)如果梯子的顶端B沿墙向下滑动2米,问梯子的底端向外移动了多少米?
16.位于沈阳周边的红河峡谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A拉回点B的位置(如图).在离水面高度为8m的岸上点C,工作人员用绳子拉船移动,开始时绳子AC的长为17m,工作人员以0.7米/秒的速度拉绳子,经过10秒后游船移动到点D的位置,问此时游船移动的距离AD的长是多少?
17.三水九道谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A拉回点B的位置(如图).在离水面高度为8m的岸上点C,工作人员用绳子拉船移动,开始时绳子AC的长为17m,经过10秒后游船移动到点D的位置,此时BD=6m,问工作人员拉绳子的速度是多少?
18.在甲村至乙村的公路旁有一块山地需要开发,现有一C处需要爆破,已知点C与公路上的停靠点A的距离为800米,与公路上另一停靠点B的距离为600米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径450米范围内不得进入,问在进行爆破时,公路AB段是否有危险需要暂时封锁?请通过计算进行说明.
19.如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=20米,CA⊥AB且CA=12米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=12米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体移动距离BD的长度.
20.某快递公司为了给客户提供“安全、快速”的优质服务,购置了一台无人机往返A,B,C三地运输货物,如图所示,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区A位于快递站点B的南偏东55°方向,无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到A需飞行15分钟.请求出无人机从幸福小区C飞到沁苑小区A所需要的时间.
参考答案
1.解:如图,圆柱侧面展开图是矩形,
矩形的长为120cm,宽为圆柱的底面周长50cm,
根据勾股定理得:
AB==130(cm),
根据两点之间线段最短,可得丝线的最小长度为130cm,
故选:D.
2.解:过B作BD⊥AC,垂足为D,
∵62+82=102,
∴BC2+AB2=AC2,
∴∠ABC=90°,
∵S△ACB=AB CB=AC BD,
∴×6×8=×10×DB,
解得:BD=4.8,
∴学校B到公路的最短距离为4.8km,
故选:A.
3.解:过点B作BC⊥AC,垂足为C.
观察图形可知AC=AF﹣MF+MC=8﹣3+1=6(km),BC=2+5=7(km),
在Rt△ACB中,AB===10(km).
答:登陆点到宝藏埋藏点的直线距离是10km,
故选:D.
4.解:将台阶展开,如图,
因为AC=3×3+1×3=12,BC=9,
所以AB2=AC2+BC2=225,
所以AB=15,
所以蚂蚁爬行的最短线路为15.
故选:B.
5.解:如图所示,
∵圆柱的底面直径为,BC=12,
∴AB=××π=8,BS=BC=6,
∴AS==10.
故答案为:10.
6.解:将圆柱体的侧面展开,如图所示:
则AC=底面周长=24m,BC=10m,
在Rt△ABC中,AB==26(m),
故答案为:26.
7.解:∵100+125=225=152,
∴“?”所代表的正方形的面积=152=225.
故答案是:225.
8.解:如图展开后连接SF,求出SF的长就是捕获苍蝇充饥的蜘蛛所走的最短路径,
过S作SE⊥CD于E,
则SE=BC=×32=16(cm),
EF=14﹣1﹣1=12(cm),
在Rt△FES中,由勾股定理得:SF===20(cm),
答:捕获苍蝇充饥的蜘蛛所走的最短路径的长度是20cm,
故答案为:20.
9.解:如图,把正面和左面展开,形成一个平面,AD两点之间线段最短.
即AD===4;
如图,把正上面和上面展开,形成一个平面,AD两点之间线段最短.
即AD===4;
如图,把右面和上面展开,形成一个平面,AD两点之间线段最短.
AD==4;
故从A点到D点的最短路程为:4.
故答案为:4.
10.解:连接AC,
∵∠B=90°,
∴在Rt△ABC中,由勾股定理得AC===10(米),
在△ACD中,∵AC2+CD2=102+242=262=AD2,
∴△ACD是直角三角形,且∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD
=AB BC+AC CD
=×6×8+×10×24
=24+120
=144(平方米),
所以需费用300×144=43200(元).
∴需要投入43200元.
11.解:设卡车开到C处刚好开始受到影响,行驶到D处时结束了噪声的影响.
则有CA=DA=130m,
在Rt△ABC中,CB==50(m),
∴CD=2CB=100(m),
则该校受影响的时间为:100÷5=20(s).
答:该学校受影响的时间为20s,
12.解:设x小时后,就进入台风影响区,根据题意得出:
CE=30x千米,BB′=20x千米,
∵BC=500km,AB=300km,
∴AC=400km,
∴AE=400﹣30x,AB′=300﹣20x,
根据勾股定理得:AE2+AB′2=EB′2,
即(400﹣30x)2+(300﹣20x)2=2002,
解得:x1=≈8.35,x2=≈19.3(舍去),
答:轮船经8.35小时就进入台风影响区.
13.解:(1)村庄能听到宣传,理由如下:过点A作AB⊥MN于B,
∵村庄A到公路MN的距离为600米<1000米
∴村庄能听到宣传;
(2)如图:假设当宣讲车行驶到P点开始影响村庄,行驶Q点结束对村庄的影响,
则AP=AQ=1000米,AB=600米,
∴BP=PQ===800(米),
∴PQ=BP+BQ=800+800=1600(米),
∴影响村庄的时间为:1600÷200=8(分钟),
∴村庄总共能听到8分钟的宣传.
14.解:(1)由题意知AB=DE=25米,AC=24米,AD=4米,
在直角△ABC中,∠C=90°,
∴BC2+AC2=AB2,
∴米,
∴这个梯子底端离墙有7米;
(2)已知AD=4米,则CD=24﹣4=20(米),
在直角△CDE中,∠C=90°,
∴BD2+CE2=DE2,
∴(米),
∴BE=15﹣7=8(米),
答:梯子的底部在水平方向滑动了8m.
15.解:(1)∵一架长5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=3米,
∴BC==4(m),
答:BC的长为4m;
(2)∵B点下移2米,
∴CD=2米,
在Rt△CED中,已知DE=5米,CD=2米,
则根据勾股定理CE=(米),
∴AE=CE﹣AC=(﹣3)米,
所以梯子底端A将向左滑动(﹣3)米.
16.解:在Rt△ABC中,∠ABC=90°,BC=8m,AC=17m,
∴AB===15(m),
∵工作人员以0.7米/秒的速度拉绳子,经过10秒后游船移动到点D的位置,
∴CD=17﹣0.7×10=10(m),
∴BD===6(m),
∴AD=AB﹣BD=9(m).
答:此时游船移动的距离AD的长是9m.
17.解:由题意得:∠B=90°,
∵BC=8m,BD=6m,
∴CD===10m,
∵AC=17m,
∴绳子移动了AC﹣DC=17﹣10=7(m),用时10秒,
∴工作人员拉绳子的速度是7÷10=0.7米/秒.
18.解:公路AB不需要暂时封锁.
理由如下:如图,过C作CD⊥AB于D.
∵CA⊥CB,
∴∠ACB=90°,
因为BC=800米,AC=600米,
所以,根据勾股定理有AB==1000(米).
因为S△ABC=AB CD=BC AC
所以CD===480(米).
由于400米<480米,故没有危险,
因此AB段公路不需要暂时封锁.
19.解:(1)△ACD是等腰直角三角形.理由如下:
由题意可得:CA=12米,CD=12米,∠CAD=90°,
可得AD===12(米),
故△ACD是等腰直角三角形;
(2)∵CA=12米,CB=20米,∠CAD=90°,
∴AB===16(m),
则BD=AB﹣AD=16﹣12=4(米).
答:船体移动距离BD的长度为4米.
20.解:∵幸福小区C位于快递站点B的北偏东35°方向,沁苑小区D位于B的南偏东55°方向,
∴∠CBA=90°,
∵无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到A需飞行15分钟,
∴BC=8km,BA=15km,
∴由勾股定理得:CA==17(km),
∵无人机以1千米/分钟的速度配送快递,
∴17÷1=17(分钟),
答:从幸福小区C飞到沁苑小区A所需要的时间为17分钟.
1.如图,若圆柱的底面周长是50cm,高是120cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A.170cm B.70cm C.145cm D.130cm
2.如图,学校B前面有一条笔直的公路,学生放学后走AB、BC两条路可到达公路,经测量BC=6km,BA=8km,AC=10km,现需修建一条公路从学校B到公路,则学校B到公路的最短距离为( )
A.4.8km B.9.6km C.2.4km D.5km
3.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20km B.14km C.11km D.10km
4.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.则这只蚂蚁沿着台阶面爬行的最短路程是( )
A.18 B.15 C.12 D.8
5.如图,圆柱的底面直径为,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S,则点P移动的最短距离为 .
6.如图,有一圆柱形油罐,底面周长为24m,高为10m.从A处环绕油罐建梯子,梯子的顶端点B正好在点A的正上方,梯子最短需要 m.
7.已知,如图中未知正方形的面积是 .
8.如图,一圆柱形物体高14cm,底面圆的周长为32cm,在外侧距下底1cm的点S处有一只蜘蛛,与蜘蛛相对的上端外侧距上底1cm的点F处有一只苍蝇,则蜘蛛捕获苍蝇的最短路线长为 cm.
9.如图,一个长方体盒子,BC=CD=8,AB=4,则沿盒子表面从A点到D点的最短路程是 .
10.为响应政府的“公园城市建设”号召,某小区进行小范围绿化,要在一块四边形空地上种植草皮,经测∠B=90°,AB=6米,BC=8米,CD=24米,AD=26米,如果种植草皮费用是300元/米2,那么共需投入多少钱?
11.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有学校,点A到公路MN的距离为120m,现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时130m范围以内都会受到噪音的影响,请你算出该学校受影响的时间多长?
12.如图,一艘轮船以30km/h的速度沿既定航线由西向东航行,途中接到台风警报.某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km.如果这艘轮船不改变航向和速度,那么从接到警报开始,经过多长时间它会进入台风影响区?(结果精确到0.01h,)
13.“新冠肺炎”疫情牵动着14亿中华儿女的心,渠县人民政府积极响应国家号召,及时对广大人民群众进行疫情防控宣传.如图,一笔直公路MN,村庄A到公路MN的距离为600m,若在宣传车P方圆1000m以内能听到广播宣传,那么宣传车P在公路MN上沿MN方向行驶时:
(1)村庄能否听到宣传?请说明理由.
(2)如果能听到,已知宣传车的速度是200m/min,那么村庄总共能听到多长时间的宣传?
14.如图所示,AB=DE=25,AC=24,∠C=90°.
(1)这个梯子底端B离墙有多少米?
(2)如果梯子的顶端下滑的距离AD=4m,求梯子的底部B在水平方向滑动的距离BE的长.
15.如图,一架长为5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC为3米.
(1)求BC的长;
(2)如果梯子的顶端B沿墙向下滑动2米,问梯子的底端向外移动了多少米?
16.位于沈阳周边的红河峡谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A拉回点B的位置(如图).在离水面高度为8m的岸上点C,工作人员用绳子拉船移动,开始时绳子AC的长为17m,工作人员以0.7米/秒的速度拉绳子,经过10秒后游船移动到点D的位置,问此时游船移动的距离AD的长是多少?
17.三水九道谷漂流项目深受欢迎,在景区游船放置区,工作人员把偏离的游船从点A拉回点B的位置(如图).在离水面高度为8m的岸上点C,工作人员用绳子拉船移动,开始时绳子AC的长为17m,经过10秒后游船移动到点D的位置,此时BD=6m,问工作人员拉绳子的速度是多少?
18.在甲村至乙村的公路旁有一块山地需要开发,现有一C处需要爆破,已知点C与公路上的停靠点A的距离为800米,与公路上另一停靠点B的距离为600米,且CA⊥CB,如图,为了安全起见,爆破点C周围半径450米范围内不得进入,问在进行爆破时,公路AB段是否有危险需要暂时封锁?请通过计算进行说明.
19.如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=20米,CA⊥AB且CA=12米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=12米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体移动距离BD的长度.
20.某快递公司为了给客户提供“安全、快速”的优质服务,购置了一台无人机往返A,B,C三地运输货物,如图所示,幸福小区C位于快递站点B的北偏东35°方向,沁苑小区A位于快递站点B的南偏东55°方向,无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到A需飞行15分钟.请求出无人机从幸福小区C飞到沁苑小区A所需要的时间.
参考答案
1.解:如图,圆柱侧面展开图是矩形,
矩形的长为120cm,宽为圆柱的底面周长50cm,
根据勾股定理得:
AB==130(cm),
根据两点之间线段最短,可得丝线的最小长度为130cm,
故选:D.
2.解:过B作BD⊥AC,垂足为D,
∵62+82=102,
∴BC2+AB2=AC2,
∴∠ABC=90°,
∵S△ACB=AB CB=AC BD,
∴×6×8=×10×DB,
解得:BD=4.8,
∴学校B到公路的最短距离为4.8km,
故选:A.
3.解:过点B作BC⊥AC,垂足为C.
观察图形可知AC=AF﹣MF+MC=8﹣3+1=6(km),BC=2+5=7(km),
在Rt△ACB中,AB===10(km).
答:登陆点到宝藏埋藏点的直线距离是10km,
故选:D.
4.解:将台阶展开,如图,
因为AC=3×3+1×3=12,BC=9,
所以AB2=AC2+BC2=225,
所以AB=15,
所以蚂蚁爬行的最短线路为15.
故选:B.
5.解:如图所示,
∵圆柱的底面直径为,BC=12,
∴AB=××π=8,BS=BC=6,
∴AS==10.
故答案为:10.
6.解:将圆柱体的侧面展开,如图所示:
则AC=底面周长=24m,BC=10m,
在Rt△ABC中,AB==26(m),
故答案为:26.
7.解:∵100+125=225=152,
∴“?”所代表的正方形的面积=152=225.
故答案是:225.
8.解:如图展开后连接SF,求出SF的长就是捕获苍蝇充饥的蜘蛛所走的最短路径,
过S作SE⊥CD于E,
则SE=BC=×32=16(cm),
EF=14﹣1﹣1=12(cm),
在Rt△FES中,由勾股定理得:SF===20(cm),
答:捕获苍蝇充饥的蜘蛛所走的最短路径的长度是20cm,
故答案为:20.
9.解:如图,把正面和左面展开,形成一个平面,AD两点之间线段最短.
即AD===4;
如图,把正上面和上面展开,形成一个平面,AD两点之间线段最短.
即AD===4;
如图,把右面和上面展开,形成一个平面,AD两点之间线段最短.
AD==4;
故从A点到D点的最短路程为:4.
故答案为:4.
10.解:连接AC,
∵∠B=90°,
∴在Rt△ABC中,由勾股定理得AC===10(米),
在△ACD中,∵AC2+CD2=102+242=262=AD2,
∴△ACD是直角三角形,且∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD
=AB BC+AC CD
=×6×8+×10×24
=24+120
=144(平方米),
所以需费用300×144=43200(元).
∴需要投入43200元.
11.解:设卡车开到C处刚好开始受到影响,行驶到D处时结束了噪声的影响.
则有CA=DA=130m,
在Rt△ABC中,CB==50(m),
∴CD=2CB=100(m),
则该校受影响的时间为:100÷5=20(s).
答:该学校受影响的时间为20s,
12.解:设x小时后,就进入台风影响区,根据题意得出:
CE=30x千米,BB′=20x千米,
∵BC=500km,AB=300km,
∴AC=400km,
∴AE=400﹣30x,AB′=300﹣20x,
根据勾股定理得:AE2+AB′2=EB′2,
即(400﹣30x)2+(300﹣20x)2=2002,
解得:x1=≈8.35,x2=≈19.3(舍去),
答:轮船经8.35小时就进入台风影响区.
13.解:(1)村庄能听到宣传,理由如下:过点A作AB⊥MN于B,
∵村庄A到公路MN的距离为600米<1000米
∴村庄能听到宣传;
(2)如图:假设当宣讲车行驶到P点开始影响村庄,行驶Q点结束对村庄的影响,
则AP=AQ=1000米,AB=600米,
∴BP=PQ===800(米),
∴PQ=BP+BQ=800+800=1600(米),
∴影响村庄的时间为:1600÷200=8(分钟),
∴村庄总共能听到8分钟的宣传.
14.解:(1)由题意知AB=DE=25米,AC=24米,AD=4米,
在直角△ABC中,∠C=90°,
∴BC2+AC2=AB2,
∴米,
∴这个梯子底端离墙有7米;
(2)已知AD=4米,则CD=24﹣4=20(米),
在直角△CDE中,∠C=90°,
∴BD2+CE2=DE2,
∴(米),
∴BE=15﹣7=8(米),
答:梯子的底部在水平方向滑动了8m.
15.解:(1)∵一架长5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=3米,
∴BC==4(m),
答:BC的长为4m;
(2)∵B点下移2米,
∴CD=2米,
在Rt△CED中,已知DE=5米,CD=2米,
则根据勾股定理CE=(米),
∴AE=CE﹣AC=(﹣3)米,
所以梯子底端A将向左滑动(﹣3)米.
16.解:在Rt△ABC中,∠ABC=90°,BC=8m,AC=17m,
∴AB===15(m),
∵工作人员以0.7米/秒的速度拉绳子,经过10秒后游船移动到点D的位置,
∴CD=17﹣0.7×10=10(m),
∴BD===6(m),
∴AD=AB﹣BD=9(m).
答:此时游船移动的距离AD的长是9m.
17.解:由题意得:∠B=90°,
∵BC=8m,BD=6m,
∴CD===10m,
∵AC=17m,
∴绳子移动了AC﹣DC=17﹣10=7(m),用时10秒,
∴工作人员拉绳子的速度是7÷10=0.7米/秒.
18.解:公路AB不需要暂时封锁.
理由如下:如图,过C作CD⊥AB于D.
∵CA⊥CB,
∴∠ACB=90°,
因为BC=800米,AC=600米,
所以,根据勾股定理有AB==1000(米).
因为S△ABC=AB CD=BC AC
所以CD===480(米).
由于400米<480米,故没有危险,
因此AB段公路不需要暂时封锁.
19.解:(1)△ACD是等腰直角三角形.理由如下:
由题意可得:CA=12米,CD=12米,∠CAD=90°,
可得AD===12(米),
故△ACD是等腰直角三角形;
(2)∵CA=12米,CB=20米,∠CAD=90°,
∴AB===16(m),
则BD=AB﹣AD=16﹣12=4(米).
答:船体移动距离BD的长度为4米.
20.解:∵幸福小区C位于快递站点B的北偏东35°方向,沁苑小区D位于B的南偏东55°方向,
∴∠CBA=90°,
∵无人机以1千米/分钟的速度配送快递时,从B到C需飞行8分钟,从B到A需飞行15分钟,
∴BC=8km,BA=15km,
∴由勾股定理得:CA==17(km),
∵无人机以1千米/分钟的速度配送快递,
∴17÷1=17(分钟),
答:从幸福小区C飞到沁苑小区A所需要的时间为17分钟.
