17.1等腰三角形 同步达标测评 2021-2022学年冀教版八年级数学上册(word版含解析)
文档属性
| 名称 | 17.1等腰三角形 同步达标测评 2021-2022学年冀教版八年级数学上册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 228.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 16:27:07 | ||
图片预览


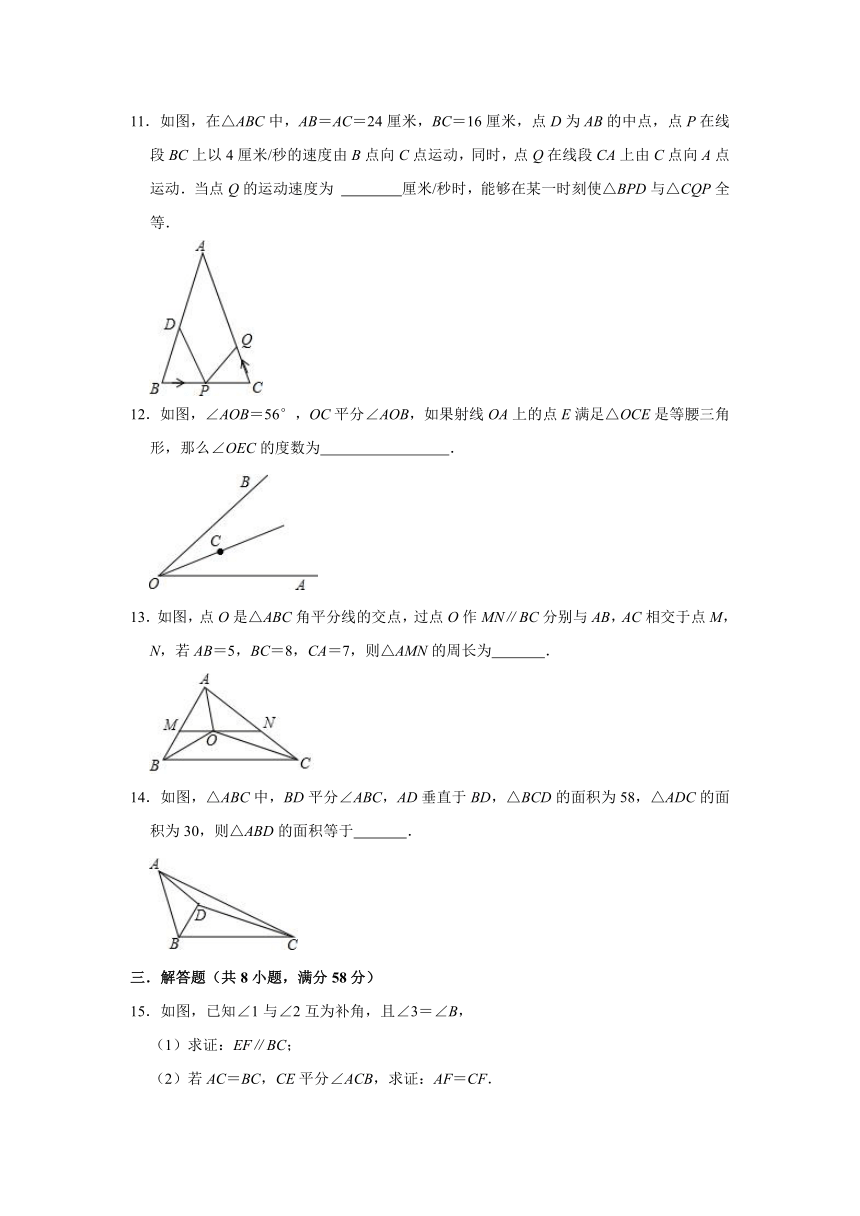


文档简介
2021-2022学年冀教版八年级数学上册《17.1等腰三角形》同步达标测评(附答案)
一.选择题(共8小题,满分32分)
1.如图,在△ABC中,AB=AC,∠A=30°,直线m∥n,顶点C在直线n上,直线m交AB于点D,交AC于点E,若∠1=150°,则∠2的度数是( )
A.45° B.40° C.35° D.30°
2.如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=70°,则∠B等于( )
A.70° B.30° C.40° D.20°
3.等腰三角形的周长是20cm,一边是另一边的两倍,则底边长( )
A.10cm或4cm B.10cm C.4cm D.无法确定
4.如图,在△ABC中,AB=AC,点D,E在边BC上,∠BAD=∠CAE,若BC=15,DE=6,则CE的长为( )
A.3.5 B.4.5 C.5 D.5.5
5.如图,已知△ABC是等腰三角形,AB=AC,点O是BC上任意一点,OE⊥AB,OF⊥AC,等腰三角形的腰长为4,面积为4,则OE+OF的值为( )
A.1.5 B.2 C.2.5 D.3
6.如图,在△ABC中,∠A为钝角,AB=20cm,AC=12cm,点P从点B出发以3cm/s的速度向点A运动,点Q同时从点A出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.当△APQ是等腰三角形时,运动的时间是( )
A.2.5s B.3s C.3.5s D.4s
7.如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论,其中正确的有( )
①△BDF是等腰三角形;②DE=BD+CE;③若∠A=50°,则∠BFC=115°;④DF=EF.
A.1个 B.2个 C.3个 D.4个
8.如图,已知△ABC的面积为12,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是( )
A.10 B.8 C.6 D.4
二.填空题(共6小题,满分30分)
9.等腰△ABC的腰AB边上的中线CD,把△ABC的周长分成12和15两部分,则底边BC长为 .
10.若等腰三角形的顶角为α,则一腰上的高线与另一腰的夹角是 (用α的代数式表示).
11.如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
12.如图,∠AOB=56°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
13.如图,点O是△ABC角平分线的交点,过点O作MN∥BC分别与AB,AC相交于点M,N,若AB=5,BC=8,CA=7,则△AMN的周长为 .
14.如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为58,△ADC的面积为30,则△ABD的面积等于 .
三.解答题(共8小题,满分58分)
15.如图,已知∠1与∠2互为补角,且∠3=∠B,
(1)求证:EF∥BC;
(2)若AC=BC,CE平分∠ACB,求证:AF=CF.
16.如图,在△ABC中,∠BAD=∠C,BE平分∠ABC.
(1)求证:AE=AF;
(2)若AC=BC,∠C=32°,求∠AEF的度数.
17.如图,三角形ABC中,AC=BC,D是BC上的一点,连接AD,DF平分∠ADC交∠ACB的外角∠ACE的平分线于F.
(1)求证:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度数.
18.如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
(1)若∠AFD=155°,求∠EDF的度数;
(2)若点F是AC的中点,求证:∠CFD=∠B.
19.如图所示,在△ABC中,AB=AC,AD平分∠BAC,点G是BA延长线上一点,点F是AC上一点,AG=AF,连接GF并延长交BC于E.
(1)若∠B=55°,求∠AFG的度数;
(2)求证:GE⊥BC.
20.如图,△ABC中,AB=AC,D,E,F分别为AB,BC,CA上的点,且BD=CE,∠DEF=∠B
(1)求证:△BDE≌△CEF;
(2)若∠A=40°,求∠EDF的度数.
21.已知在△ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.
(1)如图1,当点D在边BC的什么位置时,DE=DF?并给出证明;
(2)如图2,过点C作AB边上的高CG,垂足为G,试猜想线段DE,DF,CG的长度之间存在怎样的数量关系?并给出证明.
22.如图所示,已知在△ABC中,AB=AC,D为线段BC上一点,E为线段AC上一点,且AD=AE.
(1)若∠ABC=60°,∠ADE=70°,求∠BAD与∠CDE的度数;
(2)设∠BAD=α,∠CDE=β,试写出α、β之间的关系并加以证明.
参考答案
一.选择题(共8小题,满分32分)
1.解:∵AB=AC,且∠A=30°,
∴∠ACB=75°,
在△ADE中,∵∠1=∠A+∠AED=150°,
∴∠AED=150°﹣30°=120°,
∵m∥n,
∴∠AED=∠2+∠ACB,
∴∠2=120°﹣75°=45°,
故选:A.
2.解:∵CD=CE,
∴∠D=∠CED,
∵∠D=70°,
∴∠C=180°﹣2×70°=40°,
∵AB∥CD,
∴∠B=∠C=40°,
故选:C.
3.解:根据题意设底边长xcm,则腰长为2xcm.
x+2x+2x=20,
解得 x=4
故底边长为4cm,
故选:C.
4.解:∵AB=AC,
∴∠B=∠C,
在△BAD和△CAE中,,
∴△BAD≌△CAE,
∴BD=CE,
∵BC=15,DE=6,
∴BD+CE=9,
∴CE=4.5,
故选:B.
5.解:连接AO,如图,
∵AB=AC=4,
∴S△ABC=S△ABO+S△AOC=AB OE+AC OF=4,
∵AB=AC,
∴AB(OE+OF)=4,
∴OE+OF=2.
故选:B.
6.解:设运动的时间为x,
在△ABC中,AB=20cm,AC=12cm,
点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,
当△APQ是等腰三角形时,AP=AQ,
AP=20﹣3x,AQ=2x
即20﹣3x=2x,
解得x=4.
故选:D.
7.解:∵BF是∠AB的角平分线,
∴∠DBF=∠CBF,
∵DE∥BC,
∴∠DFB=∠CBF,
∴∠DBF=∠DFB,
∴BD=DF,
∴△BDF是等腰三角形;故①正确;
同理,EF=CE,
∴DE=DF+EF=BD+CE,故②正确;
∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵BF平分∠ABC,CF平分∠ACB,
∴,
∴∠FBC+∠FCB=(∠ABC+∠ACB)=65°,
∴∠BFC=180°﹣65°=115°,故③正确;
当△ABC为等腰三角形时,DF=EF,
但△ABC不一定是等腰三角形,
∴DF不一定等于EF,故④错误;
故选:C.
8.解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×12=6,
故选:C.
二.填空题(共6小题,满分30分)
9.解:如图,在△ABC中,AB=AC,且AD=BD.设AB=x,BC=y,
①当AC+AD=15,BD+BC=12时,则x+x=15,x+y=12,
解得x=10,y=7.
②当AC+AD=12,BC+BD=15时,则x+x=12,x+y=15,
解得x=8,y=11,
综上所述,这个三角形的底边BC的长为7或11.
故答案为:7或11.
10.解:当α是锐角时,一腰上的高线与另一腰的夹角是90°﹣α.
当α是钝角时,一腰上的高线与另一腰的夹角是α﹣90°.
当α=90°时,一腰上的高线与另一腰的夹角是0°,
综上所述,等腰三角形的顶角为α,则一腰上的高线与另一腰的夹角是90°﹣α或α﹣90°.
故答案为90°﹣α或α﹣90°.
11.解:设经过x秒后,使△BPD与△CQP全等,
∵AB=AC=24厘米,点D为AB的中点,
∴BD=12厘米,
∵∠ABC=∠ACB,
∴要使△BPD与△CQP全等,必须BD=CP或BP=CP,
即12=16﹣4x或4x=16﹣4x,
解得:x=1或x=2,
x=1时,BP=CQ=4,4÷1=4;
x=2时,BD=CQ=12,12÷2=6;
即点Q的运动速度是4或6,
故答案为:4或6
12.解:∵∠AOB=56°,OC平分∠AOB,
∴∠AOC=28°,
①当E在E1时,OE=CE,
∵∠AOC=∠OCE=28°,
∴∠OEC=180°﹣28°﹣28°=124°;
②当E在E2点时,OC=OE,
则∠OCE=∠OEC=(180°﹣28°)=76°;
③当E在E3时,OC=CE,
则∠OEC=∠AOC=28°;
故答案为:124°或76°或28°.
13.解:∵BO平分∠ABC,
∴∠MBO=∠CBO,
∵MN∥BC,
∴∠MOB=∠CBO,
∴∠MOB=∠MBO,
∴OM=BM,
同理CN=NO,
∴BM+CN=MN,
∴△AMN的周长是AN+MN+AM=AN+CN+OM+ON=AB+AC=5+7=12,
故答案为:12.
14.解:延长AD交BC于E,如图所示:
∵BD平分∠ABC,AD垂直于BD,
∴∠ABD=∠EBD,∠ADB=∠EDB=90°,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(AAS),
∴AD=ED,
∴△ABD的面积=△EBD的面积,△CDE的面积=△ACD的面积=30,
∴△ABD的面积=△EBD的面积=△BCD的面积﹣△CDE的面积=58﹣30=28,
故答案为28.
三.解答题(共8小题,满分58分)
15.(1)证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC.
(2)解:∵EF∥BC,
∴∠BCE=∠FEC,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠FEC=∠ACE.
∴FC=FE,
∵AC=BC,
∴∠A=∠B,
又∵∠B=∠AEF,
∴∠A=∠AEF,
∴AF=FE,
∴AF=CF.
16.(1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠BAD=∠C,
∴∠ABE+∠BAD=∠CBE+∠C,
∵∠AFE=∠ABE+∠BAD,∠AEB=∠CBE+∠C,
∴∠AFE=∠AEB,
∴AE=AF;
(2)解:∵∠C=32°,
∴∠CBA+∠CAB=180°﹣∠C=148°,
∵AC=BC,
∴∠CBA=∠CAB==74°,
∵BE平分∠ABC,
∴∠CBE=ABC=37°,
∴∠AEF=∠C+∠CBE=32°+37°=69°.
17.(1)证明:∵AC=BC,
∴∠ABC=∠CAB,
∴∠ACE=∠ABC+∠CAB=2∠ABC
∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE
∴2∠ABC=2∠FCE,
∴∠ABC=∠FCE,
∴CF∥AB;
(2)∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE=∠ADC+∠DAC
∵DF平分∠ADC,
∴∠ADC=2∠FDC;
∴2∠FCE=∠ADC+∠DAC=2∠FDC+∠DAC,
∴2∠FCE﹣2∠FDC=∠DAC
∵∠DFC=∠FCE﹣∠FDC
∴2∠DFC=2∠FCE﹣2∠FDC=∠DAC=40°
∴∠DFC=20°.
18.解:(1)∵∠AFD=155°,
∴∠DFC=25°,
∵DF⊥BC,DE⊥AB,
∴∠FDC=∠AED=90°,
在Rt△FDC中,
∴∠C=90°﹣25°=65°,
∵AB=BC,
∴∠C=∠A=65°,
∴∠EDF=360°﹣65°﹣155°﹣90°=50°.
(2)连接BF
∵AB=BC,且点F是AC的中点,
∴BF⊥AC,∠ABF=∠CBF=∠ABC,
∴∠CFD+∠BFD=90°,
∠CBF+∠BFD=90°,
∴∠CFD=∠CBF,
∴∠CFD=∠ABC.
19.(1)解:∵AB=AC,
∴∠B=∠C=55°,
∴∠GAF=∠B+∠C=110°,
∵AG=AF,
∴∠AFG=(180°﹣110°)=35°.
(2)证明:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°
∴∠BAD=∠CAD=90°﹣55°=35°,
∴∠DAC=∠AFG,
∴AD∥FG,
∴GE⊥BC.
20.(1)证明:∵∠DEC=∠B+∠BDE=∠CEF+∠DEF,∠DEF=∠B,
∴∠CEF=∠BDE.
∵AB=AC,
∴∠C=∠B.
又∵CE=BD,
∴△BDE≌△CEF.
(2)解:∵△BDE≌△CEF
∴DE=FE.
所以△DEF是等腰三角形.
∴∠EDF=∠EFD
又,△ABC中,AB=AC,∠A=40°
∴∠B=70°,
已知∠DEF=∠B
∴∠DEF=70°
∴∠EDF=∠EFD=×(180°﹣70°)=55°.
21.解:(1)当点D在BC的中点上时,DE=DF,
证明:∵D为BC中点,
∴BD=CD,
∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF.
(2)CG=DE+DF
证明:连接AD,
∵S三角形ABC=S三角形ADB+S三角形ADC,
∴AB×CG=AB×DE+AC×DF,
∵AB=AC,
∴CG=DE+DF.
22.解:(1)∵AB=AC,
∴∠B=∠C=60°,
∴∠BAC=60°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠DAE=40°,
∴∠BAD=∠BAC﹣∠DAE=20°,
∵∠AED=∠CDE+∠C,
∴∠CDE=70°﹣60°=10°.
(2)结论:α=2β,理由是:
设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,
∵∠ACB=∠ABC,
∴∠ACB=,
∵∠ADE=∠AED,
∴∠AED=,
∴β=∠AED﹣∠ACB=﹣==,
∴α=2β;
一.选择题(共8小题,满分32分)
1.如图,在△ABC中,AB=AC,∠A=30°,直线m∥n,顶点C在直线n上,直线m交AB于点D,交AC于点E,若∠1=150°,则∠2的度数是( )
A.45° B.40° C.35° D.30°
2.如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=70°,则∠B等于( )
A.70° B.30° C.40° D.20°
3.等腰三角形的周长是20cm,一边是另一边的两倍,则底边长( )
A.10cm或4cm B.10cm C.4cm D.无法确定
4.如图,在△ABC中,AB=AC,点D,E在边BC上,∠BAD=∠CAE,若BC=15,DE=6,则CE的长为( )
A.3.5 B.4.5 C.5 D.5.5
5.如图,已知△ABC是等腰三角形,AB=AC,点O是BC上任意一点,OE⊥AB,OF⊥AC,等腰三角形的腰长为4,面积为4,则OE+OF的值为( )
A.1.5 B.2 C.2.5 D.3
6.如图,在△ABC中,∠A为钝角,AB=20cm,AC=12cm,点P从点B出发以3cm/s的速度向点A运动,点Q同时从点A出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.当△APQ是等腰三角形时,运动的时间是( )
A.2.5s B.3s C.3.5s D.4s
7.如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论,其中正确的有( )
①△BDF是等腰三角形;②DE=BD+CE;③若∠A=50°,则∠BFC=115°;④DF=EF.
A.1个 B.2个 C.3个 D.4个
8.如图,已知△ABC的面积为12,BP平分∠ABC,且AP⊥BP于点P,则△BPC的面积是( )
A.10 B.8 C.6 D.4
二.填空题(共6小题,满分30分)
9.等腰△ABC的腰AB边上的中线CD,把△ABC的周长分成12和15两部分,则底边BC长为 .
10.若等腰三角形的顶角为α,则一腰上的高线与另一腰的夹角是 (用α的代数式表示).
11.如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
12.如图,∠AOB=56°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
13.如图,点O是△ABC角平分线的交点,过点O作MN∥BC分别与AB,AC相交于点M,N,若AB=5,BC=8,CA=7,则△AMN的周长为 .
14.如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为58,△ADC的面积为30,则△ABD的面积等于 .
三.解答题(共8小题,满分58分)
15.如图,已知∠1与∠2互为补角,且∠3=∠B,
(1)求证:EF∥BC;
(2)若AC=BC,CE平分∠ACB,求证:AF=CF.
16.如图,在△ABC中,∠BAD=∠C,BE平分∠ABC.
(1)求证:AE=AF;
(2)若AC=BC,∠C=32°,求∠AEF的度数.
17.如图,三角形ABC中,AC=BC,D是BC上的一点,连接AD,DF平分∠ADC交∠ACB的外角∠ACE的平分线于F.
(1)求证:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度数.
18.如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
(1)若∠AFD=155°,求∠EDF的度数;
(2)若点F是AC的中点,求证:∠CFD=∠B.
19.如图所示,在△ABC中,AB=AC,AD平分∠BAC,点G是BA延长线上一点,点F是AC上一点,AG=AF,连接GF并延长交BC于E.
(1)若∠B=55°,求∠AFG的度数;
(2)求证:GE⊥BC.
20.如图,△ABC中,AB=AC,D,E,F分别为AB,BC,CA上的点,且BD=CE,∠DEF=∠B
(1)求证:△BDE≌△CEF;
(2)若∠A=40°,求∠EDF的度数.
21.已知在△ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.
(1)如图1,当点D在边BC的什么位置时,DE=DF?并给出证明;
(2)如图2,过点C作AB边上的高CG,垂足为G,试猜想线段DE,DF,CG的长度之间存在怎样的数量关系?并给出证明.
22.如图所示,已知在△ABC中,AB=AC,D为线段BC上一点,E为线段AC上一点,且AD=AE.
(1)若∠ABC=60°,∠ADE=70°,求∠BAD与∠CDE的度数;
(2)设∠BAD=α,∠CDE=β,试写出α、β之间的关系并加以证明.
参考答案
一.选择题(共8小题,满分32分)
1.解:∵AB=AC,且∠A=30°,
∴∠ACB=75°,
在△ADE中,∵∠1=∠A+∠AED=150°,
∴∠AED=150°﹣30°=120°,
∵m∥n,
∴∠AED=∠2+∠ACB,
∴∠2=120°﹣75°=45°,
故选:A.
2.解:∵CD=CE,
∴∠D=∠CED,
∵∠D=70°,
∴∠C=180°﹣2×70°=40°,
∵AB∥CD,
∴∠B=∠C=40°,
故选:C.
3.解:根据题意设底边长xcm,则腰长为2xcm.
x+2x+2x=20,
解得 x=4
故底边长为4cm,
故选:C.
4.解:∵AB=AC,
∴∠B=∠C,
在△BAD和△CAE中,,
∴△BAD≌△CAE,
∴BD=CE,
∵BC=15,DE=6,
∴BD+CE=9,
∴CE=4.5,
故选:B.
5.解:连接AO,如图,
∵AB=AC=4,
∴S△ABC=S△ABO+S△AOC=AB OE+AC OF=4,
∵AB=AC,
∴AB(OE+OF)=4,
∴OE+OF=2.
故选:B.
6.解:设运动的时间为x,
在△ABC中,AB=20cm,AC=12cm,
点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,
当△APQ是等腰三角形时,AP=AQ,
AP=20﹣3x,AQ=2x
即20﹣3x=2x,
解得x=4.
故选:D.
7.解:∵BF是∠AB的角平分线,
∴∠DBF=∠CBF,
∵DE∥BC,
∴∠DFB=∠CBF,
∴∠DBF=∠DFB,
∴BD=DF,
∴△BDF是等腰三角形;故①正确;
同理,EF=CE,
∴DE=DF+EF=BD+CE,故②正确;
∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵BF平分∠ABC,CF平分∠ACB,
∴,
∴∠FBC+∠FCB=(∠ABC+∠ACB)=65°,
∴∠BFC=180°﹣65°=115°,故③正确;
当△ABC为等腰三角形时,DF=EF,
但△ABC不一定是等腰三角形,
∴DF不一定等于EF,故④错误;
故选:C.
8.解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,
,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×12=6,
故选:C.
二.填空题(共6小题,满分30分)
9.解:如图,在△ABC中,AB=AC,且AD=BD.设AB=x,BC=y,
①当AC+AD=15,BD+BC=12时,则x+x=15,x+y=12,
解得x=10,y=7.
②当AC+AD=12,BC+BD=15时,则x+x=12,x+y=15,
解得x=8,y=11,
综上所述,这个三角形的底边BC的长为7或11.
故答案为:7或11.
10.解:当α是锐角时,一腰上的高线与另一腰的夹角是90°﹣α.
当α是钝角时,一腰上的高线与另一腰的夹角是α﹣90°.
当α=90°时,一腰上的高线与另一腰的夹角是0°,
综上所述,等腰三角形的顶角为α,则一腰上的高线与另一腰的夹角是90°﹣α或α﹣90°.
故答案为90°﹣α或α﹣90°.
11.解:设经过x秒后,使△BPD与△CQP全等,
∵AB=AC=24厘米,点D为AB的中点,
∴BD=12厘米,
∵∠ABC=∠ACB,
∴要使△BPD与△CQP全等,必须BD=CP或BP=CP,
即12=16﹣4x或4x=16﹣4x,
解得:x=1或x=2,
x=1时,BP=CQ=4,4÷1=4;
x=2时,BD=CQ=12,12÷2=6;
即点Q的运动速度是4或6,
故答案为:4或6
12.解:∵∠AOB=56°,OC平分∠AOB,
∴∠AOC=28°,
①当E在E1时,OE=CE,
∵∠AOC=∠OCE=28°,
∴∠OEC=180°﹣28°﹣28°=124°;
②当E在E2点时,OC=OE,
则∠OCE=∠OEC=(180°﹣28°)=76°;
③当E在E3时,OC=CE,
则∠OEC=∠AOC=28°;
故答案为:124°或76°或28°.
13.解:∵BO平分∠ABC,
∴∠MBO=∠CBO,
∵MN∥BC,
∴∠MOB=∠CBO,
∴∠MOB=∠MBO,
∴OM=BM,
同理CN=NO,
∴BM+CN=MN,
∴△AMN的周长是AN+MN+AM=AN+CN+OM+ON=AB+AC=5+7=12,
故答案为:12.
14.解:延长AD交BC于E,如图所示:
∵BD平分∠ABC,AD垂直于BD,
∴∠ABD=∠EBD,∠ADB=∠EDB=90°,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(AAS),
∴AD=ED,
∴△ABD的面积=△EBD的面积,△CDE的面积=△ACD的面积=30,
∴△ABD的面积=△EBD的面积=△BCD的面积﹣△CDE的面积=58﹣30=28,
故答案为28.
三.解答题(共8小题,满分58分)
15.(1)证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC.
(2)解:∵EF∥BC,
∴∠BCE=∠FEC,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠FEC=∠ACE.
∴FC=FE,
∵AC=BC,
∴∠A=∠B,
又∵∠B=∠AEF,
∴∠A=∠AEF,
∴AF=FE,
∴AF=CF.
16.(1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠BAD=∠C,
∴∠ABE+∠BAD=∠CBE+∠C,
∵∠AFE=∠ABE+∠BAD,∠AEB=∠CBE+∠C,
∴∠AFE=∠AEB,
∴AE=AF;
(2)解:∵∠C=32°,
∴∠CBA+∠CAB=180°﹣∠C=148°,
∵AC=BC,
∴∠CBA=∠CAB==74°,
∵BE平分∠ABC,
∴∠CBE=ABC=37°,
∴∠AEF=∠C+∠CBE=32°+37°=69°.
17.(1)证明:∵AC=BC,
∴∠ABC=∠CAB,
∴∠ACE=∠ABC+∠CAB=2∠ABC
∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE
∴2∠ABC=2∠FCE,
∴∠ABC=∠FCE,
∴CF∥AB;
(2)∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE=∠ADC+∠DAC
∵DF平分∠ADC,
∴∠ADC=2∠FDC;
∴2∠FCE=∠ADC+∠DAC=2∠FDC+∠DAC,
∴2∠FCE﹣2∠FDC=∠DAC
∵∠DFC=∠FCE﹣∠FDC
∴2∠DFC=2∠FCE﹣2∠FDC=∠DAC=40°
∴∠DFC=20°.
18.解:(1)∵∠AFD=155°,
∴∠DFC=25°,
∵DF⊥BC,DE⊥AB,
∴∠FDC=∠AED=90°,
在Rt△FDC中,
∴∠C=90°﹣25°=65°,
∵AB=BC,
∴∠C=∠A=65°,
∴∠EDF=360°﹣65°﹣155°﹣90°=50°.
(2)连接BF
∵AB=BC,且点F是AC的中点,
∴BF⊥AC,∠ABF=∠CBF=∠ABC,
∴∠CFD+∠BFD=90°,
∠CBF+∠BFD=90°,
∴∠CFD=∠CBF,
∴∠CFD=∠ABC.
19.(1)解:∵AB=AC,
∴∠B=∠C=55°,
∴∠GAF=∠B+∠C=110°,
∵AG=AF,
∴∠AFG=(180°﹣110°)=35°.
(2)证明:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°
∴∠BAD=∠CAD=90°﹣55°=35°,
∴∠DAC=∠AFG,
∴AD∥FG,
∴GE⊥BC.
20.(1)证明:∵∠DEC=∠B+∠BDE=∠CEF+∠DEF,∠DEF=∠B,
∴∠CEF=∠BDE.
∵AB=AC,
∴∠C=∠B.
又∵CE=BD,
∴△BDE≌△CEF.
(2)解:∵△BDE≌△CEF
∴DE=FE.
所以△DEF是等腰三角形.
∴∠EDF=∠EFD
又,△ABC中,AB=AC,∠A=40°
∴∠B=70°,
已知∠DEF=∠B
∴∠DEF=70°
∴∠EDF=∠EFD=×(180°﹣70°)=55°.
21.解:(1)当点D在BC的中点上时,DE=DF,
证明:∵D为BC中点,
∴BD=CD,
∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF.
(2)CG=DE+DF
证明:连接AD,
∵S三角形ABC=S三角形ADB+S三角形ADC,
∴AB×CG=AB×DE+AC×DF,
∵AB=AC,
∴CG=DE+DF.
22.解:(1)∵AB=AC,
∴∠B=∠C=60°,
∴∠BAC=60°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠DAE=40°,
∴∠BAD=∠BAC﹣∠DAE=20°,
∵∠AED=∠CDE+∠C,
∴∠CDE=70°﹣60°=10°.
(2)结论:α=2β,理由是:
设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,
∵∠ACB=∠ABC,
∴∠ACB=,
∵∠ADE=∠AED,
∴∠AED=,
∴β=∠AED﹣∠ACB=﹣==,
∴α=2β;
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
