2021-2022学年人教版九年级数学下册26.1.2.1反比例函数的图象和性质同步练习(word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册26.1.2.1反比例函数的图象和性质同步练习(word版、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 242.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 15:09:11 | ||
图片预览


文档简介
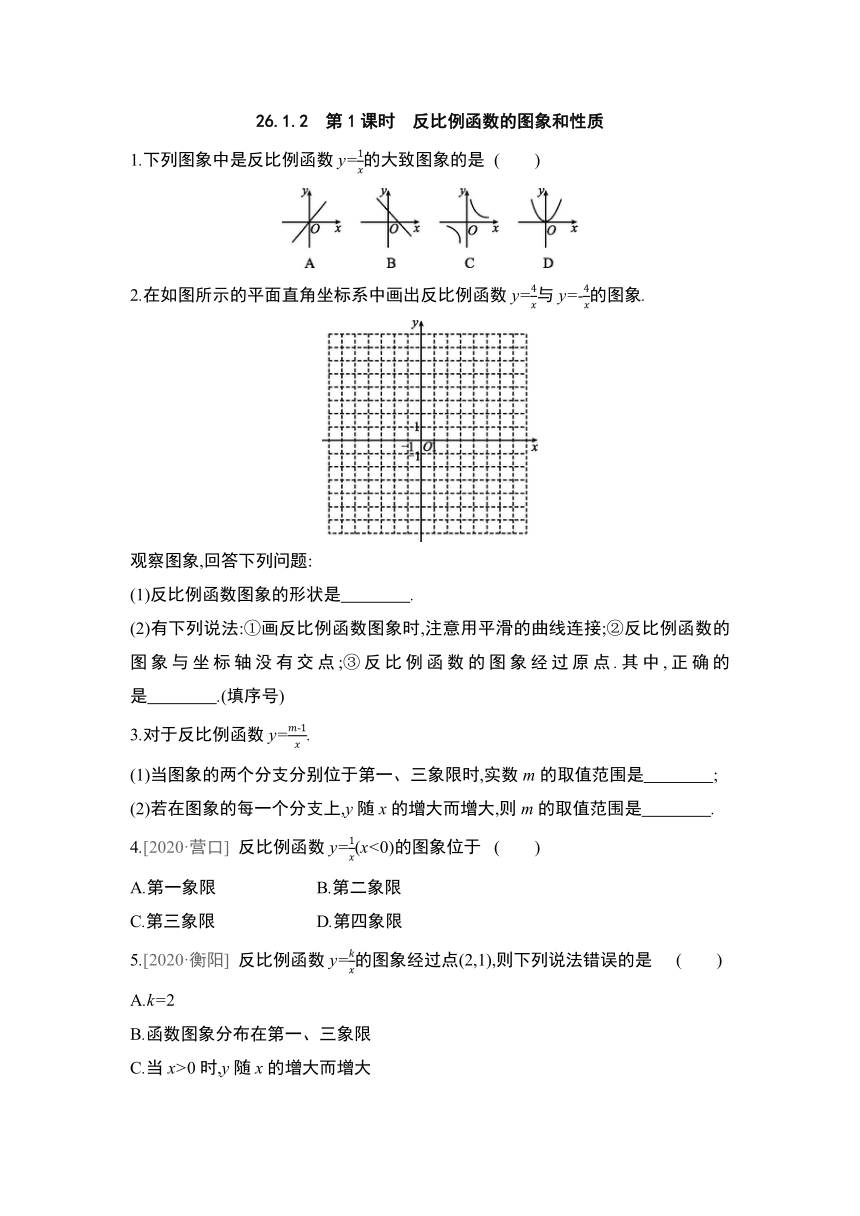
26.1.2 第1课时 反比例函数的图象和性质
1.下列图象中是反比例函数y=的大致图象的是 ( )
2.在如图所示的平面直角坐标系中画出反比例函数y=与y=-的图象.
观察图象,回答下列问题:
(1)反比例函数图象的形状是 .
(2)有下列说法:①画反比例函数图象时,注意用平滑的曲线连接;②反比例函数的图象与坐标轴没有交点;③反比例函数的图象经过原点.其中,正确的是 .(填序号)
3.对于反比例函数y=.
(1)当图象的两个分支分别位于第一、三象限时,实数m的取值范围是 ;
(2)若在图象的每一个分支上,y随x的增大而增大,则m的取值范围是 .
4.[2020·营口] 反比例函数y=(x<0)的图象位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.[2020·衡阳] 反比例函数y=的图象经过点(2,1),则下列说法错误的是 ( )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,y随x的增大而减小
6.[2020·河南] 若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y=-的图象上,则y1,y2,y3的大小关系是 ( )
A.y1>y2>y3 B.y2>y3>y1
C.y1>y3>y2 D.y3>y2>y1
7.反比例函数y=的图象如图,则函数y=-kx+2的图象可能是图中的 ( )
8.已知点A(x1,3),B(x2,6)都在反比例函数y=-的图象上,则下列关系式一定正确的是 ( )
A.x1C.x29.[2020·桂林] 反比例函数y=(x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=-x对称;④若点(-2,3)在该反比例函数的图象上,则点(-1,6)也在该函数的图象上.其中正确的结论有 个.
10.在如图所示的平面直角坐标系中,作出函数y=的图象,并根据图象回答下列问题:
(1)当x=-2时,求y的值;
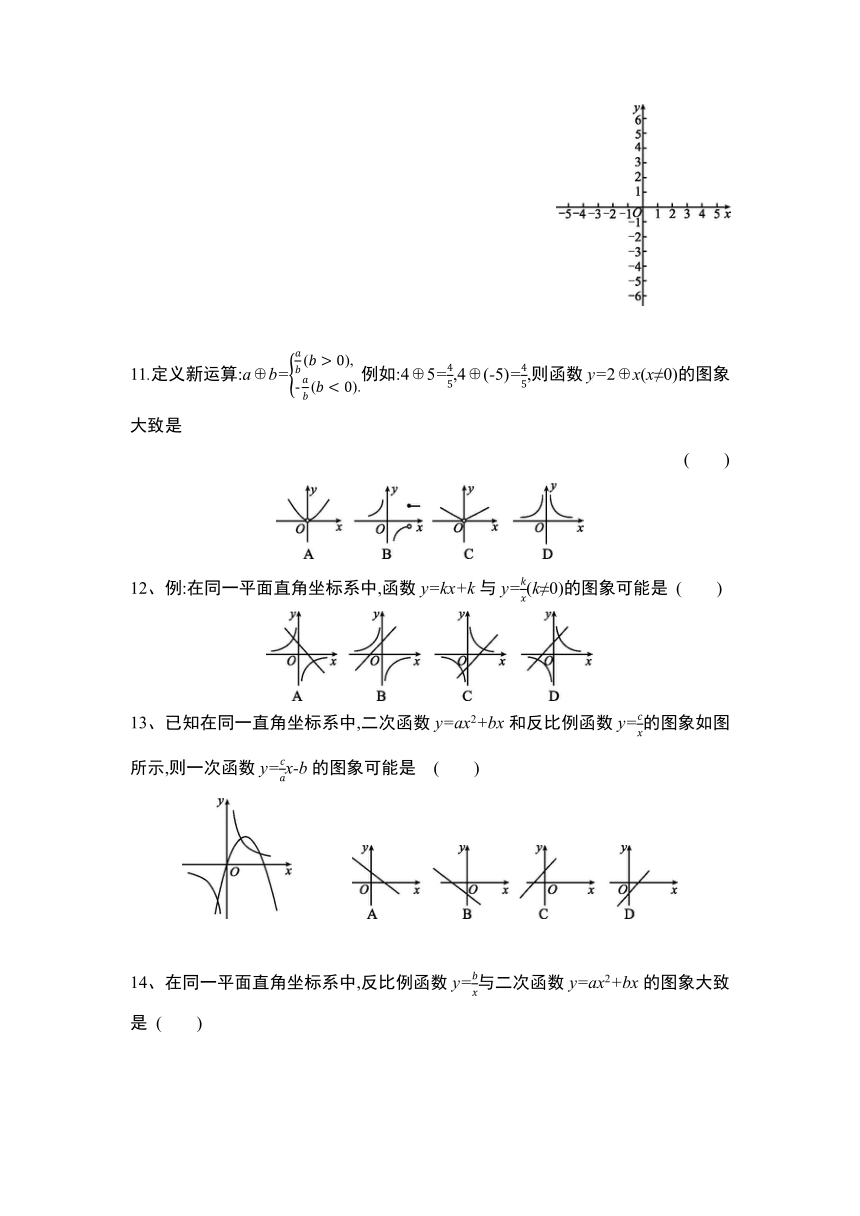
(2)当2(3)当-111.定义新运算:a b=例如:4 5=,4 (-5)=,则函数y=2 x(x≠0)的图象大致是
( )
12、例:在同一平面直角坐标系中,函数y=kx+k与y=(k≠0)的图象可能是 ( )
13、已知在同一直角坐标系中,二次函数y=ax2+bx和反比例函数y=的图象如图所示,则一次函数y=x-b的图象可能是 ( )
14、在同一平面直角坐标系中,反比例函数y=与二次函数y=ax2+bx的图象大致是 ( )
15、如图,已知反比例函数y=的图象经过点A(1,3),B(3,m).
(1)求反比例函数的解析式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
1.C
2.画图略 (1)双曲线 (2)①②
3.(1)m>1 (2)m<1
4.C 5.C 6.C
7.B 因为反比例函数y=的图象分布在第二、四象限,所以k<0,则-k>0,
所以函数y=-kx+2的图象可能如图: 故选B.
8.A 因为点A(x1,3),B(x2,6)都在反比例函数y=-的图象上,所以x1=-1,x2=-.因为-1<-<0,所以x19.3
10.解:如图所示.
(1)当x=-2时,y=-3. (2)当23.
11.D 由题意可知:当x>0时,函数y=2 x可化为y=;当x<0时,函数y=2 x可化为y=-.当x>0时,反比例函数y=的图象在第一象限,当x<0时,反比例函数y=-的图象在第二象限.故选D.
12、D ①当k>0时,函数y=kx+k的图象过第一、二、三象限;函数y=的图象过第一、三象限;②当k<0时,函数y=kx+k的图象过第二、三、四象限;函数y=的图象过第二、四象限.观察图形可知,只有D选项符合题意.故选D.
13、B
14、D
15.解:(1)把点A(1,3)的坐标代入y=,得k=1×3=3,所以反比例函数的解析式为y=.
把点B(3,m)的坐标代入y=,得m=,解得m=1,所以点B的坐标为(3,1).
(2)如图,作点A关于x轴的对称点A',则A'(1,-3),连接BA'交x轴于点P,此时PA+PB的值最小.
设直线BA'的函数解析式为y=ax+b.把点A'(1,-3),B(3,1)的坐标分别代入y=ax+b,得解得所以直线BA'的函数解析式为y=2x-5.当y=0时,2x-5=0,解得x=,
所以点P的坐标为,0.
1.下列图象中是反比例函数y=的大致图象的是 ( )
2.在如图所示的平面直角坐标系中画出反比例函数y=与y=-的图象.
观察图象,回答下列问题:
(1)反比例函数图象的形状是 .
(2)有下列说法:①画反比例函数图象时,注意用平滑的曲线连接;②反比例函数的图象与坐标轴没有交点;③反比例函数的图象经过原点.其中,正确的是 .(填序号)
3.对于反比例函数y=.
(1)当图象的两个分支分别位于第一、三象限时,实数m的取值范围是 ;
(2)若在图象的每一个分支上,y随x的增大而增大,则m的取值范围是 .
4.[2020·营口] 反比例函数y=(x<0)的图象位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.[2020·衡阳] 反比例函数y=的图象经过点(2,1),则下列说法错误的是 ( )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,y随x的增大而减小
6.[2020·河南] 若点A(-1,y1),B(2,y2),C(3,y3)在反比例函数y=-的图象上,则y1,y2,y3的大小关系是 ( )
A.y1>y2>y3 B.y2>y3>y1
C.y1>y3>y2 D.y3>y2>y1
7.反比例函数y=的图象如图,则函数y=-kx+2的图象可能是图中的 ( )
8.已知点A(x1,3),B(x2,6)都在反比例函数y=-的图象上,则下列关系式一定正确的是 ( )
A.x1
10.在如图所示的平面直角坐标系中,作出函数y=的图象,并根据图象回答下列问题:
(1)当x=-2时,求y的值;
(2)当2
( )
12、例:在同一平面直角坐标系中,函数y=kx+k与y=(k≠0)的图象可能是 ( )
13、已知在同一直角坐标系中,二次函数y=ax2+bx和反比例函数y=的图象如图所示,则一次函数y=x-b的图象可能是 ( )
14、在同一平面直角坐标系中,反比例函数y=与二次函数y=ax2+bx的图象大致是 ( )
15、如图,已知反比例函数y=的图象经过点A(1,3),B(3,m).
(1)求反比例函数的解析式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
1.C
2.画图略 (1)双曲线 (2)①②
3.(1)m>1 (2)m<1
4.C 5.C 6.C
7.B 因为反比例函数y=的图象分布在第二、四象限,所以k<0,则-k>0,
所以函数y=-kx+2的图象可能如图: 故选B.
8.A 因为点A(x1,3),B(x2,6)都在反比例函数y=-的图象上,所以x1=-1,x2=-.因为-1<-<0,所以x1
10.解:如图所示.
(1)当x=-2时,y=-3. (2)当2
11.D 由题意可知:当x>0时,函数y=2 x可化为y=;当x<0时,函数y=2 x可化为y=-.当x>0时,反比例函数y=的图象在第一象限,当x<0时,反比例函数y=-的图象在第二象限.故选D.
12、D ①当k>0时,函数y=kx+k的图象过第一、二、三象限;函数y=的图象过第一、三象限;②当k<0时,函数y=kx+k的图象过第二、三、四象限;函数y=的图象过第二、四象限.观察图形可知,只有D选项符合题意.故选D.
13、B
14、D
15.解:(1)把点A(1,3)的坐标代入y=,得k=1×3=3,所以反比例函数的解析式为y=.
把点B(3,m)的坐标代入y=,得m=,解得m=1,所以点B的坐标为(3,1).
(2)如图,作点A关于x轴的对称点A',则A'(1,-3),连接BA'交x轴于点P,此时PA+PB的值最小.
设直线BA'的函数解析式为y=ax+b.把点A'(1,-3),B(3,1)的坐标分别代入y=ax+b,得解得所以直线BA'的函数解析式为y=2x-5.当y=0时,2x-5=0,解得x=,
所以点P的坐标为,0.
