人教版 三年级下册数学 7、 小数的初步认识 练习二十一 课件 (共33张PPT)
文档属性
| 名称 | 人教版 三年级下册数学 7、 小数的初步认识 练习二十一 课件 (共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 10:08:01 | ||
图片预览










文档简介
(共33张PPT)
人教版数学三年级(下)
练习二十一
7
小数的初步认识
重点回顾
列竖式计算小数加、减法的方法是什么?
1.相同数位对齐(小数点对齐)。
2.按整数加减法的方法计算。
3.得数小数点要和加数、减数或被减数对齐。
解决小数加、减法的实际问题过程中,你发现了什么?
解决小数加、减法的实际问题的步骤
1.先明确所求问题是什么。
2.根据这个问题,整理信息。
3.分析题意并列出算式,然后进行计算。
解决小数加、减法的实际问题过程中,你发现了什么?
1. 在解决有关小数的加、减法问题时,可以从不同的角度思考,选择不同的解题方法。
2.解决问题的不同方法可以互相检验。
2.3
0.8
3.9
1.
练习巩固
+ =
4.5
1.4
6.2
6.8
2.2
10.1
=
2.7
4.1
8.4
1.5
0.3
7.5
1.2
3.8
0.9
列竖式计算时,注意小数点要对齐。
(教材第98~100页练习二十一)
2.
(1)《动脑筋》比《童话故事选》便宜多少元?
6.8元
3.4元
6.8-3.4=
3.4(元)
3.4
6.8
3.4
-
答:《动脑筋》比《童话故事选》便宜3.4元。
也就是求3.4和6.8的和,用减法计算,列式为6.8-3.4。
可以先算出一共花了多少钱,再跟10元比较。
6.8+3.4=
10.2(元)
答:各买1本书,10元钱不够。
10.2>10
2.
6.8元
3.4元
(2)各买1本书,10元钱够不够?
3.计算下面各题。
2.1
+
4.8
6
9
.
1.5
+
7.5
9
0
.
1
8.7
6.3
2
4
.
10.0
3.6
6
4
.
.
3.2
1.7
1
5
.
14.6
+
5.7
0
3
.
1
.
2
1
31.8
17.2
4
6
.
1
.
20.7
+
14.9
5
6
.
3
1
.
先把小数点对齐,再按照整数加、减法的法则进行计算,得数里的小数点要和横线上的小数点对齐。
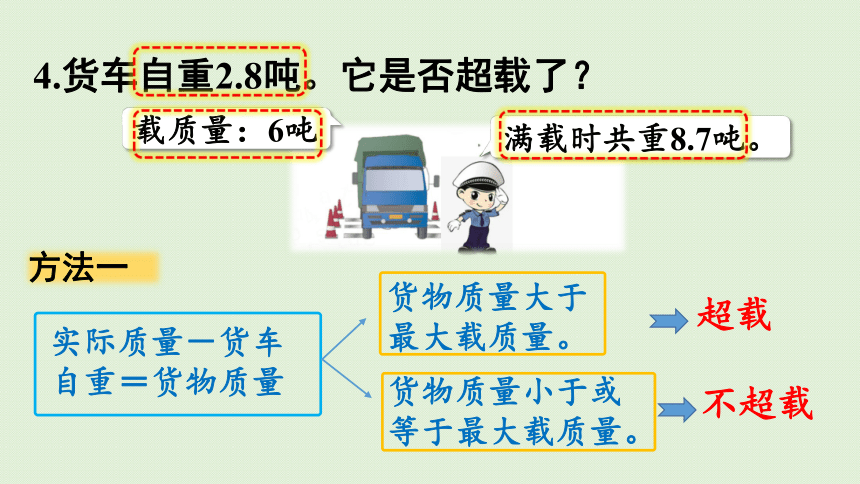
实际质量-货车自重=货物质量
货物质量大于最大载质量。
货物质量小于或等于最大载质量。
超载
不超载
4.货车自重2.8吨。它是否超载了?
满载时共重8.7吨。
载质量:6吨
方法一
8.7-2.8=5.9(吨)
5.9吨<6吨
答:它没有超载。
4.货车自重2.8吨。它是否超载了?
满载时共重8.7吨。
载质量:6吨
方法一
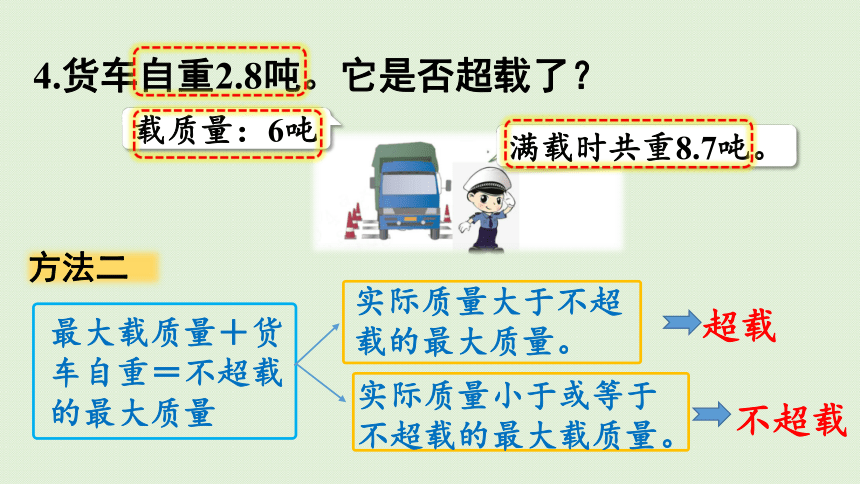
最大载质量+货车自重=不超载的最大质量
实际质量大于不超载的最大质量。
实际质量小于或等于不超载的最大载质量。
超载
不超载
4.货车自重2.8吨。它是否超载了?
满载时共重8.7吨。
载质量:6吨
方法二
6+2.8=8.8(吨)
8.8吨>8.7吨
答:它没有超载。
4.货车自重2.8吨。它是否超载了?
满载时共重8.7吨。
载质量:6吨
方法二
5.根据图中的涂色部分写出小数,再比较大小。
( ) ( )
>
( ) ( )
<
0.7
0.5
0.9
1.2
把一个整体平均分成10份,每份0.1,几份也就十分之几,零点几。
6.
(1)哪种玩具最贵?最贵的比最便宜的玩具贵多少钱?
最贵
最便宜
7.1-0.8=6.3(元)
答:机器人最贵,最贵的比最便宜的玩具贵6.3元。
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
观察这些价格,整数部分都不相同,直接比较整数部分即可。
6.
(2)挑选两个你最喜欢的玩具,需要多少钱?
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
答案不唯一,例如:
5.5+3.7=9.2(元)
答:需要9.2元。
6.
(3)小东有10元,买一个 后,还可以买哪两个玩具?
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
先算出剩余钱数,所买玩具总和不超过剩余钱数即可。
6.
(3)小东有10元,买一个 后,还可以买哪两个玩具?
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
答案不唯一,例如:
10-5.5=4.5(元)
买喇叭和魔方:
0.8+3.7=4.5(元)
6.
(4)你还能提出一个数学问题并解答吗?
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
答案不唯一,例如:
买一个玩具熊和1个皮球一共多少钱?
4.3+1.6=5.9(元)
答:一共5.9元。
7.小丽从儿童乐园上车,要到光明街站下车。如果每两站间相距为1千米,小丽要付车费多少钱
坐10站或10站以内都只要1元。
1
2
超过10站,每站增加0.2元。
到光明站下车共坐12站,用连加计算。
1+0.2+0.2=1.4(元)
答:小丽要付车费1.4元。
7.小丽从儿童乐园上车,要到光明街站下车。如果每两站间相距为1千米,小丽要付车费多少钱
(1)长颈鹿现在能上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
方法一
先算犀牛和长颈鹿的总重。
小于或等于4吨,可以过桥。
大于4吨,不能过桥。
再跟限重4吨比较。
(1)长颈鹿现在能上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
方法一
2.7+1.5=4.2(吨)
4.2吨>4吨
答:长颈鹿现在不能上桥。
(1)长颈鹿现在能上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
方法二
先算犀牛上桥后剩余最大限重。
小于或等于长颈鹿的体重,不可以过桥。
大于长颈鹿的体重,可以过桥。
再跟长颈鹿的体重比较。
(1)长颈鹿现在能上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
方法二
4-2.7=1.3(吨)
1.3吨<1.5吨
答:长颈鹿现在不能上桥。
(2)棕熊现在能上桥吗?斑马可以和它一起上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
先算犀牛上桥后剩余最大限重。
将棕熊体重跟剩余最大限重比较,大于剩余部分,不可以,小于或等于剩余部分,可以。
将棕熊和斑马的体重和跟剩余最大限重比较,大于剩余部分,不可以,小于或等于剩余部分,可以。
(2)棕熊现在能上桥吗?斑马可以和它一起上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
4-2.7=1.3(吨) 0.8吨<1.3吨
0.8+0.3=1.1(吨)1.1吨<1.3吨
答:棕熊现在能上桥,斑马可以和它一起上桥。
(3)你还能提出其他数学问题并解答吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
长颈鹿和棕熊可以一起过桥吗?
1.5+0.8=2.3(吨) 2.3吨<4吨
答:长颈鹿和棕熊可以一起过桥。
答案不唯一
9.
3个城市城镇居民人均住房使用面积如下表。你能提出哪些问题?你会解答提出的问题吗?
城市 A B C
面积/平方米 14.6 16.7 17.6
本题可以提出相关的加法或减法解决的问题。
17.6 16.7=0.9(平方米)
例如:B市城镇居民人均住房使用面积比C市少多少平方米?
答:少0.9平方米。
9.
3个城市城镇居民人均住房使用面积如下表。你能提出哪些问题?你会解答提出的问题吗?
城市 A B C
面积/平方米 14.6 16.7 17.6
10.
按规律接着往下写。
(1)1.1, 1.2, 1.3, 1.4, 1.5,( ),( ),
( )。
1.6
(2) 0.6,1.2, 1.8, 2.4, 3.0,( ),( ),
( )。
1.7
1.8
3.6
4.2
4.8
后一个数比前一个数多0.1。
后一个数比前一个数多0.6。
+0.1
+0.1
+0.1
+0.1
+0.6
+0.6
+0.6
+0.6
11.小新从家到学校要走1.2千米。他走了0.3千米后又回家取了一本书,这样他比平时上学要多走多少千米?
家
学校
1.2千米
0.3千米
观察发现:
多走部分为0.3+0.3=0.6(千米)
先画出小新的行走路线。
答:这样他比平时上学要多走0.6千米。
拓展提升
先算出半桶油的质量
再算油桶的质量
油连桶总质量-用去一半后剩余质量
剩余质量-半桶油质量
一桶油连桶共重5.2千克,用去一半后连桶共重2.7千克。这个油桶重多少千克?
一桶油+桶=5.2千克
半桶油+桶=2.7千克
一桶油连桶共重5.2千克,用去一半后连桶共重2.7千克。这个油桶重多少千克?
5.2 2.7=2.5(千克)
答:这个油桶重0.2千克。
2.7 2.5=0.2(千克)
人教版数学三年级(下)
练习二十一
7
小数的初步认识
重点回顾
列竖式计算小数加、减法的方法是什么?
1.相同数位对齐(小数点对齐)。
2.按整数加减法的方法计算。
3.得数小数点要和加数、减数或被减数对齐。
解决小数加、减法的实际问题过程中,你发现了什么?
解决小数加、减法的实际问题的步骤
1.先明确所求问题是什么。
2.根据这个问题,整理信息。
3.分析题意并列出算式,然后进行计算。
解决小数加、减法的实际问题过程中,你发现了什么?
1. 在解决有关小数的加、减法问题时,可以从不同的角度思考,选择不同的解题方法。
2.解决问题的不同方法可以互相检验。
2.3
0.8
3.9
1.
练习巩固
+ =
4.5
1.4
6.2
6.8
2.2
10.1
=
2.7
4.1
8.4
1.5
0.3
7.5
1.2
3.8
0.9
列竖式计算时,注意小数点要对齐。
(教材第98~100页练习二十一)
2.
(1)《动脑筋》比《童话故事选》便宜多少元?
6.8元
3.4元
6.8-3.4=
3.4(元)
3.4
6.8
3.4
-
答:《动脑筋》比《童话故事选》便宜3.4元。
也就是求3.4和6.8的和,用减法计算,列式为6.8-3.4。
可以先算出一共花了多少钱,再跟10元比较。
6.8+3.4=
10.2(元)
答:各买1本书,10元钱不够。
10.2>10
2.
6.8元
3.4元
(2)各买1本书,10元钱够不够?
3.计算下面各题。
2.1
+
4.8
6
9
.
1.5
+
7.5
9
0
.
1
8.7
6.3
2
4
.
10.0
3.6
6
4
.
.
3.2
1.7
1
5
.
14.6
+
5.7
0
3
.
1
.
2
1
31.8
17.2
4
6
.
1
.
20.7
+
14.9
5
6
.
3
1
.
先把小数点对齐,再按照整数加、减法的法则进行计算,得数里的小数点要和横线上的小数点对齐。
实际质量-货车自重=货物质量
货物质量大于最大载质量。
货物质量小于或等于最大载质量。
超载
不超载
4.货车自重2.8吨。它是否超载了?
满载时共重8.7吨。
载质量:6吨
方法一
8.7-2.8=5.9(吨)
5.9吨<6吨
答:它没有超载。
4.货车自重2.8吨。它是否超载了?
满载时共重8.7吨。
载质量:6吨
方法一
最大载质量+货车自重=不超载的最大质量
实际质量大于不超载的最大质量。
实际质量小于或等于不超载的最大载质量。
超载
不超载
4.货车自重2.8吨。它是否超载了?
满载时共重8.7吨。
载质量:6吨
方法二
6+2.8=8.8(吨)
8.8吨>8.7吨
答:它没有超载。
4.货车自重2.8吨。它是否超载了?
满载时共重8.7吨。
载质量:6吨
方法二
5.根据图中的涂色部分写出小数,再比较大小。
( ) ( )
>
( ) ( )
<
0.7
0.5
0.9
1.2
把一个整体平均分成10份,每份0.1,几份也就十分之几,零点几。
6.
(1)哪种玩具最贵?最贵的比最便宜的玩具贵多少钱?
最贵
最便宜
7.1-0.8=6.3(元)
答:机器人最贵,最贵的比最便宜的玩具贵6.3元。
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
观察这些价格,整数部分都不相同,直接比较整数部分即可。
6.
(2)挑选两个你最喜欢的玩具,需要多少钱?
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
答案不唯一,例如:
5.5+3.7=9.2(元)
答:需要9.2元。
6.
(3)小东有10元,买一个 后,还可以买哪两个玩具?
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
先算出剩余钱数,所买玩具总和不超过剩余钱数即可。
6.
(3)小东有10元,买一个 后,还可以买哪两个玩具?
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
答案不唯一,例如:
10-5.5=4.5(元)
买喇叭和魔方:
0.8+3.7=4.5(元)
6.
(4)你还能提出一个数学问题并解答吗?
2.8元
0.8元
6.2元
5.5元
3.7元
4.3元
4.3元
1.6元
答案不唯一,例如:
买一个玩具熊和1个皮球一共多少钱?
4.3+1.6=5.9(元)
答:一共5.9元。
7.小丽从儿童乐园上车,要到光明街站下车。如果每两站间相距为1千米,小丽要付车费多少钱
坐10站或10站以内都只要1元。
1
2
超过10站,每站增加0.2元。
到光明站下车共坐12站,用连加计算。
1+0.2+0.2=1.4(元)
答:小丽要付车费1.4元。
7.小丽从儿童乐园上车,要到光明街站下车。如果每两站间相距为1千米,小丽要付车费多少钱
(1)长颈鹿现在能上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
方法一
先算犀牛和长颈鹿的总重。
小于或等于4吨,可以过桥。
大于4吨,不能过桥。
再跟限重4吨比较。
(1)长颈鹿现在能上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
方法一
2.7+1.5=4.2(吨)
4.2吨>4吨
答:长颈鹿现在不能上桥。
(1)长颈鹿现在能上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
方法二
先算犀牛上桥后剩余最大限重。
小于或等于长颈鹿的体重,不可以过桥。
大于长颈鹿的体重,可以过桥。
再跟长颈鹿的体重比较。
(1)长颈鹿现在能上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
方法二
4-2.7=1.3(吨)
1.3吨<1.5吨
答:长颈鹿现在不能上桥。
(2)棕熊现在能上桥吗?斑马可以和它一起上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
先算犀牛上桥后剩余最大限重。
将棕熊体重跟剩余最大限重比较,大于剩余部分,不可以,小于或等于剩余部分,可以。
将棕熊和斑马的体重和跟剩余最大限重比较,大于剩余部分,不可以,小于或等于剩余部分,可以。
(2)棕熊现在能上桥吗?斑马可以和它一起上桥吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
4-2.7=1.3(吨) 0.8吨<1.3吨
0.8+0.3=1.1(吨)1.1吨<1.3吨
答:棕熊现在能上桥,斑马可以和它一起上桥。
(3)你还能提出其他数学问题并解答吗?
8.
2.7吨
1.5吨
0.3吨
0.8吨
限重4吨
长颈鹿和棕熊可以一起过桥吗?
1.5+0.8=2.3(吨) 2.3吨<4吨
答:长颈鹿和棕熊可以一起过桥。
答案不唯一
9.
3个城市城镇居民人均住房使用面积如下表。你能提出哪些问题?你会解答提出的问题吗?
城市 A B C
面积/平方米 14.6 16.7 17.6
本题可以提出相关的加法或减法解决的问题。
17.6 16.7=0.9(平方米)
例如:B市城镇居民人均住房使用面积比C市少多少平方米?
答:少0.9平方米。
9.
3个城市城镇居民人均住房使用面积如下表。你能提出哪些问题?你会解答提出的问题吗?
城市 A B C
面积/平方米 14.6 16.7 17.6
10.
按规律接着往下写。
(1)1.1, 1.2, 1.3, 1.4, 1.5,( ),( ),
( )。
1.6
(2) 0.6,1.2, 1.8, 2.4, 3.0,( ),( ),
( )。
1.7
1.8
3.6
4.2
4.8
后一个数比前一个数多0.1。
后一个数比前一个数多0.6。
+0.1
+0.1
+0.1
+0.1
+0.6
+0.6
+0.6
+0.6
11.小新从家到学校要走1.2千米。他走了0.3千米后又回家取了一本书,这样他比平时上学要多走多少千米?
家
学校
1.2千米
0.3千米
观察发现:
多走部分为0.3+0.3=0.6(千米)
先画出小新的行走路线。
答:这样他比平时上学要多走0.6千米。
拓展提升
先算出半桶油的质量
再算油桶的质量
油连桶总质量-用去一半后剩余质量
剩余质量-半桶油质量
一桶油连桶共重5.2千克,用去一半后连桶共重2.7千克。这个油桶重多少千克?
一桶油+桶=5.2千克
半桶油+桶=2.7千克
一桶油连桶共重5.2千克,用去一半后连桶共重2.7千克。这个油桶重多少千克?
5.2 2.7=2.5(千克)
答:这个油桶重0.2千克。
2.7 2.5=0.2(千克)
