2021-2022学年鲁教版(五四制)八年级数学上册第5章平行四边形 单元达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学上册第5章平行四边形 单元达标测评(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 342.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 17:07:00 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学上册《第5章平行四边形》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,在 ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为( )
A.3 B.6 C.8 D.12
2.如图,A、B两地被池塘隔开,在没有任何测量工具的情况下,小强通过下面的方法估测出A、B间的距离:先在AB外选一点C,然后步测出AC、BC的中点D、E,并且步测出DE长,由此知道AB长.若步测DE长为50m,则A,B间的距离是( )
A.25m B.50m C.75m D.100m
3.矩形ABCD中,R,P分别是边DC,BC上的点,点E、F分别是AP、RP的中点,当P在BC上由B向C移动而R不动时,EF的长( )
A.逐渐增大 B.不改变 C.逐渐减小 D.不能确定
4.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.10 B.12 C.14 D.16
5.六边形共有几条对角线( )
A.6 B.7 C.8 D.9
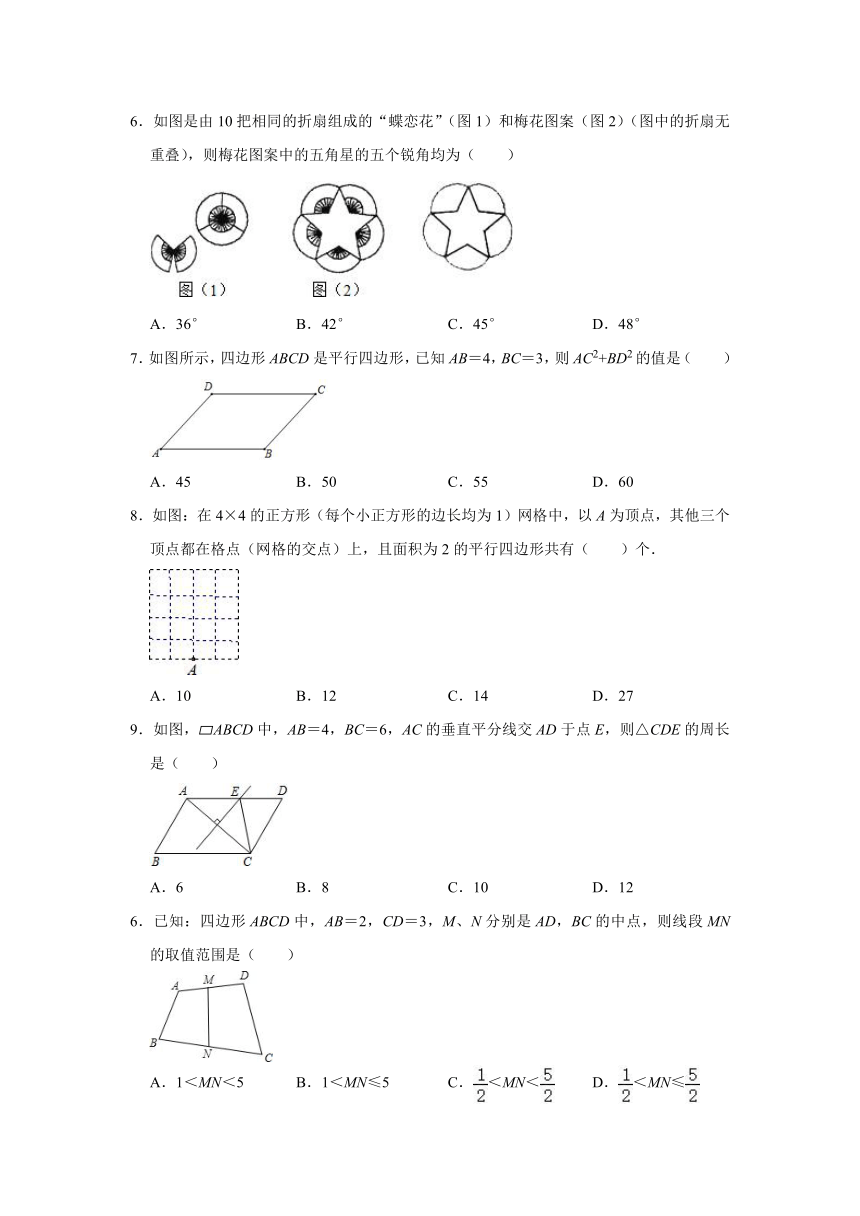
6.如图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )
A.36° B.42° C.45° D.48°
7.如图所示,四边形ABCD是平行四边形,已知AB=4,BC=3,则AC2+BD2的值是( )
A.45 B.50 C.55 D.60
8.如图:在4×4的正方形(每个小正方形的边长均为1)网格中,以A为顶点,其他三个顶点都在格点(网格的交点)上,且面积为2的平行四边形共有( )个.
A.10 B.12 C.14 D.27
9.如图, ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.6 B.8 C.10 D.12
6.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<5 B.1<MN≤5 C.<MN< D.<MN≤
二.填空题(共9小题,满分36分)
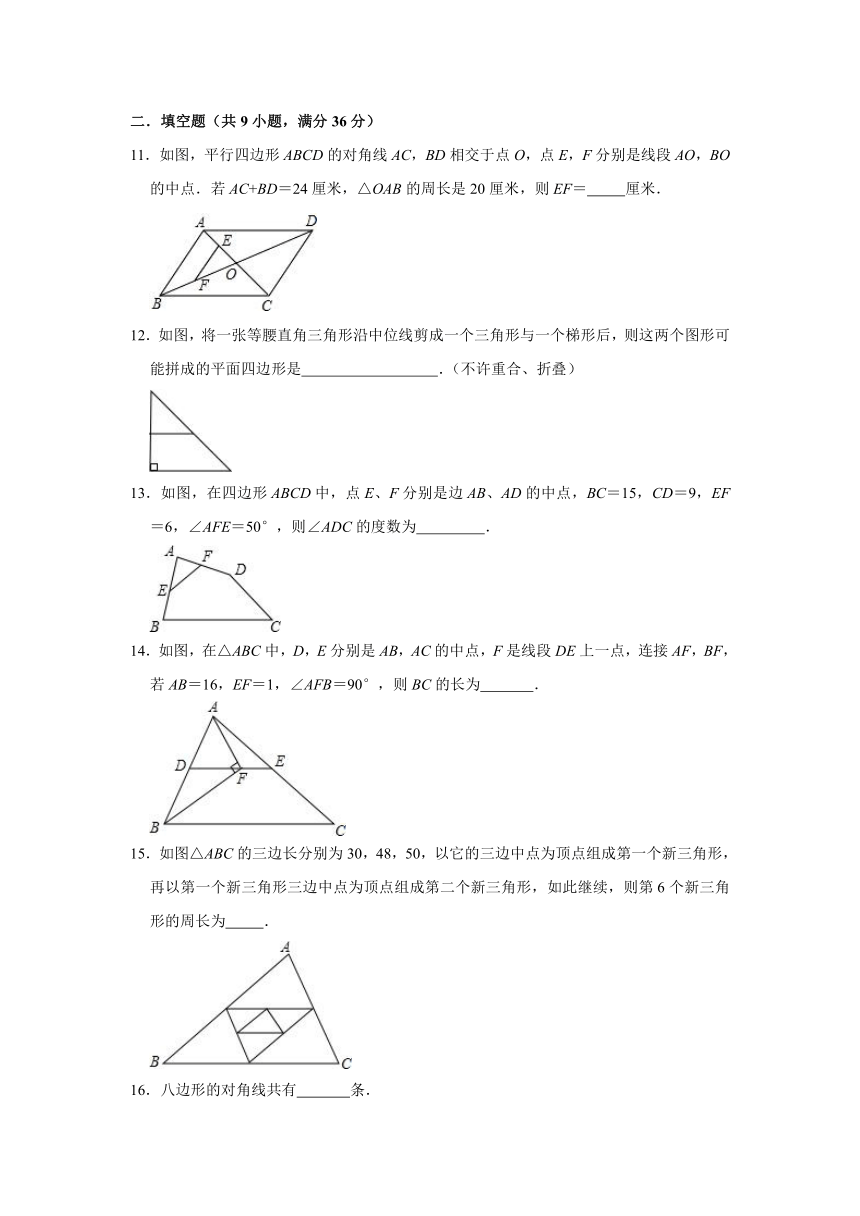
11.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是20厘米,则EF= 厘米.
12.如图,将一张等腰直角三角形沿中位线剪成一个三角形与一个梯形后,则这两个图形可能拼成的平面四边形是 .(不许重合、折叠)
13.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,则∠ADC的度数为 .
14.如图,在△ABC中,D,E分别是AB,AC的中点,F是线段DE上一点,连接AF,BF,若AB=16,EF=1,∠AFB=90°,则BC的长为 .
15.如图△ABC的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为 .
16.八边形的对角线共有 条.
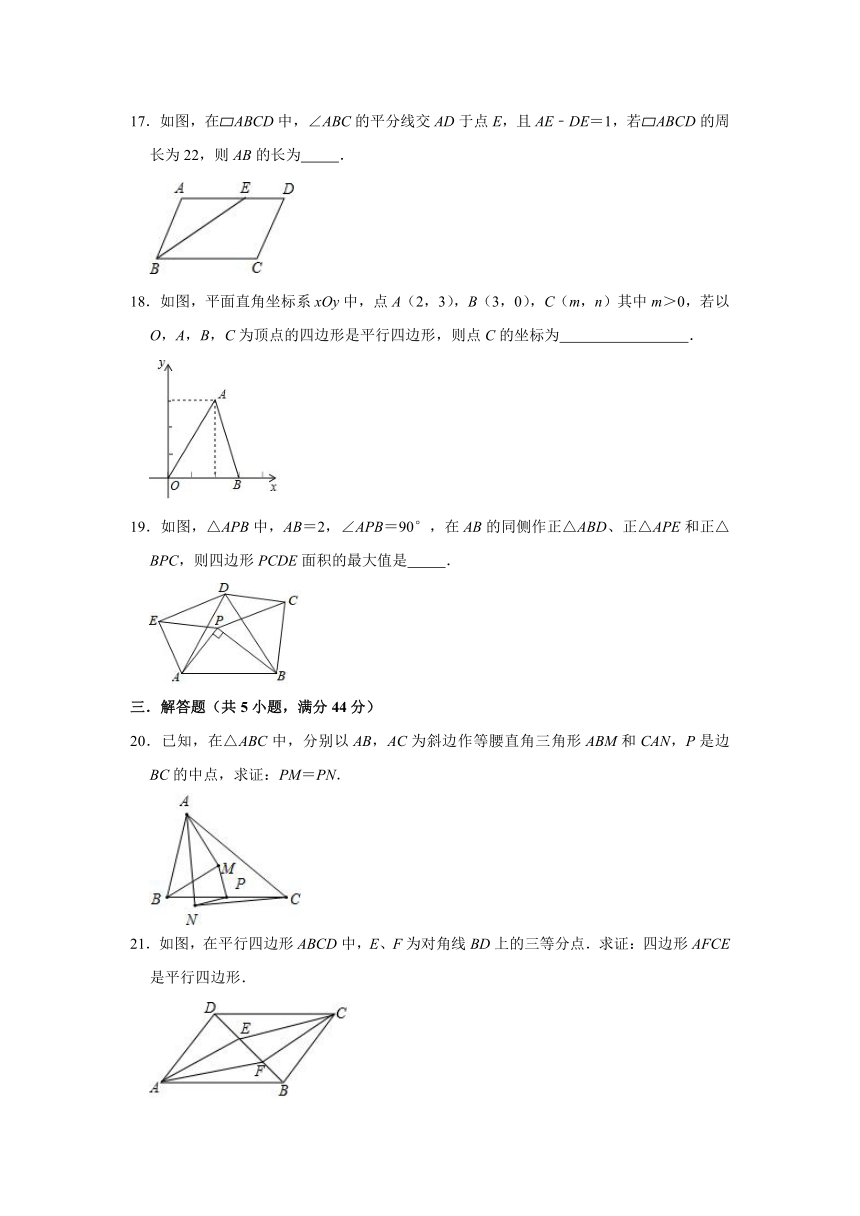
17.如图,在 ABCD中,∠ABC的平分线交AD于点E,且AE﹣DE=1,若 ABCD的周长为22,则AB的长为 .
18.如图,平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n)其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为 .
19.如图,△APB中,AB=2,∠APB=90°,在AB的同侧作正△ABD、正△APE和正△BPC,则四边形PCDE面积的最大值是 .
三.解答题(共5小题,满分44分)
20.已知,在△ABC中,分别以AB,AC为斜边作等腰直角三角形ABM和CAN,P是边BC的中点,求证:PM=PN.
21.如图,在平行四边形ABCD中,E、F为对角线BD上的三等分点.求证:四边形AFCE是平行四边形.
22.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
23.如图等边三角形ABC的边长为2,D、E分别为AB、AC的中点,延长BC至F,使CF=BC,连接CD和EF.
(1)求证:DE=CF
(2)求EF的长.
24.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵四边形ABCD是平行四边形,
∴AB=CD;
又∵E、F分别是AD、BD的中点,
∴EF是△DAB的中位线,
∴EF=AB,
∴EF=CD=3,
∴CD=6;
故选:B.
2.解:∵D、E分别是AC、BC的中点,
∴DE是△ABC的中位线,
根据三角形的中位线定理,得:AB=2DE=100m.
故选:D.
3.解:根据题意画出图形,如图所示:
∵R在CD上不动,
∴AR值不变,
∵点E、F分别是AP、RP的中点,
∴EF=AR,
∴不管P怎样移动,EF的值永远等于AR,即不改变.
故选:B.
4.解:如图,∵∠AFC=90°,E是AC的中点,
∴Rt△ACF中,EF=AC==5,
∴DE=1+5=6;
∵D,E分别是AB,AC的中点,
∴DE为△ABC的中位线,
∴BC=2DE=12,
故选:B.
5.解:根据题意得:=9,
则六边形共有9条对角线,
故选:D.
6.解:如图,梅花扇的内角的度数是:360°÷3=120°,
180°﹣120°=60°,
正五边形的每一个内角=(5﹣2) 180°÷5=108°,
∴梅花图案中的五角星的五个锐角均为:108°﹣60°=48°.
故选:D.
7.解:如图,作DE⊥AB于E,CF⊥AB交AB的延长线于F.连接AC、BD.设BF=a,CF=b.
∵四边形ABCD是平行四边形,DE⊥AB,CF⊥AB,
∴AD=BC,DE=CF=b,∠DEA=∠F=90°,
∴Rt△ADE≌△Rt△BCF,
∴AE=BF=a,
∴AC2+BD2=CF2+AF2+DE2+BE2
=b2+(4+a)2+b2+(4﹣a)2
=2(a2+b2)+32
=18+32=50,
故选:B.
8.解:以AB为一边,另两顶点在MG上的有四边形ABMI、ABQO、ABIG、共3个,
以AF为一边,另两顶点在MG上的有四边形AFGI、AFOQ、AFIM共3个,
以AC为一边,另两顶点在PH上的有四边形ACPZ、ACZN、ACNV、ACVH,共4个,
以AE为一边,另两顶点在PH上的有四边形EAPZ、EAZN、EANV、EAVH,共4个,
以AI为一边,另两顶点在YF上的有四边形AIHG、AILH、AIYL,共3个,
以AI为一边,另两顶点在XB上的有四边形AIPM、AITP、AIXT,共3个,
以AN为一边,另两顶点在ER′上的有四边形ANKO,ANR′V共2个,
以AN为一边,另两顶点在RC上的有四边形ANSQ、ANRZ,共2个,
以及正方形AONQ,
还有平行四边形AOYK和AQXS,
共3+3+4+4+3+3+2+2+1+2=27个,
故选:D.
9.解:∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∵AC的垂直平分线交AD于点E,
∴AE=CE,
∴△CDE的周长=DE+CE+DC=DE+AE+DC=AD+DC=6+4=10;
故选:C.
10.解:连接BD,过M作MG∥AB,连接NG.
∵M是边AD的中点,AB=2,MG∥AB,
∴MG是△ABD的中位线,BG=GD,MG=AB=×2=1;
∵N是BC的中点,BG=GD,CD=3,
∴NG是△BCD的中位线,NG=CD=×3=,
在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,即﹣1<MN<+1,
∴<MN<,
当MN=MG+NG,即MN=时,四边形ABCD是梯形,
故线段MN长的取值范围是<MN≤.
故选:D.
二.填空题(共9小题,满分36分)
11.解:∵ ABCD的对角线AC,BD相交于点O,
∴点O是AC、BD的中点,
∵AC+BD=24厘米,
∴OB+0A=(AC+BD)=12厘米,
∵△OAB的周长是20厘米,
∴AB=20﹣12=8厘米,
∵ ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,
∴EF=AB=4厘米,
故答案为:4.
12.解:
如图:可拼成以上三种图形:等腰梯形、矩形、平行四边形.
13.解:连接BD,
∵E、F分别是边AB、AD的中点,
∴EF∥BD,BD=2EF=12,
∴∠ADB=∠AFE=50°,
BD2+CD2=225,BC2=225,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=140°,
故答案为:140°.
14.解:∵∠AFB=90°,点D是AB的中点,
∴DF=AB=8,
∵EF=1,
∴DE=9,
∵D、E分别是AB,AC的中点,
∴BC=2DE=18,
故答案为:18
15.解:
如图,∵E、F分别为AB、AC的中点,
∴EF=BC,同理可得DF=AC,DE=AB,
∴EF+DF+DE=(AB+BC+CA),
即△DEF的周长=△ABC的周长,
∴第二个三角形的周长是原三角形周长的,
同理可得△GHI的周长=△DEF的周长=△ABC的周长=()2△ABC的周长,
∴第三个三角形的周长是原三角形周长的()2,
∴第六个三角形的周长是原三角形周长的()5=,
∵原三角形的三边长为30,48,50,
∴原三角形的周长为128,
∴第一个新三角形的周长为64,
∴第六个三角形的周长=64×=2
故答案为:2.
16.解:八边形的对角线条数应该是:=20,
故答案为:20.
17.解:设AE=x则DE=x﹣1,
∵四边形ABCD是平行四边形,
∴AD=CB,AB=DC,AD∥BC,
∴∠CBE=∠AEB,
∵BE平分∠ABC,
∴∠CBE=∠ABE,
∴∠AEB=∠ABE,
∴AB=AE=x,
∵ ABCD的周长为22,
∴2x+2(x+x﹣1)=22,
解得:x=4,
故答案为:4.
18.解:①当四边形OACB是平行四边形时,OC交AB于E.则AE=EB,OE=EC.
∵点A(2,3),B(3,0),
∴E(,),
∴C(5,3),
②当四边形OABC′是平行四边形时,OB交AC′于F,则OF=FB,FA=FC′,
∵B(3,0),
∴F(,0),
∴=,=0,
∴m=1,n=﹣3,
∴C(1,﹣3),
故答案为(5,3)或(1,﹣3).
19.解:如图所示,过P作PG⊥AB于G,过P作PH⊥AE,交AE于H,
∵∠APE=∠BPC=60°,∠APB=90°,
∴∠EPC=150°,
∵△APE是正三角形,PH⊥AE,
∴∠APH=∠EPH=30°,
∴∠CPH=180°,即点C、P、H在一条直线上,
∵正△ABD、正△APE和正△BPC,
∴AE=AP,AD=AB,BP=CP,∠EAP=∠DAB=60°=∠CPB,
∴∠DAE=∠BAP,
∴△AED≌△APB(SAS),
∴ED=BP,
∴ED=CP,
同理可得EP=DC,
∴四边形PCDE是平行四边形,
∵∠EPH=30°,
∴EH=EP=AP,
∴S平行四边形CDEP=EH×CP=AP×BP=S△ABP,
∵AB=2,∠APB=90°,
∴以AB为直径作圆,当PG最大时,S△ABP的面积最大,
此时GP为半径,
∴S△ABP=×2×1=1,
∴四边形PCDE面积的最大值是1.
故答案为:1.
三.解答题(共5小题,满分44分)
20.解:如图,分别取AB、AC的中点D、Q;
连接DM、DP;QN、QP;
∵点P为BC的中点,
∴DP∥AC,DP=AC;同理可证:
PQ∥AB,PQ=AB;
∴∠BDP=∠PQC=∠BAC(设为α);
∵△ABM、△ACN均为等腰直角三角形,
且D、Q均为AB、AC的中点,
∴MD=AB,NQ=AC,∠MDB=∠NQC=90°,
∴MD=PQ、PD=NQ,∠MDP=∠PQN=90°﹣α;
在△MDP与△PQN中,
,
∴△MDP≌△PQN(SAS),
∴PM=PN.
21.证明:
∵四边形ABCD为平行四边形,
∴∠ADB=∠DBC,DA=CB,
∵E、F为BD的三等分点,
∴DE=FB.
在△ADE和△CBF中
∴△ADE≌△CBF(SAS),
∴AE=CF,
同理△CDE≌△ABF,
∴AF=CE,
∴四边形AFCE是平行四边形.
22.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∵在△ABC和△AED中,,
∴△ABC≌△EAD.
(2)解:∵AE平分∠DAB,
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°.
∵△ABC≌△EAD,
∴∠AED=∠BAC=85°.
23.解:(1)证明:∵DE分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴,
又∵,
∴DE=CF;
(2)∵△ABC是等边三角形,D是AB的中点,
∴,CD⊥AB,
在Rt△BDC中,BD2+CD2=BC2,
即,
∴CD=3,
又∵DE是△ABC的中位线,
∴DE∥CF,
∵DE=CF,
∴四边形DCFE是平行四边形,
∴EF=CD=3.
24.解:(1)作AM⊥BC于M,设AC交PE于N.如图所示:
∵∠BAC=90°,∠B=45°,
∴∠C=45°=∠B,
∴AB=AC,
∴BM=CM,
∴AM=BC=5,
∵AD∥BC,
∴∠PAN=∠C=45°,
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5﹣t,
∵CE=CQ﹣QE=2t﹣2,
∴5﹣t=2t﹣2,
解得:t=,所以BQ=BC﹣CQ=10﹣2×=;
(2)存在,t=4或12;理由如下:
若以A,B,E,P为顶点的四边形为平行四边形,
则AP=BE,
∴t=10﹣2t+2或t=2t﹣2﹣10
解得:t=4或12
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12.
一.选择题(共10小题,满分40分)
1.如图,在 ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为( )
A.3 B.6 C.8 D.12
2.如图,A、B两地被池塘隔开,在没有任何测量工具的情况下,小强通过下面的方法估测出A、B间的距离:先在AB外选一点C,然后步测出AC、BC的中点D、E,并且步测出DE长,由此知道AB长.若步测DE长为50m,则A,B间的距离是( )
A.25m B.50m C.75m D.100m
3.矩形ABCD中,R,P分别是边DC,BC上的点,点E、F分别是AP、RP的中点,当P在BC上由B向C移动而R不动时,EF的长( )
A.逐渐增大 B.不改变 C.逐渐减小 D.不能确定
4.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.10 B.12 C.14 D.16
5.六边形共有几条对角线( )
A.6 B.7 C.8 D.9
6.如图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( )
A.36° B.42° C.45° D.48°
7.如图所示,四边形ABCD是平行四边形,已知AB=4,BC=3,则AC2+BD2的值是( )
A.45 B.50 C.55 D.60
8.如图:在4×4的正方形(每个小正方形的边长均为1)网格中,以A为顶点,其他三个顶点都在格点(网格的交点)上,且面积为2的平行四边形共有( )个.
A.10 B.12 C.14 D.27
9.如图, ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.6 B.8 C.10 D.12
6.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<5 B.1<MN≤5 C.<MN< D.<MN≤
二.填空题(共9小题,满分36分)
11.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是20厘米,则EF= 厘米.
12.如图,将一张等腰直角三角形沿中位线剪成一个三角形与一个梯形后,则这两个图形可能拼成的平面四边形是 .(不许重合、折叠)
13.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=15,CD=9,EF=6,∠AFE=50°,则∠ADC的度数为 .
14.如图,在△ABC中,D,E分别是AB,AC的中点,F是线段DE上一点,连接AF,BF,若AB=16,EF=1,∠AFB=90°,则BC的长为 .
15.如图△ABC的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为 .
16.八边形的对角线共有 条.
17.如图,在 ABCD中,∠ABC的平分线交AD于点E,且AE﹣DE=1,若 ABCD的周长为22,则AB的长为 .
18.如图,平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n)其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为 .
19.如图,△APB中,AB=2,∠APB=90°,在AB的同侧作正△ABD、正△APE和正△BPC,则四边形PCDE面积的最大值是 .
三.解答题(共5小题,满分44分)
20.已知,在△ABC中,分别以AB,AC为斜边作等腰直角三角形ABM和CAN,P是边BC的中点,求证:PM=PN.
21.如图,在平行四边形ABCD中,E、F为对角线BD上的三等分点.求证:四边形AFCE是平行四边形.
22.如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
23.如图等边三角形ABC的边长为2,D、E分别为AB、AC的中点,延长BC至F,使CF=BC,连接CD和EF.
(1)求证:DE=CF
(2)求EF的长.
24.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵四边形ABCD是平行四边形,
∴AB=CD;
又∵E、F分别是AD、BD的中点,
∴EF是△DAB的中位线,
∴EF=AB,
∴EF=CD=3,
∴CD=6;
故选:B.
2.解:∵D、E分别是AC、BC的中点,
∴DE是△ABC的中位线,
根据三角形的中位线定理,得:AB=2DE=100m.
故选:D.
3.解:根据题意画出图形,如图所示:
∵R在CD上不动,
∴AR值不变,
∵点E、F分别是AP、RP的中点,
∴EF=AR,
∴不管P怎样移动,EF的值永远等于AR,即不改变.
故选:B.
4.解:如图,∵∠AFC=90°,E是AC的中点,
∴Rt△ACF中,EF=AC==5,
∴DE=1+5=6;
∵D,E分别是AB,AC的中点,
∴DE为△ABC的中位线,
∴BC=2DE=12,
故选:B.
5.解:根据题意得:=9,
则六边形共有9条对角线,
故选:D.
6.解:如图,梅花扇的内角的度数是:360°÷3=120°,
180°﹣120°=60°,
正五边形的每一个内角=(5﹣2) 180°÷5=108°,
∴梅花图案中的五角星的五个锐角均为:108°﹣60°=48°.
故选:D.
7.解:如图,作DE⊥AB于E,CF⊥AB交AB的延长线于F.连接AC、BD.设BF=a,CF=b.
∵四边形ABCD是平行四边形,DE⊥AB,CF⊥AB,
∴AD=BC,DE=CF=b,∠DEA=∠F=90°,
∴Rt△ADE≌△Rt△BCF,
∴AE=BF=a,
∴AC2+BD2=CF2+AF2+DE2+BE2
=b2+(4+a)2+b2+(4﹣a)2
=2(a2+b2)+32
=18+32=50,
故选:B.
8.解:以AB为一边,另两顶点在MG上的有四边形ABMI、ABQO、ABIG、共3个,
以AF为一边,另两顶点在MG上的有四边形AFGI、AFOQ、AFIM共3个,
以AC为一边,另两顶点在PH上的有四边形ACPZ、ACZN、ACNV、ACVH,共4个,
以AE为一边,另两顶点在PH上的有四边形EAPZ、EAZN、EANV、EAVH,共4个,
以AI为一边,另两顶点在YF上的有四边形AIHG、AILH、AIYL,共3个,
以AI为一边,另两顶点在XB上的有四边形AIPM、AITP、AIXT,共3个,
以AN为一边,另两顶点在ER′上的有四边形ANKO,ANR′V共2个,
以AN为一边,另两顶点在RC上的有四边形ANSQ、ANRZ,共2个,
以及正方形AONQ,
还有平行四边形AOYK和AQXS,
共3+3+4+4+3+3+2+2+1+2=27个,
故选:D.
9.解:∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∵AC的垂直平分线交AD于点E,
∴AE=CE,
∴△CDE的周长=DE+CE+DC=DE+AE+DC=AD+DC=6+4=10;
故选:C.
10.解:连接BD,过M作MG∥AB,连接NG.
∵M是边AD的中点,AB=2,MG∥AB,
∴MG是△ABD的中位线,BG=GD,MG=AB=×2=1;
∵N是BC的中点,BG=GD,CD=3,
∴NG是△BCD的中位线,NG=CD=×3=,
在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,即﹣1<MN<+1,
∴<MN<,
当MN=MG+NG,即MN=时,四边形ABCD是梯形,
故线段MN长的取值范围是<MN≤.
故选:D.
二.填空题(共9小题,满分36分)
11.解:∵ ABCD的对角线AC,BD相交于点O,
∴点O是AC、BD的中点,
∵AC+BD=24厘米,
∴OB+0A=(AC+BD)=12厘米,
∵△OAB的周长是20厘米,
∴AB=20﹣12=8厘米,
∵ ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,
∴EF=AB=4厘米,
故答案为:4.
12.解:
如图:可拼成以上三种图形:等腰梯形、矩形、平行四边形.
13.解:连接BD,
∵E、F分别是边AB、AD的中点,
∴EF∥BD,BD=2EF=12,
∴∠ADB=∠AFE=50°,
BD2+CD2=225,BC2=225,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=140°,
故答案为:140°.
14.解:∵∠AFB=90°,点D是AB的中点,
∴DF=AB=8,
∵EF=1,
∴DE=9,
∵D、E分别是AB,AC的中点,
∴BC=2DE=18,
故答案为:18
15.解:
如图,∵E、F分别为AB、AC的中点,
∴EF=BC,同理可得DF=AC,DE=AB,
∴EF+DF+DE=(AB+BC+CA),
即△DEF的周长=△ABC的周长,
∴第二个三角形的周长是原三角形周长的,
同理可得△GHI的周长=△DEF的周长=△ABC的周长=()2△ABC的周长,
∴第三个三角形的周长是原三角形周长的()2,
∴第六个三角形的周长是原三角形周长的()5=,
∵原三角形的三边长为30,48,50,
∴原三角形的周长为128,
∴第一个新三角形的周长为64,
∴第六个三角形的周长=64×=2
故答案为:2.
16.解:八边形的对角线条数应该是:=20,
故答案为:20.
17.解:设AE=x则DE=x﹣1,
∵四边形ABCD是平行四边形,
∴AD=CB,AB=DC,AD∥BC,
∴∠CBE=∠AEB,
∵BE平分∠ABC,
∴∠CBE=∠ABE,
∴∠AEB=∠ABE,
∴AB=AE=x,
∵ ABCD的周长为22,
∴2x+2(x+x﹣1)=22,
解得:x=4,
故答案为:4.
18.解:①当四边形OACB是平行四边形时,OC交AB于E.则AE=EB,OE=EC.
∵点A(2,3),B(3,0),
∴E(,),
∴C(5,3),
②当四边形OABC′是平行四边形时,OB交AC′于F,则OF=FB,FA=FC′,
∵B(3,0),
∴F(,0),
∴=,=0,
∴m=1,n=﹣3,
∴C(1,﹣3),
故答案为(5,3)或(1,﹣3).
19.解:如图所示,过P作PG⊥AB于G,过P作PH⊥AE,交AE于H,
∵∠APE=∠BPC=60°,∠APB=90°,
∴∠EPC=150°,
∵△APE是正三角形,PH⊥AE,
∴∠APH=∠EPH=30°,
∴∠CPH=180°,即点C、P、H在一条直线上,
∵正△ABD、正△APE和正△BPC,
∴AE=AP,AD=AB,BP=CP,∠EAP=∠DAB=60°=∠CPB,
∴∠DAE=∠BAP,
∴△AED≌△APB(SAS),
∴ED=BP,
∴ED=CP,
同理可得EP=DC,
∴四边形PCDE是平行四边形,
∵∠EPH=30°,
∴EH=EP=AP,
∴S平行四边形CDEP=EH×CP=AP×BP=S△ABP,
∵AB=2,∠APB=90°,
∴以AB为直径作圆,当PG最大时,S△ABP的面积最大,
此时GP为半径,
∴S△ABP=×2×1=1,
∴四边形PCDE面积的最大值是1.
故答案为:1.
三.解答题(共5小题,满分44分)
20.解:如图,分别取AB、AC的中点D、Q;
连接DM、DP;QN、QP;
∵点P为BC的中点,
∴DP∥AC,DP=AC;同理可证:
PQ∥AB,PQ=AB;
∴∠BDP=∠PQC=∠BAC(设为α);
∵△ABM、△ACN均为等腰直角三角形,
且D、Q均为AB、AC的中点,
∴MD=AB,NQ=AC,∠MDB=∠NQC=90°,
∴MD=PQ、PD=NQ,∠MDP=∠PQN=90°﹣α;
在△MDP与△PQN中,
,
∴△MDP≌△PQN(SAS),
∴PM=PN.
21.证明:
∵四边形ABCD为平行四边形,
∴∠ADB=∠DBC,DA=CB,
∵E、F为BD的三等分点,
∴DE=FB.
在△ADE和△CBF中
∴△ADE≌△CBF(SAS),
∴AE=CF,
同理△CDE≌△ABF,
∴AF=CE,
∴四边形AFCE是平行四边形.
22.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∵在△ABC和△AED中,,
∴△ABC≌△EAD.
(2)解:∵AE平分∠DAB,
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°.
∵△ABC≌△EAD,
∴∠AED=∠BAC=85°.
23.解:(1)证明:∵DE分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴,
又∵,
∴DE=CF;
(2)∵△ABC是等边三角形,D是AB的中点,
∴,CD⊥AB,
在Rt△BDC中,BD2+CD2=BC2,
即,
∴CD=3,
又∵DE是△ABC的中位线,
∴DE∥CF,
∵DE=CF,
∴四边形DCFE是平行四边形,
∴EF=CD=3.
24.解:(1)作AM⊥BC于M,设AC交PE于N.如图所示:
∵∠BAC=90°,∠B=45°,
∴∠C=45°=∠B,
∴AB=AC,
∴BM=CM,
∴AM=BC=5,
∵AD∥BC,
∴∠PAN=∠C=45°,
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5﹣t,
∵CE=CQ﹣QE=2t﹣2,
∴5﹣t=2t﹣2,
解得:t=,所以BQ=BC﹣CQ=10﹣2×=;
(2)存在,t=4或12;理由如下:
若以A,B,E,P为顶点的四边形为平行四边形,
则AP=BE,
∴t=10﹣2t+2或t=2t﹣2﹣10
解得:t=4或12
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12.
