2021-2022学年华东师大版八年级数学上册第14章勾股定理 达标训练(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册第14章勾股定理 达标训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 199.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 17:08:41 | ||
图片预览




文档简介
2021-2022学年华师大版八年级数学上册《第14章勾股定理》综合达标训练(附答案)
1.已知一个直角三角形斜边为20,一条直角边长为16,那么它的面积是( )
A.160 B.48 C.60 D.96
2.△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,若a=6,b=8,则c的值为( )
A.6 B.10 C.13 D.8
3.在Rt△ABC中,∠ACB=90°,AB=3,则AB2+BC2+AC2=( )
A.9 B.18 C.20 D.24
4.若一个等腰三角形的腰长为5,底边长为6,则底边上的高为( )
A.4 B.3 C.5 D.6
5.如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )
A.16 B.32 C.160 D.256
6.如图,在△ABC中,AB⊥AC,AB=5cm,BC=13cm,BD是AC边上的中线,则△BCD的面积是( )
A.15cm2 B.30cm2 C.60cm2 D.65cm2
7.两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2+b2=c2 D.a2﹣b2=c2
8.一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则该三角形的面积为( )
A.8 B.10 C.24 D.48
9.下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.6,8,10 C.8,12,15 D.9,15,17
10.若△ABC中,BC=13,AC=5,AB=12,则下列判断正确的是( )
A.∠A=90° B.∠B=90°
C.∠C=90 D.△ABC是锐角三角形
11.△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的个数有( )
A.1个 B.2个 C.3个 D.4个
12.小明想知道学校旗杆(垂直地面)的高,他发现旗杆上的绳子垂到地面还多了1m,当他把绳子拉直后,发现绳子下端拉开5m,且下端刚好接触地面,则旗杆的高是( )
A.6m B.8m C.10m D.12m
13.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是9,则正方形D的边长 .
14.如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为 .
15.如图,在三角形ABC中,AB⊥AC于点A,AB=6,AC=8,BC=10,点P是线段BC上的一点,则线段AP的最小值为 .
16.如图,已知圆柱的底面周长18cm,高为12cm,蚂蚁从A点爬到B点的最短路程是 cm.
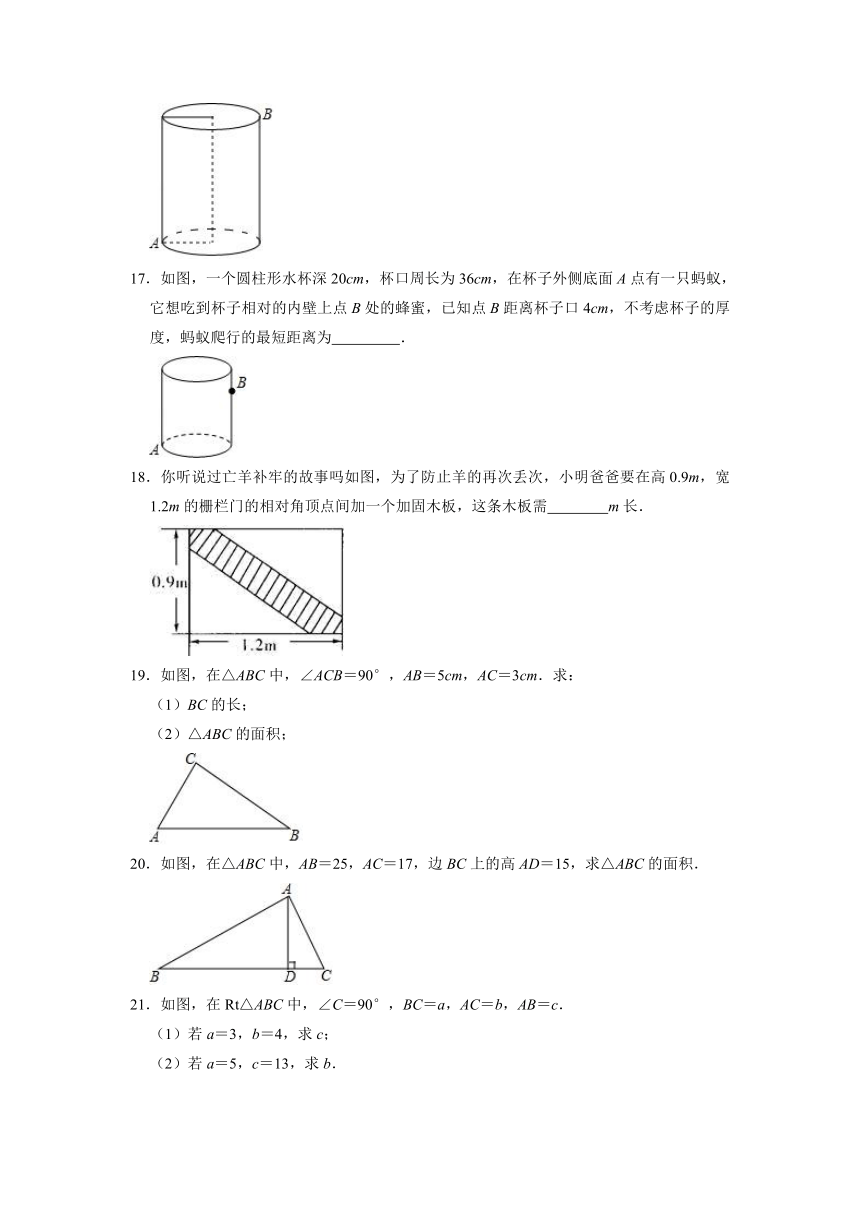
17.如图,一个圆柱形水杯深20cm,杯口周长为36cm,在杯子外侧底面A点有一只蚂蚁,它想吃到杯子相对的内壁上点B处的蜂蜜,已知点B距离杯子口4cm,不考虑杯子的厚度,蚂蚁爬行的最短距离为 .
18.你听说过亡羊补牢的故事吗如图,为了防止羊的再次丢次,小明爸爸要在高0.9m,宽1.2m的栅栏门的相对角顶点间加一个加固木板,这条木板需 m长.
19.如图,在△ABC中,∠ACB=90°,AB=5cm,AC=3cm.求:
(1)BC的长;
(2)△ABC的面积;
20.如图,在△ABC中,AB=25,AC=17,边BC上的高AD=15,求△ABC的面积.
21.如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=3,b=4,求c;
(2)若a=5,c=13,求b.
22.如图,如果每一个小正方形的边长为1在Rt△ABC中,∠C=90°.
(1)正方形P的面积= ;
(2)正方形Q的面积= ;
(3)正方形R的面积= ;
(4)你发现P、Q、R之间存在数量关系:P+Q R,即AC2+BC2 AB2.
23.如图,一块铁皮(图中阴影部分),测得AB=3,BC=4,CD=12,AD=13,∠B=90°.求阴影部分的面积.
24.如图,一架长5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=3米.
(1)求BC的长;
(2)梯子滑动后停在DE的位置,当AE为多少时,AE与BD相等?
25.2020年第一季度,我国南方多省市遭遇特大干旱,为了抗旱保收,某市准备开采地下水,经探测C处地下有水,为此C处需要爆破,已知C处与公路上的停靠站A的距离是300m,与公路上另一停靠站B的距离为400m,且CA垂直CB,为了安全,爆破点C周围250m的范围内禁止进入.问:在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?
26.平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲移到一边,花朵齐出水面,已知红莲移动的水平距离为2米,求这里的水深是多少米?
27.圆柱的高为16cm,底面半径为2cm,点B离地面8cm,一只蜘蛛以5cm/s的速度从底面上的点A处绕曲面到达点B捕食被网到的昆虫,蜘蛛到昆虫所在点B所用最短时间是多少?(π取3)
参考答案
1.解:由勾股定理得,直角三角形的另一条直角边长==12,
则直角三角形的面积=×16×12=96,
故选:D.
2.解:∵△ABC中,∠C=90°,a=6,b=8,
∴c===10.
故选:B.
3.解:∵在Rt△ABC中,∠ACB=90°,AB=3,
∴AB2+BC2+AC2=2AB2=18,
故选:B.
4.解:如图,在△ABC中,AB=AC=5,AD⊥BC,
则AD为BC边上的中线,即D为BC中点,
∴BD=DC=3,
在直角△ABD中AD==4.
故选:A.
5.解:在Rt△ACB中,AC2+BC2=AB2=256,
则正方形ADEC和正方形BCFG的面积和=AC2+BC2=256,
故选:D.
6.解:由勾股定理得,AC==12,
∵BD是AC边上的中线,
∴CD=AD=6,
∴△BCD的面积=×5×6=15(cm2),
故选:A.
7.解:根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
∴(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2.
故选:C.
8.解:设另一直角边长为x,则斜边长为(x+2),
由勾股定理得,x2+62=(x+2)2,
解得,x=8,
∴该三角形的面积=×6×8=24,
故选:C.
9.解:A、42+52≠62,不能构成直角三角形,故不符合题意;
B、62+82=102,能构成直角三角形,故符合题意;
C、82+122≠152,不能构成直角三角形,故不符合题意;
D、92+152≠172,不能构成直角三角形,故不符合题意.
故选:B.
10.解:∵52+122=169,132=169,
∴52+122=132,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,∠A=90°.
故选:A.
11.解:①由∠A=∠B﹣∠C,可知:∠B=90°,是直角三角形.
②由a2=(b+c)(b﹣c),可得a2+c2=b2,是直角三角形.
③由∠A:∠B:∠C=3:4:5,可知不是直角三角形.
④由a:b:c=5:12:13,根据勾股定理的逆定理可知是直角三角形.
故选:C.
12.解:设旗杆的高AB为xm,则绳子AC的长为(x+1)m
在Rt△ABC中,AB2+BC2=AC2
∴x2+52=(x+1)2
解得x=12
∴AB=12
∴旗杆的高12m.
故选:D.
13.解:根据勾股定理的几何意义得:SD=SA+SB+SC=9,
可知,D的边长为=3.
故答案为:3.
14.解:由勾股定理得,BC==,
∴正方形ABCD的面积=BC2=3,
故答案为:3.
15.解:∵AB⊥AC,
∴∠BAC=90°,
当AP⊥BC时,AP的值最短,
∴AP===,
∴线段AP的最小值为,
故答案为:.
16.解:沿过A点和过B点的母线剪开,展成平面,连接AB则AB的长是蚂蚁在圆柱表面从A点爬到B点的最短路程,
∵AC=9cm,BC=12cm,
∴AB==15cm,
故答案为:15.
17.解:如图:
将杯子侧面展开,作B关于EF的对称点B′,
连接B′A,则B′A即为最短距离,B'A=cm.
故答案为:30cm.
18.解:由图可知这条木板的长为==1.5m.
19.解:(1)∵∠ACB=90°,AB=5cm,AC=3cm,
∴BC==4cm;
(2)S△ABC=AC BC=6cm2.
20.解:∵在Rt△ADC中,AC=17,AD=15,
∴DC==8,
在Rt△ABD中,
∵AB=25,AD=15,
∴BD==20,
∴BC=28,
∴△ABC的面积为:×28×15=210.
21.解:
(1)∵在Rt△ABC中,∠C=90°,a=3,b=4,
∴c==5;
(2)∵在Rt△ABC中,∠C=90°,a=5,c=13,
∴b==12.
22.解:(1)正方形P的面积=1×1=1;
(2)正方形Q的面积=1×1=1;
(3)正方形R的面积=×=2;
(4)由(1)、(2)、(3)中的结论可得到P+Q=R;AC2+BC2=AB2.
故答案为:1;1;1;=;=.
23.解:如图,连接AC.
∵△ABC中,∠B=90°,AB=3,BC=4,
∴AC==5.
∵CD=12,AD=13,AC=5,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S阴影=S△ACD﹣S△ABC=×5×12﹣×3×4=30﹣6=24.
24.解:(1)∵一架长5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=3米,
∴BC==4(m),
答:BC的长为4m;
(2)当BD=AE,
则设AE=x,
故(4﹣x)2+(3+x)2=25
解得:x1=1,x2=0(舍去),
故AE=1m.
25.解:如图,过C作CD⊥AB于D,
∵AC=300米,BC=400米,∠ACB=90°,
∴根据勾股定理得AB=500米,
∵AB CD=BC AC,
∴CD=240米.
∵240米<250米,故有危险,
因此AB段公路需要暂时封锁.
26.解:设水深为h米,则红莲的高(h+1)米,且水平距离为2米,
则(h+1)2=22+h2,
解得h=1.5(米).
答:这里的水深是1.5米.
27.解:如图所示,
∵圆柱的底面半径为2cm,
∴AC=×2π×2=2π≈6(cm),
∵BC=8cm,
∴AB===10(cm),
10cm÷5cm/s=2s
答:蜘蛛到昆虫所在点B所用最短时间是2s.
1.已知一个直角三角形斜边为20,一条直角边长为16,那么它的面积是( )
A.160 B.48 C.60 D.96
2.△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,若a=6,b=8,则c的值为( )
A.6 B.10 C.13 D.8
3.在Rt△ABC中,∠ACB=90°,AB=3,则AB2+BC2+AC2=( )
A.9 B.18 C.20 D.24
4.若一个等腰三角形的腰长为5,底边长为6,则底边上的高为( )
A.4 B.3 C.5 D.6
5.如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )
A.16 B.32 C.160 D.256
6.如图,在△ABC中,AB⊥AC,AB=5cm,BC=13cm,BD是AC边上的中线,则△BCD的面积是( )
A.15cm2 B.30cm2 C.60cm2 D.65cm2
7.两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2+b2=c2 D.a2﹣b2=c2
8.一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则该三角形的面积为( )
A.8 B.10 C.24 D.48
9.下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.6,8,10 C.8,12,15 D.9,15,17
10.若△ABC中,BC=13,AC=5,AB=12,则下列判断正确的是( )
A.∠A=90° B.∠B=90°
C.∠C=90 D.△ABC是锐角三角形
11.△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的个数有( )
A.1个 B.2个 C.3个 D.4个
12.小明想知道学校旗杆(垂直地面)的高,他发现旗杆上的绳子垂到地面还多了1m,当他把绳子拉直后,发现绳子下端拉开5m,且下端刚好接触地面,则旗杆的高是( )
A.6m B.8m C.10m D.12m
13.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是9,则正方形D的边长 .
14.如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为 .
15.如图,在三角形ABC中,AB⊥AC于点A,AB=6,AC=8,BC=10,点P是线段BC上的一点,则线段AP的最小值为 .
16.如图,已知圆柱的底面周长18cm,高为12cm,蚂蚁从A点爬到B点的最短路程是 cm.
17.如图,一个圆柱形水杯深20cm,杯口周长为36cm,在杯子外侧底面A点有一只蚂蚁,它想吃到杯子相对的内壁上点B处的蜂蜜,已知点B距离杯子口4cm,不考虑杯子的厚度,蚂蚁爬行的最短距离为 .
18.你听说过亡羊补牢的故事吗如图,为了防止羊的再次丢次,小明爸爸要在高0.9m,宽1.2m的栅栏门的相对角顶点间加一个加固木板,这条木板需 m长.
19.如图,在△ABC中,∠ACB=90°,AB=5cm,AC=3cm.求:
(1)BC的长;
(2)△ABC的面积;
20.如图,在△ABC中,AB=25,AC=17,边BC上的高AD=15,求△ABC的面积.
21.如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=3,b=4,求c;
(2)若a=5,c=13,求b.
22.如图,如果每一个小正方形的边长为1在Rt△ABC中,∠C=90°.
(1)正方形P的面积= ;
(2)正方形Q的面积= ;
(3)正方形R的面积= ;
(4)你发现P、Q、R之间存在数量关系:P+Q R,即AC2+BC2 AB2.
23.如图,一块铁皮(图中阴影部分),测得AB=3,BC=4,CD=12,AD=13,∠B=90°.求阴影部分的面积.
24.如图,一架长5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=3米.
(1)求BC的长;
(2)梯子滑动后停在DE的位置,当AE为多少时,AE与BD相等?
25.2020年第一季度,我国南方多省市遭遇特大干旱,为了抗旱保收,某市准备开采地下水,经探测C处地下有水,为此C处需要爆破,已知C处与公路上的停靠站A的距离是300m,与公路上另一停靠站B的距离为400m,且CA垂直CB,为了安全,爆破点C周围250m的范围内禁止进入.问:在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?
26.平静的湖面上,有一支红莲,高出水面1米,一阵风吹来,红莲移到一边,花朵齐出水面,已知红莲移动的水平距离为2米,求这里的水深是多少米?
27.圆柱的高为16cm,底面半径为2cm,点B离地面8cm,一只蜘蛛以5cm/s的速度从底面上的点A处绕曲面到达点B捕食被网到的昆虫,蜘蛛到昆虫所在点B所用最短时间是多少?(π取3)
参考答案
1.解:由勾股定理得,直角三角形的另一条直角边长==12,
则直角三角形的面积=×16×12=96,
故选:D.
2.解:∵△ABC中,∠C=90°,a=6,b=8,
∴c===10.
故选:B.
3.解:∵在Rt△ABC中,∠ACB=90°,AB=3,
∴AB2+BC2+AC2=2AB2=18,
故选:B.
4.解:如图,在△ABC中,AB=AC=5,AD⊥BC,
则AD为BC边上的中线,即D为BC中点,
∴BD=DC=3,
在直角△ABD中AD==4.
故选:A.
5.解:在Rt△ACB中,AC2+BC2=AB2=256,
则正方形ADEC和正方形BCFG的面积和=AC2+BC2=256,
故选:D.
6.解:由勾股定理得,AC==12,
∵BD是AC边上的中线,
∴CD=AD=6,
∴△BCD的面积=×5×6=15(cm2),
故选:A.
7.解:根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
∴(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2.
故选:C.
8.解:设另一直角边长为x,则斜边长为(x+2),
由勾股定理得,x2+62=(x+2)2,
解得,x=8,
∴该三角形的面积=×6×8=24,
故选:C.
9.解:A、42+52≠62,不能构成直角三角形,故不符合题意;
B、62+82=102,能构成直角三角形,故符合题意;
C、82+122≠152,不能构成直角三角形,故不符合题意;
D、92+152≠172,不能构成直角三角形,故不符合题意.
故选:B.
10.解:∵52+122=169,132=169,
∴52+122=132,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,∠A=90°.
故选:A.
11.解:①由∠A=∠B﹣∠C,可知:∠B=90°,是直角三角形.
②由a2=(b+c)(b﹣c),可得a2+c2=b2,是直角三角形.
③由∠A:∠B:∠C=3:4:5,可知不是直角三角形.
④由a:b:c=5:12:13,根据勾股定理的逆定理可知是直角三角形.
故选:C.
12.解:设旗杆的高AB为xm,则绳子AC的长为(x+1)m
在Rt△ABC中,AB2+BC2=AC2
∴x2+52=(x+1)2
解得x=12
∴AB=12
∴旗杆的高12m.
故选:D.
13.解:根据勾股定理的几何意义得:SD=SA+SB+SC=9,
可知,D的边长为=3.
故答案为:3.
14.解:由勾股定理得,BC==,
∴正方形ABCD的面积=BC2=3,
故答案为:3.
15.解:∵AB⊥AC,
∴∠BAC=90°,
当AP⊥BC时,AP的值最短,
∴AP===,
∴线段AP的最小值为,
故答案为:.
16.解:沿过A点和过B点的母线剪开,展成平面,连接AB则AB的长是蚂蚁在圆柱表面从A点爬到B点的最短路程,
∵AC=9cm,BC=12cm,
∴AB==15cm,
故答案为:15.
17.解:如图:
将杯子侧面展开,作B关于EF的对称点B′,
连接B′A,则B′A即为最短距离,B'A=cm.
故答案为:30cm.
18.解:由图可知这条木板的长为==1.5m.
19.解:(1)∵∠ACB=90°,AB=5cm,AC=3cm,
∴BC==4cm;
(2)S△ABC=AC BC=6cm2.
20.解:∵在Rt△ADC中,AC=17,AD=15,
∴DC==8,
在Rt△ABD中,
∵AB=25,AD=15,
∴BD==20,
∴BC=28,
∴△ABC的面积为:×28×15=210.
21.解:
(1)∵在Rt△ABC中,∠C=90°,a=3,b=4,
∴c==5;
(2)∵在Rt△ABC中,∠C=90°,a=5,c=13,
∴b==12.
22.解:(1)正方形P的面积=1×1=1;
(2)正方形Q的面积=1×1=1;
(3)正方形R的面积=×=2;
(4)由(1)、(2)、(3)中的结论可得到P+Q=R;AC2+BC2=AB2.
故答案为:1;1;1;=;=.
23.解:如图,连接AC.
∵△ABC中,∠B=90°,AB=3,BC=4,
∴AC==5.
∵CD=12,AD=13,AC=5,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S阴影=S△ACD﹣S△ABC=×5×12﹣×3×4=30﹣6=24.
24.解:(1)∵一架长5米的梯子AB,顶端B靠在墙上,梯子底端A到墙的距离AC=3米,
∴BC==4(m),
答:BC的长为4m;
(2)当BD=AE,
则设AE=x,
故(4﹣x)2+(3+x)2=25
解得:x1=1,x2=0(舍去),
故AE=1m.
25.解:如图,过C作CD⊥AB于D,
∵AC=300米,BC=400米,∠ACB=90°,
∴根据勾股定理得AB=500米,
∵AB CD=BC AC,
∴CD=240米.
∵240米<250米,故有危险,
因此AB段公路需要暂时封锁.
26.解:设水深为h米,则红莲的高(h+1)米,且水平距离为2米,
则(h+1)2=22+h2,
解得h=1.5(米).
答:这里的水深是1.5米.
27.解:如图所示,
∵圆柱的底面半径为2cm,
∴AC=×2π×2=2π≈6(cm),
∵BC=8cm,
∴AB===10(cm),
10cm÷5cm/s=2s
答:蜘蛛到昆虫所在点B所用最短时间是2s.
