2021-2022学年人教版九年级数学下册第27章相似单元综合练习题(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第27章相似单元综合练习题(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 459.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 15:40:27 | ||
图片预览



文档简介
2021-2022学年人教版九年级数学下册《第27章相似》单元综合练习题(附答案)
1.若=,则=( )
A. B. C. D.
2.如果用线段a、b、c,求作线段x,使a:b=c:x,那么下列作图正确的是( )
A. B.
C. D.
3.下列说法正确的个数有( )个
①凡正方形都相似;②凡等腰三角形都相似;
③凡等腰直角三角形都相似;
④两个相似多边形的面积比为4:9,则周长的比为16:81.
A.1 B.2 C.3 D.4
4.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么下列结论正确的是( )
A.DF= B.EF= C.CD= D.BF=
5.如果两个相似三角形的面积比是4:9,则它们对应边上的中线之比为( )
A.4:9 B.9:4 C.3:2 D.2:3
6.如图,在 ABCD中,E为CD边上的中点,AE交BD于点O,若S△DOE=2,则 ABCD的面积为( )
A.8 B.12 C.16 D.24
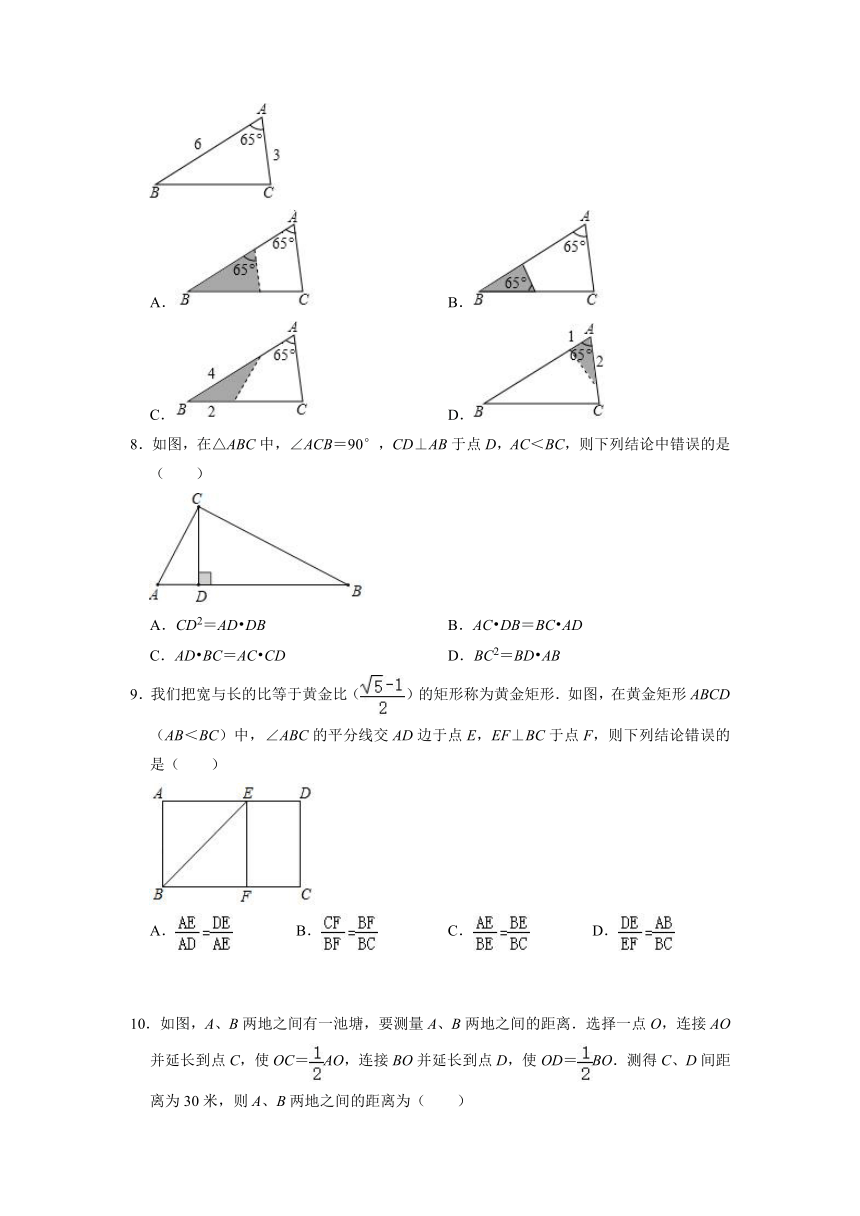
7.如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A. B.
C. D.
8.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC<BC,则下列结论中错误的是( )
A.CD2=AD DB B.AC DB=BC AD
C.AD BC=AC CD D.BC2=BD AB
9.我们把宽与长的比等于黄金比()的矩形称为黄金矩形.如图,在黄金矩形ABCD(AB<BC)中,∠ABC的平分线交AD边于点E,EF⊥BC于点F,则下列结论错误的是( )
A. B. C. D.
10.如图,A、B两地之间有一池塘,要测量A、B两地之间的距离.选择一点O,连接AO并延长到点C,使OC=AO,连接BO并延长到点D,使OD=BO.测得C、D间距离为30米,则A、B两地之间的距离为( )
A.30米 B.45米 C.60米 D.90米
11.如图,△ABC外任取一点O,连接AO、BO、CO,并取它们的中点D、E、F,得△DEF.下列说法正确的个数是( )
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;
③△ABC与△DEF周长之比为2:1;④△ABC与△DEF的面积之比为9:1.
A.1个 B.2个 C.3个 D.4个
12.如图,在△ABC中,高BD,CE相交于点F,图中与△BEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
13.如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=BC,连接GM.有如下结论:①DE=AF;②AN=AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.②③④
14.在坐标系中,已知A(6,0),B(0,8),C(0,﹣2),过点C作直线L交x轴于点D,使得以点D、C、O为顶点的三角形与△AOB相似,这样的直线一共可以作( )条.
A.3 B.4 C.5 D.6
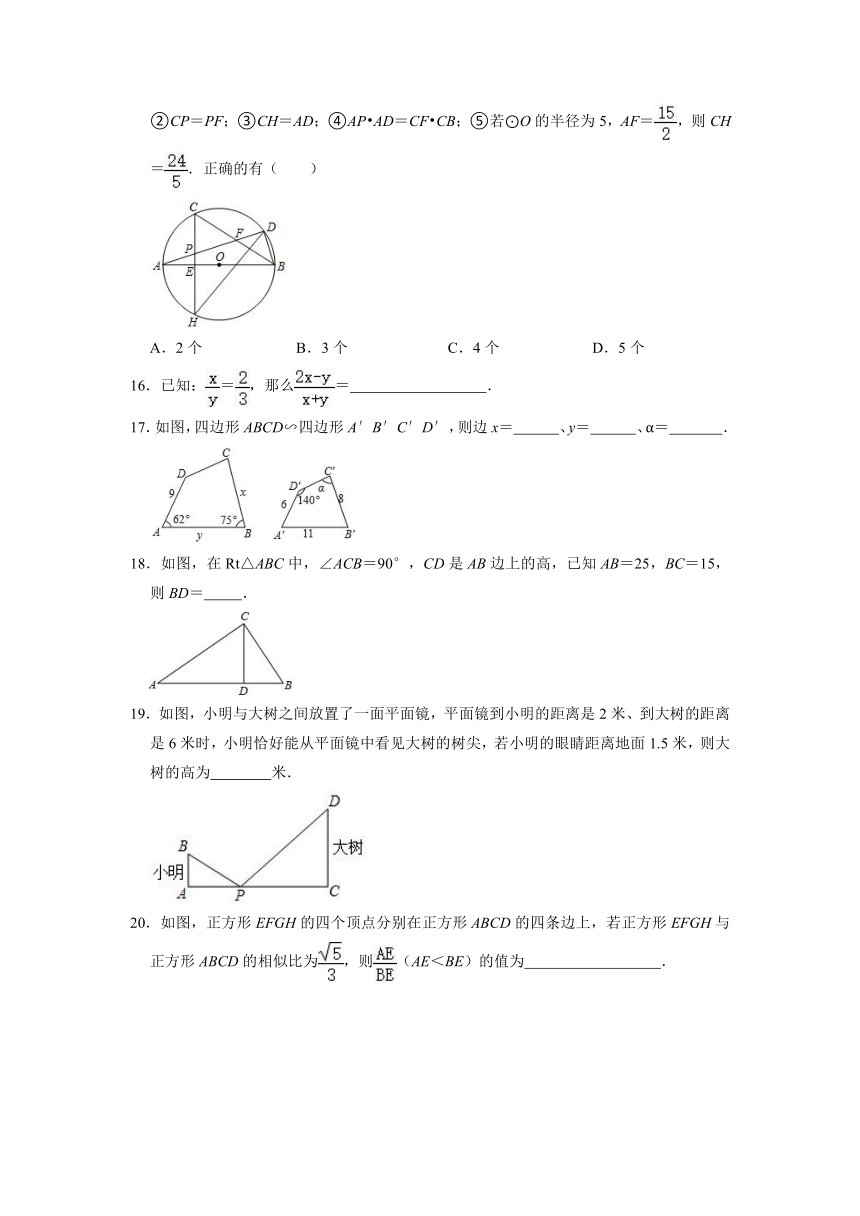
15.如图,△ABD内接于⊙O,AB为⊙O的直径,C为弧AD的中点,CH⊥AB于点E,交AD于点P,交⊙O于点H,连接DH,连接BC交AD于点F.下列结论中:①DH⊥CB;②CP=PF;③CH=AD;④AP AD=CF CB;⑤若⊙O的半径为5,AF=,则CH=.正确的有( )
A.2个 B.3个 C.4个 D.5个
16.已知:=,那么= .
17.如图,四边形ABCD∽四边形A′B′C′D′,则边x= 、y= 、α= .
18.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,已知AB=25,BC=15,则BD= .
19.如图,小明与大树之间放置了一面平面镜,平面镜到小明的距离是2米、到大树的距离是6米时,小明恰好能从平面镜中看见大树的树尖,若小明的眼睛距离地面1.5米,则大树的高为 米.
20.如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为,则(AE<BE)的值为 .
21.如图,已知,在△ABC中,∠C=90°,点D是AC上一点,∠DBC=∠A,=,那么的值为 .
22.如图,A是反比例函数y=(x>0)图象上的一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则k的值为 .
23.将边长分别为2cm,3cm,4cm的三个正方形按如图所示的方式排列,则图中阴影部分的面积为 cm2.
24.如图,已知正方形ABCD的各个顶点A、B、C、D都在⊙O上,如果P是的中点,PD与AB交于E点,那么= .
25.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CD AC;④若AB=2,则BC=﹣1,其中正确的结论的个数是 个.
26.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.
27.如图,在△ABC中,AD平分∠BAC,E是AD上一点,且BE=BD.
(1)求证:△ABE∽△ACD;
(2)若BD=1,CD=2,求的值.
28.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
29.如图,AB是⊙O的直径,弦CD⊥AB于点H,点F是上一点,连接AF交CD的延长线于点E.
(1)求证:△AFC∽△ACE;
(2)若AC=5,DC=6,当点F为的中点时,求AF的值.
参考答案
1.解:=1+
∵=
∴=
把=代入=1+=
故选:C.
2.解:A、a:b=x:c与已知a:b=c:x不符合,故选项A不正确;
B、a:b=c:x与已知a:b=c:x符合,故选项B正确;
C、a:c=x:b与已知a:b=c:x不符合,故选项C不正确;
D、a:x=b:c与已知a:b=c:x不符合,故选项D不正确;
故选:B.
3.解:①凡正方形都相似,正确;
②等腰三角形两腰相等,对应成比例,但顶角不一定相等,所以不一定相似,故本小题错误;
③凡等腰直角三角形都相似,正确;
④两个相似多边形的面积比为4:9,则周长的比为2:3,故本小题错误;
所以,说法正确的有①③共2个.
故选:B.
4.解:∵AB∥CD∥EF,AC=2,AE=5,BD=1.5,
∴,
即,
解得:DF=,
∴BF=BD+DF=,
故选:D.
5.解:∵两个相似三角形的面积比是4:9,
∴两个相似三角形的相似比是2:3,
∴对应边上的中线的比为2:3,
故选:D.
6.解:∵四边形ABCD是平行四边形,E为CD边上的中点,
∴AB∥BC,DE=DC=AB,
∴△DOE∽△BOA,
∴===,=()2,即=,
∴S△BOA=8,S△AOD=4,
∴S△BAD=12,
∴ ABCD的面积=24,
故选:D.
7.解:A、根据平行线截得的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
C、两三角形的对应角不一定相等,故两三角形不相似,故本选项符合题意;
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项不符合题意.
故选:C.
8.解:∵∠ACB=90°,CD⊥AB
∴CD2=AD DB,BC2=BD AB,
故A、D选项正确;
∵△ACD∽△CBD,
∴==,
∴AC DB=BC CD,故B选项错误;
AD BC=AC CD,故C选项正确;
故选:B.
9.解:∵矩形ABCD(AB<BC)为黄金矩形,
∴设AB=﹣1,AD=2,
∵BF平分∠ABC,而∠ABC=90°,
∴四边形ABFE为正方形,
∴AE=AB,
∵DE=2﹣(﹣1)=3﹣
∴==,
而=,
∴=,所以A选项的结论正确;
∵==,=,
∴=,所以B选项的结论正确;
∵=,=,
∴≠,所以C选项的结论错误;
∵=,=,
∴=,所以D选项正确.
故选:C.
10.解:∵△ABO和△COD中,==,
且∠AOB=∠COD,
∴△AOB∽△COD,
∴=2,
又∵CD=30m,
∴AB=60m.
故选:C.
11.解:根据位似的定义可得:△ABC与△DEF是位似图形,也是相似图形,位似比是2:1,则周长的比是2:1,因而面积的比是4:1,故①②③正确,④错误.
故选:C.
12.解:∵BD⊥AC、CE⊥AB,
∴∠BDA=∠BDC=∠CEA=∠CEB=90°,
∵∠FBE=∠ABD,
∴△FBE∽△ABD,
∵∠BFE=∠CFD,
∴△BFE∽△CFD,
∵∠FCD=∠ACE,
∴△CFD∽△CAE,
∴△BFE∽△CAE,
综上,图中与△BEF相似的三角形有△BAD、△CFD、△CAE这3个,
故选:C.
13.解:∵四边形ABCD是正方形,
∴AD=AB=CD=BC,∠CDE=∠DAF=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=∠ADF+∠CDF=90°,
∴∠ADF=∠DCE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(ASA),
∴DE=AF;故①正确;
∵AB∥CD,
∴=,
∵AF:FB=1:2,
∴AF:AB=AF:CD=1:3,
∴=,
∴=,
∵AC=AB,
∴=,
∴AN=AB;故②正确;
作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC=a,
∵∠DCE=∠DCM,∠CDE=∠CMD=90°,
∴△CMD∽△CDE,
∵∠DCE+∠DEC=∠DCE+∠HCG=90°,
∴∠DEC=∠HCG,
又∵∠CDE=∠CHG=90°,
∴△GHC∽△CDE,由△CMD∽△CDE,可得CM=a,
由△GHC∽△CDE,可得CH=a,
∴CH=MH=CM,
∵GH⊥CM,
∴GM=GC,
∴∠GMH=∠GCH,
∵∠FMG+∠GMH=90°,∠DCE+∠GCM=90°,
∴∠FMG=∠DCE,
∵∠ADF=∠DCE,
∴∠ADF=∠GMF;故③正确,
(补充方法:延长MF交CG的延长线于T,证明CG=GT,利用直角三角形斜边中线的性质即可解决问题)
设△ANF的面积为m,
∵AF∥CD,
∴==,△AFN∽△CDN,
∴△ADN的面积为3m,△DCN的面积为9m,
∴△ADC的面积=△ABC的面积=12m,
∴S△ANF:S四边形CNFB=1:11,故④错误,
故选:C.
14.解:若△AOB∽△COD,则==,
∴OD=,则D(,0)或(﹣,0).
若△AOB∽△DOC,则==,
∴OD=,则D(,0)或(﹣,0).
所以可以作出四条直线.
故选:B.
15.解:∵C为弧AD的中点,
∴=,
∴∠H=∠ABC,
∵CH⊥AB,
∴∠C+∠ABC=90°,
∴∠H+∠C=90°,
∴DH⊥BC,故①正确;
∵=,
∴∠CBD=∠ABC,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠BFD+∠DBF=90°,
∴∠C=∠BFD,
∵∠CFP=∠DFB,
∴∠C=∠CFP,
∴CP=PF,故②正确;
∵AB为⊙O的直径,C为弧AD的中点,CH⊥AB,
∴==,
∴=,
∴CH=AD;故③正确;
连接AC,BH,
则∠ACH=∠CAD,
∴AP=CP,
∵CH⊥AB,
∴=,
∴BC=BH,
∴∠BCH=∠BHC,
∴∠CFP=∠BHC,
∵∠PCF=∠BCH,
∴△CPF∽△CBH,
∴,
∴PC CH=CF CB,
∵PC=AP,CH=AD,
∴AP AD=CF CB,故④正确;
∵∠CAF=∠ABC,
又∵∠ACF=∠BCA,
∴△CAF∽△CBA,
∴===.
又∵AB=10,
∴AC=6,BC=8.
根据直角三角形的面积公式,得:AC BC=AB CE,
∴6×8=10CE.
∴CE=.
又∵CH=HE,
∴CH=2CE=.故⑤错误,
故选:C.
16.解:∵=,
∴设x=2a,y=3a,
∴==.
故答案为:.
17.解:∵四边形ABCD∽四边形A′B′C′D′,
∴==,∠C=α,∠D=∠D′=140°.
∴x=12,y=,α=∠C=360°﹣∠A﹣∠B﹣∠D=360°﹣62°﹣75°﹣140°=83°.
故答案为:12、、83°.
18.解:由射影定理得,BC2=BD AB,
∴BD==9,
故答案为:9.
19.解:根据题意可得:AB=1.5,AP=2,CP=6,∠BPA=∠DPC,∠A=∠C=90°,
∴△ABP∽△CDP,
∴=,
即:=,
∴CD=4.5(米),
故答案为:4.5.
20.解:∵正方形EFGH与正方形ABCD的相似比为,
∴不妨假设EF=k,AB=3k,
∵∠A=∠B=∠FEH=90°,
∴∠AEH+∠BEF=90°,∠BEF+∠EFB=90°,
∴∠AEH=∠EFB,
∵EH=EF,
∴△HAE≌△EBF(AAS),
∴AE=BF,设AE=BF=x则EB=3k﹣x,
在Rt△EFB中,∵EF2=BE2+BF2,
∴(k)2=(3k﹣x)2+x2,
整理得x2﹣3kx+2k2=0,
解得x=k或2k(舍弃),
∴AE=k,BE=2k,
∴=,
故答案为.
21.解:∵在△DBC和△BAC中
∠C=∠C,DBC=∠A
∴△DBC∽△BAC
∴==
∵=
∴==
设DC=2x,BC=3x,
则AC===
∴AD=AC﹣DC=﹣2x=x
∴==
故答案为:.
22.解:过A作AE⊥x轴,
∵△ABD是△COD关于点D的位似图形,
且△ABD与△COD的位似是1:3,
∴=,
∴OE=AB,
∴==.
假设BD=x,AB=y
∴DO=3x,AE=4x,CO=3y,
∵△ABD的面积为1,
∴xy=1,
∴xy=2,
∴AB AE=4xy=8,
即:k=4xy=8.
故答案是:8.
23.解:由题意得:△ABG∽△ADE,△ACF∽△ADE,
∴=,=,
∵AB=2cm,BC=3cm,CD=DE=4cm,
∴GB=(cm),FC=(cm),
∴S阴影=9﹣×(+)×3=(cm2)
故答案为
24.解:连接OP,交AB于点F,连接AC.
根据垂径定理的推论,得OP⊥AB,AF=BF.
根据90°的圆周角所对的弦是直径,则AC为直径.
设正方形的边长是1,则AC=,圆的半径是.
根据正方形的性质,得∠OAF=45°.
所以OF=,PF=.
∵OP∥AD,
∴==.
故答案为.
25.解:①由AB=AC,∠A=36°,得∠ABC=∠C=72°,
又BD平分∠ABC交AC于点D,
∴∠ABD=∠CBD=∠ABC=36°=∠A,
∴AD=BD,
∠BDC=∠ABD+∠A=72°=∠C,
∴BC=BD,
∴BC=BD=AD,
∴①正确;
②△ABD与△BCD在AC边上的高相等,
故△ABD与△BCD的面积比等于对应底边的比,
∴②正确;
③由①的条件可证△BCD∽△ACB,
则BC:AC=CD:BC,
∴BC2=CD AC,
∴③正确;
④设BC=x,则AC=AB=2,CD=AC﹣AD=2﹣x,
由BC2=CD AC,得x2=(2﹣x) 2,
解得x=±﹣1(舍去负值),
∴BC=﹣1,
∴④正确.
正确的有4个,
故答案为:4.
26.解:(1)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是(2,﹣2);
(2)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,
(3)四边形AA2C2C的面积是=;
故答案为:(1)(2,﹣2);(2)7.5
27.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵BE=BD,
∴∠BED=∠BDE.
∴∠AEB=∠ADC.
∴△ABE∽△ACD.
(2)解:∵△ABE∽△ACD,
∴.
∵BE=BD=1,CD=2,
∴.
28.解:(1)设矩形零件PQMN的边PN=a,PQ=x,则AE=80﹣a.
∵PN∥BC,∴△APN∽△ABC.
∴=.
因此,,
解得a=120﹣x.
∴120﹣x=x,
解得:x=48
所以长方形PQMN的面积S=xa=x(120﹣x)=﹣x2+120x=﹣×482+120×48=2304mm2
所以矩形零件PQMN的面积为2304mm2.
(2)由S=﹣x2+120x,
当x=﹣=40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2.
29.解:(1)∵CD⊥AB,AB是⊙O的直径
∴
∴∠AFC=∠ACD.
∵在△ACF和△AEC中,∠AFC=∠ACD,∠CAF=∠EAC
∴△AFC∽△ACE.
(2)∵四边形ACDF内接于⊙O
∴∠AFD+∠ACD=180°
∵∠AFD+∠DFE=180°
∴∠DFE=∠ACD
∵∠AFC=∠ACD
∴∠AFC=∠DFE.
∵△AFC∽△ACE
∴∠ACF=∠DEF.
∵F为的中点
∴AF=DF.
∵在△ACF和△DEF中,∠ACF=∠DEF,∠AFC=∠DFE,AF=DF
∴△ACF≌△DEF(AAS)
∴AC=DE=5
∵CD⊥AB,AB是⊙O的直径
∴CH=DH=3.
∴EH=8
在Rt△AHC中,AH2=AC2﹣CH2=16,
在Rt△AHE中,AE2=AH2+EH2=80,
∴.
∵△AFC∽△ACE
∴,即,
∴.
1.若=,则=( )
A. B. C. D.
2.如果用线段a、b、c,求作线段x,使a:b=c:x,那么下列作图正确的是( )
A. B.
C. D.
3.下列说法正确的个数有( )个
①凡正方形都相似;②凡等腰三角形都相似;
③凡等腰直角三角形都相似;
④两个相似多边形的面积比为4:9,则周长的比为16:81.
A.1 B.2 C.3 D.4
4.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么下列结论正确的是( )
A.DF= B.EF= C.CD= D.BF=
5.如果两个相似三角形的面积比是4:9,则它们对应边上的中线之比为( )
A.4:9 B.9:4 C.3:2 D.2:3
6.如图,在 ABCD中,E为CD边上的中点,AE交BD于点O,若S△DOE=2,则 ABCD的面积为( )
A.8 B.12 C.16 D.24
7.如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A. B.
C. D.
8.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC<BC,则下列结论中错误的是( )
A.CD2=AD DB B.AC DB=BC AD
C.AD BC=AC CD D.BC2=BD AB
9.我们把宽与长的比等于黄金比()的矩形称为黄金矩形.如图,在黄金矩形ABCD(AB<BC)中,∠ABC的平分线交AD边于点E,EF⊥BC于点F,则下列结论错误的是( )
A. B. C. D.
10.如图,A、B两地之间有一池塘,要测量A、B两地之间的距离.选择一点O,连接AO并延长到点C,使OC=AO,连接BO并延长到点D,使OD=BO.测得C、D间距离为30米,则A、B两地之间的距离为( )
A.30米 B.45米 C.60米 D.90米
11.如图,△ABC外任取一点O,连接AO、BO、CO,并取它们的中点D、E、F,得△DEF.下列说法正确的个数是( )
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;
③△ABC与△DEF周长之比为2:1;④△ABC与△DEF的面积之比为9:1.
A.1个 B.2个 C.3个 D.4个
12.如图,在△ABC中,高BD,CE相交于点F,图中与△BEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
13.如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=BC,连接GM.有如下结论:①DE=AF;②AN=AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.①②③ D.②③④
14.在坐标系中,已知A(6,0),B(0,8),C(0,﹣2),过点C作直线L交x轴于点D,使得以点D、C、O为顶点的三角形与△AOB相似,这样的直线一共可以作( )条.
A.3 B.4 C.5 D.6
15.如图,△ABD内接于⊙O,AB为⊙O的直径,C为弧AD的中点,CH⊥AB于点E,交AD于点P,交⊙O于点H,连接DH,连接BC交AD于点F.下列结论中:①DH⊥CB;②CP=PF;③CH=AD;④AP AD=CF CB;⑤若⊙O的半径为5,AF=,则CH=.正确的有( )
A.2个 B.3个 C.4个 D.5个
16.已知:=,那么= .
17.如图,四边形ABCD∽四边形A′B′C′D′,则边x= 、y= 、α= .
18.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,已知AB=25,BC=15,则BD= .
19.如图,小明与大树之间放置了一面平面镜,平面镜到小明的距离是2米、到大树的距离是6米时,小明恰好能从平面镜中看见大树的树尖,若小明的眼睛距离地面1.5米,则大树的高为 米.
20.如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为,则(AE<BE)的值为 .
21.如图,已知,在△ABC中,∠C=90°,点D是AC上一点,∠DBC=∠A,=,那么的值为 .
22.如图,A是反比例函数y=(x>0)图象上的一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则k的值为 .
23.将边长分别为2cm,3cm,4cm的三个正方形按如图所示的方式排列,则图中阴影部分的面积为 cm2.
24.如图,已知正方形ABCD的各个顶点A、B、C、D都在⊙O上,如果P是的中点,PD与AB交于E点,那么= .
25.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CD AC;④若AB=2,则BC=﹣1,其中正确的结论的个数是 个.
26.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.
27.如图,在△ABC中,AD平分∠BAC,E是AD上一点,且BE=BD.
(1)求证:△ABE∽△ACD;
(2)若BD=1,CD=2,求的值.
28.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上.
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
29.如图,AB是⊙O的直径,弦CD⊥AB于点H,点F是上一点,连接AF交CD的延长线于点E.
(1)求证:△AFC∽△ACE;
(2)若AC=5,DC=6,当点F为的中点时,求AF的值.
参考答案
1.解:=1+
∵=
∴=
把=代入=1+=
故选:C.
2.解:A、a:b=x:c与已知a:b=c:x不符合,故选项A不正确;
B、a:b=c:x与已知a:b=c:x符合,故选项B正确;
C、a:c=x:b与已知a:b=c:x不符合,故选项C不正确;
D、a:x=b:c与已知a:b=c:x不符合,故选项D不正确;
故选:B.
3.解:①凡正方形都相似,正确;
②等腰三角形两腰相等,对应成比例,但顶角不一定相等,所以不一定相似,故本小题错误;
③凡等腰直角三角形都相似,正确;
④两个相似多边形的面积比为4:9,则周长的比为2:3,故本小题错误;
所以,说法正确的有①③共2个.
故选:B.
4.解:∵AB∥CD∥EF,AC=2,AE=5,BD=1.5,
∴,
即,
解得:DF=,
∴BF=BD+DF=,
故选:D.
5.解:∵两个相似三角形的面积比是4:9,
∴两个相似三角形的相似比是2:3,
∴对应边上的中线的比为2:3,
故选:D.
6.解:∵四边形ABCD是平行四边形,E为CD边上的中点,
∴AB∥BC,DE=DC=AB,
∴△DOE∽△BOA,
∴===,=()2,即=,
∴S△BOA=8,S△AOD=4,
∴S△BAD=12,
∴ ABCD的面积=24,
故选:D.
7.解:A、根据平行线截得的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;
C、两三角形的对应角不一定相等,故两三角形不相似,故本选项符合题意;
D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项不符合题意.
故选:C.
8.解:∵∠ACB=90°,CD⊥AB
∴CD2=AD DB,BC2=BD AB,
故A、D选项正确;
∵△ACD∽△CBD,
∴==,
∴AC DB=BC CD,故B选项错误;
AD BC=AC CD,故C选项正确;
故选:B.
9.解:∵矩形ABCD(AB<BC)为黄金矩形,
∴设AB=﹣1,AD=2,
∵BF平分∠ABC,而∠ABC=90°,
∴四边形ABFE为正方形,
∴AE=AB,
∵DE=2﹣(﹣1)=3﹣
∴==,
而=,
∴=,所以A选项的结论正确;
∵==,=,
∴=,所以B选项的结论正确;
∵=,=,
∴≠,所以C选项的结论错误;
∵=,=,
∴=,所以D选项正确.
故选:C.
10.解:∵△ABO和△COD中,==,
且∠AOB=∠COD,
∴△AOB∽△COD,
∴=2,
又∵CD=30m,
∴AB=60m.
故选:C.
11.解:根据位似的定义可得:△ABC与△DEF是位似图形,也是相似图形,位似比是2:1,则周长的比是2:1,因而面积的比是4:1,故①②③正确,④错误.
故选:C.
12.解:∵BD⊥AC、CE⊥AB,
∴∠BDA=∠BDC=∠CEA=∠CEB=90°,
∵∠FBE=∠ABD,
∴△FBE∽△ABD,
∵∠BFE=∠CFD,
∴△BFE∽△CFD,
∵∠FCD=∠ACE,
∴△CFD∽△CAE,
∴△BFE∽△CAE,
综上,图中与△BEF相似的三角形有△BAD、△CFD、△CAE这3个,
故选:C.
13.解:∵四边形ABCD是正方形,
∴AD=AB=CD=BC,∠CDE=∠DAF=90°,
∵CE⊥DF,
∴∠DCE+∠CDF=∠ADF+∠CDF=90°,
∴∠ADF=∠DCE,
在△ADF与△DCE中,
,
∴△ADF≌△DCE(ASA),
∴DE=AF;故①正确;
∵AB∥CD,
∴=,
∵AF:FB=1:2,
∴AF:AB=AF:CD=1:3,
∴=,
∴=,
∵AC=AB,
∴=,
∴AN=AB;故②正确;
作GH⊥CE于H,设AF=DE=a,BF=2a,则AB=CD=BC=3a,EC=a,
∵∠DCE=∠DCM,∠CDE=∠CMD=90°,
∴△CMD∽△CDE,
∵∠DCE+∠DEC=∠DCE+∠HCG=90°,
∴∠DEC=∠HCG,
又∵∠CDE=∠CHG=90°,
∴△GHC∽△CDE,由△CMD∽△CDE,可得CM=a,
由△GHC∽△CDE,可得CH=a,
∴CH=MH=CM,
∵GH⊥CM,
∴GM=GC,
∴∠GMH=∠GCH,
∵∠FMG+∠GMH=90°,∠DCE+∠GCM=90°,
∴∠FMG=∠DCE,
∵∠ADF=∠DCE,
∴∠ADF=∠GMF;故③正确,
(补充方法:延长MF交CG的延长线于T,证明CG=GT,利用直角三角形斜边中线的性质即可解决问题)
设△ANF的面积为m,
∵AF∥CD,
∴==,△AFN∽△CDN,
∴△ADN的面积为3m,△DCN的面积为9m,
∴△ADC的面积=△ABC的面积=12m,
∴S△ANF:S四边形CNFB=1:11,故④错误,
故选:C.
14.解:若△AOB∽△COD,则==,
∴OD=,则D(,0)或(﹣,0).
若△AOB∽△DOC,则==,
∴OD=,则D(,0)或(﹣,0).
所以可以作出四条直线.
故选:B.
15.解:∵C为弧AD的中点,
∴=,
∴∠H=∠ABC,
∵CH⊥AB,
∴∠C+∠ABC=90°,
∴∠H+∠C=90°,
∴DH⊥BC,故①正确;
∵=,
∴∠CBD=∠ABC,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠BFD+∠DBF=90°,
∴∠C=∠BFD,
∵∠CFP=∠DFB,
∴∠C=∠CFP,
∴CP=PF,故②正确;
∵AB为⊙O的直径,C为弧AD的中点,CH⊥AB,
∴==,
∴=,
∴CH=AD;故③正确;
连接AC,BH,
则∠ACH=∠CAD,
∴AP=CP,
∵CH⊥AB,
∴=,
∴BC=BH,
∴∠BCH=∠BHC,
∴∠CFP=∠BHC,
∵∠PCF=∠BCH,
∴△CPF∽△CBH,
∴,
∴PC CH=CF CB,
∵PC=AP,CH=AD,
∴AP AD=CF CB,故④正确;
∵∠CAF=∠ABC,
又∵∠ACF=∠BCA,
∴△CAF∽△CBA,
∴===.
又∵AB=10,
∴AC=6,BC=8.
根据直角三角形的面积公式,得:AC BC=AB CE,
∴6×8=10CE.
∴CE=.
又∵CH=HE,
∴CH=2CE=.故⑤错误,
故选:C.
16.解:∵=,
∴设x=2a,y=3a,
∴==.
故答案为:.
17.解:∵四边形ABCD∽四边形A′B′C′D′,
∴==,∠C=α,∠D=∠D′=140°.
∴x=12,y=,α=∠C=360°﹣∠A﹣∠B﹣∠D=360°﹣62°﹣75°﹣140°=83°.
故答案为:12、、83°.
18.解:由射影定理得,BC2=BD AB,
∴BD==9,
故答案为:9.
19.解:根据题意可得:AB=1.5,AP=2,CP=6,∠BPA=∠DPC,∠A=∠C=90°,
∴△ABP∽△CDP,
∴=,
即:=,
∴CD=4.5(米),
故答案为:4.5.
20.解:∵正方形EFGH与正方形ABCD的相似比为,
∴不妨假设EF=k,AB=3k,
∵∠A=∠B=∠FEH=90°,
∴∠AEH+∠BEF=90°,∠BEF+∠EFB=90°,
∴∠AEH=∠EFB,
∵EH=EF,
∴△HAE≌△EBF(AAS),
∴AE=BF,设AE=BF=x则EB=3k﹣x,
在Rt△EFB中,∵EF2=BE2+BF2,
∴(k)2=(3k﹣x)2+x2,
整理得x2﹣3kx+2k2=0,
解得x=k或2k(舍弃),
∴AE=k,BE=2k,
∴=,
故答案为.
21.解:∵在△DBC和△BAC中
∠C=∠C,DBC=∠A
∴△DBC∽△BAC
∴==
∵=
∴==
设DC=2x,BC=3x,
则AC===
∴AD=AC﹣DC=﹣2x=x
∴==
故答案为:.
22.解:过A作AE⊥x轴,
∵△ABD是△COD关于点D的位似图形,
且△ABD与△COD的位似是1:3,
∴=,
∴OE=AB,
∴==.
假设BD=x,AB=y
∴DO=3x,AE=4x,CO=3y,
∵△ABD的面积为1,
∴xy=1,
∴xy=2,
∴AB AE=4xy=8,
即:k=4xy=8.
故答案是:8.
23.解:由题意得:△ABG∽△ADE,△ACF∽△ADE,
∴=,=,
∵AB=2cm,BC=3cm,CD=DE=4cm,
∴GB=(cm),FC=(cm),
∴S阴影=9﹣×(+)×3=(cm2)
故答案为
24.解:连接OP,交AB于点F,连接AC.
根据垂径定理的推论,得OP⊥AB,AF=BF.
根据90°的圆周角所对的弦是直径,则AC为直径.
设正方形的边长是1,则AC=,圆的半径是.
根据正方形的性质,得∠OAF=45°.
所以OF=,PF=.
∵OP∥AD,
∴==.
故答案为.
25.解:①由AB=AC,∠A=36°,得∠ABC=∠C=72°,
又BD平分∠ABC交AC于点D,
∴∠ABD=∠CBD=∠ABC=36°=∠A,
∴AD=BD,
∠BDC=∠ABD+∠A=72°=∠C,
∴BC=BD,
∴BC=BD=AD,
∴①正确;
②△ABD与△BCD在AC边上的高相等,
故△ABD与△BCD的面积比等于对应底边的比,
∴②正确;
③由①的条件可证△BCD∽△ACB,
则BC:AC=CD:BC,
∴BC2=CD AC,
∴③正确;
④设BC=x,则AC=AB=2,CD=AC﹣AD=2﹣x,
由BC2=CD AC,得x2=(2﹣x) 2,
解得x=±﹣1(舍去负值),
∴BC=﹣1,
∴④正确.
正确的有4个,
故答案为:4.
26.解:(1)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是(2,﹣2);
(2)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,
(3)四边形AA2C2C的面积是=;
故答案为:(1)(2,﹣2);(2)7.5
27.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵BE=BD,
∴∠BED=∠BDE.
∴∠AEB=∠ADC.
∴△ABE∽△ACD.
(2)解:∵△ABE∽△ACD,
∴.
∵BE=BD=1,CD=2,
∴.
28.解:(1)设矩形零件PQMN的边PN=a,PQ=x,则AE=80﹣a.
∵PN∥BC,∴△APN∽△ABC.
∴=.
因此,,
解得a=120﹣x.
∴120﹣x=x,
解得:x=48
所以长方形PQMN的面积S=xa=x(120﹣x)=﹣x2+120x=﹣×482+120×48=2304mm2
所以矩形零件PQMN的面积为2304mm2.
(2)由S=﹣x2+120x,
当x=﹣=40时,a=60.
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2.
29.解:(1)∵CD⊥AB,AB是⊙O的直径
∴
∴∠AFC=∠ACD.
∵在△ACF和△AEC中,∠AFC=∠ACD,∠CAF=∠EAC
∴△AFC∽△ACE.
(2)∵四边形ACDF内接于⊙O
∴∠AFD+∠ACD=180°
∵∠AFD+∠DFE=180°
∴∠DFE=∠ACD
∵∠AFC=∠ACD
∴∠AFC=∠DFE.
∵△AFC∽△ACE
∴∠ACF=∠DEF.
∵F为的中点
∴AF=DF.
∵在△ACF和△DEF中,∠ACF=∠DEF,∠AFC=∠DFE,AF=DF
∴△ACF≌△DEF(AAS)
∴AC=DE=5
∵CD⊥AB,AB是⊙O的直径
∴CH=DH=3.
∴EH=8
在Rt△AHC中,AH2=AC2﹣CH2=16,
在Rt△AHE中,AE2=AH2+EH2=80,
∴.
∵△AFC∽△ACE
∴,即,
∴.
