1.3位置变化快慢的描述-速度 课件(共23张PPT)
文档属性
| 名称 | 1.3位置变化快慢的描述-速度 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-11 13:10:15 | ||
图片预览








文档简介
(共23张PPT)
1.3 位置变化快慢的描述
——速度
第一章
运动的描述
运行中的高铁
飞行的国产大飞机
航行中的客轮
改装的牛车
【新课导入】
生活和科学研究中经常需要知道物体运动的快慢和方向,你还记得初中是怎样描述物体运动快慢的吗?运动员在比赛中的不同时段,运动的快慢一样吗?
2、在百米赛跑中,如何比较运动员跑得快慢?
结论:相等位移内经过的时间不同
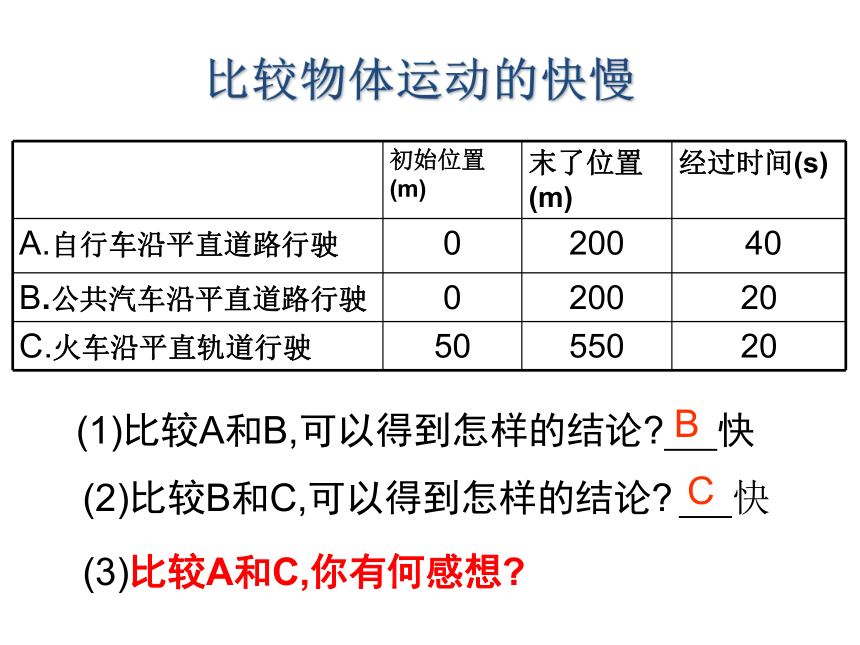
初始位置 (m) 末了位置(m) 经过时间(s)
A.自行车沿平直道路行驶 0 200 40
B.公共汽车沿平直道路行驶 0 200 20
C.火车沿平直轨道行驶 50 550 20
(1)比较A和B,可以得到怎样的结论 快
(2)比较B和C,可以得到怎样的结论 快
(3)比较A和C,你有何感想
B
C
比较物体运动的快慢
对于A和C,位移不同,时间也不同,如何比较快慢?
办法:以单位时间作为标准,比较在单位时间内的位移。
结论:可以用单位时间内的位移来描述物体运动的快慢。
一.速度
2.符号:v
3.定义式:
4.单位及其换算:
m/s km/h
1m/s=3.6km/h
△x 越大,v越大吗?
1.定义:位移与发生这个位移所用时间的比值。
国际单位制为m/s(或m s-1 )
定义理解
1、速度的大小与位移成正比对吗?请举例说明。
2、速度的大小与时间成反比对吗?请举例说明。
——比值法定义
匀速直线运动
匀速直线运动:
物体在一条直线上运动,如果在相等的时间里位移相等,这种运动叫做匀速直线运动.
(1)匀速直线运动的轨迹是直线
(2)“匀速”是指任何相等的时间内位移都相等.
匀速直线速度
实质:是一种快慢不变(V的大小方向都不变)的运动。
两辆汽车从某地出发,速度都是20m/s,他们的运动情况完全相同吗?
—— 可能是背道而驰 !!
体会:速度仅指出大小是不够的,还必须具有______
方向
速度是___量
矢
方向:与物体的运动方向相同。
平均速度
1 .平均速度
物体运动的位移与发生这个位移所用的时间的比值,叫做平均速度
2. 物理意义
3. 定义式
粗略地描述了物体运动快慢程度平均速度大,物体运动快,反之慢
4. 单位
m/s
一辆自行车在第一个5s内的位移为10m,第二个5s内的位移为15m,第三个5s内的位移为12m,请分别求出它在每个5s内的平均速度以及这15s内的平均速度
v1=2m/s;v2=3m/s;v3=2.4m/s;v=2.47m/s
5. 计算物体的平均速度时要注意哪些问题
说明:平均速度只是对运动物体在某一段时间内
(或某一段位移内)而言的,对同一运动物体,在不同的过程,它的平均速度可能是不同的,因此,平均速度必须指明“哪段时间”或“哪段位移”的.
问题:一个运动员在百米赛跑中,50 m处的速度是6 m/s,16 s末到达终点时的速度为7.5 m/s,则整个赛跑过程中他的平均速度的大小是( )
A.6m/s B.6.25 m/s
C.6.75m/s D.7.5 m/s
B
解题心得:平均速度
不等于速度的平均
2、瞬时速度:
物体在某一时刻(位置)时的速度
问题:
我们怎样才能知道物体运动的瞬时速度呢?
物理意义:精确描述某个时刻(或对应位置)的实际运动快慢程度。
在公式 中,如果时间 非常小, 接近于零,表示的是某一瞬间,这时的速度称为
极限思想
探究
瞬时速度
瞬时速度
关于瞬时速度的几点理解
1. 瞬时速度是精确地描述物体运动快慢的物理量
2. 瞬时速度是矢量,其方向即为物体运动方向
3. 可以用一个较短时间内的平均速度来替代瞬时速度
4. 瞬时速度的大小称之为速率
2.速率:
(1)定义:瞬时速度的大小
(2)是___量
(3)汽车的速度计显示的是 _____
3.常说的“速度”,可能指:
“平均速度”、“瞬时速度”或“速率”
速率
标
1.速率:
(1)定义:瞬时速度的大小
(2)是___量
(3)汽车的速度计显示的是 _____
2.常说的“速度”,可能指:
“平均速度”、“瞬时速度”或“速率”
速率
标
速率
平均速率是平均速度的大小吗
匀速直线运动平均速度的大小与平均速率是否相等
平均速率:路程与时间的比值。
1.下列日常生活中所说的速度平均速度还是瞬时速度
A、一辆汽车在高速公路上行驶的速度约100km/h
B、汽车在高速公路行驶的最大速度限制120km/h
C、声音的传播速度是340m/s
D、刘翔以9.4m/s的速度冲过终点线
小试牛刀
2.一辆汽车从甲地直线开往乙地的过程中,前一半位移的平均速度是30 km/h,后一半位移的平均速度是60 km/h.则在全程内这辆汽车的平均速度是________.
40km/h
牛
刀
小
试
3.一辆汽车从甲地开往乙地的过程中,前一半时间内的平均速度是30 km/h,后一半时间的平均速度是60 km/h.则在全程内这辆汽车的平均速度是________.
45km/h
牛
刀
小
试
再见!
1.3 位置变化快慢的描述
——速度
第一章
运动的描述
运行中的高铁
飞行的国产大飞机
航行中的客轮
改装的牛车
【新课导入】
生活和科学研究中经常需要知道物体运动的快慢和方向,你还记得初中是怎样描述物体运动快慢的吗?运动员在比赛中的不同时段,运动的快慢一样吗?
2、在百米赛跑中,如何比较运动员跑得快慢?
结论:相等位移内经过的时间不同
初始位置 (m) 末了位置(m) 经过时间(s)
A.自行车沿平直道路行驶 0 200 40
B.公共汽车沿平直道路行驶 0 200 20
C.火车沿平直轨道行驶 50 550 20
(1)比较A和B,可以得到怎样的结论 快
(2)比较B和C,可以得到怎样的结论 快
(3)比较A和C,你有何感想
B
C
比较物体运动的快慢
对于A和C,位移不同,时间也不同,如何比较快慢?
办法:以单位时间作为标准,比较在单位时间内的位移。
结论:可以用单位时间内的位移来描述物体运动的快慢。
一.速度
2.符号:v
3.定义式:
4.单位及其换算:
m/s km/h
1m/s=3.6km/h
△x 越大,v越大吗?
1.定义:位移与发生这个位移所用时间的比值。
国际单位制为m/s(或m s-1 )
定义理解
1、速度的大小与位移成正比对吗?请举例说明。
2、速度的大小与时间成反比对吗?请举例说明。
——比值法定义
匀速直线运动
匀速直线运动:
物体在一条直线上运动,如果在相等的时间里位移相等,这种运动叫做匀速直线运动.
(1)匀速直线运动的轨迹是直线
(2)“匀速”是指任何相等的时间内位移都相等.
匀速直线速度
实质:是一种快慢不变(V的大小方向都不变)的运动。
两辆汽车从某地出发,速度都是20m/s,他们的运动情况完全相同吗?
—— 可能是背道而驰 !!
体会:速度仅指出大小是不够的,还必须具有______
方向
速度是___量
矢
方向:与物体的运动方向相同。
平均速度
1 .平均速度
物体运动的位移与发生这个位移所用的时间的比值,叫做平均速度
2. 物理意义
3. 定义式
粗略地描述了物体运动快慢程度平均速度大,物体运动快,反之慢
4. 单位
m/s
一辆自行车在第一个5s内的位移为10m,第二个5s内的位移为15m,第三个5s内的位移为12m,请分别求出它在每个5s内的平均速度以及这15s内的平均速度
v1=2m/s;v2=3m/s;v3=2.4m/s;v=2.47m/s
5. 计算物体的平均速度时要注意哪些问题
说明:平均速度只是对运动物体在某一段时间内
(或某一段位移内)而言的,对同一运动物体,在不同的过程,它的平均速度可能是不同的,因此,平均速度必须指明“哪段时间”或“哪段位移”的.
问题:一个运动员在百米赛跑中,50 m处的速度是6 m/s,16 s末到达终点时的速度为7.5 m/s,则整个赛跑过程中他的平均速度的大小是( )
A.6m/s B.6.25 m/s
C.6.75m/s D.7.5 m/s
B
解题心得:平均速度
不等于速度的平均
2、瞬时速度:
物体在某一时刻(位置)时的速度
问题:
我们怎样才能知道物体运动的瞬时速度呢?
物理意义:精确描述某个时刻(或对应位置)的实际运动快慢程度。
在公式 中,如果时间 非常小, 接近于零,表示的是某一瞬间,这时的速度称为
极限思想
探究
瞬时速度
瞬时速度
关于瞬时速度的几点理解
1. 瞬时速度是精确地描述物体运动快慢的物理量
2. 瞬时速度是矢量,其方向即为物体运动方向
3. 可以用一个较短时间内的平均速度来替代瞬时速度
4. 瞬时速度的大小称之为速率
2.速率:
(1)定义:瞬时速度的大小
(2)是___量
(3)汽车的速度计显示的是 _____
3.常说的“速度”,可能指:
“平均速度”、“瞬时速度”或“速率”
速率
标
1.速率:
(1)定义:瞬时速度的大小
(2)是___量
(3)汽车的速度计显示的是 _____
2.常说的“速度”,可能指:
“平均速度”、“瞬时速度”或“速率”
速率
标
速率
平均速率是平均速度的大小吗
匀速直线运动平均速度的大小与平均速率是否相等
平均速率:路程与时间的比值。
1.下列日常生活中所说的速度平均速度还是瞬时速度
A、一辆汽车在高速公路上行驶的速度约100km/h
B、汽车在高速公路行驶的最大速度限制120km/h
C、声音的传播速度是340m/s
D、刘翔以9.4m/s的速度冲过终点线
小试牛刀
2.一辆汽车从甲地直线开往乙地的过程中,前一半位移的平均速度是30 km/h,后一半位移的平均速度是60 km/h.则在全程内这辆汽车的平均速度是________.
40km/h
牛
刀
小
试
3.一辆汽车从甲地开往乙地的过程中,前一半时间内的平均速度是30 km/h,后一半时间的平均速度是60 km/h.则在全程内这辆汽车的平均速度是________.
45km/h
牛
刀
小
试
再见!
