华东师大版九年级数学下册 26.3 实践与探索课件(共23张PPT)
文档属性
| 名称 | 华东师大版九年级数学下册 26.3 实践与探索课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 348.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 20:38:53 | ||
图片预览







文档简介
(共23张PPT)
26.3 实践与探索(3)
学习目标
1.能利用两个函数图象求方程或方程组的解.(重点)
2.能利用两个函数的图象,求不等式的解集.(重点)
3.通过研究函数图象与方程(组)的解和不等式的解集,联系体会数形结合思想的应用.
复习引入
1.已知一次函数y=ax+b的图象经过A(2,0),B(0,-1)两点,则关于x的一元一次方程ax+b=0的解为_________;关于x的一元一次不等式ax+b≤0的解集为_________.
x=2
x≤2
1
1
2
x
y
A
B
1
1
2
y2
y1
x
y
A
B
C
2.已知一次函数y1=ax+b的图象经过A(2,0),B(0,-1)两点,y2=kx+c的图象经过A(2,0),C(0,2)两点,则关于x、y的二元一次方程组
关于x的一元一次不等式ax+b≤kx+c的解集为_________.
的解为_______;
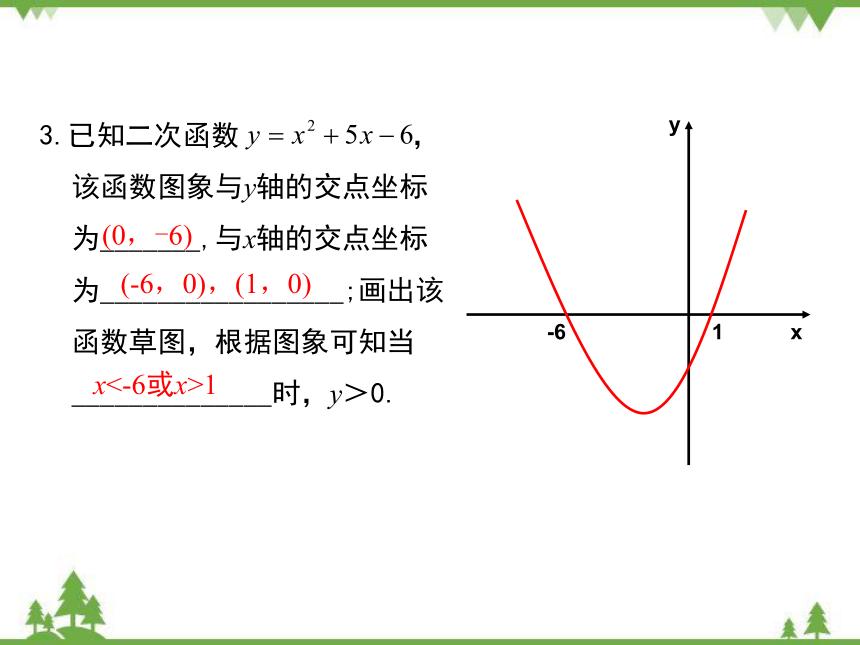
3.已知二次函数 ,该函数图象与y轴的交点坐标为_______,与x轴的交点坐标为_________________;画出该函数草图,根据图象可知当______________时,y>0.
x
-6
1
y
(0,-6)
(-6,0),(1,0)
x<-6或x>1
-4
2
x
y
x1=-4,x2=2
x<-4或x>2
-1
x>-1
4.已知二次函数 的图象如图所示,则一元二次方程 的解为___________;当____________时y<0;当__________时y随x的增大而减小.
利用两个函数图象求方程或方程组的解
合作探究
x
y
k2
k1
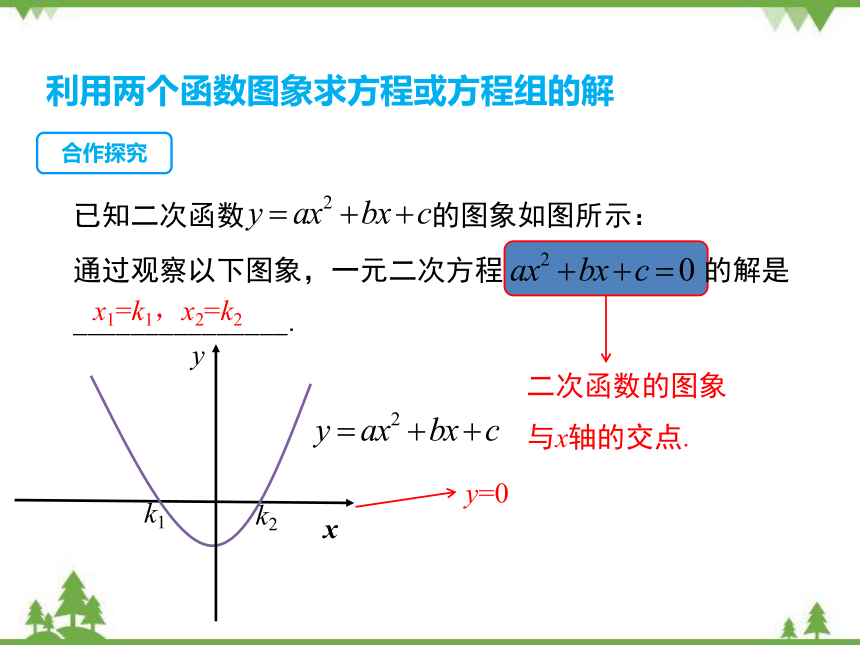
已知二次函数 的图象如图所示:
通过观察以下图象,一元二次方程 的解是_______________.
x1=k1,x2=k2
二次函数的图象与x轴的交点.
y=0
(x2, h)
x
y
k2
k1
问题1 二次函数 的图象与x轴(直线y=0)的交点的横坐标是一元二次方程 的根,那么,二次函数 与直线y=h的交点的横坐标是否也是某一个一元二次方程的根呢?
这个点的坐标有几种表示方式?
方程 的实数根.
x
y
x1
x2
问题2 如图,二次函数 的图象与一次函数 的图象交于两点,观察以下图象,你能得到哪些信息?
x1 , x2 可以看做是方程 的解.
(x1,y1 ), (x2,y2 ) 也可以看做是方程组 的解.
2
x
y
-2
0
4
-2
-4
-4
-6
-8
例1 利用二次函数的图象求一元二次方程x2+2x-1=3的近似根.
解:(1)原方程可变形为x2+2x-4=0;
(3)观察估计抛物线y=x2+2x-4和x轴的交点的横坐标;
(2)用描点法作二次函数y=x2+2x-4的图象;
由图象可知,它们有两个交点,其横坐标一个在-4与-3之间,另一个在1与2之间,分别约为-3.2和1.2.
(4)由此可知,一元二次方程x2+2x-1=3的近似根为:x1≈3.2,x2≈1.2.
想一想:还有没有别的办法求这个方程的近似根?
(1)用描点法作二次函数y=x2+2x-1的图象;
(3)观察估计抛物线y=x2+2x-1和直线y=3的交点的横坐标;
(2) 作直线y=3;
方法二:
2
x
y
2
4
4
-2
-4
0
-2
-4
由图象可知,它们有两个交点,其横坐标一个在-4与-3之间,另一个在1与2之间,分别约为-3.2和1.2.
(4)由此可知,一元二次方程x2+2x-1=3的近似根为x1≈3.2,x2≈1.2.
方法三:
(1)作二次函数y=x2的图象;
(2)作一次函数y=-2x+4的图象;
(3)观察估计抛物线y=x2+2x-1和直线y=3的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-4与-3之间,另一个在1与2之间,分别约为-3.2和1.2.
(4)由此可知,一元二次方程x2+2x-1=3的近似根为x1≈3.2,x2≈1.2.
2
x
y
2
4
4
-2
-4
o
-2
两个函数图象的交点坐标就是对应函数解析式所组成的方程组的解.
函数解析式对应方程的根,就是该应函数图象与x轴交点的横坐标;
归纳
利用两个函数图象求不等式的解集
典例精析
例2 已知抛物线 (a>0)与直线 相交于点O(0,0)和点A(3,2),求不等式 的解集.
分析:根据题目提供的条件,无法求出抛物线的解析式.因此,我们可以换一个思路,利用函数的图象来判求不等式的解集.
解:根据题目提供的条件,画出草图:
x
y
O
3
2
由图可知,不等式 的解集为 或 .
方法归纳
不等式 的解集是二次函数
的图象在直线 上方的点的横坐标所组成的范围.
不等式 的解集是二次函数
的图象在直线 下方的点的横坐标所组成的范
已知函数y1=x2与函数 的图象大致如图,若
y1<y2,则自变量x的取值范围是( )
做一做
A.
C.
B. 或
D. 或
C
解析:先根据方程 算出图象交点的横坐标,然后再结合图象,得出答案.
1.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
A.x1=0,x2=4 B.x1=1,x2=5 C.x1=1,x2=-5 D.x1=-1,x2=5
2.若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=-1,则使函数值y>0成立的x的取值范围是( )
A.x<-4或x>2 B.-4≤x≤2 C.x≤-4或x≥2 D.-4<x<2
D
D
练 习
3.二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象如图所示,则方程ax2+bx+c=m有实数根的条件是( )
A.m≥-2 B.m≥5 C.m≥0 D.m≥4
解析:方程ax2+bx+c=m有实数根,即表示二次函数y=ax2+bx+c的图象与直线y=m有交点.
A
4.如图,一次函数y1=kx+1与二次函数y2=ax2+bx-2交于A、B两点,且A(1,0),抛物线的对称轴是 .
(1) 求k和a、b的值;
(2)求不等式 kx+1>ax2+bx-2的解集.
x
y
A
O
B
解:(1)y1=kx+1经过点A(1,0),则0=k+1,得k=-1.
y=ax2+bx-2经过点A(1,0),则
0=a+b-2 ①,抛物线的对称轴是 ,故 ② ,
联立① ②,解得
(2)根据对称性,可知y2道与x轴的另一个交点为(-4,0),
根据图象可以看出,kx+1>ax2+bx-2的解集为-4<x<1.
变 形
函数图象交点的横坐标
变 形
函数图象交点的横坐标
变 形
变 形
解集是抛物线图象在直线下方的点的横坐标所组成的取值范围
解集是抛物线图象在直线上方的点的横坐标所组成的取值范围
小 结
26.3 实践与探索(3)
学习目标
1.能利用两个函数图象求方程或方程组的解.(重点)
2.能利用两个函数的图象,求不等式的解集.(重点)
3.通过研究函数图象与方程(组)的解和不等式的解集,联系体会数形结合思想的应用.
复习引入
1.已知一次函数y=ax+b的图象经过A(2,0),B(0,-1)两点,则关于x的一元一次方程ax+b=0的解为_________;关于x的一元一次不等式ax+b≤0的解集为_________.
x=2
x≤2
1
1
2
x
y
A
B
1
1
2
y2
y1
x
y
A
B
C
2.已知一次函数y1=ax+b的图象经过A(2,0),B(0,-1)两点,y2=kx+c的图象经过A(2,0),C(0,2)两点,则关于x、y的二元一次方程组
关于x的一元一次不等式ax+b≤kx+c的解集为_________.
的解为_______;
3.已知二次函数 ,该函数图象与y轴的交点坐标为_______,与x轴的交点坐标为_________________;画出该函数草图,根据图象可知当______________时,y>0.
x
-6
1
y
(0,-6)
(-6,0),(1,0)
x<-6或x>1
-4
2
x
y
x1=-4,x2=2
x<-4或x>2
-1
x>-1
4.已知二次函数 的图象如图所示,则一元二次方程 的解为___________;当____________时y<0;当__________时y随x的增大而减小.
利用两个函数图象求方程或方程组的解
合作探究
x
y
k2
k1
已知二次函数 的图象如图所示:
通过观察以下图象,一元二次方程 的解是_______________.
x1=k1,x2=k2
二次函数的图象与x轴的交点.
y=0
(x2, h)
x
y
k2
k1
问题1 二次函数 的图象与x轴(直线y=0)的交点的横坐标是一元二次方程 的根,那么,二次函数 与直线y=h的交点的横坐标是否也是某一个一元二次方程的根呢?
这个点的坐标有几种表示方式?
方程 的实数根.
x
y
x1
x2
问题2 如图,二次函数 的图象与一次函数 的图象交于两点,观察以下图象,你能得到哪些信息?
x1 , x2 可以看做是方程 的解.
(x1,y1 ), (x2,y2 ) 也可以看做是方程组 的解.
2
x
y
-2
0
4
-2
-4
-4
-6
-8
例1 利用二次函数的图象求一元二次方程x2+2x-1=3的近似根.
解:(1)原方程可变形为x2+2x-4=0;
(3)观察估计抛物线y=x2+2x-4和x轴的交点的横坐标;
(2)用描点法作二次函数y=x2+2x-4的图象;
由图象可知,它们有两个交点,其横坐标一个在-4与-3之间,另一个在1与2之间,分别约为-3.2和1.2.
(4)由此可知,一元二次方程x2+2x-1=3的近似根为:x1≈3.2,x2≈1.2.
想一想:还有没有别的办法求这个方程的近似根?
(1)用描点法作二次函数y=x2+2x-1的图象;
(3)观察估计抛物线y=x2+2x-1和直线y=3的交点的横坐标;
(2) 作直线y=3;
方法二:
2
x
y
2
4
4
-2
-4
0
-2
-4
由图象可知,它们有两个交点,其横坐标一个在-4与-3之间,另一个在1与2之间,分别约为-3.2和1.2.
(4)由此可知,一元二次方程x2+2x-1=3的近似根为x1≈3.2,x2≈1.2.
方法三:
(1)作二次函数y=x2的图象;
(2)作一次函数y=-2x+4的图象;
(3)观察估计抛物线y=x2+2x-1和直线y=3的交点的横坐标;
由图象可知,它们有两个交点,其横坐标一个在-4与-3之间,另一个在1与2之间,分别约为-3.2和1.2.
(4)由此可知,一元二次方程x2+2x-1=3的近似根为x1≈3.2,x2≈1.2.
2
x
y
2
4
4
-2
-4
o
-2
两个函数图象的交点坐标就是对应函数解析式所组成的方程组的解.
函数解析式对应方程的根,就是该应函数图象与x轴交点的横坐标;
归纳
利用两个函数图象求不等式的解集
典例精析
例2 已知抛物线 (a>0)与直线 相交于点O(0,0)和点A(3,2),求不等式 的解集.
分析:根据题目提供的条件,无法求出抛物线的解析式.因此,我们可以换一个思路,利用函数的图象来判求不等式的解集.
解:根据题目提供的条件,画出草图:
x
y
O
3
2
由图可知,不等式 的解集为 或 .
方法归纳
不等式 的解集是二次函数
的图象在直线 上方的点的横坐标所组成的范围.
不等式 的解集是二次函数
的图象在直线 下方的点的横坐标所组成的范
已知函数y1=x2与函数 的图象大致如图,若
y1<y2,则自变量x的取值范围是( )
做一做
A.
C.
B. 或
D. 或
C
解析:先根据方程 算出图象交点的横坐标,然后再结合图象,得出答案.
1.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
A.x1=0,x2=4 B.x1=1,x2=5 C.x1=1,x2=-5 D.x1=-1,x2=5
2.若二次函数y=ax2+bx+c(a<0)的图象经过点(2,0),且其对称轴为x=-1,则使函数值y>0成立的x的取值范围是( )
A.x<-4或x>2 B.-4≤x≤2 C.x≤-4或x≥2 D.-4<x<2
D
D
练 习
3.二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象如图所示,则方程ax2+bx+c=m有实数根的条件是( )
A.m≥-2 B.m≥5 C.m≥0 D.m≥4
解析:方程ax2+bx+c=m有实数根,即表示二次函数y=ax2+bx+c的图象与直线y=m有交点.
A
4.如图,一次函数y1=kx+1与二次函数y2=ax2+bx-2交于A、B两点,且A(1,0),抛物线的对称轴是 .
(1) 求k和a、b的值;
(2)求不等式 kx+1>ax2+bx-2的解集.
x
y
A
O
B
解:(1)y1=kx+1经过点A(1,0),则0=k+1,得k=-1.
y=ax2+bx-2经过点A(1,0),则
0=a+b-2 ①,抛物线的对称轴是 ,故 ② ,
联立① ②,解得
(2)根据对称性,可知y2道与x轴的另一个交点为(-4,0),
根据图象可以看出,kx+1>ax2+bx-2的解集为-4<x<1.
变 形
函数图象交点的横坐标
变 形
函数图象交点的横坐标
变 形
变 形
解集是抛物线图象在直线下方的点的横坐标所组成的取值范围
解集是抛物线图象在直线上方的点的横坐标所组成的取值范围
小 结
