沪科版数学七年级上册第1章有理数-规律探索课件(共27张PPT)
文档属性
| 名称 | 沪科版数学七年级上册第1章有理数-规律探索课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 276.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 20:44:01 | ||
图片预览







文档简介
(共27张PPT)
第1章 有理数(通用)
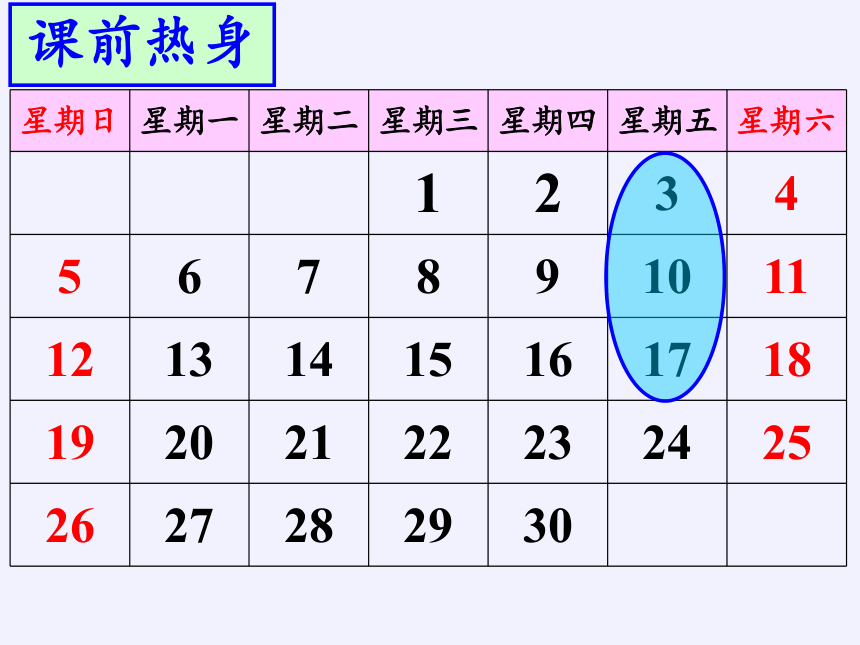
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30
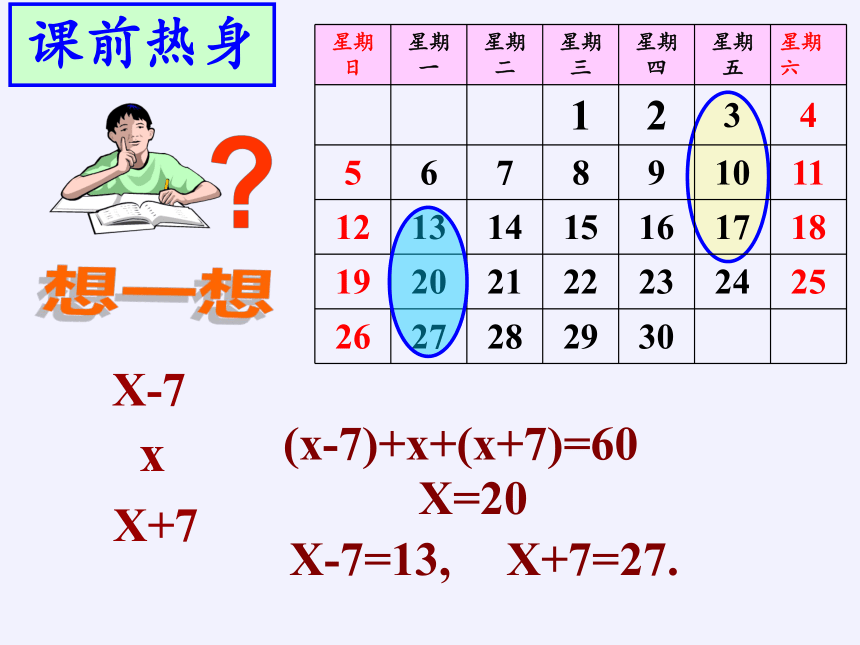
课前热身
(x-7)+x+(x+7)=60
X=20
X-7=13,
X+7=27.
x
X-7
X+7
想一想
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30
课前热身
2017年4月
课前热身
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30
许多事物都存在着一定的规律性,只要我们善于观察、勤于思考,就可以发现它们,并利用它们来丰富我们的生活。
找规律
一、数字规律
请你按照如下的数字规律,分别写出第n个数字:(n为正整数)
例1
(1)2,4,6,8,10, … , ____;
(2)1,3,5,7,9, … , ____;
(4)2,4,8,16,32,… , ____;
2n
2n-1
2n
(3)3,5,7,9,11,…, ____;
2n+1
① ② ③ ④ ⑤
n
(5)-1,1,-1,1,-1,...,_______。
(-1)n
3.验证所归纳的结论。
回忆一下:
2.猜想规律与“序号n”间的对应关系。
关于寻找“数字序列”规律的思维步骤:
1.观察相邻数字间的共同规律。
(1) 3,6,9,12, 15,… , ____;
(2) 2,5,8,11, 14, … , ____;
请你按照如下的数字规律,分别写出第n个数字:(n为正整数)
3n
3n-1
练一练
(3) 3,9,27, 81,… , ____ ;
3n
(4) 1,-1,1,-1,1,...,_______.
(-1)n-1
中考练兵
请先观察下列算式,再填空:
32-12=8×1,
52-32=8×2,
72-52=8×__ ,
92-( )2 =8×4,
( )2-92 =8×5,
132_( )2=8×( ),…… ,
通过观察归纳,写出反映这种规律的一般结论:
(2n+1)2-(2n-1)2=8n
3
7
11
11
6
例2
观察下列排列的等式:
1×2-1=12,
2×3-2=22,
3×4-3=32,
4×5-4=42,…….
猜想:第n个等式(n为正整数)
应为________________.
n(n+1)-n=n2
练一练
二、图形规律
例3 餐桌按下面的摆法可坐多少人
(2) 若按照上图的摆法摆放餐桌和椅子,完成下表:
(1) 1张餐桌可坐6人,2张餐桌可坐___人.
桌子张数 1 2 3 4 5 6 … n
可坐人数 6 10 …
10
14
18
4n+2
22
26
3.验证所归纳的结论。
回忆一下:
2.猜想规律与“序号n”间的对应关系。
关于寻找“图形序列”规律的思维步骤:
1.观察图形的排列规律找到基本图形,找到图形之间的变与不变的规律。
例4 联体长方形的摆法:(填空)
(1)如图,摆n个这样联体图形需 根火柴;
(2)如图,摆n个这样联体图形需 根火柴;
3n+1
5n+2
(3)如图,摆n个这样的联体图形需_______火柴;
(4)如图,摆n个这样联体图形需______根火柴.
7n+3
9n+4
练习
1.用红白两种颜色的正方形纸片,按红色纸片数逐一增加的规律拼成一列图案:
第一图
第二图
第三图
……
(1)第4个图案中,白色纸片一共有___张;
(2)第n个图案中,白色纸片一共有_____ 张;
3n+1
13
2.用黑白两种颜色的正方形纸片,按黑色纸片数逐一增加的规律拼成一列图案,第五个图案中,白色正方形的个数一共有_____个.
28
第一个
第二个
第三个
……
3.(湖南湘潭)为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:
按照上面的规律,摆个“金鱼”需用火柴棒的根数为( )
A.6n+2 B.6n+8
C.8n D.4n+4
A
4.如图所示,用火柴拼成一排由三角形组成的图形,如果要使图形中含有50个三角形,那么需要火柴( )
A.100根 B.101根
C.150根 D.153根
含有n个三角形需要( )根火柴
B
2n+1
5.如下图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n个小房子用了______________ 块石子.
(n+1)2+(2n-1)
(1)
(2)
(3)
(4)
3.验证所归纳的结论。
课堂小结
2.猜想规律与“序号”间的对应关系,用关于“序号”的数学式子表示出来。
一.关于寻找“数字序列”规律的思维步骤:
1.观察相邻数字间的数量关系,找到共同特征,得出某种规律的猜想。
3.验证所归纳的结论。
2.猜想规律与“序号”间的对应关系,用关于“序号”的数学式子表示出来。
二.关于寻找“图形序列”规律的思维步骤:
1.观察图形的排列规律找到基本图形,找到图形之间的变与不变的规律。
课堂小结
课堂小结
通过这节课的学习,你在思考问题的方法上,有哪些收获?
3n+2
14
课堂反馈
谢 谢
第1章 有理数(通用)
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30
课前热身
(x-7)+x+(x+7)=60
X=20
X-7=13,
X+7=27.
x
X-7
X+7
想一想
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30
课前热身
2017年4月
课前热身
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30
许多事物都存在着一定的规律性,只要我们善于观察、勤于思考,就可以发现它们,并利用它们来丰富我们的生活。
找规律
一、数字规律
请你按照如下的数字规律,分别写出第n个数字:(n为正整数)
例1
(1)2,4,6,8,10, … , ____;
(2)1,3,5,7,9, … , ____;
(4)2,4,8,16,32,… , ____;
2n
2n-1
2n
(3)3,5,7,9,11,…, ____;
2n+1
① ② ③ ④ ⑤
n
(5)-1,1,-1,1,-1,...,_______。
(-1)n
3.验证所归纳的结论。
回忆一下:
2.猜想规律与“序号n”间的对应关系。
关于寻找“数字序列”规律的思维步骤:
1.观察相邻数字间的共同规律。
(1) 3,6,9,12, 15,… , ____;
(2) 2,5,8,11, 14, … , ____;
请你按照如下的数字规律,分别写出第n个数字:(n为正整数)
3n
3n-1
练一练
(3) 3,9,27, 81,… , ____ ;
3n
(4) 1,-1,1,-1,1,...,_______.
(-1)n-1
中考练兵
请先观察下列算式,再填空:
32-12=8×1,
52-32=8×2,
72-52=8×__ ,
92-( )2 =8×4,
( )2-92 =8×5,
132_( )2=8×( ),…… ,
通过观察归纳,写出反映这种规律的一般结论:
(2n+1)2-(2n-1)2=8n
3
7
11
11
6
例2
观察下列排列的等式:
1×2-1=12,
2×3-2=22,
3×4-3=32,
4×5-4=42,…….
猜想:第n个等式(n为正整数)
应为________________.
n(n+1)-n=n2
练一练
二、图形规律
例3 餐桌按下面的摆法可坐多少人
(2) 若按照上图的摆法摆放餐桌和椅子,完成下表:
(1) 1张餐桌可坐6人,2张餐桌可坐___人.
桌子张数 1 2 3 4 5 6 … n
可坐人数 6 10 …
10
14
18
4n+2
22
26
3.验证所归纳的结论。
回忆一下:
2.猜想规律与“序号n”间的对应关系。
关于寻找“图形序列”规律的思维步骤:
1.观察图形的排列规律找到基本图形,找到图形之间的变与不变的规律。
例4 联体长方形的摆法:(填空)
(1)如图,摆n个这样联体图形需 根火柴;
(2)如图,摆n个这样联体图形需 根火柴;
3n+1
5n+2
(3)如图,摆n个这样的联体图形需_______火柴;
(4)如图,摆n个这样联体图形需______根火柴.
7n+3
9n+4
练习
1.用红白两种颜色的正方形纸片,按红色纸片数逐一增加的规律拼成一列图案:
第一图
第二图
第三图
……
(1)第4个图案中,白色纸片一共有___张;
(2)第n个图案中,白色纸片一共有_____ 张;
3n+1
13
2.用黑白两种颜色的正方形纸片,按黑色纸片数逐一增加的规律拼成一列图案,第五个图案中,白色正方形的个数一共有_____个.
28
第一个
第二个
第三个
……
3.(湖南湘潭)为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:
按照上面的规律,摆个“金鱼”需用火柴棒的根数为( )
A.6n+2 B.6n+8
C.8n D.4n+4
A
4.如图所示,用火柴拼成一排由三角形组成的图形,如果要使图形中含有50个三角形,那么需要火柴( )
A.100根 B.101根
C.150根 D.153根
含有n个三角形需要( )根火柴
B
2n+1
5.如下图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n个小房子用了______________ 块石子.
(n+1)2+(2n-1)
(1)
(2)
(3)
(4)
3.验证所归纳的结论。
课堂小结
2.猜想规律与“序号”间的对应关系,用关于“序号”的数学式子表示出来。
一.关于寻找“数字序列”规律的思维步骤:
1.观察相邻数字间的数量关系,找到共同特征,得出某种规律的猜想。
3.验证所归纳的结论。
2.猜想规律与“序号”间的对应关系,用关于“序号”的数学式子表示出来。
二.关于寻找“图形序列”规律的思维步骤:
1.观察图形的排列规律找到基本图形,找到图形之间的变与不变的规律。
课堂小结
课堂小结
通过这节课的学习,你在思考问题的方法上,有哪些收获?
3n+2
14
课堂反馈
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
