沪科版数学七年级上册 4.5 角的比较与补(余)角课件(共20张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 4.5 角的比较与补(余)角课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 295.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 17:18:58 | ||
图片预览



文档简介
(共20张PPT)
角的比较与补(余)角
你还记得怎么样比较两条线段的长短吗?
1.度量法
2.叠合法
怎样比较两个角的大小呢?
?
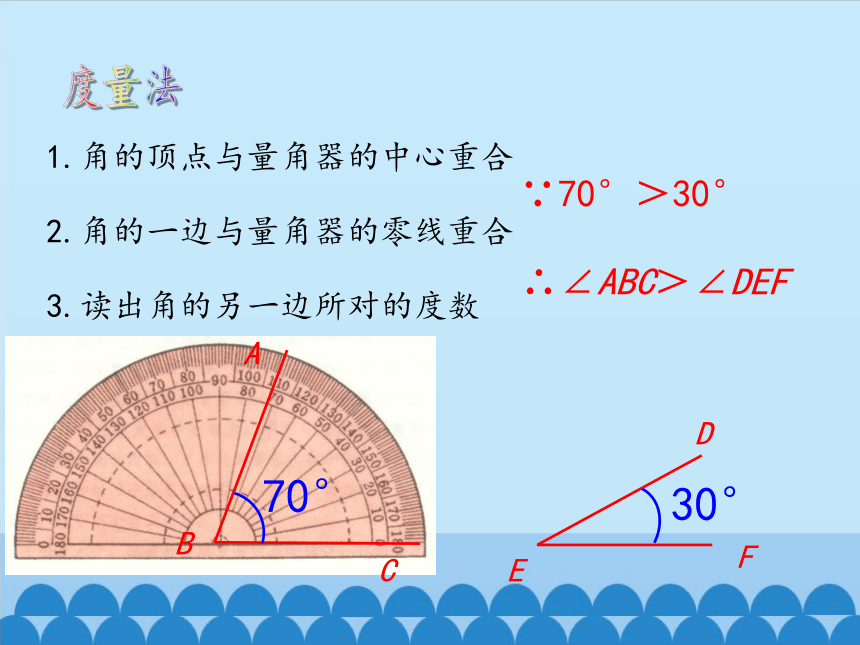
度量法
1.角的顶点与量角器的中心重合
2.角的一边与量角器的零线重合
3.读出角的另一边所对的度数
∵70°>30°
∴∠ABC>∠DEF
D
E
F
C
B
A
70°
30°
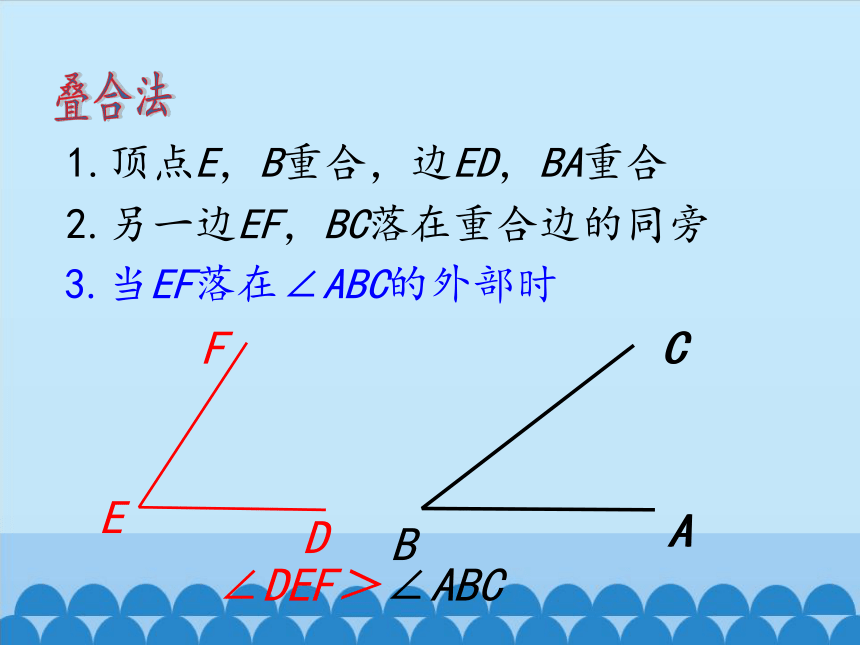
叠合法
1.顶点E,B重合,边ED,BA重合
2.另一边EF,BC落在重合边的同旁
3.当EF落在∠ABC的外部时
∠DEF>∠ABC
A
C
E
D
F
B
A
C
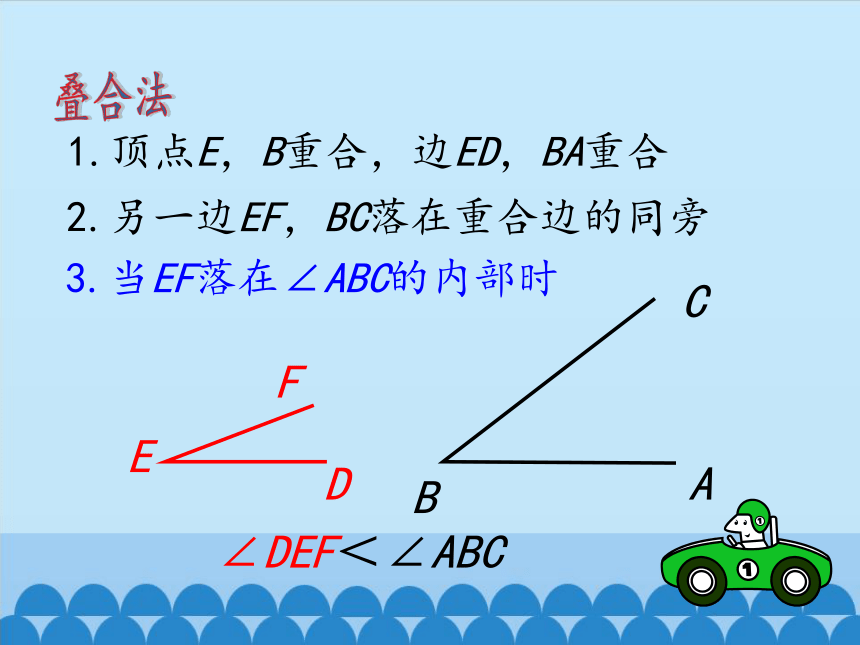
1.顶点E,B重合,边ED,BA重合
2.另一边EF,BC落在重合边的同旁
3.当EF落在∠ABC的内部时
∠DEF<∠ABC
B
A
C
F
D
E
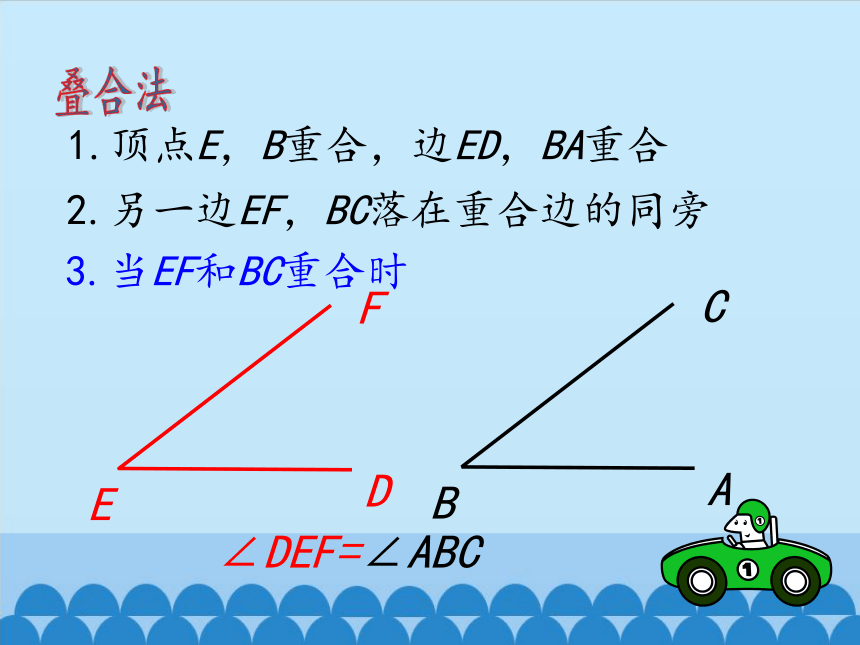
叠合法
1.顶点E,B重合,边ED,BA重合
2.另一边EF,BC落在重合边的同旁
3.当EF和BC重合时
∠DEF=∠ABC
E
D
F
B
A
C
叠合法
B
C
A
O
∠AOB,∠AOC,∠BOC之间有什么关系?
角的和差
∠AOC=∠AOB+∠BOC
∠AOB=∠AOC-∠BOC
∠BOC=∠AOC+∠AOB
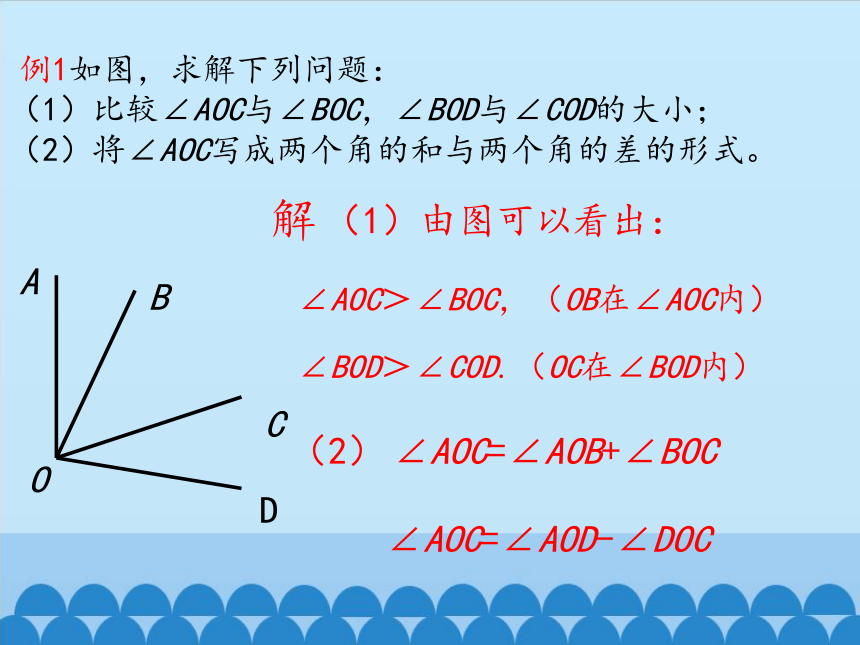
例1如图,求解下列问题:
(1)比较∠AOC与∠BOC,∠BOD与∠COD的大小;
(2)将∠AOC写成两个角的和与两个角的差的形式。
A
O
C
B
D
解
(1)由图可以看出:
∠AOC>∠BOC,(OB在∠AOC内)
∠BOD>∠COD.(OC在∠BOD内)
(2)
∠AOC=∠AOB+∠BOC
∠AOC=∠AOD-∠DOC
O
A
C
B
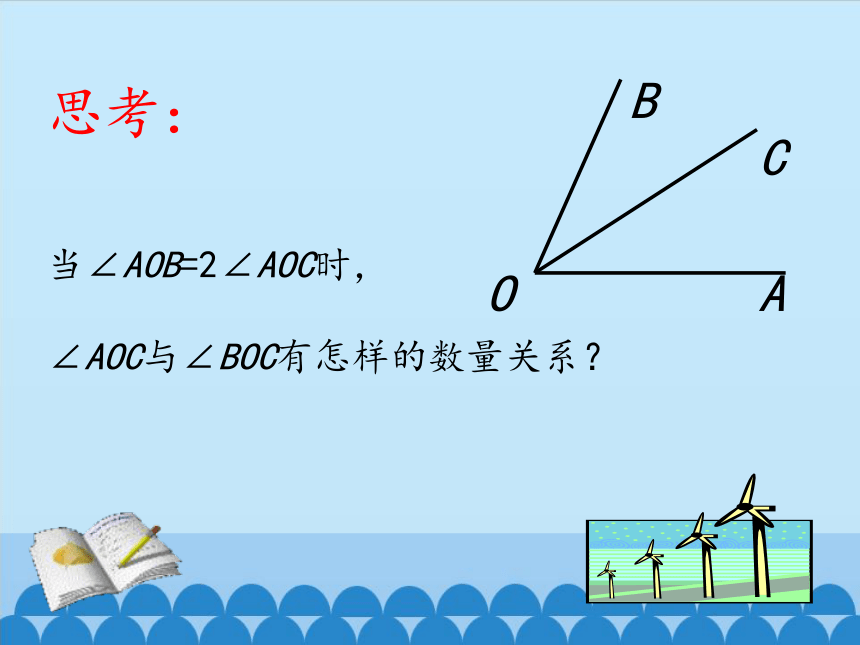
思考:
当∠AOB=2∠AOC时,
∠AOC与∠BOC有怎样的数量关系?
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线。
O
A
C
B
∵射线OC平分∠AOB
∴∠AOC=∠COB= ∠AOB
或∠AOB=2∠AOC=2∠BOC
想一想
如图,点A,O在同一条直线上,则∠AOC与∠BOC有怎样的关系?
∠AOC+∠BOC=180°
你还能举出一些具有这样关系的角吗?
若∠1=40°,∠2=140°,则∠1+∠2=180°
若∠α=65°,∠β=115°,则∠α+∠β=180°
……
C
A
O
B
如果两个角的和等于一个平角(180°),那么我们就称这两个角互为补角,简称互补。
1
2
平角
如图,
∠1+∠2=180°,
∠1叫做∠2的补角,
∠2也叫做∠1的补角,
∠1与∠2互补。
想一想
如图,∠AOB是直角,则∠AOC与∠BOC有怎样的关系?
O
C
B
A
∠AOC+∠BOC=90°
你还能举出一些具有这样关系的角吗?
若∠1=30°,∠2=60°,则∠1+∠2=90°
若∠α=25°,∠β=65°,则∠α+∠β=90°
……
如果两个角的和等于一个直角(90°),那么我们就称这两个角互为余角,简称互余。
α
β
直角
如图
∠α+∠β=90°,
∠α叫做∠β的余角,
∠β也叫做∠α的余角,
∠α与∠β互余。
(1)动手画一画:已知,如图,∠α,请利用三角板画∠α的补角。
图中∠α的补角∠1,∠2的大小有什么关系?为什么?
∵∠1=180°-∠α
∠2=180°-∠α
∴∠1=∠2
这一结论用文字怎么叙述?
同角的补角相等
α
1
2
图中∠α的补角为∠1,∠2。
∵∠1=180°-∠α
∠2=180°-∠β
∴∠1=∠2
这一结论用文字又怎么叙述?
等角的补角相等
如图,∠α=∠β,∠α的补角∠1,∠β的补角∠2的大小有什么关系?为什么?
β
α
2
1
又∵∠α=∠β
(1)动手画一画:已知,如图,∠α,请利用三角板画∠α的余角。
图中∠α的余角∠1,∠2的大小有什么关系?为什么?
∵∠1=90°-∠α
∠2=90°-∠α
∴∠1=∠2
这一结论用文字又怎么叙述?
同角的余角相等
α
1
2
图中∠α的余角为∠1,∠2。
∵∠1=90°-∠α
∠2=90°-∠β
∴∠1=∠2
这一结论用文字又怎么叙述?
等角的余角相等
如图,∠α=∠β,∠α的余角∠1,∠β的余角∠2的大小有什么关系?为什么?
β
α
2
1
又∵∠α=∠β
小结
1.角的大小比较方法
2.角的和差
3.三角板可拼出的角
4.角的平分线
5.补角和余角及其性质
谢 谢
角的比较与补(余)角
你还记得怎么样比较两条线段的长短吗?
1.度量法
2.叠合法
怎样比较两个角的大小呢?
?
度量法
1.角的顶点与量角器的中心重合
2.角的一边与量角器的零线重合
3.读出角的另一边所对的度数
∵70°>30°
∴∠ABC>∠DEF
D
E
F
C
B
A
70°
30°
叠合法
1.顶点E,B重合,边ED,BA重合
2.另一边EF,BC落在重合边的同旁
3.当EF落在∠ABC的外部时
∠DEF>∠ABC
A
C
E
D
F
B
A
C
1.顶点E,B重合,边ED,BA重合
2.另一边EF,BC落在重合边的同旁
3.当EF落在∠ABC的内部时
∠DEF<∠ABC
B
A
C
F
D
E
叠合法
1.顶点E,B重合,边ED,BA重合
2.另一边EF,BC落在重合边的同旁
3.当EF和BC重合时
∠DEF=∠ABC
E
D
F
B
A
C
叠合法
B
C
A
O
∠AOB,∠AOC,∠BOC之间有什么关系?
角的和差
∠AOC=∠AOB+∠BOC
∠AOB=∠AOC-∠BOC
∠BOC=∠AOC+∠AOB
例1如图,求解下列问题:
(1)比较∠AOC与∠BOC,∠BOD与∠COD的大小;
(2)将∠AOC写成两个角的和与两个角的差的形式。
A
O
C
B
D
解
(1)由图可以看出:
∠AOC>∠BOC,(OB在∠AOC内)
∠BOD>∠COD.(OC在∠BOD内)
(2)
∠AOC=∠AOB+∠BOC
∠AOC=∠AOD-∠DOC
O
A
C
B
思考:
当∠AOB=2∠AOC时,
∠AOC与∠BOC有怎样的数量关系?
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线。
O
A
C
B
∵射线OC平分∠AOB
∴∠AOC=∠COB= ∠AOB
或∠AOB=2∠AOC=2∠BOC
想一想
如图,点A,O在同一条直线上,则∠AOC与∠BOC有怎样的关系?
∠AOC+∠BOC=180°
你还能举出一些具有这样关系的角吗?
若∠1=40°,∠2=140°,则∠1+∠2=180°
若∠α=65°,∠β=115°,则∠α+∠β=180°
……
C
A
O
B
如果两个角的和等于一个平角(180°),那么我们就称这两个角互为补角,简称互补。
1
2
平角
如图,
∠1+∠2=180°,
∠1叫做∠2的补角,
∠2也叫做∠1的补角,
∠1与∠2互补。
想一想
如图,∠AOB是直角,则∠AOC与∠BOC有怎样的关系?
O
C
B
A
∠AOC+∠BOC=90°
你还能举出一些具有这样关系的角吗?
若∠1=30°,∠2=60°,则∠1+∠2=90°
若∠α=25°,∠β=65°,则∠α+∠β=90°
……
如果两个角的和等于一个直角(90°),那么我们就称这两个角互为余角,简称互余。
α
β
直角
如图
∠α+∠β=90°,
∠α叫做∠β的余角,
∠β也叫做∠α的余角,
∠α与∠β互余。
(1)动手画一画:已知,如图,∠α,请利用三角板画∠α的补角。
图中∠α的补角∠1,∠2的大小有什么关系?为什么?
∵∠1=180°-∠α
∠2=180°-∠α
∴∠1=∠2
这一结论用文字怎么叙述?
同角的补角相等
α
1
2
图中∠α的补角为∠1,∠2。
∵∠1=180°-∠α
∠2=180°-∠β
∴∠1=∠2
这一结论用文字又怎么叙述?
等角的补角相等
如图,∠α=∠β,∠α的补角∠1,∠β的补角∠2的大小有什么关系?为什么?
β
α
2
1
又∵∠α=∠β
(1)动手画一画:已知,如图,∠α,请利用三角板画∠α的余角。
图中∠α的余角∠1,∠2的大小有什么关系?为什么?
∵∠1=90°-∠α
∠2=90°-∠α
∴∠1=∠2
这一结论用文字又怎么叙述?
同角的余角相等
α
1
2
图中∠α的余角为∠1,∠2。
∵∠1=90°-∠α
∠2=90°-∠β
∴∠1=∠2
这一结论用文字又怎么叙述?
等角的余角相等
如图,∠α=∠β,∠α的余角∠1,∠β的余角∠2的大小有什么关系?为什么?
β
α
2
1
又∵∠α=∠β
小结
1.角的大小比较方法
2.角的和差
3.三角板可拼出的角
4.角的平分线
5.补角和余角及其性质
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
