沪科版数学七年级上册 3.2 一元一次方程的应用(3) 课件(共12张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.2 一元一次方程的应用(3) 课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 228.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 17:32:43 | ||
图片预览




文档简介
(共12张PPT)
3.2 一元一次方程的应用
1.解下列方程:
(1)
回顾旧知
(2)
3(2x-1)+2(5x+2)=4(3x-5).
解:去括号,得
6x-3+10x+4=12x-20
移项,得
6x+10x-12x=-20+3-4
合并同类项,得
4x=-21
系数化为1,得
X=
回顾旧知
2.圆柱的底面圆半径为r,高为h,则圆柱的体积V=__________.
3.长方体的长、宽、高分别为a,b,c,则其体积为V=________.
abc
Πr2h
请同学们思考:我们学习解方程的目的是什么?
我们学习解方程的目的是为了应用!
列方程解应用题
【例1 】
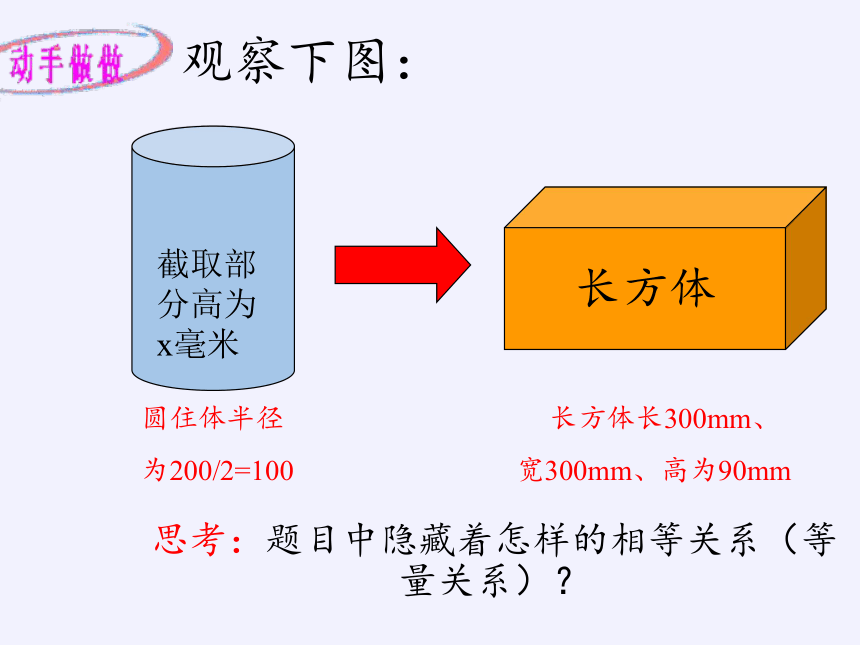
用直径为200mm的圆柱体钢,锻造一个长、宽、高分别是300mm、300mm和90mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
典型例析
思考:题目中隐藏着怎样的相等关系(等量关系)?
截取部分高为x毫米
长方体
观察下图:
圆住体半径 长方体长300mm、
为200/2=100 宽300mm、高为90mm
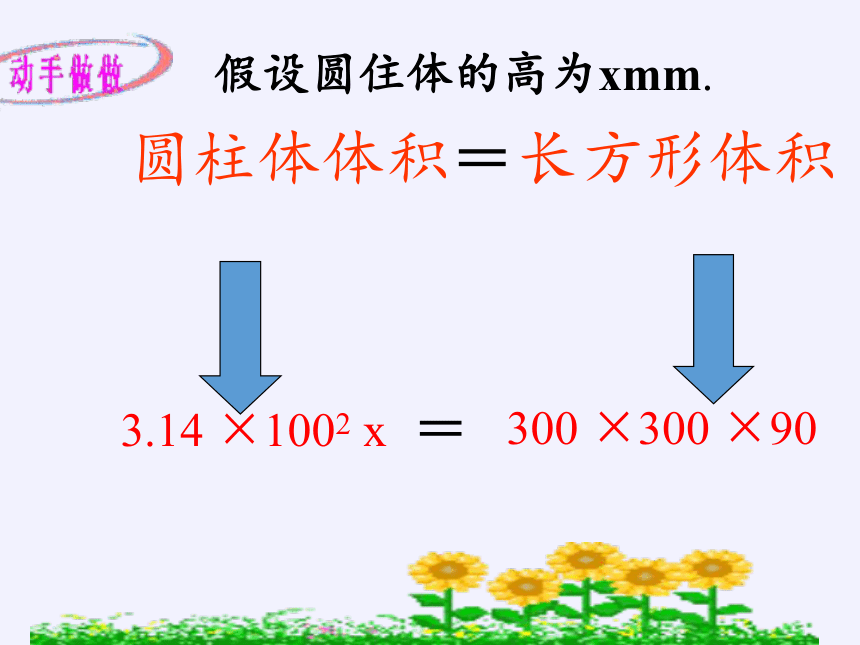
圆柱体体积=长方形体积
=
3.14 ×1002 x
300 ×300 ×90
假设圆住体的高为xmm.
解:设至少要截取圆柱体钢 mm.
根据题意得:
答:至少应截圆柱体钢长约是258mm
3.14 ×1002 =300 ×300 ×90
解得 ≈258
例2、 甲煤矿有煤432吨.乙煤矿有煤96吨,为了使甲煤矿存煤数是乙煤矿的2倍.应从甲煤矿运多少吨煤到乙煤矿?
分析:数量关系可用表来表示,看得更清楚,更直观.
原有煤量
调运煤量
调后存煤量
等量关系
煤 矿 甲 矿 乙 矿
432
96
- x
+ x
432 - x
96 + x
调后甲矿存煤量=2×调后乙矿存煤量
典型例析
解:设应从甲煤矿调运x吨煤到乙煤矿,那么调运后甲煤矿有煤(432- x )吨,
乙煤矿有煤(96 + x )吨,根据题意得:
432-x = 2(96+x)
得这个方程:432-x = 192+2x,
3x = 240
x = 80
答:应从甲煤矿调运80吨煤到乙煤矿.
1.将一个长、宽、高分别为6cm、2cm、47cm的长方体铁块和一个棱长为6cm的立方体铁块熔化成一个底面边长均为15cm的长方体,求这个长方体的高.
练
习
2. 一种小麦磨成面粉,出粉率为80%。为了得到
4500千克面粉,至少需要多少小麦?
3.甲、乙两车间共有120人,其中甲车间人数比乙车间
人数的4倍少5 人。求甲、乙两车间各有多少人.
要细心呦!
审设
找
列
解
检、答
感悟与反思
通过本节课学习,你能总结出列方程(组)解应用题的一般步骤吗?
1.弄清题意和题中的 ,用 表示问题中的 ;
2.分析题意;找出 关系;
3根据 关系列出所需的 ;
4.解 ;求出 ;
5. 检查 .
数量关系 字母
未知数
相等关系
相等 方程
方程 未知数的值
所得的值是否正确和符合实际情形
记住了
?
谢 谢
3.2 一元一次方程的应用
1.解下列方程:
(1)
回顾旧知
(2)
3(2x-1)+2(5x+2)=4(3x-5).
解:去括号,得
6x-3+10x+4=12x-20
移项,得
6x+10x-12x=-20+3-4
合并同类项,得
4x=-21
系数化为1,得
X=
回顾旧知
2.圆柱的底面圆半径为r,高为h,则圆柱的体积V=__________.
3.长方体的长、宽、高分别为a,b,c,则其体积为V=________.
abc
Πr2h
请同学们思考:我们学习解方程的目的是什么?
我们学习解方程的目的是为了应用!
列方程解应用题
【例1 】
用直径为200mm的圆柱体钢,锻造一个长、宽、高分别是300mm、300mm和90mm的长方体毛坯,应截取多少毫米长的圆柱体钢(计算时π取3.14,结果精确到1mm)?
典型例析
思考:题目中隐藏着怎样的相等关系(等量关系)?
截取部分高为x毫米
长方体
观察下图:
圆住体半径 长方体长300mm、
为200/2=100 宽300mm、高为90mm
圆柱体体积=长方形体积
=
3.14 ×1002 x
300 ×300 ×90
假设圆住体的高为xmm.
解:设至少要截取圆柱体钢 mm.
根据题意得:
答:至少应截圆柱体钢长约是258mm
3.14 ×1002 =300 ×300 ×90
解得 ≈258
例2、 甲煤矿有煤432吨.乙煤矿有煤96吨,为了使甲煤矿存煤数是乙煤矿的2倍.应从甲煤矿运多少吨煤到乙煤矿?
分析:数量关系可用表来表示,看得更清楚,更直观.
原有煤量
调运煤量
调后存煤量
等量关系
煤 矿 甲 矿 乙 矿
432
96
- x
+ x
432 - x
96 + x
调后甲矿存煤量=2×调后乙矿存煤量
典型例析
解:设应从甲煤矿调运x吨煤到乙煤矿,那么调运后甲煤矿有煤(432- x )吨,
乙煤矿有煤(96 + x )吨,根据题意得:
432-x = 2(96+x)
得这个方程:432-x = 192+2x,
3x = 240
x = 80
答:应从甲煤矿调运80吨煤到乙煤矿.
1.将一个长、宽、高分别为6cm、2cm、47cm的长方体铁块和一个棱长为6cm的立方体铁块熔化成一个底面边长均为15cm的长方体,求这个长方体的高.
练
习
2. 一种小麦磨成面粉,出粉率为80%。为了得到
4500千克面粉,至少需要多少小麦?
3.甲、乙两车间共有120人,其中甲车间人数比乙车间
人数的4倍少5 人。求甲、乙两车间各有多少人.
要细心呦!
审设
找
列
解
检、答
感悟与反思
通过本节课学习,你能总结出列方程(组)解应用题的一般步骤吗?
1.弄清题意和题中的 ,用 表示问题中的 ;
2.分析题意;找出 关系;
3根据 关系列出所需的 ;
4.解 ;求出 ;
5. 检查 .
数量关系 字母
未知数
相等关系
相等 方程
方程 未知数的值
所得的值是否正确和符合实际情形
记住了
?
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
