沪科版数学七年级上册 3.4 二元一次方程组的应用 (2) 课件(共33张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.4 二元一次方程组的应用 (2) 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 860.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 17:34:31 | ||
图片预览











文档简介
(共33张PPT)
二元一次方程组的应用
路上偶遇小学生四明山春游,同学们坐在凳子上等导游。一个戴帽子的同学说,我看见戴帽子的同学人数是不戴帽子的同学人数的7倍;一个不戴帽子的同学说,我看见戴帽子的同学人数是不戴帽子的同学人数的11倍.你知道戴帽子的同学和不戴帽子的同学各有多少人吗?
路上偶遇小学生四明山春游。同学们坐在凳子上等导游。一个戴帽子的同学说,我看见戴帽子的同学人数是不戴帽子的同学人数的7倍;一个不戴帽子的同学说,我看见戴帽子的同学人数是不戴帽子的同学人数的11倍.你知道戴帽子的同学和不戴帽子的同学各有多少人吗?
老师的问题:
本题能列一元一次方程吗?
能.
用列二元一次方程组的方法求解应用题:
当问题中所求的未知数有两个时,
用两个字母来表示未知数往往能使问题变得简单,比较容易找出等量关系,列出方程.
归纳
要注意的是必须寻找两个等量关系,列出两个不同的方程,组成二元一次方程组.
小王和小李边挖笋边聊天,小王说:我挖的笋是你的2倍,小李一听,从小王那里拿来4株笋 ,说:这样我们的笋一样多.问小李和小王各自挖了多少株笋?
想一想: 应用二元一次方程组解决实际问题的过程中,你经历了哪些问题解决的基本步骤
竹海山林享笋趣
应用二元一次方程组解决实际问题
的基本步骤:
剥笋式解题
3.执行计划
1.理解问题
2.制订计划
4.回顾
(审题,搞清已知和未知,分析数量关系)
(考虑如何根据等量关系设元,列出方程组)
(列出方程组并求解,得到答案)
(检查和反思解题过程,检验答案的正确性以及是否符合题意)
加减消元法
二元一次方程组的解法
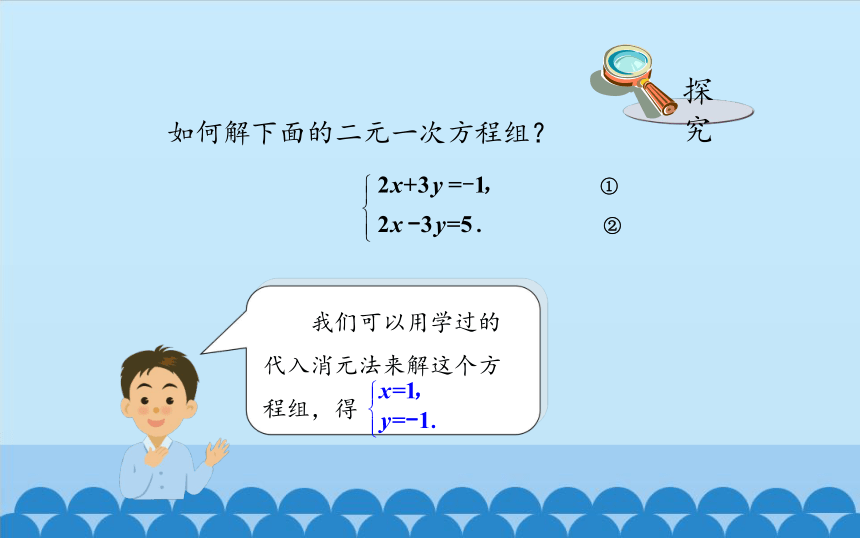
如何解下面的二元一次方程组?
探究
我们可以用学过的代入消元法来解这个方程组,得
还有没有更简单的解法呢?
我们知道解二元一次方程组的关键是消去一个未知数,使方程组转化为一个一元一次方程。
分析方程①和②,可以发现未知数x的系数相同,因此只要把这两个方程的两边分别相减,就可以消去其中一个未知数x,得到一个一元一次方程。
2x+3y=-1
(2x-3y=5)
6y=-6
-
即①-②,得2x+3y-(2x-3y)=-1-5
6y=-6,
解得y=-1,
把y=-1代入①式,得2x+3×(-1)=-1,
解得x=1,
因此原方程组的解是
把y=-1代入②式可以吗?
解上述方程组时,在消元的过程中,如果把方程①与方程②相加,可以消去一个未知数吗?
做一做
例3:解二元一次方程组:
举
例
代入消元法
二元一次方程组的解法
我们列出了二元一次方程组:
探究
知道x=40,y=20是这个方程组的一个解。那么,这个解是怎么得到呢?
我会解一元一次方程,可是现在方程①和②中都有两个未知数……
方程①和②中的x都表示1月份的天然气费,y都表示1月份的水费,因此方程②中的x,y分别与方程①中的x,y的值相同。
由②式可得x=y+20, ③
于是可以把③代入①式,得(y+20)+y=60, ④
解方程④,得y = 。
把y的值代入③式, 得x= 。
因此原方程组的解是
20
40
40
20
议一议
同桌同学讨论,解二元一次方程组的基本想法是什么?
例1:解二元一次方程组:
举
例
解:由②式得
y=-3x+1, ③
把③代入①式,
因此原方程组的解是
可以把求得的x,y的值代入原方程组检验,看是否为方程组的解。
把x=-1代入③式,得y=4,
解得x=-1,
得5x-(-3x+1)=-9,
结论
解二元一次方程组的基本想法是:消去一个未知数(简称为消元),得到一个一元一次方程,然后解这个一元一次方程。
在上面的例子中,消去一个未知数的方法是:把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程。
这种解方程组的方法叫做代入消元法,简称为代入法。
例2:用代入法解方程组:
举
例
把y=2代入③式,得x=3,
因此原方程组的解是
解:由①式得
把③代入②式,得
解得y=2,
在例2中,用含x的代数式表示y来解原方程组。
做一做
练习
1.把下列方程改写为用含x的代数式表示y的形式。
(1)2x-y=-1;(2)x+2y-2=0 。
答:(1)y=2x+1;(2) 。
2.用代入法解下列二元一次方程组:
解:从②得x=4+y, ③
把③代入①,得
(4+y)+y=128
y=62
把y=62代入③,得x=66,
因此原方程组的一个解是
解:把②代入①,得
3x+2(2x-1)=5, ③
解得x=1,
把x=1代入②,得y=1,
因此原方程组的一个解是
解:从②得b=7-3a, ③
5a+2(7-3a)=11
把③代入①,得
把a=3代入③,得
a=3
b=-2,
因此原方程组的一个解是
解:从①得n=3m+1, ③
把③代入②,得
2m+3(3m+1)-3=0
m=0
把m=0代入③,得
n=1,
因此原方程组的一个解是
中考 试题
方程组 的解是 。
由②得x=2-2y, ③
解析
把③代入①,得y=1,
把y=1代入②得x=0,
∴原方程组的解为
例1:
方程组 的解是 。
将①代入②得x=1,
解析
例2:
把x=1代入①得y=2,
所以原方程组的解为
谢谢大家
二元一次方程组的应用
路上偶遇小学生四明山春游,同学们坐在凳子上等导游。一个戴帽子的同学说,我看见戴帽子的同学人数是不戴帽子的同学人数的7倍;一个不戴帽子的同学说,我看见戴帽子的同学人数是不戴帽子的同学人数的11倍.你知道戴帽子的同学和不戴帽子的同学各有多少人吗?
路上偶遇小学生四明山春游。同学们坐在凳子上等导游。一个戴帽子的同学说,我看见戴帽子的同学人数是不戴帽子的同学人数的7倍;一个不戴帽子的同学说,我看见戴帽子的同学人数是不戴帽子的同学人数的11倍.你知道戴帽子的同学和不戴帽子的同学各有多少人吗?
老师的问题:
本题能列一元一次方程吗?
能.
用列二元一次方程组的方法求解应用题:
当问题中所求的未知数有两个时,
用两个字母来表示未知数往往能使问题变得简单,比较容易找出等量关系,列出方程.
归纳
要注意的是必须寻找两个等量关系,列出两个不同的方程,组成二元一次方程组.
小王和小李边挖笋边聊天,小王说:我挖的笋是你的2倍,小李一听,从小王那里拿来4株笋 ,说:这样我们的笋一样多.问小李和小王各自挖了多少株笋?
想一想: 应用二元一次方程组解决实际问题的过程中,你经历了哪些问题解决的基本步骤
竹海山林享笋趣
应用二元一次方程组解决实际问题
的基本步骤:
剥笋式解题
3.执行计划
1.理解问题
2.制订计划
4.回顾
(审题,搞清已知和未知,分析数量关系)
(考虑如何根据等量关系设元,列出方程组)
(列出方程组并求解,得到答案)
(检查和反思解题过程,检验答案的正确性以及是否符合题意)
加减消元法
二元一次方程组的解法
如何解下面的二元一次方程组?
探究
我们可以用学过的代入消元法来解这个方程组,得
还有没有更简单的解法呢?
我们知道解二元一次方程组的关键是消去一个未知数,使方程组转化为一个一元一次方程。
分析方程①和②,可以发现未知数x的系数相同,因此只要把这两个方程的两边分别相减,就可以消去其中一个未知数x,得到一个一元一次方程。
2x+3y=-1
(2x-3y=5)
6y=-6
-
即①-②,得2x+3y-(2x-3y)=-1-5
6y=-6,
解得y=-1,
把y=-1代入①式,得2x+3×(-1)=-1,
解得x=1,
因此原方程组的解是
把y=-1代入②式可以吗?
解上述方程组时,在消元的过程中,如果把方程①与方程②相加,可以消去一个未知数吗?
做一做
例3:解二元一次方程组:
举
例
代入消元法
二元一次方程组的解法
我们列出了二元一次方程组:
探究
知道x=40,y=20是这个方程组的一个解。那么,这个解是怎么得到呢?
我会解一元一次方程,可是现在方程①和②中都有两个未知数……
方程①和②中的x都表示1月份的天然气费,y都表示1月份的水费,因此方程②中的x,y分别与方程①中的x,y的值相同。
由②式可得x=y+20, ③
于是可以把③代入①式,得(y+20)+y=60, ④
解方程④,得y = 。
把y的值代入③式, 得x= 。
因此原方程组的解是
20
40
40
20
议一议
同桌同学讨论,解二元一次方程组的基本想法是什么?
例1:解二元一次方程组:
举
例
解:由②式得
y=-3x+1, ③
把③代入①式,
因此原方程组的解是
可以把求得的x,y的值代入原方程组检验,看是否为方程组的解。
把x=-1代入③式,得y=4,
解得x=-1,
得5x-(-3x+1)=-9,
结论
解二元一次方程组的基本想法是:消去一个未知数(简称为消元),得到一个一元一次方程,然后解这个一元一次方程。
在上面的例子中,消去一个未知数的方法是:把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程。
这种解方程组的方法叫做代入消元法,简称为代入法。
例2:用代入法解方程组:
举
例
把y=2代入③式,得x=3,
因此原方程组的解是
解:由①式得
把③代入②式,得
解得y=2,
在例2中,用含x的代数式表示y来解原方程组。
做一做
练习
1.把下列方程改写为用含x的代数式表示y的形式。
(1)2x-y=-1;(2)x+2y-2=0 。
答:(1)y=2x+1;(2) 。
2.用代入法解下列二元一次方程组:
解:从②得x=4+y, ③
把③代入①,得
(4+y)+y=128
y=62
把y=62代入③,得x=66,
因此原方程组的一个解是
解:把②代入①,得
3x+2(2x-1)=5, ③
解得x=1,
把x=1代入②,得y=1,
因此原方程组的一个解是
解:从②得b=7-3a, ③
5a+2(7-3a)=11
把③代入①,得
把a=3代入③,得
a=3
b=-2,
因此原方程组的一个解是
解:从①得n=3m+1, ③
把③代入②,得
2m+3(3m+1)-3=0
m=0
把m=0代入③,得
n=1,
因此原方程组的一个解是
中考 试题
方程组 的解是 。
由②得x=2-2y, ③
解析
把③代入①,得y=1,
把y=1代入②得x=0,
∴原方程组的解为
例1:
方程组 的解是 。
将①代入②得x=1,
解析
例2:
把x=1代入①得y=2,
所以原方程组的解为
谢谢大家
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
