鲁教版(五四制)数学七年级上册 第二章 轴对称 复习(课件)(共39张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 第二章 轴对称 复习(课件)(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 18:22:18 | ||
图片预览









文档简介
(共39张PPT)
第二章 轴对称
复习课件
一、轴对称中的相关概念
1.轴对称与轴对称图形
(1)轴对称图形:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
(2)轴对称:对于两个图形,如果沿一条直线对折后,它们能完全重合,那么称这两个图形关于这条直线成轴对称,这条直线就是对称轴。
2.线段的垂直平分线
线段是轴对称图形,它的一条对称轴垂直于这条线段并且平分它,这样的直线叫做这条线段的垂直平分线(简称中垂线)。
二、轴对称的相关性质与判定
1.轴对称的性质
(1)对应点所连的线段被对称轴垂直平分。
(2)对应线段相等、对应角相等。
名称 关系 轴对称 轴对称图形
区 别 图形个数 两个 一个
实质 两个图形的位置和数量关系 一个特殊图形
联系 (1)定义中都有一条直线,都要沿着这条直线折叠重合。(2)如果把轴对称图形沿对称轴分成两部分(即看成两个图形),那么这两个图形就关于这条直线成轴对称;反过来,如果把轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。
【知识辨析】
二者的区别与联系
2.角平分线的性质:角平分线上的点到这个角两边的距离相等.
3.线段垂直平分线的性质:线段的垂直平分线上的点到这条线段两端点的距离相等.
4.等腰三角形、等边三角形的性质和判定.
名称 项目 等腰三角形 等边三角形
性 质 ①边:两腰相等; ②角:两个底角相等(等边对等角); ③重要线段:顶角的平分线、底边的中线、底边上的高互相重合(三线合一); ④对称性:是轴对称图形,对称轴为顶角的平分线或底边的中线或底边上的高所在的直线 ①边:三边都相等;
②角:三个角都相等,都等于60°;
③重要线段:与等腰三角形的相同;
④对称性:是轴对称图形,对称轴有三条
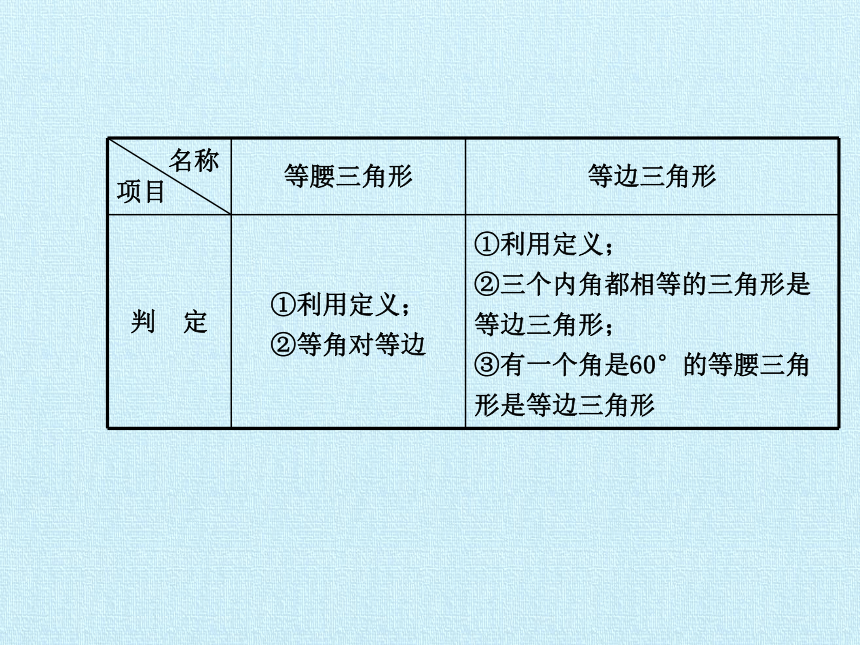
名称 项目 等腰三角形 等边三角形
判 定 ①利用定义; ②等角对等边 ①利用定义;
②三个内角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形
三、轴对称的相关应用
1.等腰三角形
等腰三角形的性质和判定是证明两个角和两条线段相等的重要依据,当证明同一个三角形中的两个角或两条线段相等时,经常利用等腰三角形的性质定理或判定定理.
当然,全等三角形的性质也是证明两个角和两条线段相等的重要依据,它们的区别主要是看待证的两个角和两条线段是否位于同一个三角形中.
2.轴对称作图
(1)作一个点A关于直线l的对称点A′.
作法:过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
(2)作一个△ABC关于直线l成轴对称的图形△A′B′C′.
作法:①过点A作直线l的垂线,垂足为O,
在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
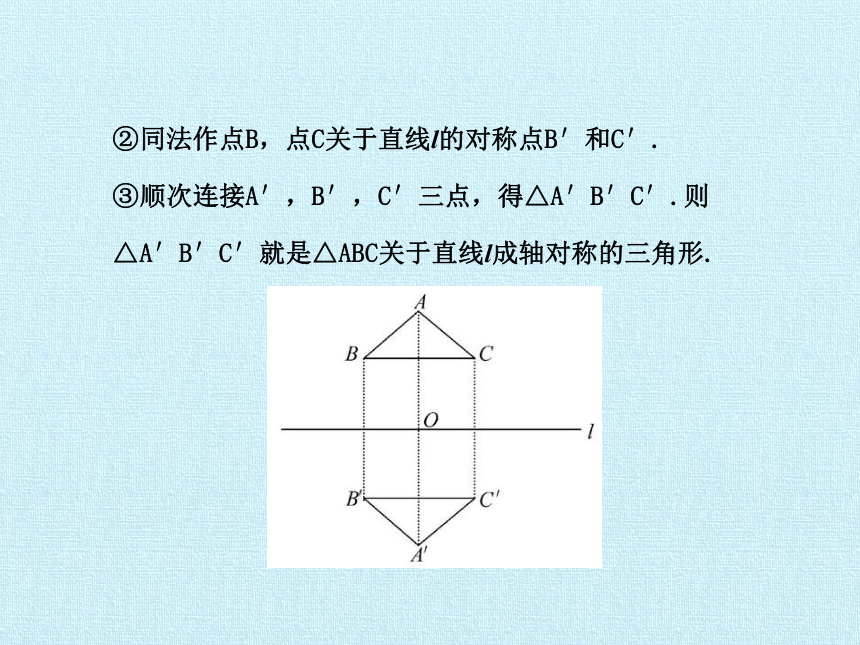
②同法作点B,点C关于直线l的对称点B′和C′.
③顺次连接A′,B′,C′三点,得△A′B′C′.则△A′B′C′就是△ABC关于直线l成轴对称的三角形.
热点考向1轴对称与轴对称图形
【相关链接】
(1)轴对称是对两个图形来说的,它是一种图形变换,该变换不改变图形的形状和大小,仅改变图形的位置.
(2)轴对称图形是对一个图形来说的,识别轴对称图形的关键是找其对称轴,看是否存在直线,沿这条直线折叠,折痕两旁的部分能完全重合.
【例1】(2012·连云港中考)下列图案是轴对称图形的是( )
【思路点拨】轴对称定义→判断→结论
【自主解答】选D.把D选项沿一直线折叠,直线两侧部分能重合,故D选项是轴对称图形.其余图形均不能找到一条直线,使图形沿该直线折叠,直线两侧的部分能完全重合,所以不是轴对称图形.
热点考向2 线段垂直平分线的性质及其应用
【相关链接】
线段垂直平分线的性质和判定在几何的推理和证明中应用广泛,利用尺规作出线段的垂直平分线,在规划、设计和实际生活中也有重要应用.例如作直线的垂线,找线段的中点等,因此,学习数学,要学会用学到的知识去解决生活中的问题.
【例2】(2012·德州中考)有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置(保留作图痕迹,不要求写出画法).
【思路点拨】利用线段垂直平分线及角平分线的性质解题.
【自主解答】根据题意知道,点C应满足两个条件,一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是它们的交点.
(1)作两条公路夹角的平分线OD或OE.
(2)作线段AB的垂直平分线FG.则射线OD,OE与直线FG的交点C1,C2就是所求的位置.
如图所示:
热点考向3 等腰三角形的性质与判定应用
【相关链接】
等腰三角形包括等边三角形,它们的性质和判定应用非常广泛,其中“三线合一”的性质非常重要;“等边对等角”“等角对等边”把边与角有机地联系在一起,为角的计算,三角形全等的说明提供了条件.
【例3】(2012·河源中考改编)如图,已知
AB=CD,∠B=∠C,AC和BD相交于点O,E是AD
的中点,连接OE.
(1)试说明△AOB≌△DOC.
(2)求∠AEO的度数.
【教你解题】(1)
(2)
【命题揭秘】
结合近几年中考试题分析,对轴对称图形内容的考查主要有以下特点:
1.考查的内容为轴对称的性质、相关的图案设计、与图形轴对称相关的计算等;题型较全,一般有选择题、填空题和解答题,有时以探索研究题型出现,多属中、低档题.
2.命题内容为对等腰三角形的性质、角平分线的性质、线段垂直平分线性质等的考查,也常以综合题的形式进行考查.
1.(2011·达州中考)图中所示的几个图形是国际通用的交通标志.其中不是轴对称图形的是( )
【解析】选C.只有C不能找到对称轴.
2.如图,把一张长方形ABCD的纸片,沿EF折叠后,ED与BC交于点G,点D,点C分别落在D′,C′位置上,若∠EFG=52°,则∠BGE=( )
(A)92° (B)100° (C)104° (D)76°
【解析】选C.因为纸片是长方形,所以AD∥BC,
所以∠DEF=∠EFG.
又因为∠EFG=52°,
所以∠DEF=52°,
根据轴对称的性质,∠GEF=∠DEF=52°,
所以∠BGE=∠GED=52°+52°=104°.
3.(2012·河池中考)如图,在△ABC中,
∠B=30°,BC的垂直平分线交AB于E,
垂足为D,若ED=5,则CE的长为( )
(A)10 (B)8 (C)5 (D)2.5
【解析】选A.因为ED垂直平分BC,所以EB=EC,
在Rt△BDE中,因为∠B=30°,所以EB=2ED=2×5=10,所以CE=10.
4.已知等腰三角形的一个内角为70°,则另两个内角的度数
是( )
(A)55°,55° (B)70°,40°
(C)55°,55°或70°,40° (D)以上都不对
【解析】选C.当70°的角是顶角时,另两个内角都是(180°-70°)÷2=55°.当70°的角是底角时,则另两个角中的底角是70°,顶角是180°-70°-70°=40°.因此选C.
5.如图所示,已知Rt△ABC中,∠C=90°,
沿过B点的一条直线BE折叠这个三角形,
使C点落在AB边上的点D处,要使点D恰
为AB的中点,问在图中还要添加什么条件?
(直接填写答案)
(1)写出一条边满足的条件:______________.
(2)写出一个角满足的条件:______________.
(3)写出一个除边、角以外的其他满足条件:___________.
【解析】(1) AB=BC.
理由:由轴对称的性质可得:BC=BD,又因为BC= AB=BD.所以可得D在AB的中点位置.
(2)∠A=30°.
理由:由轴对称的性质得:BC=BD,CE=DE,∠CBE=∠DBE=∠A=30°.
所以可得:△ADE≌△BCE,AD=BC=BD.即得:点D在AB的中点。
(3)△BEC≌△AED.
理由:因为△BEC≌△AED.所以AD=BC,又BC=BD,所以AD=BD,故点D为AB的中点.
答案:(1)AB=BC (2)∠A=30°
(3)△BEC≌△AED
6.如图所示,一牧童在A处放牛,其家在B处,
A,B到河岸的距离分别为AC,BD,且AC=BD.
若A到河岸CD的中点距离为500米,问:
(1)牧童从A处把牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?
(2)最短路程是多少?
【解析】(1)如图所示,①作点A关于直
线CD的对称点A1.②连接A1B交CD于M,则在M处饮水所走路
程最短.
(2)由(1)知:A1C=AC=BD,∠A1CM=∠BDM,∠A1MC=∠BMD,故△A1CM≌△BDM.所以A1M=BM,CM=DM,所以M为CD的中点,AM=500米,
所以A1B=2×500=1000(米).故最短路程为1000米.
7.(2012·随州中考)如图,在△ABC中,
AB=AC,点D是BC的中点,点E在AD上.
试说明(1)△ABD≌△ACD.
(2)BE=CE.
【解析】(1)在△ABD和△ACD中,
因为D是BC的中点,所以BD=CD,因为AB=AC,AD=AD,所以△ABD≌△ACD(SSS).
(2)由(1)知△ABD≌△ACD,所以∠BAD=∠CAD,即∠BAE=∠CAE,
在△ABE和△ACE中,
所以BE=CE.
8.如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
(1)写出点D到△ABC的三个顶点
A,B,C的距离关系(不要求说明).
(2)如果点M,N分别在线段AB,AC上移动,
在移动中保持AN=BM,请判断△DMN的形状,并说明你的结论.
【解析】(1)DA=DB=DC.
(2)△DMN为等腰直角三角形.
说明:连接AD,因为AB=AC,∠BAC=90°,所以∠B=45°.
又因为D为BC的中点,所以AD平分∠CAB,所以AD⊥BC,∠CAD=45°.
在△ADN和△BDM中,
所以△ADN≌△BDM(SAS),
所以DM=DN,∠NDA=∠BDM.
因为AD⊥BC,所以∠ADB=90°.
因为∠ADB=∠ADM+∠BDM,
所以∠MDN=∠ADM+∠ADN
=∠ADM+∠BDM=90°,
所以△DMN是等腰直角三角形.
谢 谢
第二章 轴对称
复习课件
一、轴对称中的相关概念
1.轴对称与轴对称图形
(1)轴对称图形:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
(2)轴对称:对于两个图形,如果沿一条直线对折后,它们能完全重合,那么称这两个图形关于这条直线成轴对称,这条直线就是对称轴。
2.线段的垂直平分线
线段是轴对称图形,它的一条对称轴垂直于这条线段并且平分它,这样的直线叫做这条线段的垂直平分线(简称中垂线)。
二、轴对称的相关性质与判定
1.轴对称的性质
(1)对应点所连的线段被对称轴垂直平分。
(2)对应线段相等、对应角相等。
名称 关系 轴对称 轴对称图形
区 别 图形个数 两个 一个
实质 两个图形的位置和数量关系 一个特殊图形
联系 (1)定义中都有一条直线,都要沿着这条直线折叠重合。(2)如果把轴对称图形沿对称轴分成两部分(即看成两个图形),那么这两个图形就关于这条直线成轴对称;反过来,如果把轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。
【知识辨析】
二者的区别与联系
2.角平分线的性质:角平分线上的点到这个角两边的距离相等.
3.线段垂直平分线的性质:线段的垂直平分线上的点到这条线段两端点的距离相等.
4.等腰三角形、等边三角形的性质和判定.
名称 项目 等腰三角形 等边三角形
性 质 ①边:两腰相等; ②角:两个底角相等(等边对等角); ③重要线段:顶角的平分线、底边的中线、底边上的高互相重合(三线合一); ④对称性:是轴对称图形,对称轴为顶角的平分线或底边的中线或底边上的高所在的直线 ①边:三边都相等;
②角:三个角都相等,都等于60°;
③重要线段:与等腰三角形的相同;
④对称性:是轴对称图形,对称轴有三条
名称 项目 等腰三角形 等边三角形
判 定 ①利用定义; ②等角对等边 ①利用定义;
②三个内角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形
三、轴对称的相关应用
1.等腰三角形
等腰三角形的性质和判定是证明两个角和两条线段相等的重要依据,当证明同一个三角形中的两个角或两条线段相等时,经常利用等腰三角形的性质定理或判定定理.
当然,全等三角形的性质也是证明两个角和两条线段相等的重要依据,它们的区别主要是看待证的两个角和两条线段是否位于同一个三角形中.
2.轴对称作图
(1)作一个点A关于直线l的对称点A′.
作法:过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
(2)作一个△ABC关于直线l成轴对称的图形△A′B′C′.
作法:①过点A作直线l的垂线,垂足为O,
在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
②同法作点B,点C关于直线l的对称点B′和C′.
③顺次连接A′,B′,C′三点,得△A′B′C′.则△A′B′C′就是△ABC关于直线l成轴对称的三角形.
热点考向1轴对称与轴对称图形
【相关链接】
(1)轴对称是对两个图形来说的,它是一种图形变换,该变换不改变图形的形状和大小,仅改变图形的位置.
(2)轴对称图形是对一个图形来说的,识别轴对称图形的关键是找其对称轴,看是否存在直线,沿这条直线折叠,折痕两旁的部分能完全重合.
【例1】(2012·连云港中考)下列图案是轴对称图形的是( )
【思路点拨】轴对称定义→判断→结论
【自主解答】选D.把D选项沿一直线折叠,直线两侧部分能重合,故D选项是轴对称图形.其余图形均不能找到一条直线,使图形沿该直线折叠,直线两侧的部分能完全重合,所以不是轴对称图形.
热点考向2 线段垂直平分线的性质及其应用
【相关链接】
线段垂直平分线的性质和判定在几何的推理和证明中应用广泛,利用尺规作出线段的垂直平分线,在规划、设计和实际生活中也有重要应用.例如作直线的垂线,找线段的中点等,因此,学习数学,要学会用学到的知识去解决生活中的问题.
【例2】(2012·德州中考)有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置(保留作图痕迹,不要求写出画法).
【思路点拨】利用线段垂直平分线及角平分线的性质解题.
【自主解答】根据题意知道,点C应满足两个条件,一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是它们的交点.
(1)作两条公路夹角的平分线OD或OE.
(2)作线段AB的垂直平分线FG.则射线OD,OE与直线FG的交点C1,C2就是所求的位置.
如图所示:
热点考向3 等腰三角形的性质与判定应用
【相关链接】
等腰三角形包括等边三角形,它们的性质和判定应用非常广泛,其中“三线合一”的性质非常重要;“等边对等角”“等角对等边”把边与角有机地联系在一起,为角的计算,三角形全等的说明提供了条件.
【例3】(2012·河源中考改编)如图,已知
AB=CD,∠B=∠C,AC和BD相交于点O,E是AD
的中点,连接OE.
(1)试说明△AOB≌△DOC.
(2)求∠AEO的度数.
【教你解题】(1)
(2)
【命题揭秘】
结合近几年中考试题分析,对轴对称图形内容的考查主要有以下特点:
1.考查的内容为轴对称的性质、相关的图案设计、与图形轴对称相关的计算等;题型较全,一般有选择题、填空题和解答题,有时以探索研究题型出现,多属中、低档题.
2.命题内容为对等腰三角形的性质、角平分线的性质、线段垂直平分线性质等的考查,也常以综合题的形式进行考查.
1.(2011·达州中考)图中所示的几个图形是国际通用的交通标志.其中不是轴对称图形的是( )
【解析】选C.只有C不能找到对称轴.
2.如图,把一张长方形ABCD的纸片,沿EF折叠后,ED与BC交于点G,点D,点C分别落在D′,C′位置上,若∠EFG=52°,则∠BGE=( )
(A)92° (B)100° (C)104° (D)76°
【解析】选C.因为纸片是长方形,所以AD∥BC,
所以∠DEF=∠EFG.
又因为∠EFG=52°,
所以∠DEF=52°,
根据轴对称的性质,∠GEF=∠DEF=52°,
所以∠BGE=∠GED=52°+52°=104°.
3.(2012·河池中考)如图,在△ABC中,
∠B=30°,BC的垂直平分线交AB于E,
垂足为D,若ED=5,则CE的长为( )
(A)10 (B)8 (C)5 (D)2.5
【解析】选A.因为ED垂直平分BC,所以EB=EC,
在Rt△BDE中,因为∠B=30°,所以EB=2ED=2×5=10,所以CE=10.
4.已知等腰三角形的一个内角为70°,则另两个内角的度数
是( )
(A)55°,55° (B)70°,40°
(C)55°,55°或70°,40° (D)以上都不对
【解析】选C.当70°的角是顶角时,另两个内角都是(180°-70°)÷2=55°.当70°的角是底角时,则另两个角中的底角是70°,顶角是180°-70°-70°=40°.因此选C.
5.如图所示,已知Rt△ABC中,∠C=90°,
沿过B点的一条直线BE折叠这个三角形,
使C点落在AB边上的点D处,要使点D恰
为AB的中点,问在图中还要添加什么条件?
(直接填写答案)
(1)写出一条边满足的条件:______________.
(2)写出一个角满足的条件:______________.
(3)写出一个除边、角以外的其他满足条件:___________.
【解析】(1) AB=BC.
理由:由轴对称的性质可得:BC=BD,又因为BC= AB=BD.所以可得D在AB的中点位置.
(2)∠A=30°.
理由:由轴对称的性质得:BC=BD,CE=DE,∠CBE=∠DBE=∠A=30°.
所以可得:△ADE≌△BCE,AD=BC=BD.即得:点D在AB的中点。
(3)△BEC≌△AED.
理由:因为△BEC≌△AED.所以AD=BC,又BC=BD,所以AD=BD,故点D为AB的中点.
答案:(1)AB=BC (2)∠A=30°
(3)△BEC≌△AED
6.如图所示,一牧童在A处放牛,其家在B处,
A,B到河岸的距离分别为AC,BD,且AC=BD.
若A到河岸CD的中点距离为500米,问:
(1)牧童从A处把牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?
(2)最短路程是多少?
【解析】(1)如图所示,①作点A关于直
线CD的对称点A1.②连接A1B交CD于M,则在M处饮水所走路
程最短.
(2)由(1)知:A1C=AC=BD,∠A1CM=∠BDM,∠A1MC=∠BMD,故△A1CM≌△BDM.所以A1M=BM,CM=DM,所以M为CD的中点,AM=500米,
所以A1B=2×500=1000(米).故最短路程为1000米.
7.(2012·随州中考)如图,在△ABC中,
AB=AC,点D是BC的中点,点E在AD上.
试说明(1)△ABD≌△ACD.
(2)BE=CE.
【解析】(1)在△ABD和△ACD中,
因为D是BC的中点,所以BD=CD,因为AB=AC,AD=AD,所以△ABD≌△ACD(SSS).
(2)由(1)知△ABD≌△ACD,所以∠BAD=∠CAD,即∠BAE=∠CAE,
在△ABE和△ACE中,
所以BE=CE.
8.如图,在Rt△ABC中,AB=AC,∠BAC=90°,D为BC的中点.
(1)写出点D到△ABC的三个顶点
A,B,C的距离关系(不要求说明).
(2)如果点M,N分别在线段AB,AC上移动,
在移动中保持AN=BM,请判断△DMN的形状,并说明你的结论.
【解析】(1)DA=DB=DC.
(2)△DMN为等腰直角三角形.
说明:连接AD,因为AB=AC,∠BAC=90°,所以∠B=45°.
又因为D为BC的中点,所以AD平分∠CAB,所以AD⊥BC,∠CAD=45°.
在△ADN和△BDM中,
所以△ADN≌△BDM(SAS),
所以DM=DN,∠NDA=∠BDM.
因为AD⊥BC,所以∠ADB=90°.
因为∠ADB=∠ADM+∠BDM,
所以∠MDN=∠ADM+∠ADN
=∠ADM+∠BDM=90°,
所以△DMN是等腰直角三角形.
谢 谢
