鲁教版(五四制)数学七年级上册 6.4 确定一次函数的表达式教案
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 6.4 确定一次函数的表达式教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 47.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 00:00:00 | ||
图片预览

文档简介
确定一次函数的表达式
【教学目标】
1.了解一个条件确定一个正比例函数,两个条件确定一个一次函数。
2.会用待定系数法求出一次函数和正比例函数表达式。
【教学重难点】
1.重点:会用待定系数法确定一次函数表达式;
2.难点:能够根据一次函数图像或者其他一些情境,熟练灵活地利用待定系数法确定函数的表达式。
【教学过程】
一、回顾导入。
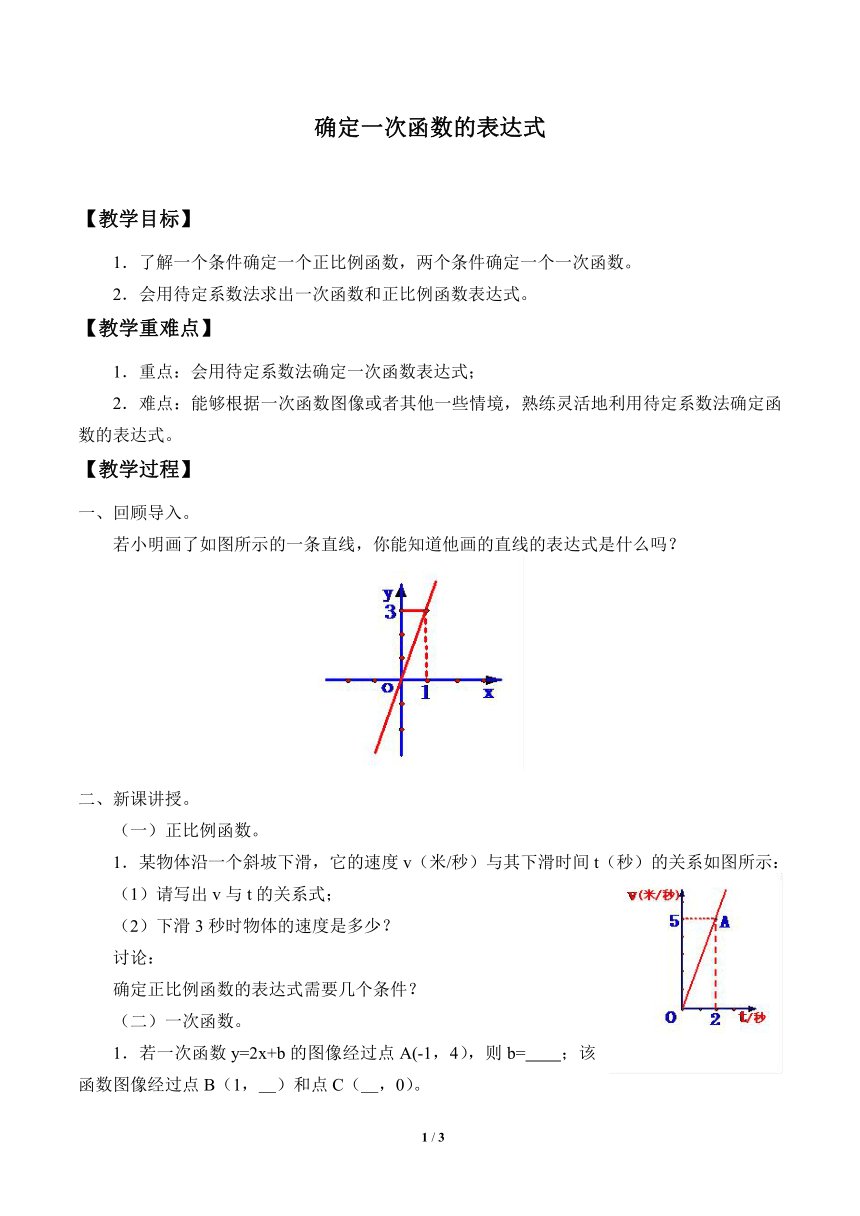
若小明画了如图所示的一条直线,你能知道他画的直线的表达式是什么吗?
二、新课讲授。
(一)正比例函数。
1.某物体沿一个斜坡下滑,它的速度v(米/秒)与其下滑时间t(秒)的关系如图所示:
(1)请写出v与t的关系式;
(2)下滑3秒时物体的速度是多少?
讨论:
确定正比例函数的表达式需要几个条件?
(二)一次函数。
1.若一次函数y=2x+b的图像经过点A(-1,4),则b= ;该函数图像经过点B(1,_)和点C(_,0)。
2.假如又有同学画了如下一条直线,你能知道该函数的表达式吗?
想一想:
确定一次函数的表达式需要几个条件?
(三)例题。
1.在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数。一根弹簧不挂物体时长14.5cm;当所挂物体的质量为3kg时,弹簧长16cm。请写出y与x之间的关系式,并求当所挂物体的质量为4kg时弹簧的长度。
解:设y=kx+b,根据题意,得
(1)14.5=b
(2)16=3k+b
将b=14.5代入(2),得k=0.5.
在弹性限度内,y于x的关系是为:
y=0.5x+14.5
当x=4时,y=0.5×4+14.5=16.5(cm)
即物体的质量为4kg时,弹簧长度为16.5cm。
(四)巩固练习。
练习(A):
1.根据条件确定一次函数的表达式:y是x的正比例函数,当x=2时,y=6,求y与x之间的关系式。
2.直线l是一次函数y=kx+b的图像,
(1)k= ,b= 。
(2)当x=30时,y= 。
(3)当y=30时,x= 。
练习(B):
1.已知,一次函数的图像与直线y=2x平行,且过点(-1,1),试求这个一次函数的表达式。
2.若函数y=kx+b的图像经过点(0,-1),(-3,2),求k,b的值及函数表达式。
提高练习:
1.若直线y=kx+b经过点(0,2),且与坐标轴围成等腰直角三角形,试求该直线的函数表达式。
2.若一次函数y=kx+b的图像经过(-3,2)和(1,6)两点,你能确定该函数的表达式吗?
三、课时小结。
确定一次函数表达式的步骤:
1.设—设函数表达式y=kx+b。
2.代—将已知条件代入y=kx+b中,列出关于k、b的方程。
3.求—解方程,求k、b的值。
4.写—把求出的k、b值代回到表达式中。
在确定函数表达式时,要求几个系数就需要知道几个点的坐标。
【作业布置】
习题6.6第1、2、4题
PAGE
3 / 3
【教学目标】
1.了解一个条件确定一个正比例函数,两个条件确定一个一次函数。
2.会用待定系数法求出一次函数和正比例函数表达式。
【教学重难点】
1.重点:会用待定系数法确定一次函数表达式;
2.难点:能够根据一次函数图像或者其他一些情境,熟练灵活地利用待定系数法确定函数的表达式。
【教学过程】
一、回顾导入。
若小明画了如图所示的一条直线,你能知道他画的直线的表达式是什么吗?
二、新课讲授。
(一)正比例函数。
1.某物体沿一个斜坡下滑,它的速度v(米/秒)与其下滑时间t(秒)的关系如图所示:
(1)请写出v与t的关系式;
(2)下滑3秒时物体的速度是多少?
讨论:
确定正比例函数的表达式需要几个条件?
(二)一次函数。
1.若一次函数y=2x+b的图像经过点A(-1,4),则b= ;该函数图像经过点B(1,_)和点C(_,0)。
2.假如又有同学画了如下一条直线,你能知道该函数的表达式吗?
想一想:
确定一次函数的表达式需要几个条件?
(三)例题。
1.在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数。一根弹簧不挂物体时长14.5cm;当所挂物体的质量为3kg时,弹簧长16cm。请写出y与x之间的关系式,并求当所挂物体的质量为4kg时弹簧的长度。
解:设y=kx+b,根据题意,得
(1)14.5=b
(2)16=3k+b
将b=14.5代入(2),得k=0.5.
在弹性限度内,y于x的关系是为:
y=0.5x+14.5
当x=4时,y=0.5×4+14.5=16.5(cm)
即物体的质量为4kg时,弹簧长度为16.5cm。
(四)巩固练习。
练习(A):
1.根据条件确定一次函数的表达式:y是x的正比例函数,当x=2时,y=6,求y与x之间的关系式。
2.直线l是一次函数y=kx+b的图像,
(1)k= ,b= 。
(2)当x=30时,y= 。
(3)当y=30时,x= 。
练习(B):
1.已知,一次函数的图像与直线y=2x平行,且过点(-1,1),试求这个一次函数的表达式。
2.若函数y=kx+b的图像经过点(0,-1),(-3,2),求k,b的值及函数表达式。
提高练习:
1.若直线y=kx+b经过点(0,2),且与坐标轴围成等腰直角三角形,试求该直线的函数表达式。
2.若一次函数y=kx+b的图像经过(-3,2)和(1,6)两点,你能确定该函数的表达式吗?
三、课时小结。
确定一次函数表达式的步骤:
1.设—设函数表达式y=kx+b。
2.代—将已知条件代入y=kx+b中,列出关于k、b的方程。
3.求—解方程,求k、b的值。
4.写—把求出的k、b值代回到表达式中。
在确定函数表达式时,要求几个系数就需要知道几个点的坐标。
【作业布置】
习题6.6第1、2、4题
PAGE
3 / 3
