24[1].2点线圆与圆的关系导学案(共4课时)
文档属性
| 名称 | 24[1].2点线圆与圆的关系导学案(共4课时) |  | |
| 格式 | zip | ||
| 文件大小 | 330.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-19 21:00:34 | ||
图片预览



文档简介
课题:24.2.1点和圆的位置关系
教与学目标: 1.理解并掌握设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外d>r;点P在圆上d=r;点P在圆内d重点: 点和圆的位置关系的结论:不在同一直线上的三个点确定一个圆其它们的运用
难点: 讲授反证法的证明思路。
自主探究: 学习感悟
自学教材P90-----P92,思考下列问题:1.点与圆的三种位置关系:(圆的半径 r,点P与圆心的距离为d)点P在圆外 ;点P在圆上 ;点P在圆内 ;2.自己作圆:(思考)(1)作经过已知点A的圆,这样的圆能作出多少个?(2)经过A、B两点作圆,这样的圆能作出多少个?它们的圆心分布有什么特点?(3)经过A、B、C三点作圆,有哪些情况?三点应符合什么条件才能作圆? 由以上作圆可知过已知点作圆实质是确定圆心和半径,因此过一点的圆有 个;过两点的圆有 个,圆心在 上;过不在同一条直线上的三点作 个圆,圆心是 ,半径是 .3.什么叫三角形的外接圆?三角形的外心及性质?4.教材是如何用反证法证明过同一直线上的三点不能作圆?反证法的证明思路是什么?
课堂展示: 学习感悟
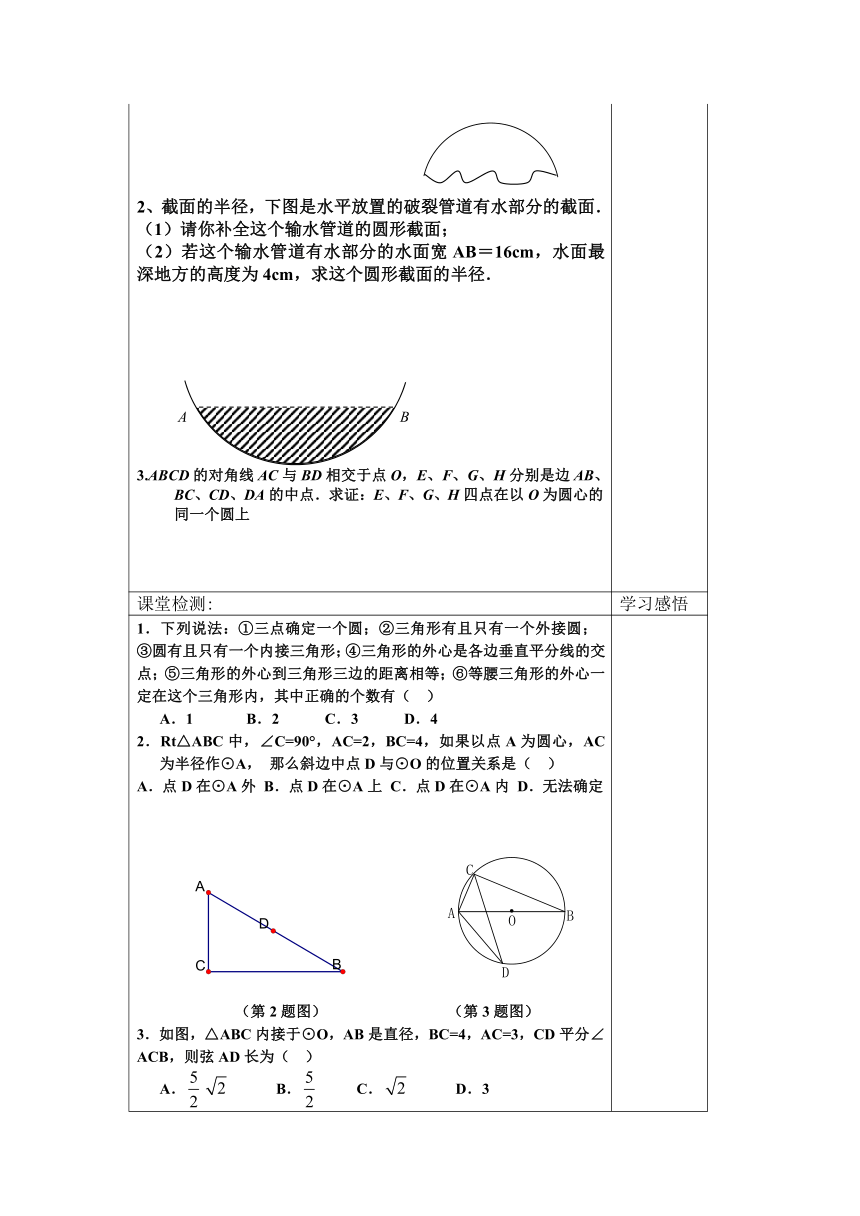
1.某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.(圆心是一个点,一个点可以由两条直线交点而成,因此,只要在残缺的圆盘上任取两条线段,作线段的中垂线,交点就是我们所求的圆心).2、截面的半径,下图是水平放置的破裂管道有水部分的截面.(1)请你补全这个输水管道的圆形截面;(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.3.ABCD的对角线AC与BD相交于点O,E、F、G、H分别是边AB、BC、CD、DA的中点.求证:E、F、G、H四点在以O为圆心的同一个圆上
课堂检测: 学习感悟
1.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③圆有且只有一个内接三角形;④三角形的外心是各边垂直平分线的交点;⑤三角形的外心到三角形三边的距离相等;⑥等腰三角形的外心一定在这个三角形内,其中正确的个数有( ) A.1 B.2 C.3 D.42.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙O的位置关系是( )A.点D在⊙A外 B.点D在⊙A上 C.点D在⊙A内 D.无法确定 (第2题图) (第3题图)3.如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平分∠ACB,则弦AD长为( ) A. B. C. D.34.经过一点P可以作_______个圆;经过两点P、Q可以作________个圆,圆心在_________上;经过不在同一直线上的三个点可以作________个圆,圆心是________的交点.5.在平面内,⊙O的半径为5cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是 .6.直角三角形的外心是______的中点,锐角三角形外心在三角形______,钝角三角形外心在三角形_________.7.已知△ABC的三边长分别为6cm、8cm、10cm,则这个三角形的外接圆的面积为__________cm2.(结果用含π的代数式表示)8.如图,通过防治“非典”,人们增强了卫生意识,大街随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中,如图所示,A、B、C为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,要使得回收站建在三个小区都相等的某处,请问如果你是工程师,你将如何选址.9如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .10.如图,△ABC的外心坐标是_________.11.图所示,在△ABC中,∠C=90°,AC=3,BC=4,以点C位圆心做⊙C,半径为r当r取何值时,点A、B都在⊙C外? (2)当r取何值时,点A⊙C内,点B在⊙C外?
拓展延伸: 学习感悟
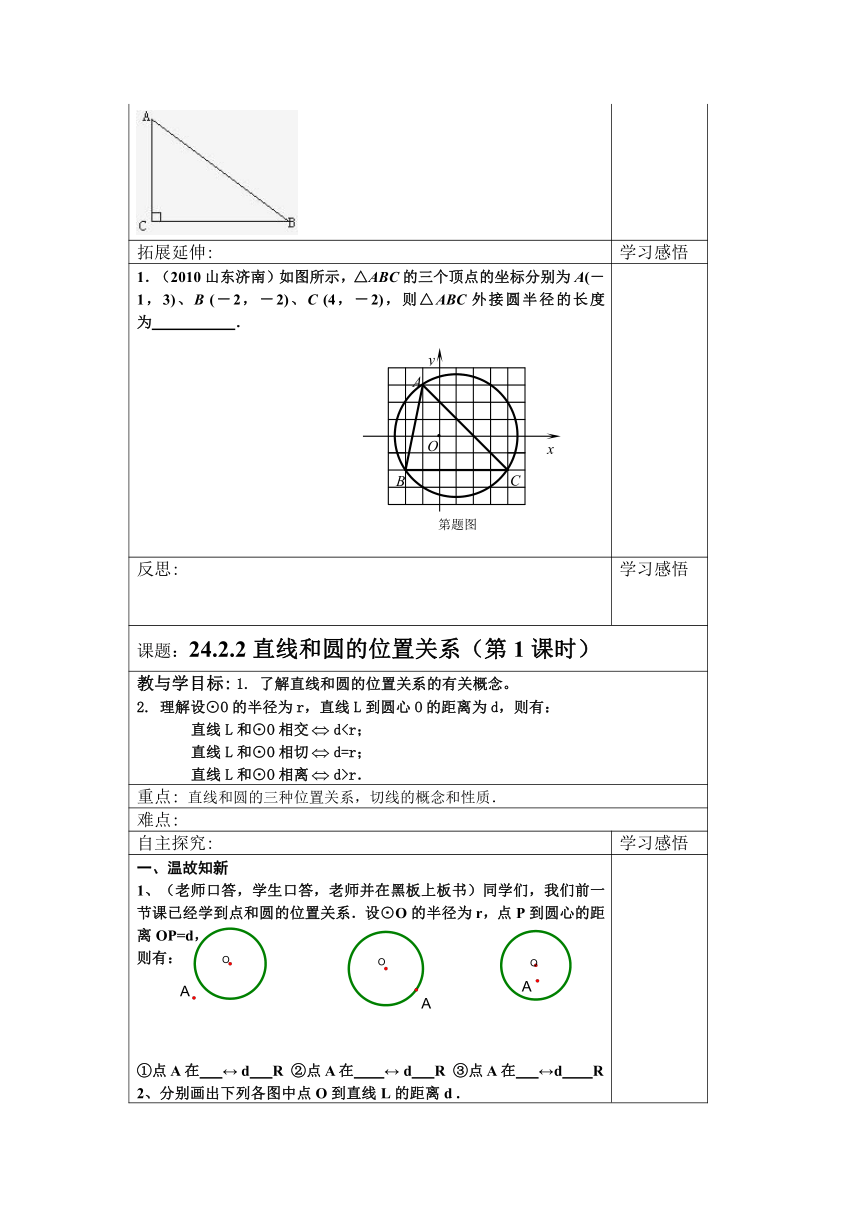
1.(2010山东济南)如图所示,△ABC的三个顶点的坐标分别为A(-1,3)、B (-2,-2)、C (4,-2),则△ABC外接圆半径的长度为 .
反思: 学习感悟
课题:24.2.2直线和圆的位置关系(第1课时)
教与学目标: 1. 了解直线和圆的位置关系的有关概念。2. 理解设⊙O的半径为r,直线L到圆心O的距离为d,则有:直线L和⊙O相交dr.
重点: 直线和圆的三种位置关系,切线的概念和性质.
难点:
自主探究: 学习感悟
一、温故知新1、(老师口答,学生口答,老师并在黑板上板书)同学们,我们前一节课已经学到点和圆的位置关系.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点A在 d R ②点A在 d R ③点A在 d R2、分别画出下列各图中点O到直线L的距离d .自学教材P93---P94思考下列问题:通过教材“观察”及动手操作,判断直线与圆的位置关系?探究1:将⊙沿着箭头的方向平移,从⊙与直线的公共点个数来看,会有哪几种情况. 答:直线和圆的位置关系: 如图1:直线和圆有两个公共点,我们说这条直线和圆 。直线L叫做圆O的 ;如图2:直线和圆有唯一一个公共点,我们说这条直线和圆 ,直线L叫做圆O的 ,这个公共点叫 ;如图3:直线和圆没有公共点,我们说这条直线和圆 。2、利用上面所学的知识填下表:直线和圆的位置关系相 离 . 相 切 .相 交 .公共点个数公共点名称d与R的大小关系直线名称探究2:类比点与圆的位置关系,从圆心到直线的距离()与半径()的大小关系来确定直线与圆的位置关系:⑴直线与圆相交;⑵直线与圆相切;⑶直线与圆相离.
课堂展示: 学习感悟
圆的直径是13,如果直线与圆心的距离分别为如下各数,判断直线与圆的位置关系?并说明公共点的个数.⑴ 4.5 ⑵ 6.5 ⑶ 8答:2、如图,已知的斜边,.⑴ 以点为圆心作圆,当半径为多长时,直线与⊙相切?为什么?⑵ 以点为圆心,分别以2cm和4cm为半径作两个圆,这两个圆与直线分别有怎样的位置关系?
课堂检测: 学习感悟
1、Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,给出下列三个结论:①以点C为圆心,2.3cm长为半径的圆与AB相离;②以点C为圆心,2.4cm长为半径的圆与AB相切;③以点C为圆心,2.5cm长为半径的圆与AB相交,则上述结论正确的有( )A.0个 B.1个 C.2个 D.3个2.如图梯形ABCD,AB‖CD,AB=,∠B=30°有一个直径等于3的圆,其圆心O在BC边上移动,当BO等于多少时,⊙O与BA相切?3、如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )A.点(0,3)B. 点(2,3) C.点(5,1) D. 点(6,1)4.知⊙O的直径为12cm①若圆心O到直线l的距离为12cm,则直线l与⊙O 的位置关系为________;②若圆心O到直线l的距离为6cm,则直线l与⊙O 的位置关系为________;③若圆心O到直线l的距离为3cm,则直线l与 ⊙O 的位置关系为________.⑵已知⊙O的直径为10cm.①若直线l与⊙O相交,则圆心O到直线l的距离d ________;②若直线l与⊙O相切,则圆心O到直线l的距离d ________;③若直线l与⊙O相离,则圆心O到直线l的距离d ________.⑶如果⊙O的直径为10厘米,圆心O到直线AB的距离为10厘米,那么⊙O 与直线A B有怎样的位置关系?4.如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心P在射线OA上,点P与点O的距离为8cm,如果⊙P以2cm/s的速度由A向B运动,那么3或5s时⊙P与直线CD相切.
反思: 学习感悟
课题:24.2.2直线圆的位置关系(第2课时)
教与学目标:3. 理解切线的判定定理、理解切线的性质定理并熟练掌握以上内容解决一些实际问题。
重点: 切线的判定定理;切线的性质定理及其运用它们解决一些具体的题目。
难点: 由上节课点和圆的位置关系迁移并运动直线导出直线和圆的位置关系的三个对应等价。
自主探究: 学习感悟
1、直线与圆的位置关系有几种?分别是那些关系?直线与圆的位置关系的判断方法有哪几种 2、直线与圆相切有哪几种判断方法?3、思考作图:已知:点A为⊙o上的一点,如和过点A作⊙o的切线呢?交流总结:根据直线要想与圆相切必须d=r,所以连接OA过A点作OA的垂线如图1,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系 从作图中可以得出:经过_________________并且___________与这条半径的的直线是圆的切线思考:如图所示,它的数学语言该怎样表示呢?4、例题精析:例1、(教材103页例1)如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证直线AB是⊙O的切线。例2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系, 并证明你的结论。(无点作垂线证半径)
课堂展示: 学习感悟
1.如图,AB是⊙O的直径,点C在⊙O上,AC平分∠DAB ,AD⊥CD。求证:CD与⊙O相切。2.如图,AB是⊙O的直径,点D在⊙O上,BC是⊙O的切线,AD∥OC。求证:CD是⊙O的切线。3.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC。求证:⑴ 点D是BC的中点; ⑵ DE是⊙O的切线。4图在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A.与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.(1)试判断BC所在直线与小圆的位置关系,并说明理由;(2)试判断线段AC.AD.BC之间的数量关系,并说明理由;(3)若,求大圆与小圆围成的圆环的面积.(结果保留π)
课堂检测: 学习感悟
5.如图,已知PA是⊙O的切线,切点为A,PA = 3,∠APO = 30°,那么OP = .6.如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当OM=______cm时,⊙M与OA相切.1. (2011·菏泽中考)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.(1)求证:△ABE∽△ADB.(2)求AB的长;(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.2.、如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.3.如图,已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连接AD并延长交BC于点E,BC=3,CD=2
(1)求⊙O的半径.
(2)取BE的中点F,连接DF,求证:DF是⊙O的切线.
4.如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连结AD交OB于点E。求证:CD=CE5.如图所示,AB是⊙O的直径,CD切⊙O于点C,AD⊥CD。求证:AC平分∠DAB。
反思: 学习感悟
课题:24.2.2直线圆的位置关系(第3课时)
教与学目标:理解切线的性质定理并熟练掌握以上内容解决一些实际问题。
重点: 切线的性质定理及其运用它们解决一些具体的题目
难点: 切线的性质定理及其运用
自主探究: 学习感悟
探究3:如图,点在⊙上,请过点画一条直线,使得,判断直线与⊙的位置关系. 把探究3的问题反过来,即如果直线l是⊙的切线,切点是A,那么半径OA与直线l是不是一定垂直呢?——由此得切线的性质定理:
课堂展示: 学习感悟
1.如图,两个同心圆O,大圆的弦AB切小圆于点C。求证:点C是AB的中点。2.如图,两个同心圆O,大圆的弦AB、AC切小圆于点M、N,连结BC、MN。求证:MN=BC。 如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连结AD交OB于点E。求证:CD=CE
课堂检测: 学习感悟
1(2010哈尔滨)5.如图,PA、PB是O的切线,切点分别是A、B,如果∠P=60°,那么∠AOB等于( ) A.60° B.90° C.120° D.150°2、(2011江苏宿迁,17,3分)如下第1图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=26°,则∠ACB的度数为 .3(2011四川南充市,13,3分)如上第2图,PA,PB是⊙O是切线,A,B为切点, AC是⊙O的直径,若∠BAC=25°,则∠P= __________度.4.下列说法正确的是( ) A.与圆有公共点的直线是圆的切线. B.和圆心距离等于圆的半径的直线是圆的切线; C.垂直于圆的半径的直线是圆的切线; D.过圆的半径的外端的直线是圆的切线如图,AB与⊙O切于点C,OA=OB,若⊙O的直径为8cm,AB=10那么OA的长是( )A. B.6.如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为 ( ) A. B. C.2 D. 4(第5题图) (第6题图) 7如图,AB为圆O的直径,C为圆O上一点,AD和过C点的切线线互相垂直,垂足为D,求证AC平分∠DAB,8.如图,已知PA是⊙O的切线,切点为A,PA = 3,∠APO = 30°,那么OP = .9.如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当OM=______cm时,⊙M与OA相切. (第10题图) (第6题图) 10.如图,PA是⊙O的切线,切点是A,过点A作AH⊥OP于点H,交⊙O于点B。求证:PB是⊙O的切线。5(桂林2010)25.(本题满分10分)如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.(1)证明:AF平分∠BAC;(2)证明:BF=FD;(3)若EF=4,DE=3,求AD的长.(现在不做)
拓展延伸: 学习感悟
1.如图,P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,弦AB与PO交于C,⊙O半径为1,PO=2,则PA_______,PB=________,PC=_______AC=______,BC=______∠AOB=________.
反思: 学习感悟
课题:24.2.2直线圆的位置关系(第3课时)
教与学目标: 1.了解切线长的概念2.理解切线长定理 3.了解三角形的内切圆和三角形的内心的概念,熟练掌握它的应用
重点: 切线长定理及其运用
难点: 切线长定理的导出及其证明和运用切线长定理解决一些实际问题.
自主探究: 学习感悟
1、切线的判定定理
2、切线的性质
如果一条直线符合下列三个条件中的任意两个,那么它一定满足第三个条件。这三个条件是:(1)过圆心;(2)过切点;(3)垂直于切线。
3.已知△ABC,作三个内角平分线,说说它具有什么性质?(二) 学生探究 教师引领问题1:如图,纸上有一⊙O,PA为⊙O的一条切线,沿着直线PO将纸对折,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的切线吗?利用图形的轴对称性,说明图中的PA与PB,∠APO与∠BPO有说明关系?经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到的 如上图,PA、PB是⊙O的两条切线,∴OA⊥AP, OB⊥BP.又OA=OB, OP=OP,在Rt△AOP和Rt△BOP中 ∴Rt△AOP≌Rt△BOP( )∴PA=PB, ∠OPA=∠OPB( )由此得到切线长定理: 从圆外一点可以引圆的两条 ,它们的切线长 ,这一点和圆心的连线 两条切线的 . 思考2:如图,是一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?(提示:假设符合条件的圆已经做出,那么它应当与三角形的三条边都相切,这个圆的圆心到三角形的三条边的距离都等于半径。如何找到这个圆心呢?).并得出结论:与三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心是三角形三条 的交点,叫做三角形的内心。它到三边的 距离 。例1:如图△ABC的内切圆⊙O与BC、CA、AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长. (三)学生归纳 教师提炼
课堂展示: 学习感悟
四)学生展示 教师激励例1.如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且△ABC的面积为6.求内切圆的半径r.2.如图,△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠AOC的度数。
课堂检测: 学习感悟
(五)学生达标 教师测评1、从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( ). A.9 B.9(-1) C.9(-1) D.92、如图1,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ). A.60° B.75° C.105° D.120°(1) (2) 3.如图2,圆O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.,AC=6,BC=8,求△ABC的内切圆半径 。4、如图,PA、PB是⊙O的两条切线,A、B为切点,求证∠ABO=∠APB.5、如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且△ABC的面积为6.求内切圆的半径r.6.P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,弦AB与PO交于C,⊙O半径为1,PO=2,则PA_______,PB=________,PC=_______AC=______,BC=______∠AOB=________.7.PA、PB分别与圆O相切于点A、B,若∠APB=60°,点C是异与AB的任意一点,则∠ACB的度数,若PA=求圆的半径。8、PA、PB是圆O的切线,CD切圆O于点E,PA=6CM求△PDC的周长9.如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,若OB=6cm,OC=8cm,求(1)∠BOC的度数,(2)⊙O的半径(3)BE+CG的长
拓展延伸: 学习感悟
1.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )A.180°-a B.90°-a C.90°+a D.180°-2a
反思: 学习感悟
课题:24.2.3点、直线、圆和圆的位置关系(第4课时)
教与学目标: 1. 了解两个圆相离(外离、内含),两个圆相切(外切、内切),两圆相交、圆心距等概念。2. 理解两圆的 位置 关系与d、r 1 、r 2 等量关系的等价条件并灵活应用它们解题。3. 通过复习直线和圆的位置关系和结合操作几何,迁移到圆与圆之间的五种关系并运用它们解决一些具体的题目。
重点:两个圆的五种位置关系中的等价条件及它们的运用
难点: 探索两个圆之间的五种关系的等价条件及应用它们解题。
自主探究: 学习感悟
(一)探究:圆与圆的位置关系:如图,将⊙向右平移,⊙不动.你能发现⊙和⊙有哪几种不同的位置关系?每种位置关系中两圆公共点的个数分别是多少?结论:1.相离: 2.相切: 3.相交:二)探究:设⊙、⊙的半径分别为、,圆心距,利用与、之间的关系讨论两圆的位置关系.⑴外离: ,⑵外切: ,⑶相交: ,⑷内切: ,⑸内含: .(三)探究:相切两圆组成的图形是轴对称图形吗?如果是,它的对称轴是什么?切点与对称轴有什么位置关系?相交两圆呢?你从中得到什么结论?例1.如图,⊙O的半径为5cm,点P是⊙O外一点,OP=8cm,以P为圆心作一个圆与⊙O外切,这个圆的半径应是多少?以P为圆心作一个圆与⊙O内切呢?
课堂展示: 学习感悟
1: 如图所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm, 求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少? (2)作⊙A与⊙O相内切,并求出此时⊙A的半径. 2(2010,安徽芜湖)若两圆相切,圆心距是7,其中一圆的半径为10,则另一圆的半径为_______.3.(2011江苏南京,26,8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
课堂检测: 学习感悟
1.(2010年兰州)6.已知两圆的半径R、r分别为方程的两根,两圆的圆心距为1,两圆的位置关系是( ) A.外离 B.内切 C.相交 D.外切2.(2010宁波市)6.两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是 ( ) A.内切 B.相交 C.外切 D.外离3.(2010年无锡)6.已知两圆内切,它们的半径分别为3和6,则这两圆的圆心距d的取值满足 ( )A. B. C. D.4..(2010年长沙)已知⊙O1、⊙O2的半径分别是、,若两圆相交,则圆心距O1O2可能取的值是 ( )A.2 B.4 C.6 D.85.. (2010年金华) 如果半径为3cm的⊙O1与半径为4cm的⊙O2内切,那么两圆的圆心距O1O2= cm.7.已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系是( )(A)相交 (B)外切 (C)外离 (D)内含8.(2010年眉山)4.⊙O1的半径为3cm,⊙O2的半径为5cm,圆心距O1O2=2cm,这两圆的位置关系是( )A.外切 B.相交 C.内切 D.内含9.(2010年常州)若两圆的半径分别为2和3,圆心距为5,则两圆的位置关系为( )A.外离 B.外切 C.相交 D.内切10.(2010株洲市)两圆的圆心距,它们的半径分别是一元二次方程的两个根,这两圆的位置关系是 .11.如图是一个五环图案,它由五个圆组成,下排的两个圆的位置关系是 ( ). A.内含 B.外切 C.相交 D.外离 ( 第11题图) ( 第 13题图) ( 第 14 题图) 12 .已知 ⊙ A 与⊙ B 相切,两圆的圆心距为 8㎝, ⊙ A 的半径为 3㎝,则 ⊙ B 的半径( ) A 、5㎝ B、 11 ㎝ C、3㎝ D、5㎝或 11 ㎝ 13 .如图所示,两个等圆 ⊙ O 和 ⊙ O 1 相切,过 O 作 ⊙ O 1 的两条切线 OA 、 OB,A 、B为切点,则∠ AOB= __________ 14. 如图, B 是线段 AC 上的一点,且 AB : AC=2 : 5 ,分别以 AB 、 AC 为直径画圆,则小圆的面积与大圆的面积之比为 _______ . 15.已知 ∠ AOB=30° , C 是射线 OB 上的一点,且 OC=4 ,若以 C 为圆心, r 为半径的圆与射线 OA 有两个不同的交点,则 r 的取值范围是 _______ 16.(益阳市2010年中考题12).如图,分别以A、B为圆心,线段AB的长为半径的两个圆相交于C、D两点,则∠CAD的度数为 .17. (上海)已知圆O1、圆O2的半径不相等,圆O1的半径长为3,若圆O2上的点A满足AO1 = 3,则圆O1与圆O2的位置关系是( )A.相交或相切 B.相切或相离 C.相交或内含 D.相切或内含18.(2010年济宁市)已知⊙O1与⊙O2相切,⊙O1的半径为3 cm,⊙O2的半径为2 cm,则O1O2的长是( )A.1 cm B.5 cm C.1 cm或5 cm D.0.5cm或2.5cm19(2009年重庆市江津区)如图,在10×6的网格图中(每个小正方形的边长均为1个单位长)。⊙A半径为2,⊙B半径为1,需使⊙A与静止的⊙B相切,那么⊙A由图示的位置向左平移 个单位长.
拓展延伸: 学习感悟
如图,轮椅车的大小两车轮(在同一平面上)与地面的触点 间距离为 80cm ,两车轮的直径分别为 136cm , 16cm ,则此两车轮的圆心相距 cm . 2.一个圆环的面积为9 ,大圆的弦 AB 切小圆于点 C ,则弦AB=_____。 (第 2 题图)
反思: 学习感悟
B
A
O
x
y
B
C
A
A
B
C
O
x
第题图
y
O
1
A
C
B
1
x
y
第10题图
A
B
P
O
H
H
A
B
C
P
Q
O
(第题)
(第1题图)
A
B
教与学目标: 1.理解并掌握设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外d>r;点P在圆上d=r;点P在圆内d
难点: 讲授反证法的证明思路。
自主探究: 学习感悟
自学教材P90-----P92,思考下列问题:1.点与圆的三种位置关系:(圆的半径 r,点P与圆心的距离为d)点P在圆外 ;点P在圆上 ;点P在圆内 ;2.自己作圆:(思考)(1)作经过已知点A的圆,这样的圆能作出多少个?(2)经过A、B两点作圆,这样的圆能作出多少个?它们的圆心分布有什么特点?(3)经过A、B、C三点作圆,有哪些情况?三点应符合什么条件才能作圆? 由以上作圆可知过已知点作圆实质是确定圆心和半径,因此过一点的圆有 个;过两点的圆有 个,圆心在 上;过不在同一条直线上的三点作 个圆,圆心是 ,半径是 .3.什么叫三角形的外接圆?三角形的外心及性质?4.教材是如何用反证法证明过同一直线上的三点不能作圆?反证法的证明思路是什么?
课堂展示: 学习感悟
1.某地出土一明代残破圆形瓷盘,如图所示.为复制该瓷盘确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心.(圆心是一个点,一个点可以由两条直线交点而成,因此,只要在残缺的圆盘上任取两条线段,作线段的中垂线,交点就是我们所求的圆心).2、截面的半径,下图是水平放置的破裂管道有水部分的截面.(1)请你补全这个输水管道的圆形截面;(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.3.ABCD的对角线AC与BD相交于点O,E、F、G、H分别是边AB、BC、CD、DA的中点.求证:E、F、G、H四点在以O为圆心的同一个圆上
课堂检测: 学习感悟
1.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③圆有且只有一个内接三角形;④三角形的外心是各边垂直平分线的交点;⑤三角形的外心到三角形三边的距离相等;⑥等腰三角形的外心一定在这个三角形内,其中正确的个数有( ) A.1 B.2 C.3 D.42.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙O的位置关系是( )A.点D在⊙A外 B.点D在⊙A上 C.点D在⊙A内 D.无法确定 (第2题图) (第3题图)3.如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平分∠ACB,则弦AD长为( ) A. B. C. D.34.经过一点P可以作_______个圆;经过两点P、Q可以作________个圆,圆心在_________上;经过不在同一直线上的三个点可以作________个圆,圆心是________的交点.5.在平面内,⊙O的半径为5cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是 .6.直角三角形的外心是______的中点,锐角三角形外心在三角形______,钝角三角形外心在三角形_________.7.已知△ABC的三边长分别为6cm、8cm、10cm,则这个三角形的外接圆的面积为__________cm2.(结果用含π的代数式表示)8.如图,通过防治“非典”,人们增强了卫生意识,大街随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中,如图所示,A、B、C为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见,要使得回收站建在三个小区都相等的某处,请问如果你是工程师,你将如何选址.9如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 .10.如图,△ABC的外心坐标是_________.11.图所示,在△ABC中,∠C=90°,AC=3,BC=4,以点C位圆心做⊙C,半径为r当r取何值时,点A、B都在⊙C外? (2)当r取何值时,点A⊙C内,点B在⊙C外?
拓展延伸: 学习感悟
1.(2010山东济南)如图所示,△ABC的三个顶点的坐标分别为A(-1,3)、B (-2,-2)、C (4,-2),则△ABC外接圆半径的长度为 .
反思: 学习感悟
课题:24.2.2直线和圆的位置关系(第1课时)
教与学目标: 1. 了解直线和圆的位置关系的有关概念。2. 理解设⊙O的半径为r,直线L到圆心O的距离为d,则有:直线L和⊙O相交d
重点: 直线和圆的三种位置关系,切线的概念和性质.
难点:
自主探究: 学习感悟
一、温故知新1、(老师口答,学生口答,老师并在黑板上板书)同学们,我们前一节课已经学到点和圆的位置关系.设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点A在 d R ②点A在 d R ③点A在 d R2、分别画出下列各图中点O到直线L的距离d .自学教材P93---P94思考下列问题:通过教材“观察”及动手操作,判断直线与圆的位置关系?探究1:将⊙沿着箭头的方向平移,从⊙与直线的公共点个数来看,会有哪几种情况. 答:直线和圆的位置关系: 如图1:直线和圆有两个公共点,我们说这条直线和圆 。直线L叫做圆O的 ;如图2:直线和圆有唯一一个公共点,我们说这条直线和圆 ,直线L叫做圆O的 ,这个公共点叫 ;如图3:直线和圆没有公共点,我们说这条直线和圆 。2、利用上面所学的知识填下表:直线和圆的位置关系相 离 . 相 切 .相 交 .公共点个数公共点名称d与R的大小关系直线名称探究2:类比点与圆的位置关系,从圆心到直线的距离()与半径()的大小关系来确定直线与圆的位置关系:⑴直线与圆相交;⑵直线与圆相切;⑶直线与圆相离.
课堂展示: 学习感悟
圆的直径是13,如果直线与圆心的距离分别为如下各数,判断直线与圆的位置关系?并说明公共点的个数.⑴ 4.5 ⑵ 6.5 ⑶ 8答:2、如图,已知的斜边,.⑴ 以点为圆心作圆,当半径为多长时,直线与⊙相切?为什么?⑵ 以点为圆心,分别以2cm和4cm为半径作两个圆,这两个圆与直线分别有怎样的位置关系?
课堂检测: 学习感悟
1、Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,给出下列三个结论:①以点C为圆心,2.3cm长为半径的圆与AB相离;②以点C为圆心,2.4cm长为半径的圆与AB相切;③以点C为圆心,2.5cm长为半径的圆与AB相交,则上述结论正确的有( )A.0个 B.1个 C.2个 D.3个2.如图梯形ABCD,AB‖CD,AB=,∠B=30°有一个直径等于3的圆,其圆心O在BC边上移动,当BO等于多少时,⊙O与BA相切?3、如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )A.点(0,3)B. 点(2,3) C.点(5,1) D. 点(6,1)4.知⊙O的直径为12cm①若圆心O到直线l的距离为12cm,则直线l与⊙O 的位置关系为________;②若圆心O到直线l的距离为6cm,则直线l与⊙O 的位置关系为________;③若圆心O到直线l的距离为3cm,则直线l与 ⊙O 的位置关系为________.⑵已知⊙O的直径为10cm.①若直线l与⊙O相交,则圆心O到直线l的距离d ________;②若直线l与⊙O相切,则圆心O到直线l的距离d ________;③若直线l与⊙O相离,则圆心O到直线l的距离d ________.⑶如果⊙O的直径为10厘米,圆心O到直线AB的距离为10厘米,那么⊙O 与直线A B有怎样的位置关系?4.如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心P在射线OA上,点P与点O的距离为8cm,如果⊙P以2cm/s的速度由A向B运动,那么3或5s时⊙P与直线CD相切.
反思: 学习感悟
课题:24.2.2直线圆的位置关系(第2课时)
教与学目标:3. 理解切线的判定定理、理解切线的性质定理并熟练掌握以上内容解决一些实际问题。
重点: 切线的判定定理;切线的性质定理及其运用它们解决一些具体的题目。
难点: 由上节课点和圆的位置关系迁移并运动直线导出直线和圆的位置关系的三个对应等价。
自主探究: 学习感悟
1、直线与圆的位置关系有几种?分别是那些关系?直线与圆的位置关系的判断方法有哪几种 2、直线与圆相切有哪几种判断方法?3、思考作图:已知:点A为⊙o上的一点,如和过点A作⊙o的切线呢?交流总结:根据直线要想与圆相切必须d=r,所以连接OA过A点作OA的垂线如图1,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l和⊙O有什么位置关系 从作图中可以得出:经过_________________并且___________与这条半径的的直线是圆的切线思考:如图所示,它的数学语言该怎样表示呢?4、例题精析:例1、(教材103页例1)如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证直线AB是⊙O的切线。例2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系, 并证明你的结论。(无点作垂线证半径)
课堂展示: 学习感悟
1.如图,AB是⊙O的直径,点C在⊙O上,AC平分∠DAB ,AD⊥CD。求证:CD与⊙O相切。2.如图,AB是⊙O的直径,点D在⊙O上,BC是⊙O的切线,AD∥OC。求证:CD是⊙O的切线。3.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC。求证:⑴ 点D是BC的中点; ⑵ DE是⊙O的切线。4图在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A.与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.(1)试判断BC所在直线与小圆的位置关系,并说明理由;(2)试判断线段AC.AD.BC之间的数量关系,并说明理由;(3)若,求大圆与小圆围成的圆环的面积.(结果保留π)
课堂检测: 学习感悟
5.如图,已知PA是⊙O的切线,切点为A,PA = 3,∠APO = 30°,那么OP = .6.如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当OM=______cm时,⊙M与OA相切.1. (2011·菏泽中考)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.(1)求证:△ABE∽△ADB.(2)求AB的长;(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.2.、如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.3.如图,已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连接AD并延长交BC于点E,BC=3,CD=2
(1)求⊙O的半径.
(2)取BE的中点F,连接DF,求证:DF是⊙O的切线.
4.如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连结AD交OB于点E。求证:CD=CE5.如图所示,AB是⊙O的直径,CD切⊙O于点C,AD⊥CD。求证:AC平分∠DAB。
反思: 学习感悟
课题:24.2.2直线圆的位置关系(第3课时)
教与学目标:理解切线的性质定理并熟练掌握以上内容解决一些实际问题。
重点: 切线的性质定理及其运用它们解决一些具体的题目
难点: 切线的性质定理及其运用
自主探究: 学习感悟
探究3:如图,点在⊙上,请过点画一条直线,使得,判断直线与⊙的位置关系. 把探究3的问题反过来,即如果直线l是⊙的切线,切点是A,那么半径OA与直线l是不是一定垂直呢?——由此得切线的性质定理:
课堂展示: 学习感悟
1.如图,两个同心圆O,大圆的弦AB切小圆于点C。求证:点C是AB的中点。2.如图,两个同心圆O,大圆的弦AB、AC切小圆于点M、N,连结BC、MN。求证:MN=BC。 如图,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连结AD交OB于点E。求证:CD=CE
课堂检测: 学习感悟
1(2010哈尔滨)5.如图,PA、PB是O的切线,切点分别是A、B,如果∠P=60°,那么∠AOB等于( ) A.60° B.90° C.120° D.150°2、(2011江苏宿迁,17,3分)如下第1图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=26°,则∠ACB的度数为 .3(2011四川南充市,13,3分)如上第2图,PA,PB是⊙O是切线,A,B为切点, AC是⊙O的直径,若∠BAC=25°,则∠P= __________度.4.下列说法正确的是( ) A.与圆有公共点的直线是圆的切线. B.和圆心距离等于圆的半径的直线是圆的切线; C.垂直于圆的半径的直线是圆的切线; D.过圆的半径的外端的直线是圆的切线如图,AB与⊙O切于点C,OA=OB,若⊙O的直径为8cm,AB=10那么OA的长是( )A. B.6.如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为 ( ) A. B. C.2 D. 4(第5题图) (第6题图) 7如图,AB为圆O的直径,C为圆O上一点,AD和过C点的切线线互相垂直,垂足为D,求证AC平分∠DAB,8.如图,已知PA是⊙O的切线,切点为A,PA = 3,∠APO = 30°,那么OP = .9.如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当OM=______cm时,⊙M与OA相切. (第10题图) (第6题图) 10.如图,PA是⊙O的切线,切点是A,过点A作AH⊥OP于点H,交⊙O于点B。求证:PB是⊙O的切线。5(桂林2010)25.(本题满分10分)如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.(1)证明:AF平分∠BAC;(2)证明:BF=FD;(3)若EF=4,DE=3,求AD的长.(现在不做)
拓展延伸: 学习感悟
1.如图,P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,弦AB与PO交于C,⊙O半径为1,PO=2,则PA_______,PB=________,PC=_______AC=______,BC=______∠AOB=________.
反思: 学习感悟
课题:24.2.2直线圆的位置关系(第3课时)
教与学目标: 1.了解切线长的概念2.理解切线长定理 3.了解三角形的内切圆和三角形的内心的概念,熟练掌握它的应用
重点: 切线长定理及其运用
难点: 切线长定理的导出及其证明和运用切线长定理解决一些实际问题.
自主探究: 学习感悟
1、切线的判定定理
2、切线的性质
如果一条直线符合下列三个条件中的任意两个,那么它一定满足第三个条件。这三个条件是:(1)过圆心;(2)过切点;(3)垂直于切线。
3.已知△ABC,作三个内角平分线,说说它具有什么性质?(二) 学生探究 教师引领问题1:如图,纸上有一⊙O,PA为⊙O的一条切线,沿着直线PO将纸对折,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的切线吗?利用图形的轴对称性,说明图中的PA与PB,∠APO与∠BPO有说明关系?经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到的 如上图,PA、PB是⊙O的两条切线,∴OA⊥AP, OB⊥BP.又OA=OB, OP=OP,在Rt△AOP和Rt△BOP中 ∴Rt△AOP≌Rt△BOP( )∴PA=PB, ∠OPA=∠OPB( )由此得到切线长定理: 从圆外一点可以引圆的两条 ,它们的切线长 ,这一点和圆心的连线 两条切线的 . 思考2:如图,是一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?(提示:假设符合条件的圆已经做出,那么它应当与三角形的三条边都相切,这个圆的圆心到三角形的三条边的距离都等于半径。如何找到这个圆心呢?).并得出结论:与三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心是三角形三条 的交点,叫做三角形的内心。它到三边的 距离 。例1:如图△ABC的内切圆⊙O与BC、CA、AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长. (三)学生归纳 教师提炼
课堂展示: 学习感悟
四)学生展示 教师激励例1.如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且△ABC的面积为6.求内切圆的半径r.2.如图,△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠AOC的度数。
课堂检测: 学习感悟
(五)学生达标 教师测评1、从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为( ). A.9 B.9(-1) C.9(-1) D.92、如图1,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ). A.60° B.75° C.105° D.120°(1) (2) 3.如图2,圆O内切Rt△ABC,切点分别是D、E、F,则四边形OECF是_______.,AC=6,BC=8,求△ABC的内切圆半径 。4、如图,PA、PB是⊙O的两条切线,A、B为切点,求证∠ABO=∠APB.5、如图,已知⊙O是△ABC的内切圆,切点为D、E、F,如果AE=1,CD=2,BF=3,且△ABC的面积为6.求内切圆的半径r.6.P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,弦AB与PO交于C,⊙O半径为1,PO=2,则PA_______,PB=________,PC=_______AC=______,BC=______∠AOB=________.7.PA、PB分别与圆O相切于点A、B,若∠APB=60°,点C是异与AB的任意一点,则∠ACB的度数,若PA=求圆的半径。8、PA、PB是圆O的切线,CD切圆O于点E,PA=6CM求△PDC的周长9.如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,若OB=6cm,OC=8cm,求(1)∠BOC的度数,(2)⊙O的半径(3)BE+CG的长
拓展延伸: 学习感悟
1.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,若∠ACB=a,则∠APB=( )A.180°-a B.90°-a C.90°+a D.180°-2a
反思: 学习感悟
课题:24.2.3点、直线、圆和圆的位置关系(第4课时)
教与学目标: 1. 了解两个圆相离(外离、内含),两个圆相切(外切、内切),两圆相交、圆心距等概念。2. 理解两圆的 位置 关系与d、r 1 、r 2 等量关系的等价条件并灵活应用它们解题。3. 通过复习直线和圆的位置关系和结合操作几何,迁移到圆与圆之间的五种关系并运用它们解决一些具体的题目。
重点:两个圆的五种位置关系中的等价条件及它们的运用
难点: 探索两个圆之间的五种关系的等价条件及应用它们解题。
自主探究: 学习感悟
(一)探究:圆与圆的位置关系:如图,将⊙向右平移,⊙不动.你能发现⊙和⊙有哪几种不同的位置关系?每种位置关系中两圆公共点的个数分别是多少?结论:1.相离: 2.相切: 3.相交:二)探究:设⊙、⊙的半径分别为、,圆心距,利用与、之间的关系讨论两圆的位置关系.⑴外离: ,⑵外切: ,⑶相交: ,⑷内切: ,⑸内含: .(三)探究:相切两圆组成的图形是轴对称图形吗?如果是,它的对称轴是什么?切点与对称轴有什么位置关系?相交两圆呢?你从中得到什么结论?例1.如图,⊙O的半径为5cm,点P是⊙O外一点,OP=8cm,以P为圆心作一个圆与⊙O外切,这个圆的半径应是多少?以P为圆心作一个圆与⊙O内切呢?
课堂展示: 学习感悟
1: 如图所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm, 求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少? (2)作⊙A与⊙O相内切,并求出此时⊙A的半径. 2(2010,安徽芜湖)若两圆相切,圆心距是7,其中一圆的半径为10,则另一圆的半径为_______.3.(2011江苏南京,26,8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
课堂检测: 学习感悟
1.(2010年兰州)6.已知两圆的半径R、r分别为方程的两根,两圆的圆心距为1,两圆的位置关系是( ) A.外离 B.内切 C.相交 D.外切2.(2010宁波市)6.两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是 ( ) A.内切 B.相交 C.外切 D.外离3.(2010年无锡)6.已知两圆内切,它们的半径分别为3和6,则这两圆的圆心距d的取值满足 ( )A. B. C. D.4..(2010年长沙)已知⊙O1、⊙O2的半径分别是、,若两圆相交,则圆心距O1O2可能取的值是 ( )A.2 B.4 C.6 D.85.. (2010年金华) 如果半径为3cm的⊙O1与半径为4cm的⊙O2内切,那么两圆的圆心距O1O2= cm.7.已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系是( )(A)相交 (B)外切 (C)外离 (D)内含8.(2010年眉山)4.⊙O1的半径为3cm,⊙O2的半径为5cm,圆心距O1O2=2cm,这两圆的位置关系是( )A.外切 B.相交 C.内切 D.内含9.(2010年常州)若两圆的半径分别为2和3,圆心距为5,则两圆的位置关系为( )A.外离 B.外切 C.相交 D.内切10.(2010株洲市)两圆的圆心距,它们的半径分别是一元二次方程的两个根,这两圆的位置关系是 .11.如图是一个五环图案,它由五个圆组成,下排的两个圆的位置关系是 ( ). A.内含 B.外切 C.相交 D.外离 ( 第11题图) ( 第 13题图) ( 第 14 题图) 12 .已知 ⊙ A 与⊙ B 相切,两圆的圆心距为 8㎝, ⊙ A 的半径为 3㎝,则 ⊙ B 的半径( ) A 、5㎝ B、 11 ㎝ C、3㎝ D、5㎝或 11 ㎝ 13 .如图所示,两个等圆 ⊙ O 和 ⊙ O 1 相切,过 O 作 ⊙ O 1 的两条切线 OA 、 OB,A 、B为切点,则∠ AOB= __________ 14. 如图, B 是线段 AC 上的一点,且 AB : AC=2 : 5 ,分别以 AB 、 AC 为直径画圆,则小圆的面积与大圆的面积之比为 _______ . 15.已知 ∠ AOB=30° , C 是射线 OB 上的一点,且 OC=4 ,若以 C 为圆心, r 为半径的圆与射线 OA 有两个不同的交点,则 r 的取值范围是 _______ 16.(益阳市2010年中考题12).如图,分别以A、B为圆心,线段AB的长为半径的两个圆相交于C、D两点,则∠CAD的度数为 .17. (上海)已知圆O1、圆O2的半径不相等,圆O1的半径长为3,若圆O2上的点A满足AO1 = 3,则圆O1与圆O2的位置关系是( )A.相交或相切 B.相切或相离 C.相交或内含 D.相切或内含18.(2010年济宁市)已知⊙O1与⊙O2相切,⊙O1的半径为3 cm,⊙O2的半径为2 cm,则O1O2的长是( )A.1 cm B.5 cm C.1 cm或5 cm D.0.5cm或2.5cm19(2009年重庆市江津区)如图,在10×6的网格图中(每个小正方形的边长均为1个单位长)。⊙A半径为2,⊙B半径为1,需使⊙A与静止的⊙B相切,那么⊙A由图示的位置向左平移 个单位长.
拓展延伸: 学习感悟
如图,轮椅车的大小两车轮(在同一平面上)与地面的触点 间距离为 80cm ,两车轮的直径分别为 136cm , 16cm ,则此两车轮的圆心相距 cm . 2.一个圆环的面积为9 ,大圆的弦 AB 切小圆于点 C ,则弦AB=_____。 (第 2 题图)
反思: 学习感悟
B
A
O
x
y
B
C
A
A
B
C
O
x
第题图
y
O
1
A
C
B
1
x
y
第10题图
A
B
P
O
H
H
A
B
C
P
Q
O
(第题)
(第1题图)
A
B
同课章节目录
