24.1-24.4圆的性质导学案
文档属性
| 名称 | 24.1-24.4圆的性质导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 436.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-19 21:18:24 | ||
图片预览




文档简介
课题:24.1 圆(第1课时)
教与学目标: 探索圆的两种定义,理解并掌握弧、弦、优弧、劣弧、半圆等基本概念,能够从图形中识别
重点: 圆的两种定义的探索,能够解释一些生活问题
难点: 圆的运动式定义方法
自主探究: 学习感悟
(一)学生预习 教师导学:1.举例说出生活中的圆。2你是怎样画圆的?你能讲出形成圆的方法有多少种吗?自学课本P78---P79思考下列问题:3.分别用不同的方法作圆,标明圆心、半径,体会圆的形成过程。如图2,观察下列画圆的过程,你能由此说出圆的形成过程吗?⑴从圆的形成过程,我们可以得出: 在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的______叫做圆.固定的端点O叫做______,线段OA叫做_______. 以点O为圆心的圆,记作“ ______”,读作“______”.⑵、确定圆有两个要素:一是________,二是__________;____________确定圆的位置,__________确定圆的大小⑶尝试作⊙O1、⊙O2半径分别为2㎝和3㎝,感受圆的形成。你能讲出形成圆的方法有多少种?(二)学生探究 教师引领4.小组学习讨论下面的两个问题: 问题1:圆上各点到定点(圆心O)的距离有什么规律? 问题2:到定点的距离等于定长的点又有什么特点?(1)圆上各点到定点(圆心O)的距离__________________________(半径r);(2)到定点的距离等于定长的点__________________________.因此,我们可以得到圆的新定义:圆心为O,半径为r的圆可以看成是_________________________________________________________的点组成的图形.4.☆圆的两种(动态/静态)定义是什么?⑴. (动态)圆: ;圆心: ;半径: ;圆的表示方法:以点O为圆心的圆,记作“⊙O”,读作“圆O⑵. (静态)圆: 5.为什么车轮是圆的?6.弄清圆的有关概念?怎样用数学符号表示?讨论圆中相关元素的定义.如图3,你能说出弦、直径、弧、半圆的定义吗?并结合图形具体说明.弦: ;直径: ;弧: ;弧的表示方法: ;半圆: ; 优弧: ;劣弧: ;等圆: ;等弧: ;同心圆: ; (三)学生归纳 教师提炼圆心决定圆的位置,而半径决定圆的大小,直径是圆中经过圆心的特殊的弦,是最长的弦,并且等于半径的2倍,但弦不一定是直径,过圆上一点和圆心的直径有且只有一条,半圆是特殊的弧,而弧不一定是半圆。“同圆”指的是同一个圆,“等圆”指的是两个圆的位置、大小关系。判定两个圆是否是等圆,常用的方法是看其半径是否相等,半径相等的两个圆是等圆。“等弧”是能够重合的两条弧,而长度相等的两条弧不一定是等弧。为什么车轮是圆的?把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
课堂展示: 学习感悟
(四)学生展示 教师激励1.如何在操场上画一个半径是5m的圆?请说明理由。2.已知:如图,四边形是矩形,对角线、交于点.求证:点、、、在以为圆心的圆上.
课堂检测: 学习感悟
1.如图所示,在⊙O中AB、CD为直径,请判断AD与BC的位置关系。2.下列说法正确的是 ①直径是弦 ②弦是直径 ③半径是弦 ④半圆是弧,但弧不一定是半圆 ⑤半径相等的两个半圆是等弧 ⑥长度相等的两条弧是等弧 ⑦等弧的长度相等3.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的直径是( )A.2.5cm或6.5cm B.2.5cm C.6.5cm D.5cm或13cm4.如图所示,________是直径,________是弦, _________是劣弧,_______________是优弧.5.如果a,d分别是同一个圆的弦和直径,则a,d的大小关系是__________________.6以O为圆心的圆可以画_________个圆,这些圆叫 _______________。 以2cm为半径的圆可以画________个圆,这些圆是________________。 7.你见过树木的年轮吗?从树木的年轮,可以清楚的看出树木生长的年龄,把树木的年轮看成是圆形的,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径平均每年增加多少?
拓展延伸:
.一财主有一块平行四边形的土地,地里有一个圆形池塘,财主立下遗嘱,要把这块土地平均分给他的两个儿子,中间的池塘也平分,但不知道怎么分,你能帮他吗
反思: 学习感悟
课题:24.1.2 垂直于弦的直径(第1课时)
教与学目标: 1. 探索圆的对称性,进而得到垂直于弦的直径所具有的性质。2. 能够利用垂直于弦的直径的性质解决相关实际问题。
重点: 垂直于弦的直径所具有的性质以及证明。
难点: 利用垂直于弦的直径的性质解决实际问题
自主探究: 学习感悟
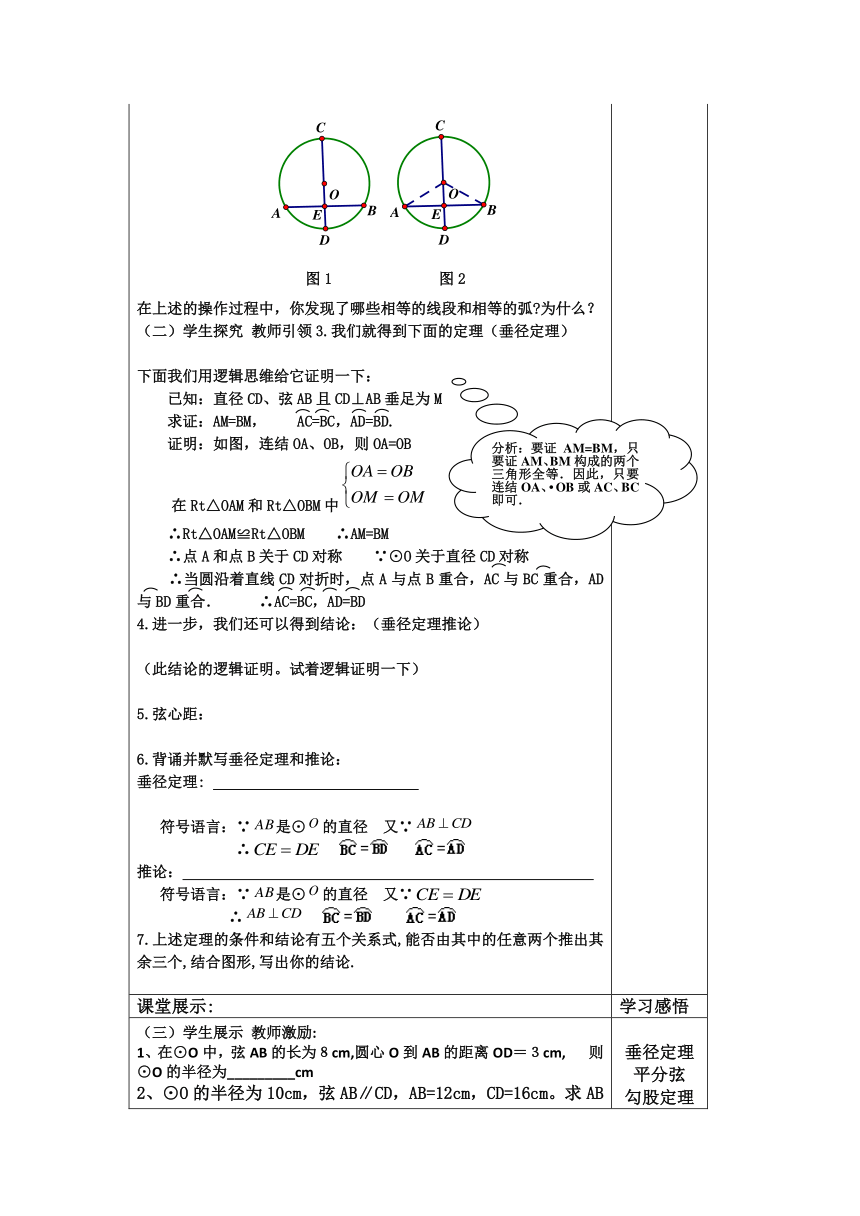
(一) 学生预习 教师导学:阅读课本P80---P81思考下列问题:1.用纸剪一个圆,沿着圆的任意一条直径对折,重复做几次,你发现了什么?由此你能得到什么结论?圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴? 2. 按下面的步骤做一做:第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合;第二步,得到一条折痕CD;第三步,在⊙O上任取一点A,过点A作CD折痕的垂线,得到新的折痕,其中点E是两条折痕的交点,即垂足;第四步,将纸打开,新的折痕与圆交于另一点B,如图1.图1 图2在上述的操作过程中,你发现了哪些相等的线段和相等的弧 为什么?(二)学生探究 教师引领3.我们就得到下面的定理(垂径定理)下面我们用逻辑思维给它证明一下: 已知:直径CD、弦AB且CD⊥AB垂足为M 求证:AM=BM, AC=BC,AD=BD. 证明:如图,连结OA、OB,则OA=OB在Rt△OAM和Rt△OBM中 ∴Rt△OAM≌Rt△OBM ∴AM=BM ∴点A和点B关于CD对称 ∵⊙O关于直径CD对称∴当圆沿着直线CD对折时,点A与点B重合,AC与BC重合,AD与BD重合. ∴AC=BC,AD=BD4.进一步,我们还可以得到结论:(垂径定理推论)(此结论的逻辑证明。试着逻辑证明一下)5.弦心距:6.背诵并默写垂径定理和推论:垂径定理: 符号语言:∵是⊙的直径 又∵ ∴ 推论: 符号语言:∵是⊙的直径 又∵∴ 7.上述定理的条件和结论有五个关系式,能否由其中的任意两个推出其余三个,结合图形,写出你的结论.
课堂展示: 学习感悟
学生展示 教师激励:1、在⊙O中,弦AB的长为8cm,圆心O到AB的距离OD=3cm, 则⊙O的半径为_________cm2、⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm。求AB与CD的距离 3.如图,在⊙中, 、为互相垂直且相等的两条弦,于, 于. 求证:四边形为正方形.4.如图所示,两个同心圆,大圆的弦交小圆于、.求证: (四)学生归纳 教师提炼在圆中,解决有关弦的问题时常常需要作“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作一条与弦垂直的线段即可.这样把垂径定理和勾股定理结合起来,容易得到圆的半径R,圆心到弦的距离d ,弦长a之间的关系式 这是一种重要的添加辅助线的方法 . 垂径定理平分弦勾股定理来计算半径连接弦心距,弦长一半是关键
课堂检测: 学习感悟
学生达标 教师测评:1.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为________;最长弦长_ . 2.如图,已知⊙O的半径为5mm,弦AB=8mm,则圆心O到AB的距离是( ) A.1mm B.2mmm C.3mm D.4mm3.如图,OE、OF分别为⊙O的弦AB、CD的弦心距,如果OE=OF,那么_______(只需写一个正确的结论) (2题图) (3题图) (4题图)4.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,则CD长为 .5.如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4,则∠AED=____ (7题图)6.如图,AB为⊙O直径,E是BC中点,OE交BC于点D,BD=3,AB =10,则AC=____.7.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD =3:5.求AB的长8.如图,在⊙O中,直径CD垂直弦AB于点E,连接OB,CB,已知⊙O的半径为2,AB=,则∠BCD=________度.9.如图,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中,错误的是( ).A.CE=DE B. C.∠BAC=∠BAD D.AC>AD10.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是( )A.4 B.6 C.7 D.8 9 10 1111.如图,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是( )A.AB⊥CD B.∠AOB=4∠ACD C. D.PO=PD
反思: 学习感悟
课题:24.1.2 垂直于弦的直径(第2课时)
教与学目标: 能够利用垂直于弦的直径的性质解决相关实际问题
重点: 能够利用垂直于弦的直径的性质解决相关实际问题
难点: 能够利用垂直于弦的直径的性质解决相关实际问题
自主探究: 学习感悟
(一)学生预习 教师导学: 1题 2题如图CD为⊙O的直径,CD⊥AB于E,,则 、 ,, 。如图CD为⊙O的直径,AE=BE,,则 、 ,, 。1.如图,CD是⊙O的弦,直径AB过垂直于CD欲点M,若∠BOC=40°,则∠ABD= A.40° B.60° C.70° D.80°2、如图,△ ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤,正确结论的个数是 A、2 B、3 C、4 D、5 3.结合图形默写垂径定理,写出数学符号语言4.跨度拱高6.弦心距: (二) 学生探究 教师引领.你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4,拱高(弧的中点到弦的距离)为7.2,请你求出赵州桥主桥拱的半径。(三)学生归纳教师提练.在圆中,解决有关弦的问题时常常需要作“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作一条与弦垂直的线段即可.这样把垂径定理和勾股定理结合起来,容易得到圆的半径R,圆心到弦的距离d ,弦长a之间的关系式 这是一种重要的添加辅助线的方法 .
课堂展示: 学习感悟
(四)学生展示,教师激励1.如图,某花园小区一圆形管道破裂,修理工准备更换一段新管道,现在量得污水水面宽度为80cm,水面到管道顶部距离为20cm,则修理工应准备内直径是 cm的管道.2..在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm截面如图,油的最大深度 mm3.如图,一条公路的转弯处是一段圆弧(即图中,点O是的圆心,其中CD=600m,E为上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.解:
课堂检测: 学习感悟
9.如图,M是⊙O中弦CD的中点,EM经过点O,若CD=4,EM=6,求⊙O的半径.2如图,所在圆的圆心是点O,过O作OC⊥AB于点D,若CD=4 m,弦AB=16 m,求此圆的半径.5.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P 320千米处. (1) 说明本次台风会影响B市;2)求这次台风影响B市的时间.(
拓展延伸: 学习感悟
1.某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7.2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2.4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?2..有一石拱桥的桥拱是圆弧形,如图所示,正常水位下水面宽AB=60m,水面到拱顶距离CD=18m,当洪水泛滥时,水面宽MN=32m时是否需要采取紧急措施?请说明理由.(当水面距拱顶3米以内时需采取紧急措施).
反思: 学习感悟
课题:24.1.3圆弧弦圆心角
教与学目标: 1. 了解圆心角的概念:掌握在同圆或等圆中,圆心角、弦、弧中有一个量的两个相等就可以推出其它两个量的相对应的两个值就相等,及其它们在解题中的应用。2. 通过复习旋转的知识,产生圆心角的概念,然后用圆心角和旋转的知识探索在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等,最后应用它解决一些具体问题
重点: 探索圆心角、弧、弦之间关系定理并利用其解决相关问题。
难点: 圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的理解及定理的证明
自主探究: 学习感悟
自学课本P82---P83思考下列问题:1.举例说明什么是圆心角?如图所示,∠AOB的顶点在 ,像这样 的角叫做圆心角2、如图所示的⊙O中,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置,你能发现哪些等量关系?为什么?因此,在同一个圆中,相等的圆心角所对的_____相等,所对的 相等.3、 在⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A′O′B′得到如图2,滚动一个圆,使O与O′重合,固定圆心,将其中的一个圆旋转一个角度,使得OA与O′A′重合.你能发现哪些等量关系?在等圆中,相等的圆心角是否也有所对的弧相等,所对的弦相等吗?因此,我们可以得到下面的定理:______ _________________。4.在圆心角的性质中定理中,为什么要说“同圆或等圆”?能不能去掉?5.由探究得到的定理及结论是什么?在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦 。在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角 相等,所对的弦 也相等.在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 相等,所对的 优弧 也相等.所对的劣弧 也相等.
课堂展示: 学习感悟
1.如图,在⊙中,,.求证:2.如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF. (1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?(2)如果OE=OF,那么AB与CD的大小有什么关系?劣弧AB与劣弧CD的大小有什么关系?为什么?∠AOB与∠COD呢?
课堂检测: 学习感悟
1.如果两个圆心角相等,那么( ) A.这两个圆心角所对的弦相等;B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等;D.以上说法都不对2.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD关系是( ) A.=2 B.> C.<2 D.不能确定 .3.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________.4.如图2,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.5.如图,、是⊙O的两条弦.⑴如果,则有 , .⑵如果,则有 , .⑶如果,则有 , .⑷如果,于,于,则与相等吗?为什么?6.如图,⊙中,如果=2,那么( ).A. B. C. D. 4 5 67.如图,AB是⊙O的直径,C、D是弧BE的两个等分点,∠COD=35°,求∠AOE的度数.
拓展延伸: 学习感悟
如图1和图2,MN是⊙O的直径,弦AB、CD相交于MN上的一点P,∠APM=∠CPM. (1)由以上条件,你认为AB和CD大小关系是什么,请说明理由.(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由. ( http: / / ) (图1) (图2)
反思: 学习感悟
课题:24.1.4圆周角(第1课时)
教与学目标: 1. 了解圆周角的概念。2. 理解圆周角的定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。3.理解圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
重点: 探索圆周角与圆心角的关系,发现圆周角的性质和直径所对圆周角的特征
难点: 发现并论证圆周角定理
自主探究: 学习感悟
自学教材,思考下列问题:如图,点A在⊙O外,点B1 、B2 、B3在⊙O上,点C在⊙O内,度量∠A、∠B1 、∠B2 、∠B3 、∠C的大小,你能发现什么? ∠B1 、∠B2 、∠B3有什么共同的特征?_____________。归纳得出结论,顶点在_______,并且两边_______________________的角叫做圆周角。 2.在下面空里作一个圆,在同一弧上作一些圆心角及圆周角。通过圆周角的概念和度量的方法回答下面的问题.一个弧上所对的圆周角的个数有多少个?有几种情况?(2)同弧所对的圆周角的度数是否发生变化?(3)同弧上的圆周角与圆心角有什么关系?3.默写圆周角定理及推论并证明。圆周角定理4.能去掉“同圆或等圆”吗?若把“同弧或等弧”改成“同弦或等弦”性质成立吗?5思考?在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?
课堂展示: 学习感悟
1.如图,点A,B,C,D在同一圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些角是相等的角?2’如图,A\B是⊙O上的四点,∠AOB=120°C是弧AB的中点,求证四边形OACB为菱形.
课堂检测: 学习感悟
1.如图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ).A.140° B.110° C.120° D.130°(1)(2) ( http: / / ) (3)2.如图,⊙O是△ABC的外接圆,∠OCB=40°则∠A的度数等于( )A. 60° B. 50° C. 40° D. 30°3如图,OB是⊙O的半径,点C、D在⊙O上,∠DCB=27°,则∠OBD= 度。4. AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( )A.100° B.110° C.120° D.130°5.半径为2a的⊙O中,弦AB的长为2a,则弦AB所对的圆周角的度数是________.6.如图,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2= 。
拓展延伸: 学习感悟
1.如图,点A、B、C、D在⊙O上,∠ADC=∠BDC=60°.判断△ABC的形状,并说明理由. )若BC=4cm,求⊙O的面积.2.(开放题)AB是⊙O的直径,AC、AD是⊙O的两弦,已知AB=16,AC=8,AD=8,求∠DAC的度数.
反思: 学习感悟
课题:24.1圆周角(第2课时)
教与学目标: 1.掌握直径(或半圆)所对的圆周角是直角及90°的圆周角所对的弦是直径。并能运用解决问题. 2.经历圆周角性质的过程,培养学生分析问题和解决问题的能力. 3.激发学生探索新知的兴趣,培养刻苦学习的精神,进一步体会数学源于生活并用于生活.
重点: 圆周角的性质
难点: 圆周角性质的应用
自主探究: 学习感悟
如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?为什么? (意图:引导学生探究问题的解法)2.如图,在⊙O中,圆周角∠BAC=90°,弦BC经过圆心吗?为什么?3.归纳自己总结的结论: (1) (2) 注意:(1)这里所对的角、90°的角必须是圆周角; (2)直径所对的圆周角是直角,在圆的有关问题中经常遇到,同学们要高度重视.圆周角定理推论: 注意:这里所对的角、90°的角必须是圆周角;4、如图,四边形的四个顶点都在⊙O上.⑴如图1,猜想四边形的对角的关系,并说明理由.⑵如图2,⑴中的结论是否成立?并说明理由.圆内接多边形的定义: 5、如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。∠A与∠DCB的外角有什么关系 圆周角定理推论:圆的内接四边形的对角 ,并且任何一个外角都等于 例1、如又图⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长。
课堂展示: 学习感悟
1..求证:如果直角三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。(提示:作出以这条边为直径的圆)2、如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?
课堂检测: 学习感悟
1、如图,四边形ABCD内接于⊙O,则= 。2.已知AB是⊙O的直径,AE是弦,C是的中点,CD⊥AB于D,交AE于F,CB交AE于G.求证:CF=FG.
4、3.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数.4.、如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长.5.如图,AB是⊙O的直径,C是的中点,CE⊥AB于 E,BD交CE于点F.(1)求证:CF﹦BF;(2)若CD ﹦6, AC ﹦8,则⊙O的半径为 , CE的长是 .6.如图,,点C在上,且点C不与A、B重合,则的度数为( )A. B.或 C. D. 或7.如图,已知AB为⊙O的直径,∠CAB=30°,则∠D= .8.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD =105°,则∠DCE的大小是
拓展延伸: 学习感悟
(2011浙江省,5,3分)如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )A. 12个单位 B. 10个单位 C.4个单位 D. 15个单位
反思: 学习感悟
构造直径所对的圆周角是直角是圆中常见辅助线作法.
图2
图3
_
B
_
A
_
C
_
O
分析:要证AM=BM,只要证AM、BM构成的两个三角形全等.因此,只要连结OA、OB或AC、BC即可.
A
B
O
D
E
C
(5题图)
6题图
(第8题)
(4题图)
(2)
O
D
B
C
A
C
B
D
(第5题图)
E
F
O
1
2
A
B
C
D
E
教与学目标: 探索圆的两种定义,理解并掌握弧、弦、优弧、劣弧、半圆等基本概念,能够从图形中识别
重点: 圆的两种定义的探索,能够解释一些生活问题
难点: 圆的运动式定义方法
自主探究: 学习感悟
(一)学生预习 教师导学:1.举例说出生活中的圆。2你是怎样画圆的?你能讲出形成圆的方法有多少种吗?自学课本P78---P79思考下列问题:3.分别用不同的方法作圆,标明圆心、半径,体会圆的形成过程。如图2,观察下列画圆的过程,你能由此说出圆的形成过程吗?⑴从圆的形成过程,我们可以得出: 在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的______叫做圆.固定的端点O叫做______,线段OA叫做_______. 以点O为圆心的圆,记作“ ______”,读作“______”.⑵、确定圆有两个要素:一是________,二是__________;____________确定圆的位置,__________确定圆的大小⑶尝试作⊙O1、⊙O2半径分别为2㎝和3㎝,感受圆的形成。你能讲出形成圆的方法有多少种?(二)学生探究 教师引领4.小组学习讨论下面的两个问题: 问题1:圆上各点到定点(圆心O)的距离有什么规律? 问题2:到定点的距离等于定长的点又有什么特点?(1)圆上各点到定点(圆心O)的距离__________________________(半径r);(2)到定点的距离等于定长的点__________________________.因此,我们可以得到圆的新定义:圆心为O,半径为r的圆可以看成是_________________________________________________________的点组成的图形.4.☆圆的两种(动态/静态)定义是什么?⑴. (动态)圆: ;圆心: ;半径: ;圆的表示方法:以点O为圆心的圆,记作“⊙O”,读作“圆O⑵. (静态)圆: 5.为什么车轮是圆的?6.弄清圆的有关概念?怎样用数学符号表示?讨论圆中相关元素的定义.如图3,你能说出弦、直径、弧、半圆的定义吗?并结合图形具体说明.弦: ;直径: ;弧: ;弧的表示方法: ;半圆: ; 优弧: ;劣弧: ;等圆: ;等弧: ;同心圆: ; (三)学生归纳 教师提炼圆心决定圆的位置,而半径决定圆的大小,直径是圆中经过圆心的特殊的弦,是最长的弦,并且等于半径的2倍,但弦不一定是直径,过圆上一点和圆心的直径有且只有一条,半圆是特殊的弧,而弧不一定是半圆。“同圆”指的是同一个圆,“等圆”指的是两个圆的位置、大小关系。判定两个圆是否是等圆,常用的方法是看其半径是否相等,半径相等的两个圆是等圆。“等弧”是能够重合的两条弧,而长度相等的两条弧不一定是等弧。为什么车轮是圆的?把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
课堂展示: 学习感悟
(四)学生展示 教师激励1.如何在操场上画一个半径是5m的圆?请说明理由。2.已知:如图,四边形是矩形,对角线、交于点.求证:点、、、在以为圆心的圆上.
课堂检测: 学习感悟
1.如图所示,在⊙O中AB、CD为直径,请判断AD与BC的位置关系。2.下列说法正确的是 ①直径是弦 ②弦是直径 ③半径是弦 ④半圆是弧,但弧不一定是半圆 ⑤半径相等的两个半圆是等弧 ⑥长度相等的两条弧是等弧 ⑦等弧的长度相等3.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的直径是( )A.2.5cm或6.5cm B.2.5cm C.6.5cm D.5cm或13cm4.如图所示,________是直径,________是弦, _________是劣弧,_______________是优弧.5.如果a,d分别是同一个圆的弦和直径,则a,d的大小关系是__________________.6以O为圆心的圆可以画_________个圆,这些圆叫 _______________。 以2cm为半径的圆可以画________个圆,这些圆是________________。 7.你见过树木的年轮吗?从树木的年轮,可以清楚的看出树木生长的年龄,把树木的年轮看成是圆形的,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径平均每年增加多少?
拓展延伸:
.一财主有一块平行四边形的土地,地里有一个圆形池塘,财主立下遗嘱,要把这块土地平均分给他的两个儿子,中间的池塘也平分,但不知道怎么分,你能帮他吗
反思: 学习感悟
课题:24.1.2 垂直于弦的直径(第1课时)
教与学目标: 1. 探索圆的对称性,进而得到垂直于弦的直径所具有的性质。2. 能够利用垂直于弦的直径的性质解决相关实际问题。
重点: 垂直于弦的直径所具有的性质以及证明。
难点: 利用垂直于弦的直径的性质解决实际问题
自主探究: 学习感悟
(一) 学生预习 教师导学:阅读课本P80---P81思考下列问题:1.用纸剪一个圆,沿着圆的任意一条直径对折,重复做几次,你发现了什么?由此你能得到什么结论?圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴? 2. 按下面的步骤做一做:第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合;第二步,得到一条折痕CD;第三步,在⊙O上任取一点A,过点A作CD折痕的垂线,得到新的折痕,其中点E是两条折痕的交点,即垂足;第四步,将纸打开,新的折痕与圆交于另一点B,如图1.图1 图2在上述的操作过程中,你发现了哪些相等的线段和相等的弧 为什么?(二)学生探究 教师引领3.我们就得到下面的定理(垂径定理)下面我们用逻辑思维给它证明一下: 已知:直径CD、弦AB且CD⊥AB垂足为M 求证:AM=BM, AC=BC,AD=BD. 证明:如图,连结OA、OB,则OA=OB在Rt△OAM和Rt△OBM中 ∴Rt△OAM≌Rt△OBM ∴AM=BM ∴点A和点B关于CD对称 ∵⊙O关于直径CD对称∴当圆沿着直线CD对折时,点A与点B重合,AC与BC重合,AD与BD重合. ∴AC=BC,AD=BD4.进一步,我们还可以得到结论:(垂径定理推论)(此结论的逻辑证明。试着逻辑证明一下)5.弦心距:6.背诵并默写垂径定理和推论:垂径定理: 符号语言:∵是⊙的直径 又∵ ∴ 推论: 符号语言:∵是⊙的直径 又∵∴ 7.上述定理的条件和结论有五个关系式,能否由其中的任意两个推出其余三个,结合图形,写出你的结论.
课堂展示: 学习感悟
学生展示 教师激励:1、在⊙O中,弦AB的长为8cm,圆心O到AB的距离OD=3cm, 则⊙O的半径为_________cm2、⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm。求AB与CD的距离 3.如图,在⊙中, 、为互相垂直且相等的两条弦,于, 于. 求证:四边形为正方形.4.如图所示,两个同心圆,大圆的弦交小圆于、.求证: (四)学生归纳 教师提炼在圆中,解决有关弦的问题时常常需要作“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作一条与弦垂直的线段即可.这样把垂径定理和勾股定理结合起来,容易得到圆的半径R,圆心到弦的距离d ,弦长a之间的关系式 这是一种重要的添加辅助线的方法 . 垂径定理平分弦勾股定理来计算半径连接弦心距,弦长一半是关键
课堂检测: 学习感悟
学生达标 教师测评:1.P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为________;最长弦长_ . 2.如图,已知⊙O的半径为5mm,弦AB=8mm,则圆心O到AB的距离是( ) A.1mm B.2mmm C.3mm D.4mm3.如图,OE、OF分别为⊙O的弦AB、CD的弦心距,如果OE=OF,那么_______(只需写一个正确的结论) (2题图) (3题图) (4题图)4.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,则CD长为 .5.如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4,则∠AED=____ (7题图)6.如图,AB为⊙O直径,E是BC中点,OE交BC于点D,BD=3,AB =10,则AC=____.7.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD =3:5.求AB的长8.如图,在⊙O中,直径CD垂直弦AB于点E,连接OB,CB,已知⊙O的半径为2,AB=,则∠BCD=________度.9.如图,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中,错误的是( ).A.CE=DE B. C.∠BAC=∠BAD D.AC>AD10.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是( )A.4 B.6 C.7 D.8 9 10 1111.如图,在⊙O中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是( )A.AB⊥CD B.∠AOB=4∠ACD C. D.PO=PD
反思: 学习感悟
课题:24.1.2 垂直于弦的直径(第2课时)
教与学目标: 能够利用垂直于弦的直径的性质解决相关实际问题
重点: 能够利用垂直于弦的直径的性质解决相关实际问题
难点: 能够利用垂直于弦的直径的性质解决相关实际问题
自主探究: 学习感悟
(一)学生预习 教师导学: 1题 2题如图CD为⊙O的直径,CD⊥AB于E,,则 、 ,, 。如图CD为⊙O的直径,AE=BE,,则 、 ,, 。1.如图,CD是⊙O的弦,直径AB过垂直于CD欲点M,若∠BOC=40°,则∠ABD= A.40° B.60° C.70° D.80°2、如图,△ ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤,正确结论的个数是 A、2 B、3 C、4 D、5 3.结合图形默写垂径定理,写出数学符号语言4.跨度拱高6.弦心距: (二) 学生探究 教师引领.你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4,拱高(弧的中点到弦的距离)为7.2,请你求出赵州桥主桥拱的半径。(三)学生归纳教师提练.在圆中,解决有关弦的问题时常常需要作“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作一条与弦垂直的线段即可.这样把垂径定理和勾股定理结合起来,容易得到圆的半径R,圆心到弦的距离d ,弦长a之间的关系式 这是一种重要的添加辅助线的方法 .
课堂展示: 学习感悟
(四)学生展示,教师激励1.如图,某花园小区一圆形管道破裂,修理工准备更换一段新管道,现在量得污水水面宽度为80cm,水面到管道顶部距离为20cm,则修理工应准备内直径是 cm的管道.2..在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm截面如图,油的最大深度 mm3.如图,一条公路的转弯处是一段圆弧(即图中,点O是的圆心,其中CD=600m,E为上一点,且OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.解:
课堂检测: 学习感悟
9.如图,M是⊙O中弦CD的中点,EM经过点O,若CD=4,EM=6,求⊙O的半径.2如图,所在圆的圆心是点O,过O作OC⊥AB于点D,若CD=4 m,弦AB=16 m,求此圆的半径.5.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P 320千米处. (1) 说明本次台风会影响B市;2)求这次台风影响B市的时间.(
拓展延伸: 学习感悟
1.某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7.2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2.4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?2..有一石拱桥的桥拱是圆弧形,如图所示,正常水位下水面宽AB=60m,水面到拱顶距离CD=18m,当洪水泛滥时,水面宽MN=32m时是否需要采取紧急措施?请说明理由.(当水面距拱顶3米以内时需采取紧急措施).
反思: 学习感悟
课题:24.1.3圆弧弦圆心角
教与学目标: 1. 了解圆心角的概念:掌握在同圆或等圆中,圆心角、弦、弧中有一个量的两个相等就可以推出其它两个量的相对应的两个值就相等,及其它们在解题中的应用。2. 通过复习旋转的知识,产生圆心角的概念,然后用圆心角和旋转的知识探索在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等,最后应用它解决一些具体问题
重点: 探索圆心角、弧、弦之间关系定理并利用其解决相关问题。
难点: 圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的理解及定理的证明
自主探究: 学习感悟
自学课本P82---P83思考下列问题:1.举例说明什么是圆心角?如图所示,∠AOB的顶点在 ,像这样 的角叫做圆心角2、如图所示的⊙O中,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置,你能发现哪些等量关系?为什么?因此,在同一个圆中,相等的圆心角所对的_____相等,所对的 相等.3、 在⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A′O′B′得到如图2,滚动一个圆,使O与O′重合,固定圆心,将其中的一个圆旋转一个角度,使得OA与O′A′重合.你能发现哪些等量关系?在等圆中,相等的圆心角是否也有所对的弧相等,所对的弦相等吗?因此,我们可以得到下面的定理:______ _________________。4.在圆心角的性质中定理中,为什么要说“同圆或等圆”?能不能去掉?5.由探究得到的定理及结论是什么?在同圆或等圆中,相等的圆心角所对的弧 ,所对的弦 。在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角 相等,所对的弦 也相等.在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 相等,所对的 优弧 也相等.所对的劣弧 也相等.
课堂展示: 学习感悟
1.如图,在⊙中,,.求证:2.如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF. (1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?(2)如果OE=OF,那么AB与CD的大小有什么关系?劣弧AB与劣弧CD的大小有什么关系?为什么?∠AOB与∠COD呢?
课堂检测: 学习感悟
1.如果两个圆心角相等,那么( ) A.这两个圆心角所对的弦相等;B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等;D.以上说法都不对2.在同圆中,圆心角∠AOB=2∠COD,则两条弧AB与CD关系是( ) A.=2 B.> C.<2 D.不能确定 .3.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________.4.如图2,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.5.如图,、是⊙O的两条弦.⑴如果,则有 , .⑵如果,则有 , .⑶如果,则有 , .⑷如果,于,于,则与相等吗?为什么?6.如图,⊙中,如果=2,那么( ).A. B. C. D. 4 5 67.如图,AB是⊙O的直径,C、D是弧BE的两个等分点,∠COD=35°,求∠AOE的度数.
拓展延伸: 学习感悟
如图1和图2,MN是⊙O的直径,弦AB、CD相交于MN上的一点P,∠APM=∠CPM. (1)由以上条件,你认为AB和CD大小关系是什么,请说明理由.(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由. ( http: / / ) (图1) (图2)
反思: 学习感悟
课题:24.1.4圆周角(第1课时)
教与学目标: 1. 了解圆周角的概念。2. 理解圆周角的定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。3.理解圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
重点: 探索圆周角与圆心角的关系,发现圆周角的性质和直径所对圆周角的特征
难点: 发现并论证圆周角定理
自主探究: 学习感悟
自学教材,思考下列问题:如图,点A在⊙O外,点B1 、B2 、B3在⊙O上,点C在⊙O内,度量∠A、∠B1 、∠B2 、∠B3 、∠C的大小,你能发现什么? ∠B1 、∠B2 、∠B3有什么共同的特征?_____________。归纳得出结论,顶点在_______,并且两边_______________________的角叫做圆周角。 2.在下面空里作一个圆,在同一弧上作一些圆心角及圆周角。通过圆周角的概念和度量的方法回答下面的问题.一个弧上所对的圆周角的个数有多少个?有几种情况?(2)同弧所对的圆周角的度数是否发生变化?(3)同弧上的圆周角与圆心角有什么关系?3.默写圆周角定理及推论并证明。圆周角定理4.能去掉“同圆或等圆”吗?若把“同弧或等弧”改成“同弦或等弦”性质成立吗?5思考?在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?
课堂展示: 学习感悟
1.如图,点A,B,C,D在同一圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些角是相等的角?2’如图,A\B是⊙O上的四点,∠AOB=120°C是弧AB的中点,求证四边形OACB为菱形.
课堂检测: 学习感悟
1.如图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ).A.140° B.110° C.120° D.130°(1)(2) ( http: / / ) (3)2.如图,⊙O是△ABC的外接圆,∠OCB=40°则∠A的度数等于( )A. 60° B. 50° C. 40° D. 30°3如图,OB是⊙O的半径,点C、D在⊙O上,∠DCB=27°,则∠OBD= 度。4. AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( )A.100° B.110° C.120° D.130°5.半径为2a的⊙O中,弦AB的长为2a,则弦AB所对的圆周角的度数是________.6.如图,AB是⊙O的直径,C、D、E都是⊙O上的点,则∠1+∠2= 。
拓展延伸: 学习感悟
1.如图,点A、B、C、D在⊙O上,∠ADC=∠BDC=60°.判断△ABC的形状,并说明理由. )若BC=4cm,求⊙O的面积.2.(开放题)AB是⊙O的直径,AC、AD是⊙O的两弦,已知AB=16,AC=8,AD=8,求∠DAC的度数.
反思: 学习感悟
课题:24.1圆周角(第2课时)
教与学目标: 1.掌握直径(或半圆)所对的圆周角是直角及90°的圆周角所对的弦是直径。并能运用解决问题. 2.经历圆周角性质的过程,培养学生分析问题和解决问题的能力. 3.激发学生探索新知的兴趣,培养刻苦学习的精神,进一步体会数学源于生活并用于生活.
重点: 圆周角的性质
难点: 圆周角性质的应用
自主探究: 学习感悟
如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?为什么? (意图:引导学生探究问题的解法)2.如图,在⊙O中,圆周角∠BAC=90°,弦BC经过圆心吗?为什么?3.归纳自己总结的结论: (1) (2) 注意:(1)这里所对的角、90°的角必须是圆周角; (2)直径所对的圆周角是直角,在圆的有关问题中经常遇到,同学们要高度重视.圆周角定理推论: 注意:这里所对的角、90°的角必须是圆周角;4、如图,四边形的四个顶点都在⊙O上.⑴如图1,猜想四边形的对角的关系,并说明理由.⑵如图2,⑴中的结论是否成立?并说明理由.圆内接多边形的定义: 5、如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。∠A与∠DCB的外角有什么关系 圆周角定理推论:圆的内接四边形的对角 ,并且任何一个外角都等于 例1、如又图⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长。
课堂展示: 学习感悟
1..求证:如果直角三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。(提示:作出以这条边为直径的圆)2、如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?
课堂检测: 学习感悟
1、如图,四边形ABCD内接于⊙O,则= 。2.已知AB是⊙O的直径,AE是弦,C是的中点,CD⊥AB于D,交AE于F,CB交AE于G.求证:CF=FG.
4、3.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数.4.、如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长.5.如图,AB是⊙O的直径,C是的中点,CE⊥AB于 E,BD交CE于点F.(1)求证:CF﹦BF;(2)若CD ﹦6, AC ﹦8,则⊙O的半径为 , CE的长是 .6.如图,,点C在上,且点C不与A、B重合,则的度数为( )A. B.或 C. D. 或7.如图,已知AB为⊙O的直径,∠CAB=30°,则∠D= .8.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD =105°,则∠DCE的大小是
拓展延伸: 学习感悟
(2011浙江省,5,3分)如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )A. 12个单位 B. 10个单位 C.4个单位 D. 15个单位
反思: 学习感悟
构造直径所对的圆周角是直角是圆中常见辅助线作法.
图2
图3
_
B
_
A
_
C
_
O
分析:要证AM=BM,只要证AM、BM构成的两个三角形全等.因此,只要连结OA、OB或AC、BC即可.
A
B
O
D
E
C
(5题图)
6题图
(第8题)
(4题图)
(2)
O
D
B
C
A
C
B
D
(第5题图)
E
F
O
1
2
A
B
C
D
E
同课章节目录
