甘肃省张掖中学2013届高三上学期第二次月考数学文试题
文档属性
| 名称 | 甘肃省张掖中学2013届高三上学期第二次月考数学文试题 |  | |
| 格式 | zip | ||
| 文件大小 | 159.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-19 22:04:27 | ||
图片预览


文档简介
甘肃省张掖中学2013届高三上学期第二次月考数学(文)试卷
第Ⅰ卷
一、选择题:(本大题共12小题.每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,则
A . B . C . D.
设为定义在上的奇函数,当时,,则
A.-1 B.-4 C.1 D.4
3.函数的定义域是
A. B. C. D.
4.函数y=x3-3x的极大值为m,极小值为n,则m+n为
A.0 B.1 C.2 D.4
5.命题“对任意的”的否定是
A.不存在 B.存在
C.存在 D. 对任意的
6.函数在区间内的零点个数是
A.0 B.1 C.2 D.3
7.下列函数中,既是奇函数又是增函数的为
A. B. C. D.
8.设,,,则下列关系中正确的是
A. B. C. D.
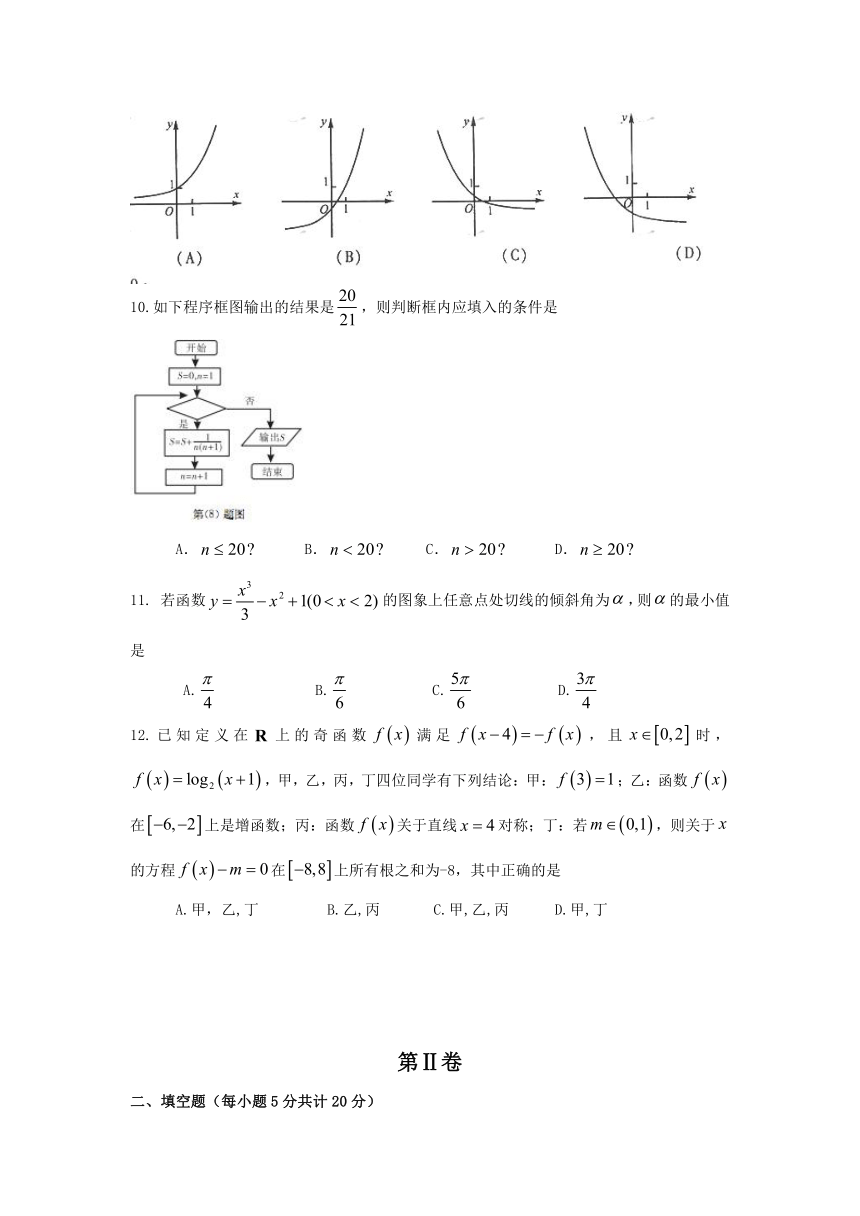
9.函数的图象可能是
10.如下程序框图输出的结果是,则判断框内应填入的条件是
A. B. C. D.
11. 若函数的图象上任意点处切线的倾斜角为,则的最小值是
A. B. C. D.
12.已知定义在上的奇函数满足,且时,,甲,乙,丙,丁四位同学有下列结论:甲:;乙:函数在上是增函数;丙:函数关于直线对称;丁:若,则关于的方程在上所有根之和为-8,其中正确的是
A.甲,乙,丁 B.乙,丙 C.甲,乙,丙 D.甲,丁
第Ⅱ卷
二、填空题(每小题5分共计20分)
13.已知幂函数的图象过(4,2)点,则= .
14.等比数列{an}的前n项和为Sn,若,则公比q=_______.
15.在△ABC中,AB=7,BC=5,CA=6,则= .
16.设是定义在上的偶函数,对任意的,都有,且当时,,若关于的方程在区间内恰有三个不同实根,则实数的取值范围是 .
三、解答题(6个小题,共计70分)
17.(10分)已知集合A=,B=,
(1)当时,求;
(2)若,求实数的取值范围。
18.(本小题满分12分)
已知
(1)求的最小正周期及单调递减区间;
(2)当时,求的最大值和最小值。
19.(本小题满分12分)椭圆的离心率为,椭圆与直线相交于点P、Q,且.求椭圆的方程.
20.(本题12分)
袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)向袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
21. (本小题满分12分)
已知函数f(x)=x2+alnx.
(1)当a=-2时,求函数f(x)的单调区间和极值;
(2)若g(x)=f(x)+在[1,+∞)上是单调增函数,求实数a的取值范围.
22 .(本小题满分12分)
已知函数f(x)=ex-ax,其中a>0.
(1)若对一切x∈R,f(x)≥1恒成立,求a的取值集合;
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使f′(x0)=k成立.
甘肃省张掖中学2012--2013学年高三第二次月考
数学 (文科)答案
18.解:
19.解:
20.解:(1)标号为1,2,3的三张红色卡片分别记为A,B,C,标号为1,2的两张蓝色卡片分别记为D,E.从五张卡片中任取两张的所有可能的结果为:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E).共10种.
由于每一张卡片被取到的机会均等,因此这些基本事件的出现是等可能的.
从五张卡片中任取两张,这两张卡片颜色不同且它们的标号之和小于4的结果为:(A,D),(A,E),(B,D),共3种.
所以这两张卡片颜色不同且它们的标号之和小于4的概率为.
(2)记F为标号为0的绿色卡片,从六张卡片中任取两张的所有可能的结果为:
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种.
由于每一张卡片被取到的机会均等,因此这些基本事件的出现是等可能的.
从六张卡片中任取两张,这两张卡片颜色不同且它们的标号之和小于4的结果为:(A,D),(A,E),(B,D),(A,F),(B,F),(C,F),(D,F),(E,F),共8种.
所以这两张卡片颜色不同且它们的标号之和小于4的概率为.
21.解:(1)易知函数f(x)的定义域为(0,+∞).
当a=-2时,f(x)=x2-2lnx,f′(x)=2x-=.
当x变化时,f′(x)和f(x)的变化情况如下表:
x (0,1) 1 (1,+∞)
f′(x) - 0 +
f(x) 递减 极小值 递增
由上表可知,函数f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞),极小值是f(1)=1.
(2)由g(x)=x2+alnx+,得g′(x)=2x+-.
若函数g(x)为[1,+∞)上的单调增函数,则g′(x)≥0在[1,+∞)上恒成立,即不等式2x-+≥0在[1,+∞)上恒成立.也即a≥-2x2在[1,+∞)上恒成立.
令φ(x)=-2x2,则φ′(x)=--4x.
当x∈[1,+∞)时,φ′(x)=--4x<0,
∴φ(x)=-2x2在[1,+∞)上为减函数,
∴φ(x)max=φ(1)=0.
∴a≥0,即a的取值范围为[0,+∞).
22.解:(1)f′(x)=ex-a.令f′(x)=0得x=lna.
当x<lna时,f′(x)<0,f(x)单调递减;当x>lna时,f′(x)>0,f(x)单调递增.故当x=ln a时,f(x)取最小值f(lna)=a-alna.
于是对一切x∈R,f(x)≥1恒成立,当且仅当a-alna≥1. ①
令g(t)=t-tlnt,则g′(t)=-lnt.
当0<t<1时,g′(t)>0,g(t)单调递增;
当t>1时,g′(t)<0,g(t)单调递减.
故当t=1时,g(t)取最大值g(1)=1.因此,当且仅当a=1时,①式成立.
综上所述,a的取值集合为{1}.
(2)由题意知,k==-a.
令φ(x)=f′(x)-k=ex-,则
φ(x1)=- [-(x2-x1)-1],
φ(x2)= [-(x1-x2)-1].
令F(t)=et-t-1,则F′(t)=et-1.
当t<0时,F′(t)<0,F(t)单调递减;
当t>0时,F′(t)>0,F(t)单调递增.
故当t≠0时,F(t)>F(0)=0,即et-t-1>0.
从而-(x2-x1)-1>0,-(x1-x2)-1>0,又>0,>0,
所以φ(x1)<0,φ(x2)>0.
因为函数y=φ(x)在区间[x1,x2]上的图象是连续不断的一条曲线,所以存在x0∈(x1,x2),使φ(x0)=0,即f′(x0)=k成立.
第Ⅰ卷
一、选择题:(本大题共12小题.每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,则
A . B . C . D.
设为定义在上的奇函数,当时,,则
A.-1 B.-4 C.1 D.4
3.函数的定义域是
A. B. C. D.
4.函数y=x3-3x的极大值为m,极小值为n,则m+n为
A.0 B.1 C.2 D.4
5.命题“对任意的”的否定是
A.不存在 B.存在
C.存在 D. 对任意的
6.函数在区间内的零点个数是
A.0 B.1 C.2 D.3
7.下列函数中,既是奇函数又是增函数的为
A. B. C. D.
8.设,,,则下列关系中正确的是
A. B. C. D.
9.函数的图象可能是
10.如下程序框图输出的结果是,则判断框内应填入的条件是
A. B. C. D.
11. 若函数的图象上任意点处切线的倾斜角为,则的最小值是
A. B. C. D.
12.已知定义在上的奇函数满足,且时,,甲,乙,丙,丁四位同学有下列结论:甲:;乙:函数在上是增函数;丙:函数关于直线对称;丁:若,则关于的方程在上所有根之和为-8,其中正确的是
A.甲,乙,丁 B.乙,丙 C.甲,乙,丙 D.甲,丁
第Ⅱ卷
二、填空题(每小题5分共计20分)
13.已知幂函数的图象过(4,2)点,则= .
14.等比数列{an}的前n项和为Sn,若,则公比q=_______.
15.在△ABC中,AB=7,BC=5,CA=6,则= .
16.设是定义在上的偶函数,对任意的,都有,且当时,,若关于的方程在区间内恰有三个不同实根,则实数的取值范围是 .
三、解答题(6个小题,共计70分)
17.(10分)已知集合A=,B=,
(1)当时,求;
(2)若,求实数的取值范围。
18.(本小题满分12分)
已知
(1)求的最小正周期及单调递减区间;
(2)当时,求的最大值和最小值。
19.(本小题满分12分)椭圆的离心率为,椭圆与直线相交于点P、Q,且.求椭圆的方程.
20.(本题12分)
袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)向袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
21. (本小题满分12分)
已知函数f(x)=x2+alnx.
(1)当a=-2时,求函数f(x)的单调区间和极值;
(2)若g(x)=f(x)+在[1,+∞)上是单调增函数,求实数a的取值范围.
22 .(本小题满分12分)
已知函数f(x)=ex-ax,其中a>0.
(1)若对一切x∈R,f(x)≥1恒成立,求a的取值集合;
(2)在函数f(x)的图象上取定两点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使f′(x0)=k成立.
甘肃省张掖中学2012--2013学年高三第二次月考
数学 (文科)答案
18.解:
19.解:
20.解:(1)标号为1,2,3的三张红色卡片分别记为A,B,C,标号为1,2的两张蓝色卡片分别记为D,E.从五张卡片中任取两张的所有可能的结果为:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E).共10种.
由于每一张卡片被取到的机会均等,因此这些基本事件的出现是等可能的.
从五张卡片中任取两张,这两张卡片颜色不同且它们的标号之和小于4的结果为:(A,D),(A,E),(B,D),共3种.
所以这两张卡片颜色不同且它们的标号之和小于4的概率为.
(2)记F为标号为0的绿色卡片,从六张卡片中任取两张的所有可能的结果为:
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15种.
由于每一张卡片被取到的机会均等,因此这些基本事件的出现是等可能的.
从六张卡片中任取两张,这两张卡片颜色不同且它们的标号之和小于4的结果为:(A,D),(A,E),(B,D),(A,F),(B,F),(C,F),(D,F),(E,F),共8种.
所以这两张卡片颜色不同且它们的标号之和小于4的概率为.
21.解:(1)易知函数f(x)的定义域为(0,+∞).
当a=-2时,f(x)=x2-2lnx,f′(x)=2x-=.
当x变化时,f′(x)和f(x)的变化情况如下表:
x (0,1) 1 (1,+∞)
f′(x) - 0 +
f(x) 递减 极小值 递增
由上表可知,函数f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞),极小值是f(1)=1.
(2)由g(x)=x2+alnx+,得g′(x)=2x+-.
若函数g(x)为[1,+∞)上的单调增函数,则g′(x)≥0在[1,+∞)上恒成立,即不等式2x-+≥0在[1,+∞)上恒成立.也即a≥-2x2在[1,+∞)上恒成立.
令φ(x)=-2x2,则φ′(x)=--4x.
当x∈[1,+∞)时,φ′(x)=--4x<0,
∴φ(x)=-2x2在[1,+∞)上为减函数,
∴φ(x)max=φ(1)=0.
∴a≥0,即a的取值范围为[0,+∞).
22.解:(1)f′(x)=ex-a.令f′(x)=0得x=lna.
当x<lna时,f′(x)<0,f(x)单调递减;当x>lna时,f′(x)>0,f(x)单调递增.故当x=ln a时,f(x)取最小值f(lna)=a-alna.
于是对一切x∈R,f(x)≥1恒成立,当且仅当a-alna≥1. ①
令g(t)=t-tlnt,则g′(t)=-lnt.
当0<t<1时,g′(t)>0,g(t)单调递增;
当t>1时,g′(t)<0,g(t)单调递减.
故当t=1时,g(t)取最大值g(1)=1.因此,当且仅当a=1时,①式成立.
综上所述,a的取值集合为{1}.
(2)由题意知,k==-a.
令φ(x)=f′(x)-k=ex-,则
φ(x1)=- [-(x2-x1)-1],
φ(x2)= [-(x1-x2)-1].
令F(t)=et-t-1,则F′(t)=et-1.
当t<0时,F′(t)<0,F(t)单调递减;
当t>0时,F′(t)>0,F(t)单调递增.
故当t≠0时,F(t)>F(0)=0,即et-t-1>0.
从而-(x2-x1)-1>0,-(x1-x2)-1>0,又>0,>0,
所以φ(x1)<0,φ(x2)>0.
因为函数y=φ(x)在区间[x1,x2]上的图象是连续不断的一条曲线,所以存在x0∈(x1,x2),使φ(x0)=0,即f′(x0)=k成立.
同课章节目录
