鲁教版(五四制)数学七年级上册 4.1 .2无理数课件(共19张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 4.1 .2无理数课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 182.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 20:04:12 | ||
图片预览




文档简介
(共19张PPT)
无理数
第二课时
Contents
目录
01
02
03
04
旧知回顾
巩固练习
课堂小结
新知探究
例题讲解
05
06
拓展探究
1.有理数如何分类?
有理数
整数(如
分数(如
2.我们还学习过哪些不同的数? 如
圆周率 如a2=2,b2=5中
的a,b 不是整数,能不能化成分数呢?那么它们究竟是什么数呢?
,
… )
,
,
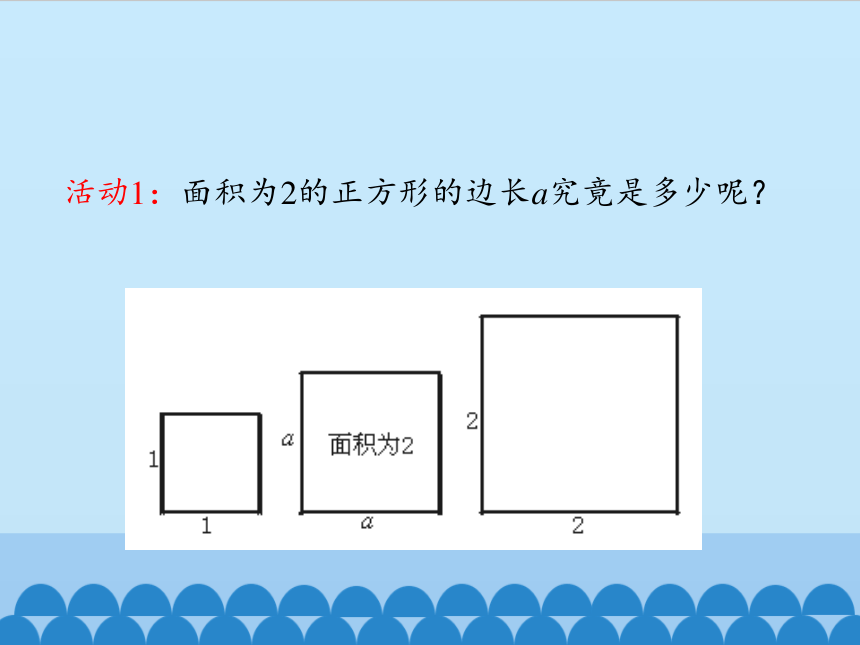
活动1:面积为2的正方形的边长a究竟是多少呢?
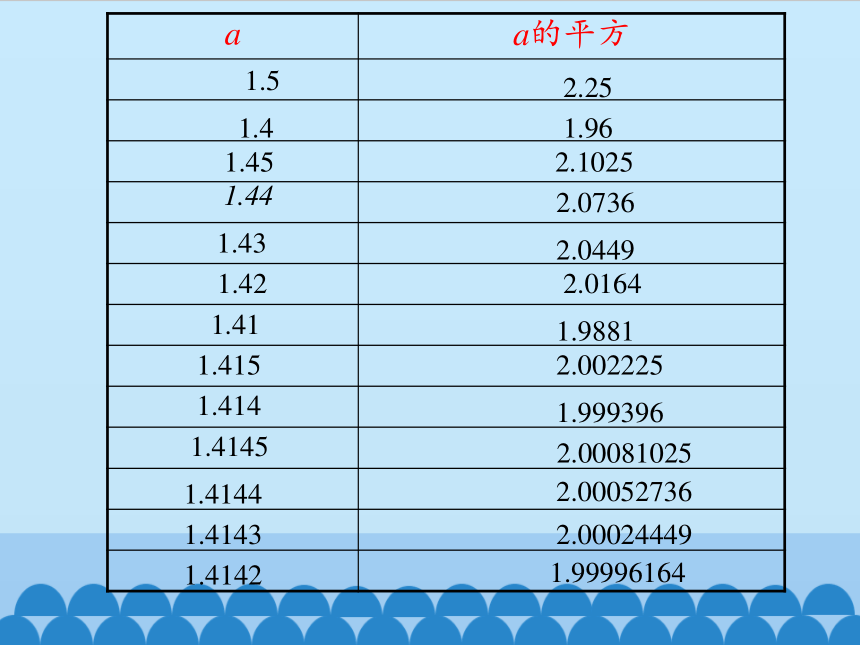
a a的平方
2.25
1.96
2.1025
2.0449
2.0736
2.0164
1.9881
2.002225
1.999396
2.00052736
2.00024449
1.99996164
2.00081025
1.4
1.5
1.45
1.44
1.43
1.42
1.41
1.415
1.414
1.4145
1.4144
1.4143
1.4142
(1)3个正方形的边长之间有怎样的大小关系?说说你的理由。
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索。
(3)小明根据他的探索过程整理出如下的表格,你的结果呢?
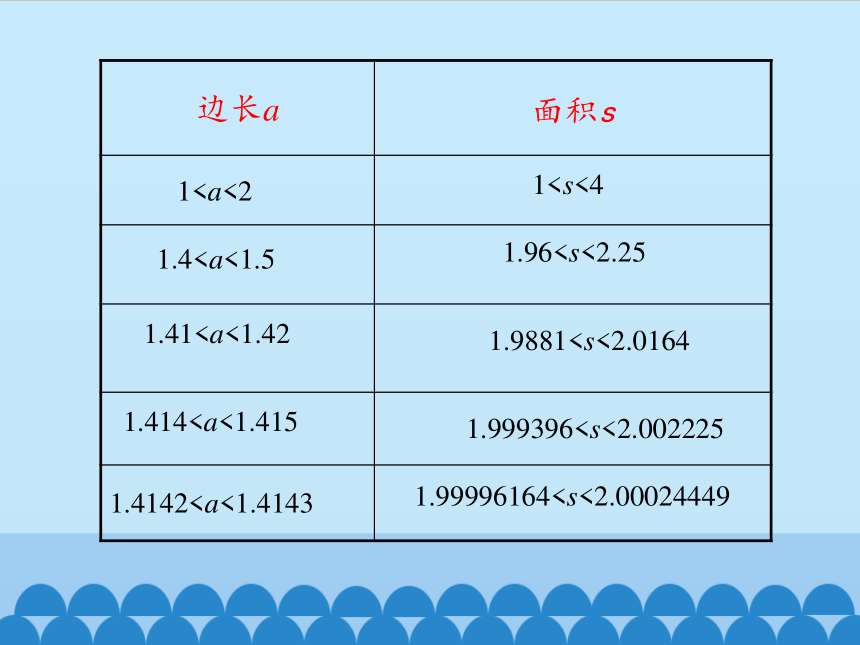
边长a 面积s
111.41.961.411.98811.4141.9993961.41421.99996164还可以继续算下去吗? a可能是有限小数吗?
事实上,a =1.41421356……它是一个无限不循环小数。
请大家用上面的方法:
(1)估计面积为5的正方形的边长b的值(精确到十分位),并用计算器验证你的估计。
(2)如果结果精确到百分位呢?
做一做
b=2.23606797……它是一个无限不循环小数.同样,对于体积为2的正方体,借助计算器,可以得到它的棱长c=1.25992105……,它也是一个无限不循环小数。
事实上,
活动2:
分数化成小数,最终此小数的形式有几种情况?
把下列各数表示成小数,你发现了什么?
结论:事实上,有理数总可以用有限小数或无限循环小数表示。反过来,任何有限小数或无限循环小数也都是有理数。
即任何有限小数或无限循环小数都是有理数.所以a、b不是有理数。
除了像上面的数a,b,c是无理数外,我们十分熟悉的圆周率π=3.14159265……也是一个无限不循环小数,因此它也是一个无理数。再如0.585885888588885……
(相邻两个5之间8的个数逐次加1),也是无理数。
无限不循环小数叫无理数。
分一分
到目前为止所学过的数可以分为几类?
按小数的形式来分
有理数:有限小数或无限循环小数
无理数:无限不循环小数
数
整数
分数
例1 下列各数中,哪些是有理数?哪些是无理数?
(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数。 ( )
判断题
╳
√
√
╳
1.无理数是无限不循环小数,有理数是有限小数或无限循环小数。
2.任何一个有理数都可以化成分数 形式(
q ≠0, p,q 为整数且互质),而无理数则不能。
强调
1.课本随堂练习。
2.已知:下列各数
(1)写出所有有理数;
(2)写出所有无理数;
(3)把这些数按由小到大的顺序排列起来,
并用符号“<”连接。
本节课你有什么收获?
1.无理数的定义。
2.你是怎样判断一个数是无理数,还是有理数的?
3.请把已学过的数怎样分类?
谢 谢
无理数
第二课时
Contents
目录
01
02
03
04
旧知回顾
巩固练习
课堂小结
新知探究
例题讲解
05
06
拓展探究
1.有理数如何分类?
有理数
整数(如
分数(如
2.我们还学习过哪些不同的数? 如
圆周率 如a2=2,b2=5中
的a,b 不是整数,能不能化成分数呢?那么它们究竟是什么数呢?
,
… )
,
,
活动1:面积为2的正方形的边长a究竟是多少呢?
a a的平方
2.25
1.96
2.1025
2.0449
2.0736
2.0164
1.9881
2.002225
1.999396
2.00052736
2.00024449
1.99996164
2.00081025
1.4
1.5
1.45
1.44
1.43
1.42
1.41
1.415
1.414
1.4145
1.4144
1.4143
1.4142
(1)3个正方形的边长之间有怎样的大小关系?说说你的理由。
(2)边长a的整数部分是几?十分位是几?百分位呢?千分位呢?……借助计算器进行探索。
(3)小明根据他的探索过程整理出如下的表格,你的结果呢?
边长a 面积s
1
事实上,a =1.41421356……它是一个无限不循环小数。
请大家用上面的方法:
(1)估计面积为5的正方形的边长b的值(精确到十分位),并用计算器验证你的估计。
(2)如果结果精确到百分位呢?
做一做
b=2.23606797……它是一个无限不循环小数.同样,对于体积为2的正方体,借助计算器,可以得到它的棱长c=1.25992105……,它也是一个无限不循环小数。
事实上,
活动2:
分数化成小数,最终此小数的形式有几种情况?
把下列各数表示成小数,你发现了什么?
结论:事实上,有理数总可以用有限小数或无限循环小数表示。反过来,任何有限小数或无限循环小数也都是有理数。
即任何有限小数或无限循环小数都是有理数.所以a、b不是有理数。
除了像上面的数a,b,c是无理数外,我们十分熟悉的圆周率π=3.14159265……也是一个无限不循环小数,因此它也是一个无理数。再如0.585885888588885……
(相邻两个5之间8的个数逐次加1),也是无理数。
无限不循环小数叫无理数。
分一分
到目前为止所学过的数可以分为几类?
按小数的形式来分
有理数:有限小数或无限循环小数
无理数:无限不循环小数
数
整数
分数
例1 下列各数中,哪些是有理数?哪些是无理数?
(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数。 ( )
判断题
╳
√
√
╳
1.无理数是无限不循环小数,有理数是有限小数或无限循环小数。
2.任何一个有理数都可以化成分数 形式(
q ≠0, p,q 为整数且互质),而无理数则不能。
强调
1.课本随堂练习。
2.已知:下列各数
(1)写出所有有理数;
(2)写出所有无理数;
(3)把这些数按由小到大的顺序排列起来,
并用符号“<”连接。
本节课你有什么收获?
1.无理数的定义。
2.你是怎样判断一个数是无理数,还是有理数的?
3.请把已学过的数怎样分类?
谢 谢
