2021-2022学年高一上学期数学北师大版必修1 第一章 集合 3.1 交集与并集 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版必修1 第一章 集合 3.1 交集与并集 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 678.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 14:29:34 | ||
图片预览




文档简介
(共20张PPT)
3.1交集与并集
教学分析
本节从实例出发,引出交集与并集的定义,并同时给出借助Venn图、数轴等工具求两个集合的交集、并集,通过求集合的交集、并集,培养学生运用集合解决实际问题的能力。
三维目标
理解并掌握两个集合交集、并集的定义,会求两个简单集合的交集并集,掌握求简单的两个集合交集并集的方法。熟练运用Venn图,数轴等数学工具求两个集合的交集并集。
运用求集合的交集,并集的数学方法,去解决实际问题,提高学生分析问题和解决问题的能力,培养学生应用数学的能力。
教学重点:两个集合交集并集的定义,
掌握助Venn图,数轴等数学工具求
两个集合的交集并集。
教学难点:集合的综合运算。
教学过程
一、导入新课
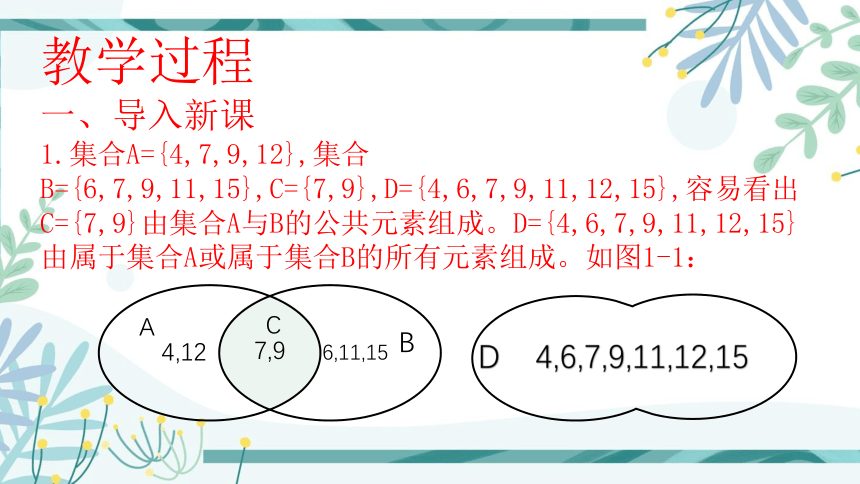
1.集合A={4,7,9,12},集合 B={6,7,9,11,15},C={7,9},D={4,6,7,9,11,12,15},容易看出C={7,9}由集合A与B的公共元素组成。D={4,6,7,9,11,12,15}由属于集合A或属于集合B的所有元素组成。如图1-1:
7,9
4,12
6,11,15
A
B
C
D 4,6,7,9,11,12,15
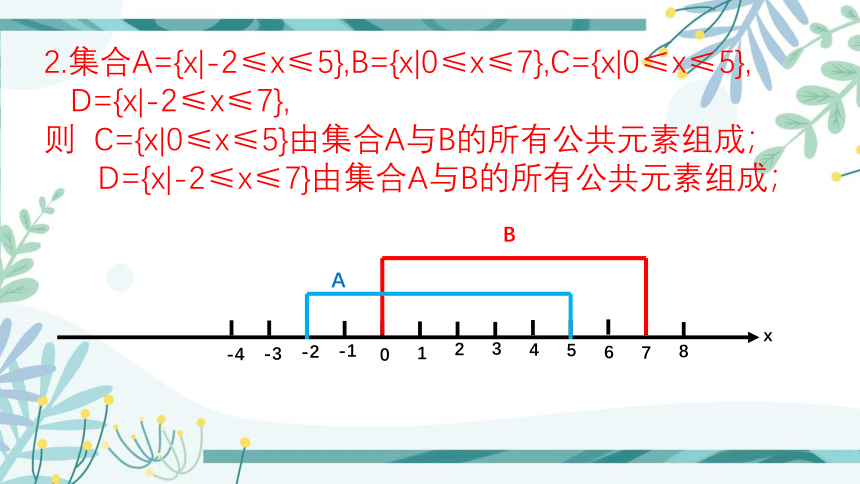
2.集合A={x|-2≤x≤5},B={x|0≤x≤7},C={x|0≤x≤5},
D={x|-2≤x≤7},
则 C={x|0≤x≤5}由集合A与B的所有公共元素组成;
D={x|-2≤x≤7}由集合A与B的所有公共元素组成;
1
-1
-2
-3
-4
0
2
3
4
5
6
7
8
x
A
B
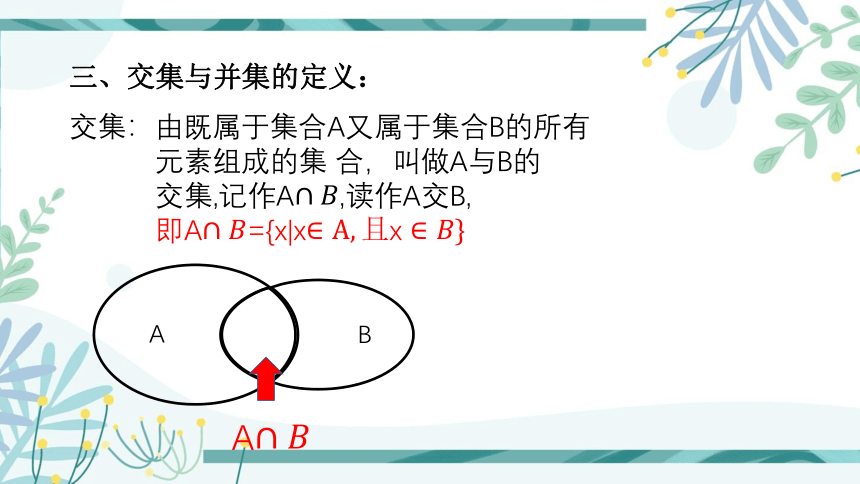
三、交集与并集的定义:
交集:由既属于集合A又属于集合B的所有
元素组成的集 合,叫做A与B的
交集,记作A,读作A交B,
即A={x|xx
A
A
B
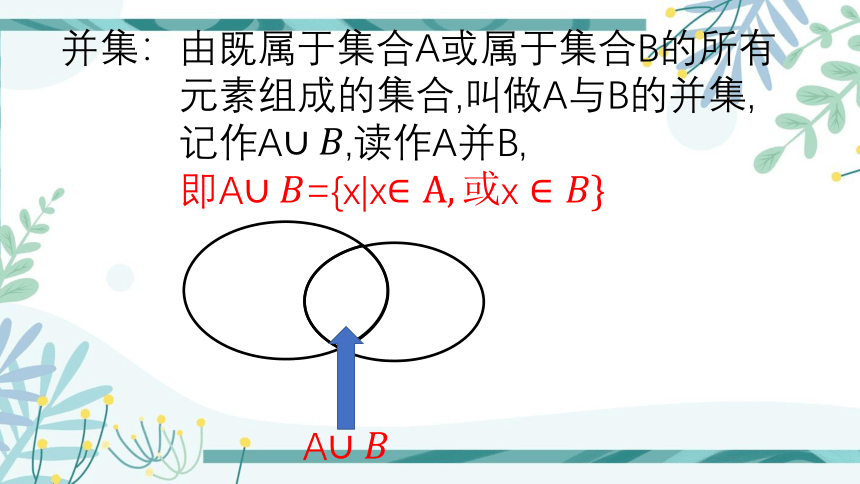
并集:由既属于集合A或属于集合B的所有
元素组成的集合,叫做A与B的并集,
记作A,读作A并B,
即A={x|xx
A
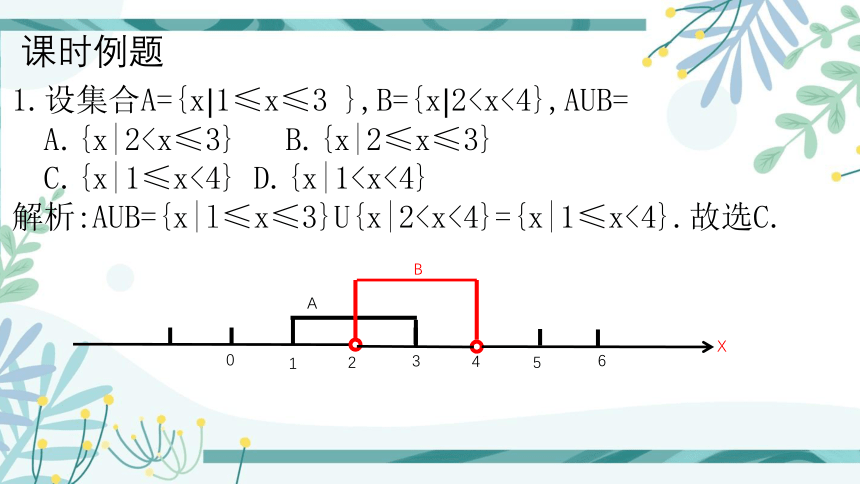
1.设集合A={x1≤x≤3 },B={x2A.{x|2C.{x|1≤x<4} D.{x|1解析:AUB={x|l≤x≤3}U{x|2课时例题
1
0
3
6
2
4
5
B
A
X
2.已知集合A={1,2,3,5,7,11},B={x|3A.2 B.3 C.4 D.4
解析:因为A∩B={5,7,11},所以A∩B中元素的个数为3.
故选B.
3.已知函数y=x,x[a.b],那么集合{(x,y)ly=x,x∈[a ,b]
|x=2}中元素的个数为( ).
A.1 B.0 C.0或1 D.1或2
解析:由函数定义知,当x=2∈[a .b]时,函数y=x的图象与直线x=2有一个交点,当x=2[a.b]时,函数y=x的图象与直线x=2没有交点.
答案 C
设A={x-4x+3≤0},
B=(x|0<3—2x<1},则图中阴影部分表示的集合为……( )
A.{x|x< B.{x|1C.{x|1≤x } D.{x|≤x }
4.
解析 A=
{x|x2-4x+3≤0}={x|1≤x≤3}
B={x|0<3-2x<1}={x|1U
U
B
A
5.已知集合M={x|+=1},N={y|+=1},则
M
A. B.{(4,0),(3,0)
C.[-3,3] D.[-4,4]
解析 由曲线方程,知M={x|≤1} =[-4,4]
又N={y|+=1}=R,∴M=[-4,4].
6.设集合A={x|-1≤x<2},B={x|xa的取值范围是……( ).
A.(-1,2] B.(2,+)
C.[-1,+) D.(-1,+)
解析 因为AB,所以集合A,B有公共元素,
利用数轴可知a>-1.
A
B
X
-2
-1
2
a
7.设集合A={x|x>-1},B={x|-2A.{x|x>-2} B.{x|x>-1}
C.{x|-2-1
-2
2
利用数轴可得AB={x|x>-2}
8.设S={x|2x+1>0},T={x|3x-5<0},则ST=……( )
解析 S={x|x>-},T={x|x<}
-
答案:{x|-9.定义集合A与B的运算A*B={xlx∈A或x∈B,且xA∩B},则(A * B)*A等于………( ).
A.A∩B B.AUB
C.A D.B
解析:设A={1,2,3,4},B={1,2,5,6,7},则A*B={3,4,5,6,7},于是(A* B)*A={1,2,5,6,7}=B.
答案:D
点评:解决新定义集合运算问题的关键是抓住新运算定义的本质,本题A*B的本质就是集合A与B的并集中除去它们公共元素组成的集合.
10.已知集合集合P={x|1≤xQ={x|x2+x-6=0},
则PQ等于……( )
A.{1,2,3} B.{2,3}
B.{1,2} D.{2}
解析:明确集合P,Q的运算,依据交集的定义的
P={1,2,3,4,5,6,7,8,9,10},Q={-3,2},
则PQ={2}
课时小结
理解并掌握集合的交集并集的概念。
借助Venn图,数轴等数学工具求简单集合的交集并集。
3.1交集与并集
教学分析
本节从实例出发,引出交集与并集的定义,并同时给出借助Venn图、数轴等工具求两个集合的交集、并集,通过求集合的交集、并集,培养学生运用集合解决实际问题的能力。
三维目标
理解并掌握两个集合交集、并集的定义,会求两个简单集合的交集并集,掌握求简单的两个集合交集并集的方法。熟练运用Venn图,数轴等数学工具求两个集合的交集并集。
运用求集合的交集,并集的数学方法,去解决实际问题,提高学生分析问题和解决问题的能力,培养学生应用数学的能力。
教学重点:两个集合交集并集的定义,
掌握助Venn图,数轴等数学工具求
两个集合的交集并集。
教学难点:集合的综合运算。
教学过程
一、导入新课
1.集合A={4,7,9,12},集合 B={6,7,9,11,15},C={7,9},D={4,6,7,9,11,12,15},容易看出C={7,9}由集合A与B的公共元素组成。D={4,6,7,9,11,12,15}由属于集合A或属于集合B的所有元素组成。如图1-1:
7,9
4,12
6,11,15
A
B
C
D 4,6,7,9,11,12,15
2.集合A={x|-2≤x≤5},B={x|0≤x≤7},C={x|0≤x≤5},
D={x|-2≤x≤7},
则 C={x|0≤x≤5}由集合A与B的所有公共元素组成;
D={x|-2≤x≤7}由集合A与B的所有公共元素组成;
1
-1
-2
-3
-4
0
2
3
4
5
6
7
8
x
A
B
三、交集与并集的定义:
交集:由既属于集合A又属于集合B的所有
元素组成的集 合,叫做A与B的
交集,记作A,读作A交B,
即A={x|xx
A
A
B
并集:由既属于集合A或属于集合B的所有
元素组成的集合,叫做A与B的并集,
记作A,读作A并B,
即A={x|xx
A
1.设集合A={x1≤x≤3 },B={x2
1
0
3
6
2
4
5
B
A
X
2.已知集合A={1,2,3,5,7,11},B={x|3
解析:因为A∩B={5,7,11},所以A∩B中元素的个数为3.
故选B.
3.已知函数y=x,x[a.b],那么集合{(x,y)ly=x,x∈[a ,b]
|x=2}中元素的个数为( ).
A.1 B.0 C.0或1 D.1或2
解析:由函数定义知,当x=2∈[a .b]时,函数y=x的图象与直线x=2有一个交点,当x=2[a.b]时,函数y=x的图象与直线x=2没有交点.
答案 C
设A={x-4x+3≤0},
B=(x|0<3—2x<1},则图中阴影部分表示的集合为……( )
A.{x|x< B.{x|1
4.
解析 A=
{x|x2-4x+3≤0}={x|1≤x≤3}
B={x|0<3-2x<1}={x|1
U
B
A
5.已知集合M={x|+=1},N={y|+=1},则
M
A. B.{(4,0),(3,0)
C.[-3,3] D.[-4,4]
解析 由曲线方程,知M={x|≤1} =[-4,4]
又N={y|+=1}=R,∴M=[-4,4].
6.设集合A={x|-1≤x<2},B={x|x
A.(-1,2] B.(2,+)
C.[-1,+) D.(-1,+)
解析 因为AB,所以集合A,B有公共元素,
利用数轴可知a>-1.
A
B
X
-2
-1
2
a
7.设集合A={x|x>-1},B={x|-2
C.{x|-2
-2
2
利用数轴可得AB={x|x>-2}
8.设S={x|2x+1>0},T={x|3x-5<0},则ST=……( )
解析 S={x|x>-},T={x|x<}
-
答案:{x|-
A.A∩B B.AUB
C.A D.B
解析:设A={1,2,3,4},B={1,2,5,6,7},则A*B={3,4,5,6,7},于是(A* B)*A={1,2,5,6,7}=B.
答案:D
点评:解决新定义集合运算问题的关键是抓住新运算定义的本质,本题A*B的本质就是集合A与B的并集中除去它们公共元素组成的集合.
10.已知集合集合P={x|1≤xQ={x|x2+x-6=0},
则PQ等于……( )
A.{1,2,3} B.{2,3}
B.{1,2} D.{2}
解析:明确集合P,Q的运算,依据交集的定义的
P={1,2,3,4,5,6,7,8,9,10},Q={-3,2},
则PQ={2}
课时小结
理解并掌握集合的交集并集的概念。
借助Venn图,数轴等数学工具求简单集合的交集并集。
