人教A版 选择性必修第二册 5.3 5.3.1 函数的单调性 课件(共50张PPT)
文档属性
| 名称 | 人教A版 选择性必修第二册 5.3 5.3.1 函数的单调性 课件(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 07:21:46 | ||
图片预览











文档简介
(共50张PPT)
第五章 一元函数的导数及其应用
5.3 导数在研究函数中的应用
5.3.1 函数的单调性
学习指导 核心素养
1.通过数形结合感受导数与函数单调性的关系. 2.掌握利用导数判断函数单调性的方法. 3.能利用导数求不超过三次的多项式函数的单调区间. 1.直观想象:导数符号和函数单调性的关系.
2.数学运算、逻辑推理:研究函数的单调性.
1.函数的单调性与其导数的正负之间的关系
定义在区间(a,b)上的函数y=f(x):
增
减
2.利用导数判断函数的单调性
一般情况下,我们可以通过如下步骤判断函数y=f(x)的单调性:
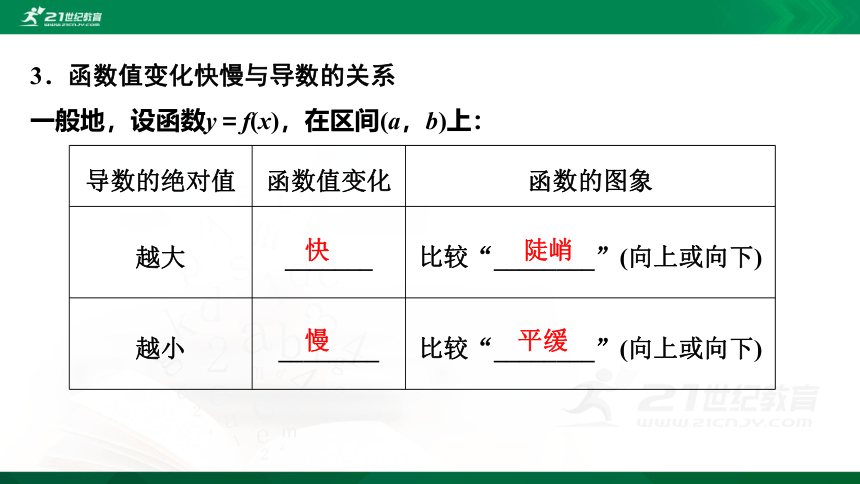
导数的绝对值 函数值变化 函数的图象
越大 _______ 比较“________”(向上或向下)
越小 ________ 比较“________”(向上或向下)
3.函数值变化快慢与导数的关系
一般地,设函数y=f(x),在区间(a,b)上:
快
陡峭
慢
平缓
1.如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?
提示:f(x)是常数函数.
2.在某个区间内f′(x)>0是函数f(x)在此区间内单调递增的什么条件?
提示:充分不必要条件,如函数f(x)=x3在(-∞,+∞)上单调递增,而f′(x)=3x2≥0.
1.判断正误(正确的打“√”,错误的打“×”)
(1)函数f(x)在定义域上都有f′(x)<0,则函数f(x)在定义域上单调递减.
( )
(2)函数f(x)在某区间上单调递增,则一定有f′(x)>0.( )
(3)函数在某个区间上变化越快,函数在这个区间上的导数的绝对值越
大.( )
(4)函数y=x3+x的单调递增区间为(-∞,+∞).( )
×
√
×
√
√
2.下列函数中,在(0,+∞)上单调递增的是( )
A.y=sin x B.y=xex
C.y=x3-x D.y=ln x-x
√
探究点1 导数与函数图象的关系
[问题探究]
如何从导数的几何意义理解函数的单调性与导数正负的关系?
探究感悟:如果f′(x)>0,即切线的斜率为正,则切线的倾斜角为锐角,曲线呈上升趋势,即函数单调递增.
如果f′(x)<0,即切线的斜率为负,则切线的倾斜角为钝角,曲线呈下降趋势,即函数单调递减.
已知f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )
√
(1)函数的单调性与其导函数的正负之间的关系:在某个区间(a,b)内,若f′(x)>0,则y=f(x)在区间(a,b)上单调递增;如果f′(x)<0,则y=f(x)在区间(a,b)上单调递减;若恒有f′(x)=0,则y=f(x)是常数函数,不具有单调性.
(2)函数图象变化得越快,f′(x)的绝对值越大,不是f′(x) 的值越大.
√
解析:由函数的图象可知:当x<0时,函数单调递增,导数始终为正;当x>0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.
√
√
(1)如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字隔开.
(2)讨论含有参数的函数的单调性,通常归结为求含参数不等式的解集问题,而对含有参数的不等式要针对具体情况进行讨论,但要始终注意定义域对函数单调性的影响以及分类讨论的标准.
2.设函数f(x)=ex-ax-2,求f(x)的单调区间.
解:f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,
所以f(x)在(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
所以f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
综上所述,当a≤0时,函数f(x)的单调递增区间为(-∞,+∞),无单调递减区间;
当a>0时,f(x)的单调递减区间为(-∞,ln a),
单调递增区间为(ln a,+∞).
探究点3 已知函数的单调性求参数
[问题探究]
“函数y=f(x)的单调递减区间为(a,b)”与“函数y=f(x) 在(a,b)上单调递减”是否相同?
探究感悟:不相同.前者(a,b)为不等式f′(x)≤0的解集;后者(a,b)为不等式f′(x)≤0的解集的子集.
√
已知函数单调性求参数的两种方法
(1)分离参数法
f(x)在(a,b)上单调递增(减)等价于f′(x)≥0(f′(x)≤0)在(a,b)上恒成立,将参数分离后可转化为求其函数的值域问题,注意验证等号是否成立.
(2)子集法
若能较容易地求出函数的单调区间,则可利用子区间来解决.若f(x)在
(a,b)上单调递增(减),则区间(a,b)是相应单调区间的子集.
√
√
1.(多选)函数f(x)=(x-3)ex在下列区间上单调递增的是( )
A.(-∞,2) B.(0,3)
C.(3,4) D.(2,+∞)
√
解析:因为f′(x)=ex+(x-3)ex=(x-2)ex,
由f′(x)>0得(x-2)ex>0,
所以x>2.
所以f(x)的单调递增区间为(2,+∞),CD符合.
√
√
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第五章 一元函数的导数及其应用
5.3 导数在研究函数中的应用
5.3.1 函数的单调性
学习指导 核心素养
1.通过数形结合感受导数与函数单调性的关系. 2.掌握利用导数判断函数单调性的方法. 3.能利用导数求不超过三次的多项式函数的单调区间. 1.直观想象:导数符号和函数单调性的关系.
2.数学运算、逻辑推理:研究函数的单调性.
1.函数的单调性与其导数的正负之间的关系
定义在区间(a,b)上的函数y=f(x):
增
减
2.利用导数判断函数的单调性
一般情况下,我们可以通过如下步骤判断函数y=f(x)的单调性:
导数的绝对值 函数值变化 函数的图象
越大 _______ 比较“________”(向上或向下)
越小 ________ 比较“________”(向上或向下)
3.函数值变化快慢与导数的关系
一般地,设函数y=f(x),在区间(a,b)上:
快
陡峭
慢
平缓
1.如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?
提示:f(x)是常数函数.
2.在某个区间内f′(x)>0是函数f(x)在此区间内单调递增的什么条件?
提示:充分不必要条件,如函数f(x)=x3在(-∞,+∞)上单调递增,而f′(x)=3x2≥0.
1.判断正误(正确的打“√”,错误的打“×”)
(1)函数f(x)在定义域上都有f′(x)<0,则函数f(x)在定义域上单调递减.
( )
(2)函数f(x)在某区间上单调递增,则一定有f′(x)>0.( )
(3)函数在某个区间上变化越快,函数在这个区间上的导数的绝对值越
大.( )
(4)函数y=x3+x的单调递增区间为(-∞,+∞).( )
×
√
×
√
√
2.下列函数中,在(0,+∞)上单调递增的是( )
A.y=sin x B.y=xex
C.y=x3-x D.y=ln x-x
√
探究点1 导数与函数图象的关系
[问题探究]
如何从导数的几何意义理解函数的单调性与导数正负的关系?
探究感悟:如果f′(x)>0,即切线的斜率为正,则切线的倾斜角为锐角,曲线呈上升趋势,即函数单调递增.
如果f′(x)<0,即切线的斜率为负,则切线的倾斜角为钝角,曲线呈下降趋势,即函数单调递减.
已知f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )
√
(1)函数的单调性与其导函数的正负之间的关系:在某个区间(a,b)内,若f′(x)>0,则y=f(x)在区间(a,b)上单调递增;如果f′(x)<0,则y=f(x)在区间(a,b)上单调递减;若恒有f′(x)=0,则y=f(x)是常数函数,不具有单调性.
(2)函数图象变化得越快,f′(x)的绝对值越大,不是f′(x) 的值越大.
√
解析:由函数的图象可知:当x<0时,函数单调递增,导数始终为正;当x>0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.
√
√
(1)如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字隔开.
(2)讨论含有参数的函数的单调性,通常归结为求含参数不等式的解集问题,而对含有参数的不等式要针对具体情况进行讨论,但要始终注意定义域对函数单调性的影响以及分类讨论的标准.
2.设函数f(x)=ex-ax-2,求f(x)的单调区间.
解:f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,
所以f(x)在(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
所以f(x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.
综上所述,当a≤0时,函数f(x)的单调递增区间为(-∞,+∞),无单调递减区间;
当a>0时,f(x)的单调递减区间为(-∞,ln a),
单调递增区间为(ln a,+∞).
探究点3 已知函数的单调性求参数
[问题探究]
“函数y=f(x)的单调递减区间为(a,b)”与“函数y=f(x) 在(a,b)上单调递减”是否相同?
探究感悟:不相同.前者(a,b)为不等式f′(x)≤0的解集;后者(a,b)为不等式f′(x)≤0的解集的子集.
√
已知函数单调性求参数的两种方法
(1)分离参数法
f(x)在(a,b)上单调递增(减)等价于f′(x)≥0(f′(x)≤0)在(a,b)上恒成立,将参数分离后可转化为求其函数的值域问题,注意验证等号是否成立.
(2)子集法
若能较容易地求出函数的单调区间,则可利用子区间来解决.若f(x)在
(a,b)上单调递增(减),则区间(a,b)是相应单调区间的子集.
√
√
1.(多选)函数f(x)=(x-3)ex在下列区间上单调递增的是( )
A.(-∞,2) B.(0,3)
C.(3,4) D.(2,+∞)
√
解析:因为f′(x)=ex+(x-3)ex=(x-2)ex,
由f′(x)>0得(x-2)ex>0,
所以x>2.
所以f(x)的单调递增区间为(2,+∞),CD符合.
√
√
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
