2021-2022学年人教版数学八年级下册20.1.1加权平均数课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册20.1.1加权平均数课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-12 20:10:27 | ||
图片预览







文档简介
(共25张PPT)
八年级数学
——平均数
2019年12月以来,新型冠状病毒的出现,导致大面积的人群感染不明原因肺炎,为此,国家在党中央的集中统一领导下采取了各项预防和治疗措施积极应对,对医院、商场等公共场所要求进行全面消毒,以保证公民的人生建康。某医院积极响应,准备采购一批消毒液对医院各个区域进行全面消毒,而如何从品类众多的消毒液商品中进行合理选择采购呢?
20.1.1平均数
第二十章 数据的分析
第1课时 平均数和加权平均数
学习目标
1.理解数据的权和加权平均数的概念,体会权的作用
2.明确加权平均数与算数平均数的关系,掌握加权平
均数的计算方法.(重点、难点)
3.进一步认识数据的作用,体会统计思想
新课引入
1.数据2、3、4、1、2的平均数是____,
这个平均数叫做 平均数.
2.4
算术
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数.记为:
即
新课讲解
1.平均数与加权平均数
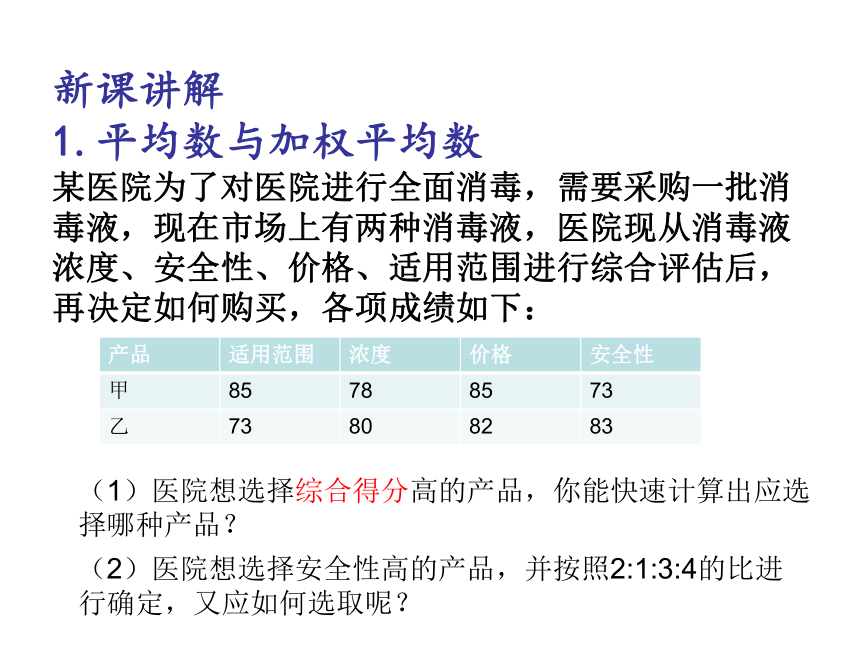
某医院为了对医院进行全面消毒,需要采购一批消
毒液,现在市场上有两种消毒液,医院现从消毒液
浓度、安全性、价格、适用范围进行综合评估后,
再决定如何购买,各项成绩如下:
产品 适用范围 浓度 价格 安全性
甲 85 78 85 73
乙 73 80 82 83
(1)医院想选择综合得分高的产品,你能快速计算出应选
择哪种产品?
(2)医院想选择安全性高的产品,并按照2:1:3:4的比进 行确定,又应如何选取呢?
通过计算发现甲的平均成绩高,所以选择甲种消毒液。
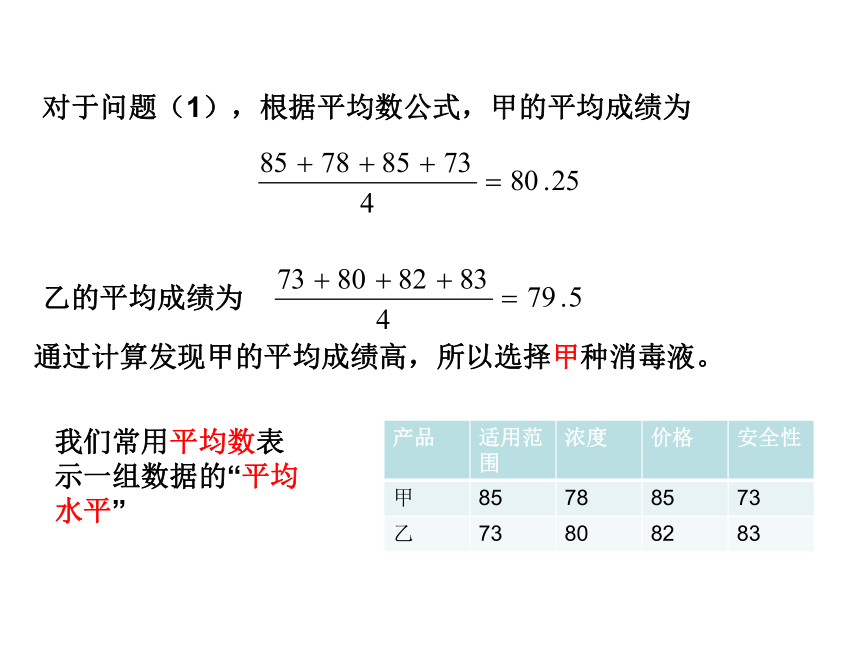
对于问题(1),根据平均数公式,甲的平均成绩为
乙的平均成绩为
产品 适用范围 浓度 价格 安全性
甲 85 78 85 73
乙 73 80 82 83
我们常用平均数表示一组数据的“平均水平”
对于问题(2),因为按照2:1:3:4的比确定,此时用
算数平均数来衡量他们的成绩合理吗?
乙的平均成绩为
因为乙的平均得分比甲高,所以应选择乙消毒液
产品 适用范围 浓度 价格 安全性
甲 85 78 85 73
乙 73 80 82 83
适用范围、浓度、价格、安全性按照2:1:3:4的比来确定
甲的平均成绩为
上述问题(1)是利用平均数的公式计算平均成绩,其中的每个数据被认为同等重要,而问题(2)是根据实际需要对不同类型的数据赋予与其重要程度相应的比重,其中的2,1,3,4,分别称为四项成绩的权,相应的平均数79.5, 80.4分别称为甲和乙的四项成绩的加权平均数。
归纳: 一般的,若n个数x1,x2,……xn的权分别是w1,w2,……wn,则
叫做这n个数的加权平均数
思考 能把这种加权平均数的计算方法推广到一般吗?
思考
如果这家医院对无人区域消毒时,主要考虑价格时,按照2:2:3:3的比例确定,那么医院又会选择哪种产品呢?与上述问题中的(1)(2)相比较,你体会到权的作用了吗?
同样一张测试成绩单,由于各个数据所赋予
的权数不同,造成的录取结果截然不同
数据的权能够反映数据的相对重要程度
练习1、晨光中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末成绩占50%。小桐的三项成绩(百分制)依次是95分、90分、85分,小桐这学期的体育成绩是多少?
解:
提问:你能说说算数平均数与加权平均数的区别和
联系吗?
1.算数平均数是加权平均数的一种特殊情况(它特殊在各项的
权相等
2.在实际问题中,各项权不相等时,计算平均数时就要采用加权
平均数,当各项权相等时,计算平均数就要采用算数平均数。
练习2、疫情期间,某医院欲招聘医生,对甲、乙候选人进行了面视和笔试,他们的成绩如下表所示
(1)如果医院认为面试和笔试同等重要,从他们的成绩看,谁将被录取
候选人 测试成绩(百分制)
操作 笔试
甲 86 90
乙 92 83
(2)如果医院认为,作为医生操作的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取。
(2)如果医院认为,作为医生操作的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取。
(1)如果医院认为操作和笔试同等重要,从他们的成绩看,谁将被录取
在求n个数的平均数时,如果x1出现f1次,x2出现f2次,……xk出现fk次(这个f1+f2+……fk=n),那么这n个数的平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…fk分别叫做x1,x2,…,xk的权
2.加权平均数的其他形式
例2.新型冠状病毒肺炎发生以后,武汉成为疫情重灾区,医护人员数量告急,在党中央的统一领导下,全国上下积极支援,为了了解支援医护人员年龄情况,做了一次年龄调查,结果如下:33岁8人,34岁16人,35岁24人,36岁2人,求该支援医疗队的平均年龄(结果取整数)
解:这支支援医疗队的平均年龄为
(岁)
练习3.下表是校女子排球队员的年龄分布,求校女子排球队员的平均年龄。(结果取整数)
年龄/岁 13 14 15 16
频数 1 4 5 2
(岁)
解:
随堂练习
1.一组数据为10, 8, 9, 12, 13, 10, 8,则这组数据的
平均数是 .
2.已知一组数据4, 13, 24的权数分别是
则这组数据的加权平均数是 .
10
17
3.某公司有15名员工,他们所在的部门及相应每人所创造的年利润(万元)如下表:
部门 A B C D E F G
人数 1 1 2 2 2 2 5
利润 200 40 25 20 15 15 12
该公司每人所创造的年利润的平均数是 万元。
30
4.某次医术技能大赛,两名选手的成绩如下:
选手 测试成绩
创新 基本功 综合知识
A 72 85 67
B 85 74 70
(1)若按三项平均值取第一名,则 是第一名
B
(2)若三项测试得分按3:6:1的比例确定个人的测试成绩,此时第一名是谁呢?
解:
所以,此时第一名是A
权的常见形式有哪些?
1.比例(如2:1:3:4)
2.百分数(如50%、40% 、10%.)
3.频数(如8、16、24、2.)
课堂小结
一、两种平均数的求法:
算术平均数
加权平均数
加权平均数中的“权”的三种表现形式:
(1)频数 (2)百分比 (3)比例
二、“权”的意义:
表示数据的“重要程度”.
作业:
P113-练习1
P121-第1、4、5题
本节课结束
同学们,再见!
八年级数学
——平均数
2019年12月以来,新型冠状病毒的出现,导致大面积的人群感染不明原因肺炎,为此,国家在党中央的集中统一领导下采取了各项预防和治疗措施积极应对,对医院、商场等公共场所要求进行全面消毒,以保证公民的人生建康。某医院积极响应,准备采购一批消毒液对医院各个区域进行全面消毒,而如何从品类众多的消毒液商品中进行合理选择采购呢?
20.1.1平均数
第二十章 数据的分析
第1课时 平均数和加权平均数
学习目标
1.理解数据的权和加权平均数的概念,体会权的作用
2.明确加权平均数与算数平均数的关系,掌握加权平
均数的计算方法.(重点、难点)
3.进一步认识数据的作用,体会统计思想
新课引入
1.数据2、3、4、1、2的平均数是____,
这个平均数叫做 平均数.
2.4
算术
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数.记为:
即
新课讲解
1.平均数与加权平均数
某医院为了对医院进行全面消毒,需要采购一批消
毒液,现在市场上有两种消毒液,医院现从消毒液
浓度、安全性、价格、适用范围进行综合评估后,
再决定如何购买,各项成绩如下:
产品 适用范围 浓度 价格 安全性
甲 85 78 85 73
乙 73 80 82 83
(1)医院想选择综合得分高的产品,你能快速计算出应选
择哪种产品?
(2)医院想选择安全性高的产品,并按照2:1:3:4的比进 行确定,又应如何选取呢?
通过计算发现甲的平均成绩高,所以选择甲种消毒液。
对于问题(1),根据平均数公式,甲的平均成绩为
乙的平均成绩为
产品 适用范围 浓度 价格 安全性
甲 85 78 85 73
乙 73 80 82 83
我们常用平均数表示一组数据的“平均水平”
对于问题(2),因为按照2:1:3:4的比确定,此时用
算数平均数来衡量他们的成绩合理吗?
乙的平均成绩为
因为乙的平均得分比甲高,所以应选择乙消毒液
产品 适用范围 浓度 价格 安全性
甲 85 78 85 73
乙 73 80 82 83
适用范围、浓度、价格、安全性按照2:1:3:4的比来确定
甲的平均成绩为
上述问题(1)是利用平均数的公式计算平均成绩,其中的每个数据被认为同等重要,而问题(2)是根据实际需要对不同类型的数据赋予与其重要程度相应的比重,其中的2,1,3,4,分别称为四项成绩的权,相应的平均数79.5, 80.4分别称为甲和乙的四项成绩的加权平均数。
归纳: 一般的,若n个数x1,x2,……xn的权分别是w1,w2,……wn,则
叫做这n个数的加权平均数
思考 能把这种加权平均数的计算方法推广到一般吗?
思考
如果这家医院对无人区域消毒时,主要考虑价格时,按照2:2:3:3的比例确定,那么医院又会选择哪种产品呢?与上述问题中的(1)(2)相比较,你体会到权的作用了吗?
同样一张测试成绩单,由于各个数据所赋予
的权数不同,造成的录取结果截然不同
数据的权能够反映数据的相对重要程度
练习1、晨光中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末成绩占50%。小桐的三项成绩(百分制)依次是95分、90分、85分,小桐这学期的体育成绩是多少?
解:
提问:你能说说算数平均数与加权平均数的区别和
联系吗?
1.算数平均数是加权平均数的一种特殊情况(它特殊在各项的
权相等
2.在实际问题中,各项权不相等时,计算平均数时就要采用加权
平均数,当各项权相等时,计算平均数就要采用算数平均数。
练习2、疫情期间,某医院欲招聘医生,对甲、乙候选人进行了面视和笔试,他们的成绩如下表所示
(1)如果医院认为面试和笔试同等重要,从他们的成绩看,谁将被录取
候选人 测试成绩(百分制)
操作 笔试
甲 86 90
乙 92 83
(2)如果医院认为,作为医生操作的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取。
(2)如果医院认为,作为医生操作的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取。
(1)如果医院认为操作和笔试同等重要,从他们的成绩看,谁将被录取
在求n个数的平均数时,如果x1出现f1次,x2出现f2次,……xk出现fk次(这个f1+f2+……fk=n),那么这n个数的平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…fk分别叫做x1,x2,…,xk的权
2.加权平均数的其他形式
例2.新型冠状病毒肺炎发生以后,武汉成为疫情重灾区,医护人员数量告急,在党中央的统一领导下,全国上下积极支援,为了了解支援医护人员年龄情况,做了一次年龄调查,结果如下:33岁8人,34岁16人,35岁24人,36岁2人,求该支援医疗队的平均年龄(结果取整数)
解:这支支援医疗队的平均年龄为
(岁)
练习3.下表是校女子排球队员的年龄分布,求校女子排球队员的平均年龄。(结果取整数)
年龄/岁 13 14 15 16
频数 1 4 5 2
(岁)
解:
随堂练习
1.一组数据为10, 8, 9, 12, 13, 10, 8,则这组数据的
平均数是 .
2.已知一组数据4, 13, 24的权数分别是
则这组数据的加权平均数是 .
10
17
3.某公司有15名员工,他们所在的部门及相应每人所创造的年利润(万元)如下表:
部门 A B C D E F G
人数 1 1 2 2 2 2 5
利润 200 40 25 20 15 15 12
该公司每人所创造的年利润的平均数是 万元。
30
4.某次医术技能大赛,两名选手的成绩如下:
选手 测试成绩
创新 基本功 综合知识
A 72 85 67
B 85 74 70
(1)若按三项平均值取第一名,则 是第一名
B
(2)若三项测试得分按3:6:1的比例确定个人的测试成绩,此时第一名是谁呢?
解:
所以,此时第一名是A
权的常见形式有哪些?
1.比例(如2:1:3:4)
2.百分数(如50%、40% 、10%.)
3.频数(如8、16、24、2.)
课堂小结
一、两种平均数的求法:
算术平均数
加权平均数
加权平均数中的“权”的三种表现形式:
(1)频数 (2)百分比 (3)比例
二、“权”的意义:
表示数据的“重要程度”.
作业:
P113-练习1
P121-第1、4、5题
本节课结束
同学们,再见!
